Fig. 1. Scheme of a nerve cell.
The Project Gutenberg eBook of Giant brains; or Machines that think, by Edmund Callis Berkeley
Title: Giant brains; or Machines that think
Author: Edmund Callis Berkeley
Release Date: September 14, 2022 [eBook #68991]
Language: English
Produced by: Tim Lindell and the Online Distributed Proofreading Team at https://www.pgdp.net (This book was produced from images made available by the HathiTrust Digital Library.)
EDMUND CALLIS BERKELEY
Consultant in Modern Technology
President, E. C. Berkeley and Associates
JOHN WILEY & SONS, INC., NEW YORK
CHAPMAN & HALL, LIMITED, LONDON
Copyright, 1949
by
EDMUND CALLIS BERKELEY
All Rights Reserved
This book or any part thereof must not
be reproduced in any form without
the written permission of the publisher.
Second Printing, February, 1950
Printed in the United States of America
To my friends,
whose help and instruction
made this book possible
The subject of this book is a type of machine that comes closer to being a brain that thinks than any machine ever did before 1940. These new machines are called sometimes mechanical brains and sometimes sequence-controlled calculators and sometimes by other names. Essentially, though, they are machines that can handle information with great skill and great speed. And that power is very similar to the power of a brain.
These new machines are important. They do the work of hundreds of human beings for the wages of a dozen. They are powerful instruments for obtaining new knowledge. They apply in science, business, government, and other activities. They apply in reasoning and computing, and, the harder the problem, the more useful they are. Along with the release of atomic energy, they are one of the great achievements of the present century. No one can afford to be unaware of their significance.
In this book I have sought to tell a part of the story of these new machines that think. Perhaps you, as you start this book, may not agree with me that a machine can think: the first chapter of this book is devoted to the discussion of this question.
My purpose has been to tell enough about these machines so that we can see in general how they work. I have sought to explain some giant brains that have been built and to show how they do thinking operations. I have sought also to talk about what these machines can do in the future and to judge their significance for us. It seems to me that they will take a load off men’s as great as the load that printing took off men’s writing: a tremendous burden lifted.
We need to examine several of the new mechanical brains: Massachusetts Institute of Technology’s differential analyzer, Harvard’s IBM automatic sequence-controlled calculator, Moore School’s ENIAC [Pg viii] (Electronic Numerical Integrator and Calculator), and Bell Laboratories’ general-purpose relay calculator. These are described in the sequence in which they were finished between the years 1942 and 1946.
We also have to go on some excursions—for instance, the nature of language and of symbols, the meaning of thinking, the human brain and nervous system, the future design of machinery that can think, and a little algebra and logic. I have also sought to discuss the relations between machines that think and human society—what we can foresee as likely to happen or be needed as a result of the remarkable invention of machines that can think.
This book is intended for everyone. I have sought to put it together in such a way that any reader can select from it what he wants.
Perhaps at first reading you want only the main thread of the story. Then read only what seems interesting, and skip whatever seems uninteresting. The subheadings should help to tell you what to read and what to skip. Nearly all the chapters can be read with little reference to what goes before, although some reference to the supplements in the back may at times be useful.
Perhaps your memory of physics is dim, like mine. The little knowledge of physics needed is explained here and there throughout the book, and the index should tell where to find any explanation you may want.
Perhaps it is a long time since you did any algebra. Then Supplement 2 on mathematics may hold something of use to you. Two sections (one in Chapter 5 and one in Chapter 6) labeled as containing some rather mathematical details may be skipped with no great loss.
Perhaps you are unacquainted with logic that uses symbols—the branch of logic called mathematical logic. In fact, very few people are familiar with it. No discussion in the book hinges on understanding this subject, except for Chapter 9 where a machine that calculates logical truth is described. In all other chapters you may freely skip all references to mathematical logic. But, if you are curious about the [Pg ix] subject and how it can be usefully applied in the field of mechanical brains, then begin with the introduction to the subject in Chapter 9, and note the suggestions in the section entitled “Algebra of Logic” in Supplement 2.
In any case, glance at the table of contents, the chapter headings and subheadings, and the supplements at the back. These should give an idea of how the book is put together and how you may select what may be interesting to you.
Please do not read this book straight from beginning to end unless that way proves to be congenial to you. If you are not interested in technical details, skip most of the middle chapters, which describe existing mechanical brains. If, on the other hand, you want more details than this book contains, look up references in Supplement 3. Here are listed, with a few comments, over 250 books, articles, and pamphlets related to the subject of machinery for computing and reasoning. These cover many parts of the field; some parts, however, are not yet covered by any published information.
There are no photographs in this book, although there are over 80 drawings. Photographs of these complicated machines can really show very little: panels, lights, switches, wires, and other kinds of hardware. What is important is the way the machine works inside. This cannot be shown by a photograph but may be shown by schematic drawings. In the same way, a photograph of a human being shows almost nothing about how he thinks.
I have tried to write this book so that it could be understood. I have attempted to explain machinery for computing and reasoning without using technical words any more than necessary. To do this seemed to be easy in some places, much harder in others. As a test of this attempt, a count has been made of all the different words in the book that have two syllables or more, that are used for explaining, and that are not themselves defined. There are fewer than 1800 of these words. In Supplement 1, entitled “Words and Ideas,” I have digressed to discuss further the problem of explanation and understanding. [Pg x]
Every now and then in the book, along comes a word or a phrase that has a special meaning, for example, the name of something new. When it first appears, it is put in italics and is explained or defined. In addition, all the words and phrases having special meaning appear again in the index, and next to each is the page number of its explanation or definition.
In many places, I have talked of mechanical brains as if they were living. For example, instead of “capacity to store information” I have spoken of “memory.” Of course, the machines are not living; but they do have individuality, responsiveness, and other traits of living beings, just as a political party pictured as a living elephant does. Besides, to treat things as persons is a help in making any subject vivid and understandable, as every song writer and cartoonist illustrates. We speak of “Old Man River” and “Father Time”; we may speak of a ship or a locomotive as “she”; and the crew on the first Harvard sequence-controlled calculator has often called her “Bessy, the Bessel engine.”
Let us pause a little longer on the subject of understanding. What is the understanding of something new? It is a state of knowing, a process of knowing more and more. The more we know about something new, the better we understand it. It is possible for almost anybody to understand almost anything, I believe. What is mainly needed in order to grasp an idea is a good collection of true statements about it and some practice in using those statements in situations. For example, no one has ever seen or touched the separate scraps of electricity called electrons. But electrons have been described and measured; hundreds of thousands of people work with electrons; they know and use true statements about electrons. In effect, these people understand electrons.
Probably the hardest task of an author is to make his statements understandable yet accurate. It is too much to hope for complete success. I shall be very grateful to any reader who points out to me the statements that he has not understood or that are in error.
As to the views I have expressed, I do not expect every reader to agree with me. In fact, I shall be glad if many a reader disagrees with me. For then someone else may say to both of us, “You’re both right and [Pg xi] both wrong—the truth lies atwixt and atween you.” Thoughtful and tolerant disagreement is the finest climate for scientific progress.
Many of the mechanical brains described in this book will do good work for years; but their design is already out of date. Many organizations are hard at work finding new tricks in electronics, materials, and engineering and making new mechanical brains that are better and faster.
In spite of future developments, though, the basic facts about mechanical brains will endure. These basic facts are drawn from the principles of thinking, of mathematics, of science, of engineering, etc. These facts govern all handling of information. They do not depend very much on human or mechanical energy. They do not depend very much on signs. They do not depend very much on the century, or the language, or the country. For example, “II et III V sunt,” the Romans may have said; “deux et trois font cinq,” say the French; “2 + 3 = 5,” say the mathematicians; and we say, “two and three make five.” The main effort in this book has been to make clear the basic facts about mechanical brains, for they are now a masterly instrument for obtaining new knowledge.
New York 11, N. Y.
June 30, 1949
[Pg xii]
[Pg xiii]
This book has been over seven years in the making and has evolved through many different plans for its contents. It springs essentially from the desire to see human beings use their knowledge better: we know enough, but how are we to use what we know? Machines that handle information, that make knowledge accessible, are a long step in the direction of using what we know.
For help in causing this desire to come to fruition, I should like to express my indebtedness especially to Professor (then Commander, U.S.N.R.) Howard H. Aiken of Harvard University, whose stimulus, while I was stationed for ten months in 1945-46 in his laboratory, was very great.
I should also like to express my appreciation to Mr. Harry J. Volk, whose vision and enthusiasm greatly encouraged me in the writing of this book.
For careful reviews and helpful comments on the chapters dealing with existing mechanical brains, I am especially grateful to Dr. Franz L. Alt, Mr. E. G. Andrews, Professor Samuel H. Caldwell, Dr. Grace M. Hopper, Mr. Theodore A. Kalin, and Dr. John W. Mauchly, who are experts in their fields. Dr. Ruth P. Berkeley, Dr. Rudolf Flesch, Mr. J. Ross Macdonald, Dr. Z. I. Mosesson, Mr. Irving Rosenthal, Mr. Max S. Weinstein, and many others have been true friends in reading and commenting upon many parts of the manuscript. Mr. Frank W. Keller devoted much time and skill to converting my rough sketches into illustrations. Mr. Murray B. Ritterman has been of invaluable help in preparing and checking much of the bibliography. Miss Marjorie L. Black has helped very greatly in turning scraps of paper bearing sentences into an excellent manuscript for the printer.
For permission to use the quotations on various pages in Chapters 11 and 12, I am indebted to the kindness of: [Pg xiv]
E. P. Dutton & Co., for quotations from Frankenstein, by Mary W. Shelley, Everyman’s Library, No. 616.
Samuel French, for quotations from R. U. R., by Karel Čapek.[1]
Modern Industry, for a quotation from the issue of February 15, 1947.
Responsibility for the statements and opinions expressed in this book is solely my own. These statements and opinions do not necessarily represent the views of any organization with which I may be or have been associated. To the best of my knowledge and belief no information contained in this book is classified by the Department of Defense of the United States.
[Pg xv]
| 1. | CAN MACHINES THINK? | |
| What Is a Mechanical Brain? | 1 | |
| 2. | LANGUAGES: | |
| Systems for Handling Information | 10 | |
| 3. | A MACHINE THAT WILL THINK: | |
| The Design of a Very Simple Mechanical Brain | 22 | |
| 4. | COUNTING HOLES: | |
| Punch-Card Calculating Machines | 42 | |
| 5. | MEASURING: | |
| Massachusetts Institute of Technology’s | ||
| Differential Analyzer No. 2 | 65 | |
| 6. | ACCURACY TO 23 DIGITS: | |
| Harvard’s IBM Automatic | ||
| Sequence-Controlled Calculator | 89 | |
| 7. | SPEED—5000 ADDITIONS A SECOND: | |
| Moore School’s ENIAC | ||
| (Electronic Numerical Integrator and Calculator) | 113 | |
| 8. | RELIABILITY—NO WRONG RESULTS: | |
| Bell Laboratories’ | ||
| General-Purpose Relay Calculator | 128 | |
| 9. | REASONING: | |
| The Kalin-Burkhart Logical-Truth Calculator | 144 | |
| 10. | AN EXCURSION: | |
| The Future Design of Machines That Think | 167 | |
| 11. | THE FUTURE: | |
| Machines That Think, and | ||
| What They Might Do for Men | 180 | |
| 12. | SOCIAL CONTROL: | |
| Machines That Think, and | ||
| How Society May Control Them | 196 | |
| SUPPLEMENTS [Pg xvi] | ||
| 1. | Words and Ideas | 209 |
| 2. | Mathematics | 214 |
| 3. | References | 228 |
| INDEX | 257 | |
[Pg 1]
Recently there has been a good deal of news about strange giant machines that can handle information with vast speed and skill. They calculate and they reason. Some of them are cleverer than others—able to do more kinds of problems. Some are extremely fast: one of them does 5000 additions a second for hours or days, as may be needed. Where they apply, they find answers to problems much faster and more accurately than human beings can; and so they can solve problems that a man’s life is far too short to permit him to do. That is why they were built.
These machines are similar to what a brain would be if it were made of hardware and wire instead of flesh and nerves. It is therefore natural to call these machines mechanical brains. Also, since their powers are like those of a giant, we may call them giant brains.
Several giant mechanical brains are now at work finding out answers never before known. Two are in Cambridge, Mass.; one is at Massachusetts Institute of Technology, and one at Harvard University. Two are in Aberdeen, Md., at the Army’s Ballistic Research Laboratories. These four machines were finished in the period 1942 to 1946 and are described in later chapters of this book. More giant brains are being constructed.
Can we say that these machines really think? What do we mean by thinking, and how does the human brain think? [Pg 2]
We do not know very much about the physical process of thinking in the human brain. If you ask a scientist how flesh and blood in a human brain can think, he will talk to you a little about nerves and about electrical and chemical changes, but he will not be able to tell you very much about how we add 2 and 3 and make 5. What men know about the way in which a human brain thinks can be put down in a few pages, and what men do not know would fill many libraries.
Injuries to brains have shown some things of importance; for example, they have shown that certain parts of the brain have certain duties. There is a part of the brain, for instance, where sights are recorded and compared. If an accident damages the part of the brain where certain information is stored, the human being has to relearn—haltingly and badly—the information destroyed.
We know also that thinking in the human brain is done essentially by a process of storing information and then referring to it, by a process of learning and remembering. We know that there are no little wheels in the brain so that a wheel standing at 2 can be turned 3 more steps and the result of 5 read. Instead, you and I store the information that 2 and 3 are 5, and store it in such a way that we can give the answer when questioned. But we do not know the register in our brain where this particular piece of information is stored. Nor do we know how, when we are questioned, we are able automatically to pick up the nerve channels that lead into this register, get the answer, and report it.
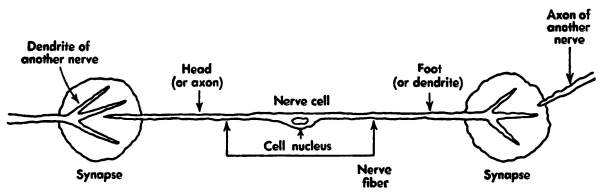
Since there are many nerves in the brain, about 10 billion of them, in fact, we are certain that the network of connecting nerves is a main part of the puzzle. We are therefore much interested in nerves and their properties.
A single nerve, or nerve cell, consists of a cell nucleus and a fiber. This fiber may have a length of anything from a [Pg 3] small fraction of an inch up to several feet. In the laboratory, successive impulses can be sent along a nerve fiber as often as 1000 a second. Impulses can travel along a nerve fiber in either direction at a rate from 3 feet to 300 feet a second. Because the speed of the impulse is far less than 186,000 miles a second—the speed of an electric current—the impulse in the nerve is thought by some investigators to be more chemical than electrical.
We know that a nerve cell has what is called an all-or-none response, like the trigger of a gun. If you stimulate the nerve up to a certain point, nothing will happen; if you reach that point, or cross it,—bang!—the nerve responds and sends out an impulse. The strength of the impulse, like the shot of the gun, has no relation whatever to the amount of the stimulation.

Fig. 1. Scheme of a nerve cell.
The structure between the end of one nerve and the beginning of the next is called a synapse (see Fig. 1). No one really knows very much about synapses, for they are extremely small and it is not easy to tell where a synapse stops and other stuff begins. Impulses travel through synapses in from ½ to 3 thousandths of a second. An impulse travels through a synapse only in one direction, from the head (or axon) of one nerve fiber to the foot (or dendrite) of another. It seems clear that the activity in a synapse is chemical. When the head of a nerve fiber brings in an impulse to a synapse, apparently a chemical called acetylcholine is released and may affect the foot of another fiber, thus transmitting the impulse; but the process and the conditions for it are still not well understood.
It is thought that nearly all information is handled in the brain by groups of nerves in parallel paths. For example, the eye is estimated [Pg 4] to have about 100 million nerves sensitive to light, and the information that they gather is reported by about 1 million nerves to the part of the brain that stores sights.
Not much more is yet known, however, about the operation of handling information in a human brain. We do not yet know how the nerves are connected so that we can do what we do. Probably the greatest obstacle to knowledge is that so far we cannot observe the detailed structure of a living human brain while it performs, without hurting or killing it.
Therefore, we cannot yet tell what thinking is by observing precisely how a human brain does it. Instead, we have to define thinking by describing the kind of behavior that we call thinking. Let us consider some examples.
When you and I add 12 and 8 and make 20, we are thinking. We use our minds and our understanding to count 8 places forward from 12, for example, and finish with 20. If we could find a dog or a horse that could add numbers and tell answers, we would certainly say that the animal could think.
With no trouble a machine can do this. An ordinary 10-column adding machine can be given two numbers like 1,378,917,766 and 2,355,799,867 and the instruction to add them. The machine will then give the answer, 3,734,717,633, much faster than a man. In fact, the mechanical brain at Harvard can add a number of 23 digits to another number of 23 digits and get the right answer in ³/₁₀ of a second.
Or, suppose that you are walking along a road and come to a fork. If you stop, read the signpost, and then choose left or right, you are thinking. You know beforehand where you want to go, you compare your destination with what the signpost says, and you decide on your route. This is an operation of logical choice.
A machine can do this. The mechanical brain now at Aberdeen which was built at Bell Laboratories can examine any number that comes up in the process of a calculation and tell whether it is bigger than 3 (or any stated number) or smaller. If the number is bigger than 3, the machine [Pg 5] will choose one process; if the number is smaller than 3, the machine will choose another process.
Now suppose that we consider the basic operation of all thinking: in the human brain it is called learning and remembering, and in a machine it is called storing information and then referring to it. For example, suppose you want to find 305 Main Street in Kalamazoo. You look up a map of Kalamazoo; the map is information kindly stored by other people for your use. When you study the map, notice the streets and the numbering, and then find where the house should be, you are thinking.
A machine can do this. In the Bell Laboratories’ mechanical brain, for example, the map could be stored as a long list of the blocks of the city and the streets and numbers that apply to each block. The machine will then hunt for the city block that contains 305 Main Street and report it when found.
A machine can handle information; it can calculate, conclude, and choose; it can perform reasonable operations with information. A machine, therefore, can think.
Now when we speak of a machine that thinks, or a mechanical brain, what do we mean? Essentially, a mechanical brain is a machine that handles information, transfers information automatically from one part of the machine to another, and has a flexible control over the sequence of its operations. No human being is needed around such a machine to pick up a physical piece of information produced in one part of the machine, personally move it to another part of the machine, and there put it in again. Nor is any human being needed to give the machine instructions from minute to minute. Instead, we can write out the whole program to solve a problem, translate the program into machine language, and put the program into the machine. Then we press the “start” button; the machine starts whirring; and it prints out the answers as it obtains them. Machines that handle information have existed for more than 2000 years. These two properties are new, however, and make a deep break with the past. [Pg 6]
How should we imagine a mechanical brain? One way to think of a mechanical brain is shown in Fig. 2. We see here a railroad line with four stations, marked input, storage, computer, and output. These stations are joined by little gates or switches to the main railroad line. We can imagine that numbers and other information move along this railroad line, loaded in freight cars. Input and output are stations where numbers or other information go in and come out, respectively. Storage is a station where there are many platforms and where information can be stored. The computer is a special station somewhat like a factory; when two numbers are loaded on platforms 1 and 2 of this station and an order is loaded on platform 3, then another number is produced on platform 4.
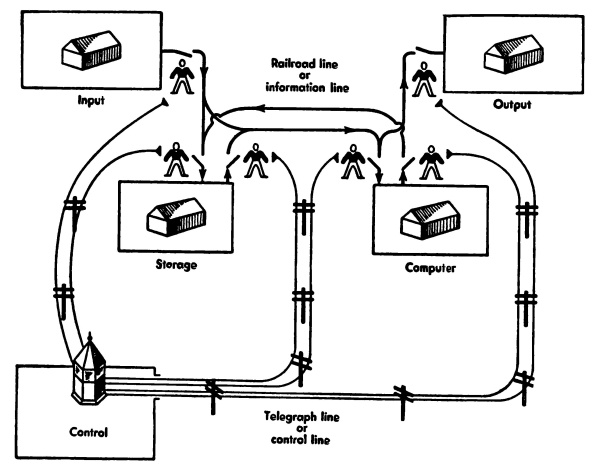
Fig. 2. Scheme of a mechanical brain.
We see also a tower, marked control. This tower runs a telegraph line to each of its little watchmen standing by the gates. The tower tells them when to open and when to shut which gates.
Now we can see that, just as soon as the right gates are shut, freight [Pg 7] cars of information can move between stations. Actually the freight cars move at the speed of electric current, thousands of miles a second. So, by closing the right gates each fraction of a second, we can flash numbers and information through the system and perform operations of reasoning. Thus we obtain a mechanical brain.
In general, a mechanical brain is made up of:
1. A quantity of registers where information (numbers and instructions) can be stored.
2. Channels along which information can be sent.
3. Mechanisms that can carry out arithmetical and logical operations.
4. A control, which guides the machine to perform a sequence of operations.
5. Input and output devices, whereby information can go into the machine and come out of it.
6. Motors or electricity, which provide energy.
There are many kinds of thinking that mechanical brains can do. Among other things, they can:
They do these things much better than you or I. They are fast. The mechanical brain built at the Moore School of Electrical Engineering at the University of Pennsylvania does 5000 additions a second. They are reliable. Even with hundreds of thousands of parts, the existing giant [Pg 8] brains have worked successfully. They have remarkably few mechanical troubles; in fact, for one of the giant brains, a mechanical failure is of the order of once a month. They are powerful. The big machine at Harvard can remember 72 numbers each of 23 digits at one time and can do 3 operations with these numbers every second. The mechanical brains that have been finished are able to solve problems that have baffled men for many, many years, and they think in ways never open to men before. Mechanical brains have removed the limits on complexity of routine: the machine can carry out a complicated routine as easily as a simple one. Already, processes for solving problems are being worked out so that the mechanical brain will itself determine more than 99 per cent of all the routine orders that it is to carry out.
But, you may ask, can they do any kind of thinking? The answer is no. No mechanical brain so far built can:
A clever wild animal, for example, a fox, can do all these things; a mechanical brain, not yet. There is, however, good reason to believe that most, if not all, of these operations will in the future be performed not only by animals but also by machines. Men have only just begun to construct mechanical brains. All those finished are children; they have all been born since 1940. Soon there will be much more remarkable giant brains.
Most of the thinking so far done by these machines is with numbers. They have already solved problems in airplane design, astronomy, physics, mathematics, engineering, and many other sciences, that previously could not be solved. To find the solutions of these problems, mathematicians would have had to work for years and years, using the best known methods and large staffs of human computers. [Pg 9]
These mechanical brains not only calculate, however. They also remember and reason, and thus they promise to solve some very important human problems. For example, one of these problems is the application of what mankind knows. It takes too long to find understandable information on a subject. The libraries are full of books: most of them we can never hope to read in our lifetime. The technical journals are full of condensed scientific information: they can hardly be understood by you and me. There is a big gap between somebody’s knowing something and employment of that knowledge by you or me when we need it. But these new mechanical brains handle information very swiftly. In a few years machines will probably be made that will know what is in libraries and that will tell very swiftly where to find certain information. Thus we can see that mechanical brains are one of the great new tools for finding out what we do not know and applying what we do know.
[Pg 10]
As everyone knows, it is not always easy to think. By thinking, we mean computing, reasoning, and other handling of information. By information we mean collections of ideas—physically, collections of marks that have meaning. By handling information, we mean proceeding logically from some ideas to other ideas—physically, changing from some marks to other marks in ways that have meaning. For example, one of your hands can express an idea: it can store the number 3 for a short while by turning 3 fingers up and 2 down. In the same way, a machine can express an idea: it can store information by arranging some equipment. The Harvard mechanical brain can store 132 numbers between 0 and 99,999,999,999,999,999,999,999 for days. When you want to change the number stored by your fingers, you move them: perhaps you need a half second to change the number stored by your fingers from 3 to 2, for example. In the same way, a machine can change a stored number by changing the arrangement of some equipment: the electronic brain Eniac can change a stored number in ¹/₅₀₀₀ of a second.
Since it is not always easy to think, men have given much attention to devices for making thinking easier. They have worked out many systems for handling information, which we often call languages. Some languages are very complete and versatile and of [Pg 11] great importance. Others cover only a narrow field—such as numbers alone—but in this field they may be remarkably efficient. Just what is a language?
Every language is both a scheme for expressing meanings and physical equipment that can be handled. For example, let us take spoken English. The scheme of spoken English consists of more than 150,000 words expressing meanings, and some rules for putting words together meaningfully. The physical equipment of spoken English consists of (1) sounds in the air, and (2) the ears of millions of people, and their mouths and voices, by which they can hear and speak the sounds of English. For another example, let us take numbers expressed in the Arabic numerals and the rules of arithmetic. The scheme of this language contains only ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 or their equivalents, and some rules for combining them. Sufficient physical equipment for this language might very well be a ten-column desk calculating machine with its counter wheels, gears, keys, etc. If we tried to exchange the physical equipment of these two languages, we would be blocked: the desk calculating machine cannot possibly express the meaningful combinations of 150,000 words, and sounds in the air are not permanent enough to express the steps of division of one large number by another.
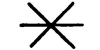
If we examine languages that have existed, we can observe a number of schemes for expressing meanings. In the table on pp. 12-13 is a rough list of a dozen of them. From among these we can choose the schemes that are likely to be useful in mechanical brains. Schemes 11 and 12 are the schemes that have been predominantly used in machinery for computing. Scheme 12 consisting of combinations of just two marks, ✓, ✕, provides one of the best codes for mechanical handling of information. This scheme, called binary coding (see Supplement 2), is also useful for measuring the quantity of information.
How should we measure the quantity of information? The smallest unit of information is a “yes” or a “no,” a check mark (✓) or a cross (✕), an impulse in a nerve or no impulse, a 1 or a 0, black or white, good or bad, etc. This twofold difference is called a binary digit of information (see Supplement 2). It is the convenient unit of information. [Pg 12]
SCHEMES FOR EXPRESSING MEANINGS
| Example: | |||||
|---|---|---|---|---|---|
| /——————^—————————\ | |||||
| No. | Principle of Scheme |
Sign | Used in | Significance | Name of Scheme |
| (1) | (2) | (3) | (4) | (5) | (6) |
| Sounds | |||||
| 1. | Sound of new word is like sound of referent |
Bobwhite[2] | Spoken English |
kind of quail, so called from its note |
Imitative; bowwow theory |
| 2. | An utterance becomes a new word |
Pooh![3] | Spoken English |
The speaker expresses disdain |
Pooh-pooh theory |
| 3. | New word is like another word |
Chortle[4] | Spoken English; invented by Lewis Carroll, 1896 |
“Chuckle” and “snort” blended |
Analogical |
| 4. | Word has been used through the ages |
Mother[5] | Spoken English |
Female parent |
Historical |
| Sights | |||||
| 5. | Picture is like referent |
 |
Egyptian; Ojibwa (American Indian) |
Picture of eye and tears, to mean grief |
Imitative; pictographic |
| 6.[Pg 13] | Pattern is symbol of an idea |
5 | English; French; German; etc. |
Five; cinq; fünf; etc. |
Ideographic; mathematical; symbolic; numeric |
| Mapping of Sounds | |||||
| 7. | Object pictured as the wanted sound |
 |
Possible English |
Picture of a knot to mean “not” |
Rebus- writing; phonographic |
| 8. | Pattern is symbol for a large ound unit |
 |
Ancient Cypriote (island of Cyprus) |
Sign for the syllable mu |
Syllable- writing |
| 9. | Pattern is symbol for a small sound unit |
Ʒ | International Phonetic Alphabet of 87 characters |
The sound zh, as s in “measure” |
Phonetic writing alphabetic writing; |
| Mapping of Sights or Symbols | |||||
| 10. | Systematic combinations of 26 letters |
ENIAC | Abbreviations, etc. |
Initial letters of a 5-word title |
Alphabetic coding |
| 11. | Systematic combinations of 10 digits |
135-03-1228 | Abbreviations, nomenclature, etc. |
Social Security No. of a person |
Numeric coding |
| 12. | Systematic combinations of 2 marks |
✓,✕,✕,✓,✓ | Checking lists, etc. |
“yes,” “no,” “no,” “yes,” “yes,” respectively |
Binary coding |
[Pg 14] With 2 units of information or 2 binary digits (1 or 0) we can represent 4 pieces of information:
00, 01, 10, 11
With 3 units of information we can represent 8 pieces of information:
000, 001, 010, 011, 100, 101, 110, 111
With 4 units of information we can represent 16 pieces of information:
| 0000 | 0001 | 0010 | 0011 |
| 0100 | 0101 | 0110 | 0111 |
| 1000 | 1001 | 1010 | 1011 |
| 1100 | 1101 | 1110 | 1111 |
Now 4 units of information are sufficient to represent a decimal digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and allow 6 possibilities to be left over; 3 units of information are not sufficient. For example, we may have:
| 0 | 0000 | 5 | 0101 |
| 1 | 0001 | 6 | 0110 |
| 2 | 0010 | 7 | 0111 |
| 3 | 0011 | 8 | 1000 |
| 4 | 0100 | 9 | 1001 |
We say, therefore, that a decimal digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 is equivalent to 4 units of information. Thus a table containing 10,000 numbers, each of 10 decimal digits, is equivalent to 400,000 units of information.
One of the 26 letters of the alphabet is equivalent to 5 units of information, for, 5 binary digits (1 or 0) have 32 possible arrangements, and these are enough to provide for the 26 letters. Any printed information in English can be expressed in about 80 characters consisting of 10 numerals, 52 capital and small letters, and some 18 punctuation marks and other types of marks; 6 binary digits (1 or 0) have 64 possible arrangements, and 7 binary digits (1 or 0) have 128 [Pg 15] possible arrangements. Each character in a printed book, therefore, is roughly equivalent to 7 units of information.
It can be determined that a big telephone book or a big reference dictionary stores printed information at the rate of about 1 billion units of information per cubic foot. If the 10 billion nerves in the human brain could independently be impulsed or not impulsed, then the human brain could conceivably store 10 billion units of information. The largest library in the world is the Library of Congress, containing 7 million volumes including pamphlets. It stores about 100 trillion units of information.
We can thus see the significance of a quantity of information from 1 unit to 100 trillion units. No distinction is here made between information that reports facts and information that does not. For example, a book of fiction about persons who never existed is still counted as information, and, of course, much instruction and entertainment may be found in such a source.
The first thing we want to do with information is store it. The second thing we want to do is combine it. We want equipment that makes these two processes easy and efficient. We want equipment for handling information that:
1. Costs little.
2. Holds much information in little space.
3. Is permanent, when we want to keep the information.
4. Is erasable, when we want to remove information.
5. Is versatile, holds easily any kind of information, and allows operations to be done easily.
The amount of human effort needed to handle information correctly depends very much on the properties of the physical equipment expressing the information, although the laws of correct reasoning are independent of the equipment. For example, the great difficulty with spoken sounds as physical equipment for handling information is the trouble of storing them. The technique for doing so was mastered only about 1877 when Thomas A. Edison made the first phonograph. Even with this advance, no one can glance at a soundtrack and tell quickly what sounds are stored there; only by turning back the machine and listening to a groove can we determine this. It was not possible for the men of 2000 b.c. to wait thousands of years for the storing of spoken sounds. The problem of storing information was accordingly taken to other types of physical equipment. [Pg 16]
PHYSICAL EQUIPMENT FOR
HANDLING INFORMATION
| No. | Physical Objects |
Arranged in or on |
Operated or Produced by |
Low Cost? |
Little Space? |
Perma- nent? |
Eras- able? |
Vers- atile? |
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| Mind | ||||||||
| 1. | Nerve cells |
Human brain |
Body | ✕ | ✓✓ | ✓ | ✓ | ✓✓ |
| Sounds | ||||||||
| 2. | Sounds | Air | Voice | ✓✓ | ✓✓ | ✕✕ | ✓✓ | ✓✓ |
| 3. | Sound- tracks |
Wax cylinders, phonograph records |
Machines and motors |
✓ | ✓ | ✓✓ | ✕ | ✓✓ |
| Sights | ||||||||
| 4. | Marks | Sand | Stick | ✓ | ✕ | ✓ | ✓✓ | ✕ |
| 5. | Colored painting canvases, etc. |
Cave walls, |
Paintbrush and paints |
✕ | ✕ | ✓ | ✕ | ✕✕ |
| 6. | Marks, inscript- ions |
Clay, stone |
Stylus, chisel |
✕✕ | ✓ | ✓✓ | ✕✕ | ✓ |
| 7. | Marks | Slate | Chalk | ✓ | ✕ | ✓ | ✓✓ | ✓ |
| 8. | Marks parchment, etc. |
Paper, and ink, pencil |
Pen | ✓✓ | ✓ | ✓ | ✕ | ✓✓ |
| 9. | Letters, etc. |
Paper books etc. |
Printing press, movable type, motor, and hands |
✓✓ | ✓✓ | ✓✓ | ✕✕ | ✓✓ |
| 10. | Photo- graphs |
Film, prints, etc. |
Camera | ✓ | ✓✓ | ✓ | ✕✕ | ✓✓ |
| 11. | Letters, etc. |
Paper, mimeograph stencil, etc. |
Typewriter and fingers |
✓ | ✓✓ | ✓ | ✕ | ✓✓ |
| Body [Pg 17] | ||||||||
| 12. | Gestures | Space | Body | ✓ | ✕ | ✕✕ | ✓✓ | ✕✕ |
| 13. | Fingers | Hands | Body | ✕ | ✕ | ✕✕ | ✓✓ | ✕✕ |
| Objects | ||||||||
| 14. | Pebbles | Slab | Hands | ✓✓ | ✓ | ✓ | ✓ | ✕✕ |
| 15. | Knots | String | Hands | ✓✓ | ✓ | ✓ | ✓ | ✕✕ |
| 16. | Tallies, notches |
Stick | Knife | ✓✓ | ✓ | ✓✓ | ✕✕ | ✕✕ |
| 17. | Beads | Rods in a frame, abacus |
Hands | ✓ | ✓ | ✓ | ✓✓ | ✕✕ |
| 18. | Ruled lines, pointers |
Rulers, scales, dials |
Hands, pressure, etc. |
✓ | ✓ | ✓ | ✓ | ✓ |
| Machines | ||||||||
| 19. | Counter wheels, gears, keys, lights, etc. |
Desk calculating machines, fire-control instruments, etc. |
Motor and hands |
✓ | ✓ | ✓ | ✓✓ | ✓ |
| 20. | Punched cards and paper tape |
Punch card machinery, teletype, etc. |
Motor and input instructions |
✓✓ | ✓✓ | ✓ | ✕ | ✓✓ |
| 21. | Relays | Dial telephone, other machinery |
Motor and input instructions |
✕ | ✓ | ✓ | ✓✓ | ✓✓ |
| 22. | Elect- ronic tubes |
Machinery | Motor and input instructions |
✓ | ✓ | ✓ | ✓✓ | ✓✓ |
| 23. | Magnetic surfaces: wire, tape, discs |
Machinery | Motor and input instructions |
✓✓ | ✓✓ | ✓✓ | ✓✓ | ✓✓ |
| 24. | Delay lines: electric, acoustic |
Machinery | Motor and input instructions |
✕ | ✓ | ✕ | ✓✓ | ✓✓ |
| 25. | Electro- static storage tubes |
Machinery | Motor and input instructions |
✕ | ✓✓ | ✕ | ✓✓ | ✓✓ |
[Pg 18] What are the types of physical equipment for handling information, and which are the good ones? In the table on pp. 16-17 is a rough list of 25 types of physical equipment for handling information. ✓✓ means “yes, very;” ✓ means “yes, adequately;” ✕ means “not generally;” ✕✕ means “not at all.”
For example, our fingers (see No. 13) as a device for handling information are very expensive for most cases. They take up a good deal of space. Certainly they are very temporary storage; any information they may express is very erasable; and what we can express with them alone is very limited. Yet, with a typewriter (see No. 11), our fingers become versatile and efficient. In fact, our fingers can make 4 strokes a second; we can select any one of about 38 keys; and, since each key is equivalent to 5 or 6 units of information, the effective speed of our fingers may be about 800 units of information a second.
The use of pebbles (see No. 14) for keeping track of numerical information is shown in the history of the words containing the root calc-of the word calculate. The Latin word calcis meant pertaining to lime or limestone, and the Latin word calculus derived from it meant first a small piece of limestone, and later any small stone, particularly a pebble used in counting. All three of these meanings have left descendants: “chalk,” “calcite,” “calcium,” relating in one way or another to lime; in medicine, “calculus,” referring to stones in the kidneys or elsewhere in the body; and in mathematics, “calculate,” “calculus,” referring to computations, once done with pebbles.
The pebbles, and the slab (for which the ancient Greek word is abax) on which they were arranged and counted, were later replaced, for ease in handling, by groups of beads strung on rods and [Pg 19] placed in a frame (see No. 17). These constituted the abacus (see Supplement 2 and the figure there). This was the first calculating machine. It is still used all over Asia; in fact, even today more people use the abacus for accounting than use pencil and paper. The skill with which the abacus can be used was shown in November 1946 in a well-publicized contest in Japan. Kiyoshi Mastuzaki, a clerk in the Japanese communications department, using the abacus, challenged Private Thomas Wood of the U. S. Army, using a modern desk calculating machine, and defeated him in a speed contest involving additions, subtractions, multiplications, and divisions.
The heaps of small pebbles, the notches in sticks, and the abacus had the advantage of being visible and comparatively permanent. Storing and reading were relatively easy. They were rather compact and easy to manipulate, certainly much easier than spoken words. But they were subject to disadvantages also. Moving correctly from one arrangement to another was difficult, since there was no good way for storing intermediate steps so that the process could be easily verified. Furthermore, these devices applied to specified numbers only. Also, there was no natural provision for recording what the several numbers belonged to. This had to be recorded with the help of another language, writing.
The language of physical objects was picked up from obscurity by the invention of motors and the demands of commerce and business. Commencing in the late 1800’s, desk calculating machines (see No. 19) were constructed to meet mass calculation requirements. They would add, subtract, multiply, and divide specific numbers with great accuracy and speed. But until recently they still were adjuncts to the other languages, for they provided figures one at a time for insertion in the spaces on the ledger pages or calculation sheets where figures were called for.
Beginning in the 1920’s, a remarkable change has taken place. Instead of performing single operations, machines have been developed to perform chains of operations with many kinds of information. One of these machines is the dial telephone: it can select one of 7 million telephones by successive sorting according to the letters and digits of a telephone number. Another of these machines is a [Pg 20] fire-control instrument, a mechanism for controlling the firing of a gun. For example, in a modern anti-aircraft gun the mechanism will observe an enemy plane flying at several hundred miles an hour, convert the observations into gun-aiming directions, and determine the aiming directions fast enough to shoot down the plane. Punch-card machinery, machines handling information expressed as punched holes in cards, enable the fulfillment of social security legislation, the production of the census, and countless operations of banks, insurance companies, department stores, and factories. And, finally, in 1942 the first mechanical brain was finished at Massachusetts Institute of Technology.
Let us consider the two modern physical devices for handling information which make mechanical brains possible. These are relays and electronic tubes (Nos. 21 and 22). The last three kinds of equipment listed in the table (magnetic surfaces, No. 23; delay lines, No. 24; and electrostatic storage tubes, No. 25) were not included in any mechanical brains functioning by the middle of 1948. The discussion of them is therefore put off to Chapter 10, where we talk about the future design of mechanical brains.

Fig. 1. Relay
[Pg 21] Figure 1 shows a simple relay. There are two electrical circuits here. One has two terminals—Pickup and Ground. The other has three terminals—Common, Normally Open, and Normally Closed. When current flows through the coil of wire around the iron, it makes the iron a magnet; the magnet pulls down the flap of iron above, overcoming the force of the spring. When there is no current through the coil, the iron is not a magnet, and the flap is held up by the spring. Now suppose that there is current in Common. When there is no current in Pickup, the current from Common will flow through the upper contact, to the terminal marked Normally Closed. When there is current in Pickup, the current from Common will flow through the lower contact, to the terminal marked Normally Open. Thus we see that a relay expresses a “yes” or a “no,” a 1 or 0, a binary digit, a unit of information. A relay costs $5 to $10. It is rather expensive for storing a single unit of information. The fastest it can be changed from 1 to 0, or vice versa, is about ¹/₁₀₀ of a second.

Fig. 2. Electronic tube.
Figure 2 shows a simple electronic tube. It has three parts—the Cathode, the Grid, and the Plate. The Grid actually is a coarse net of metal wires. Electrons can flow from the Cathode to the Plate, provided the voltage on the Grid is such as to permit them to flow. So we can see that an electronic tube is a very simple on-off device and expresses a “yes” or a “no,” a 1 or 0, a binary digit, a unit of information. A simple electronic tube suitable for calculating purposes costs 50 cents to a $1, only ⅒ the cost of a relay. It can be changed from 1 to 0, or back again, in 1 millionth of a second.
Relays have been widely used in the mechanical brains so far built, and electronic tubes are the essence of Eniac.
In the next chapter, we shall see how physical equipment for handling information can be put together to make a simple mechanical brain.
[Pg 22]
We shall now consider how we can design a very simple machine that will think. Let us call it Simon, because of its predecessor, Simple Simon.
By designing Simon, we shall see how we can put together physical equipment for handling information in such a way as to get a very simple mechanical brain. At every point in the design of Simon, we shall make the simplest possible choice that will still give us a machine that: handles information, transfers information automatically from one part of the machine to another, and has control over the sequence of operations. Simon is so simple and so small, in fact, that it could be built to fill up less space than a grocery-store box, about 4 cubic feet. If we know a little about electrical work, we will find it rather easy to make Simon.
What do we do first to design the very simple mechanical brain, Simon?
The first thing we have to decide about Simon is how information will be represented: as we put it into Simon, as it is moved around inside [Pg 23] of Simon, and as it comes out of Simon. We need to decide what physical equipment we shall use to make Simon’s flesh and nerves. Since we are taking the simplest convenient solution to each problem, let us decide to use: punched paper tape for putting information in, relays (see Chapter 2) and wires for storing and transferring information, and lights for putting information out.

Fig. 1. Simon, the very simple mechanical brain.
For the equipment inside Simon, we could choose either electronic tubes or relays. We choose relays, although they are slower, because it is easier to explain circuits using relays. We can look at a relay circuit laid out on paper and tell how it works, just by seeing whether or not current will flow. Examples will be given below. When we look at a circuit using electronic tubes laid out on paper, we still need to know a good deal in order to calculate just how it will work.
How will Simon perceive a number or other information by means of punched tape, or relays, or lights? With punched paper tape having, for example, 2 spaces where holes may be, Simon can be told 4 numbers—00, 01, 10, 11. Here the binary digit 1 means a hole punched; the binary digit 0 means no hole punched. With 2 relays together in a register, Simon can remember any one of the 4 numbers 00, 01, 10, and 11. Here the binary digit 1 means the relay picked up or energized or closed; 0 means the relay not picked up or not energized or open. With 2 lights, Simon can give as an answer any one of the 4 numbers 00, 01, 10, 11. In this case the binary digit 1 means the light glowing; 0 means the light off. (See Fig. 1.) [Pg 24]
We can say that the two lights by which Simon puts out the answer are his eyes and say that he tells his answer by winking. We can say also that the two mechanisms for reading punched paper tape are Simon’s ears. One tape, called the input tape, takes in numbers or operations. The other tape takes in instructions and is called the program tape.
We can say that Simon has a mentality of 4. We mean not age 4 but just the simple fact that Simon knows only 4 numbers and can do only 4 operations with them. But Simon can keep on doing these operations in all sorts of routines as long as Simon has instructions. We decide that Simon will know just 4 numbers, 0, 1, 2, 3, in order to keep our model mechanical brain very simple. Then, for any register, we need only 2 relays; for any answer, we need only 2 lights.
Any calculating machine has a mentality, consisting of the whole collection of different ideas that the machine can ever actually express in one way or another. For example, a 10-place desk calculating machine can handle numbers up to 10 decimal digits without additional capacity. It cannot handle bigger numbers.
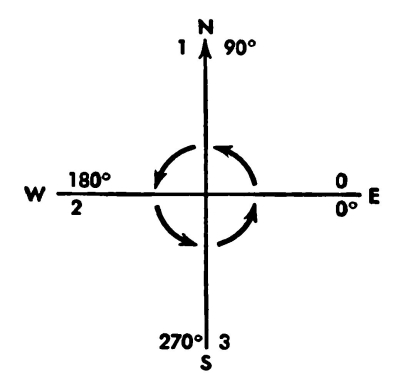
Fig. 2. Four directions.
What are the 4 operations with numbers which Simon can carry out? Let us consider some simple operations that we can perform with just 4 numbers. Suppose that they stood for 4 directions in the order east, north, west, south (see Fig. 2). Or suppose that they stood for a turn counterclockwise through some right angles as follows:
Then we could have the operations of addition and negation, defined as follows: [Pg 25]
| Addition | Negation | |||||||
|---|---|---|---|---|---|---|---|---|
| c = a + b | c = -a | |||||||
| b: | 0 | 1 | 2 | 3 | ||||
| a: | a | c | ||||||
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | ||
| 1 | 1 | 2 | 3 | 0 | 1 | 3 | ||
| 2 | 2 | 3 | 0 | 1 | 2 | 2 | ||
| 3 | 3 | 0 | 1 | 2 | 3 | 1 | ||
For example, the first table says, “1 plus 3 equals 0.” This means that, if we turn 1 right angle and then turn in the same direction 3 more right angles, we face in exactly the same way as we did at the start. This statement is clearly true. For another example, the second table says, “2 is the negative of 2.” This means that, if we turn to the left 2 right angles, we face in exactly the same way as if we turn to the right 2 right angles, and this statement also is, of course, true.
With only these two operations in Simon, we should probably find him a little too dull to tell us much. Let us, therefore, put into Simon two more operations. Let us choose two operations involving both numbers and logic: in particular, (1) finding which of two numbers is greater and (2) selecting. In this way we shall make Simon a little cleverer.
It is easy to teach Simon how to find which of two numbers is the greater when all the numbers that Simon has to know are 0, 1, 2, 3. We put all possible cases of two numbers a and b into a table:
| b: | 0 | 1 | 2 | 3 | ||||
| a: | ||||||||
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
Then we tell Simon that we shall mark with 1 the cases where a is greater than b and mark with 0 the cases where a is not greater than b:
| Greater Than | |||||
|---|---|---|---|---|---|
| b: | 0 | 1 | 2 | 3 | |
| a: | |||||
| 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | |
| 2 | 1 | 1 | 0 | 0 | |
| 3 | 1 | 1 | 1 | 0 | |
[Pg 26] For example, “2 is greater than 3” is false, so we put 0 in the table on the 2 line in the 3 column. We see that, for the 16 possible cases, a is greater than b in 6 cases and a is not greater than b in 10 cases.
There is a neat way of saying what we have just said, using the language of mathematical logic (see Chapter 9 and Supplement 2). Suppose that we consider the statement “a is greater than b” where a and b may be any of the numbers 0, 1, 2, 3. We can say that the truth value p of a statement P is 1 if the statement is true and that it is 0 if the statement is false:
p = 1 if P is true, 0 if P is false
The truth value of a statement P is conveniently denoted as T(P) (see Supplement 2):
p = T(P)
Now we can say that the table for the operation greater than shows the truth value of the statement “a is greater than b”:
p = T(a > b)
Let us turn now to the operation selection. By selecting we mean choosing one number a if some statement P is true and choosing another number b if that statement is not true. As before, let p be the truth value of that statement P, and let it be equal to 1 if P is true and to 0 if P is false. Then the operation of selection is fully expressed in the following table and logical formula (see Supplement 2):
| Selection | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| c = a·p + b·(1 - p) | |||||||||
| p: | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| b: | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | |
| a: | |||||||||
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | |
| 2 | 0 | 1 | 2 | 3 | 2 | 2 | 2 | 2 | |
| 3 | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 3 | |
For example, suppose that a is 2 and b is 3 and the statement P is the statement “2 is greater than 0.” Since this statement is true, p is 1, and
a·p + b·(1 - p) = 2(1) + 3(0) = 2
[Pg 27] This result is the same as selecting 2 if 2 is greater than 0 and selecting 3 if 2 is not greater than 0.
Thus we have four operations for Simon that do not overstrain his mentality; that is, they do not require him to go to any numbers other than 0, 1, 2, and 3. These four operations are: addition, negation, greater than, selection. We label these operations also with the numbers 00 to 11 as follows: addition, 00; negation, 01; greater than, 10; selection, 11.
The memory of a mechanical brain consists of physical equipment in which information can be stored. Usually, each section of the physical equipment which can store one piece of information is called a register. Each register in Simon will consist of 2 relays. Each register will hold any of 00, 01, 10, 11. The information stored in a register 00, 01, 10, 11 may express a number or may express an operation.
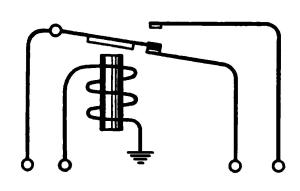
S1-2
Relay energized
S1-1
Relay not energized
Fig. 3. Register S1 storing 10.
How many registers will we need to put into Simon to store information? We shall need one register to read the input tape and to store the number or operation recorded on it. We shall call this register the input register I. We shall need another register to store the number or operation that Simon says is the answer and to give it to the output lights. We shall call this register the output register O. We shall need 5 registers for the part of Simon which does the computing, which we shall call the computer: we shall need 3 to store numbers put into the computer (C1, C2, C3), 1 to store the operation governing the computer (C4), and 1 to [Pg 28] store the result (C5). Suppose that we decide to have 8 registers for storing information, so as to provide some flexibility for doing problems. We shall call these registers storage registers and name them S1, S2, S3, ··· S8. Then Simon will have 15 registers: a memory that at one time can hold 15 pieces of information.
How will one of these registers hold information? For example, how will register S1 hold the number 2 (see Fig. 3)? The number 2 in machine language is 10. Register S1 consists of two relays, S1-2 and S1-1. 10 stored in register S1 means that relay S1-2 will be energized and that relay S1-1 will not be energized.
So far we have said nothing about the control of Simon. Is he docile? Is he stubborn? We know what his capacity is, but we do not know how to tell him to do anything. How do we connect our desires to his behavior? How do we tell him a problem? How do we get him to solve it and tell us the answer? How do we arrange control over the sequence of his operations? For example, how do we get Simon to add 1 and 2 and tell us the answer 3?
On the outside of Simon, we have said, there are two ears: little mechanisms for reading punched paper tape. Also there are two eyes that can wink: light bulbs that by shining or not shining can put out information (see Fig. 1). One of the ears—let us call it the left ear—takes in information about a particular problem: numbers and operations. Here the problem tape or input tape is listened to. Each line on the input tape contains space for 2 punched holes. So, the information on the input tape may be 00, 01, 10, or 11—either a number or an operation. The other ear—let us call it the right ear—takes in information about the sequence of operations, the program or routine to be followed. Here the program tape or routine tape or control tape is listened to. Each line on the program tape contains space for 4 punched holes. We tell Simon by instructions on the program tape what he is to do with the information that we give him on the input tape. The [Pg 29] information on the program tape, therefore, may be 0000, 0001, 0010, ···, 1111, or any number from 0 to 15 expressed in binary notation (see Supplement 2).
How is this accomplished? In the first place, Simon is a machine, and he behaves during time. He does different things from time to time. His behavior is organized in cycles. He repeats a cycle of behavior every second or so. In each cycle of Simon, he listens to or reads the input tape once and he listens to or reads the program tape twice. Every complete instruction that goes on the program tape tells Simon a register from which information is to be sent and a register in which information is to be received. The first time that he reads the program tape he gets the name of the register that is to receive certain information, the receiving register. The second time he reads the program tape he gets the name of the register from which information is to be sent, the sending register. He finishes each cycle of behavior by transferring information from the sending register to the receiving register.
For example, suppose that we want to get an answer out of Simon’s computer into Simon’s output lights. We put down the instruction
Send information from C5 into O
or, more briefly,
C5 → O
But he does not understand this language. We must translate into machine language, in this case punched holes in the program tape. Naturally, the punched holes in the program tape must be able to specify any sending register and any receiving register. There are 15 registers, and so we give them punched hole codes as follows:
| Register | Code | Register | Code |
|---|---|---|---|
| I | 0001 | C1 | 1010 |
| S1 | 0010 | C2 | 1011 |
| S2 | 0011 | C3 | 1100 |
| S3 | 0100 | C4 | 1101 |
| S4 | 0101 | C5 | 1110 |
| S5 | 0110 | O | 1111 |
| S6 | 0111 | ||
| S7 | 1000 | ||
| S8 | 1001 | ||
[Pg 30] To translate the direction of transfer of information, which we showed as an arrow, we put on the program tape the code for the receiving register first—in this case, output, O, 1111—and the code for the sending register second—in this case, C5, 1110. The instruction becomes 1111, 1110. The first time in any cycle that Simon listens with his right ear, he knows that what he hears is the name of the receiving register; and the second time that he listens, he knows that what he hears is the name of the sending register. One reason for this sequence is that any person or machine has to be prepared beforehand to absorb or take in any information.
Now how do we tell Simon to add 1 and 2? On the input tape, we put:
| Add | 00 |
| 1 | 01 |
| 2 | 10 |
On the program tape, we need to put:
I → C4
I → C1
I → C2
C5 → O
which becomes:
1101, 0001;
1010, 0001;
1011, 0001;
1111, 1110
Thus we can see that Simon can do such a problem as:
Add 0 and 3.
Add 2 and the negative of 1.
Find which result is greater.
Select 3 if this result equals 2;
otherwise select 2.
To work out the coding for this and like problems would be a good exercise. Simon, in fact, is a rather clever little mechanical brain, even if he has only a mentality of 4. [Pg 31]
It may seem that a simple model of a mechanical brain like Simon is of no great practical use. On the contrary, Simon has the same use in instruction as a set of simple chemical experiments has: to stimulate thinking and understanding and to produce training and skill. A training course on mechanical brains could very well include the construction of a simple model mechanical brain as an exercise. In this book, the properties of Simon may be a good introduction to the various types of more complicated mechanical brains described in later chapters.
The rest of this chapter is devoted to such questions as:
How do transfers of information actually take place in Simon?
How does the computer in Simon work so that calculation actually occurs?
How could Simon actually be constructed?
What follows should be skipped unless you are interested in these questions and the burdensome details needed for answering them.
The first basic thinking operation for any mechanical brain is transferring information automatically. Let us see how this is done in Simon.
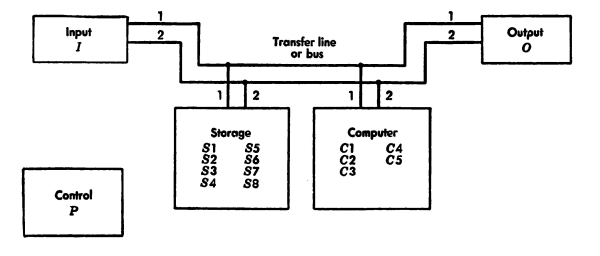
Fig. 4. Scheme of Simon.
Let us first take a look at the scheme of Simon as a mechanical brain [Pg 32] (see Fig. 4). We have 1 input, 8 storage, 5 computer, and 1 output registers, which are connected by means of transfer wires or a transfer line along which numbers or operations can travel as electrical impulses. This transfer line is often called the bus, perhaps because it is always busy carrying something. In Simon the bus will consist of 2 wires, one for carrying the right-hand digit and one for carrying the left-hand digit of any number 00, 01, 10, 11. Simon also has a number of neat little devices that will do the following:
When any number goes into a register, the coils of the relays of the register will be connected with the bus.
When any number goes out of a register, the contacts of the relays of the register will be connected with the bus.
For example, suppose that in register C5 the number 2 is stored. In machine language this is 10. That means the left-hand relay (C5-2) is energized and the right-hand relay (C5-1) is not energized. Suppose that we want to transfer this number 2 into the output register O, which has been cleared. What do we do?
Let us take a look at a circuit that will transfer the number (see Fig. 5). First we see two relays in this circuit. They belong to the C5 register. The C5-2 relay is energized since it holds 1; current is flowing through its coil, the iron core becomes a magnet, and the contact above it is pulled down. The C5-1 relay is not energized since it holds 0; its contact is not pulled down. The next thing we see is two rectifiers. The sign for these is a triangle. These are some modern electrical equipment that allow electrical current to flow in only one direction. In the diagram, the direction is shown by the pointing of the triangle along the wire. Rectifiers are needed to prevent undesired circuits. Next, we see the bus, consisting of two wires. One carries the impulses for left-hand or 2 relays, and the other carries impulses for the right-hand or 1 relays. Next, we see two relays, called the entrance relays for the O register. Current from Source 1 may flow to these relays, energize them, and close their contacts. When the first line of the program tape is read, specifying the receiving register, the code 1111 causes Source 1 to be energized. This fact is shown schematically by the arrow running from the program tape code 1111 to Source 1. Finally, [Pg 33] we see the coils of the two relays for the Output or O register. We thus see that we have a circuit from the contacts of the C5 register through the bus to the coils of the O register.

Fig. 5. Transfer circuit.
We are now ready to transfer information when the second line of the program tape is read. This line holds 1110 and designates C5 as the sending register and causes Source 2 to be energized. This fact is shown schematically by the arrow running from the second line of the program tape to Source 2. When the second line is read, current flows:
1. From Source 2.
2. Through the contacts of the C5 register if closed.
3. Through the rectifiers.
4. Through the bus.
5. Through the entrance relay contacts of the O register.
6. Through the coils of the O register relays, energizing such of them as match with the C5 closed contacts; and finally
7. Into the ground.
[Pg 34] Thus relay O-2 is energized; it receives current because contact C5-2 is closed. And relay O-1 is not energized; it receives no current since contact C5-1 is open. So we have actually transferred information from the C5 register to the O register.
The same process in principle applies to all transfers:
The pattern of electrical impulses, formed by the positioning of one register, is produced in the positioning of another register.
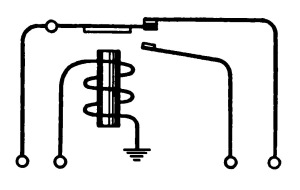
Now so far the computing registers in Simon are a mystery. We have said that C1, C2, and C3 take in numbers 00, 01, 10, 11, that C4 takes in an operation 00, 01, 10, 11, and that C5 holds the result. What process does Simon use so that he has the correct result in register C5?
Let us take the simplest computing operation first and see what sort of a circuit using relays will give us the result. The simplest computing operation is negation. In negation, a number 00, 01, 10, 11 goes into the C1 register, and the operation 01 meaning negation goes into the C4 register, and the correct result must be in the C5 register. So, first, we note the fact that the C4-2 relay must not be energized, since it contains 0, and that the C4-1 relay must be energized, since it contains 1.
Now the table for negation, with c = -a, is:
| a | c |
| 0 | 0 |
| 1 | 3 |
| 2 | 2 |
| 3 | 1 |
Negation in machine language will be:
| a | c |
| 00 | 00 |
| 01 | 11 |
| 10 | 10 |
| 11 | 01 |
[Pg 35] Now if a is in the C1 register and if c is in the C5 register, then negation will be:
| C1 | C5 |
| 00 | 00 |
| 01 | 11 |
| 10 | 10 |
| 11 | 01 |
But each of these registers C1, C5 will be made up of two relays, the left-hand or 2 relay and the right-hand or 1 relay. So, in terms of these relays, negation will be:
| C1-2 | C1-1 | C5-2 | C5-1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Now, on examining the table, we see that the C5-1 relay is energized if and only if the C1-1 relay is energized. So, in order to energize the C5-1 relay, all we have to do is transfer the information from C1-1 to C5-1. This we can do by the circuit shown in Fig. 6. (In this and later diagrams, we have taken one more step in streamlining the drawing of relay contacts: the contacts are drawn, but the coils that energize them are represented only by their names.)

Fig. 6. Negation—
right-hand digit.
Fig. 7. Negation—
left-hand digit.
Taking another look at the table, we see also that the C5-2 relay must be energized if and only if: [Pg 36]
| C1-2 HOLDS: |
AND | C1-1 HOLDS: |
| 0 | 1 | |
| 1 | 0 |
A circuit that will do this is the one shown in Fig. 7. In Fig. 8 is a circuit that will do all the desired things together: give the right information to the C5 relay coils if and only if the C4 relays hold 01.

Fig. 8. Negation circuit.
Let us check this circuit. First, if there is any operation other than 01 stored in the C4 relays, then no current will be able to get through the C4 contacts shown and into the C5 relay coils, and the result is blank. Second, if we have the operation 01 stored in the C4 relays, then the C4-2 contacts will not be energized—a condition which passes current—and the C4-1 contacts will be energized—another condition which passes current—and:
| If the number in C1 is: | then C1-1: | and C1-2: | and the C5 relays energized are: |
| 0 | does not close | does not close | neither |
| 1 | closes | does not close | C5-2, C5-1 |
| 2 | does not close | closes | C5-2 only |
| 3 | closes | closes | C5-1 only |
Thus we have shown that this circuit is correct.
We see that this circuit uses more than one set of contacts for several relays (C1-2, C4-1, C4-2); relays are regularly made with 4, 6, or 12 sets of contacts arranged side by side, all [Pg 37] controlled by the same pickup coil. These are called 4-, 6-, or 12-pole relays.
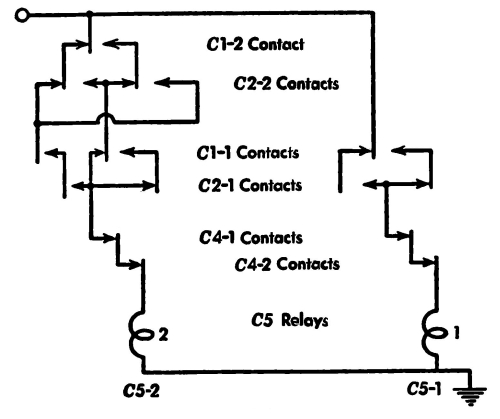
Fig. 9. Addition circuit.
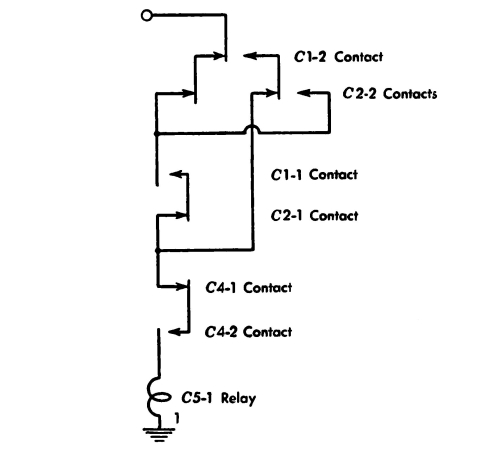
Fig. 10. Greater-than circuit.
Circuits for addition, greater than, and selection can also be determined rather easily (see Figs. 9, 10, 11). (Note: By means of the algebra of logic, referred to in Chapter 9 and Supplement 2, the conditions for many relay circuits, as well as the circuit itself, may be expressed algebraically, and the two expressions may be checked by a mathematical process.) For example, let [Pg 38] us check that the addition circuit in Fig. 9 will enable us to add 1 and 2 and obtain 3. We take a colored pencil and draw closed the contacts for C1-1 (since C1 holds 01) and for C2-2 (since C2 holds 10). Then, when we trace through the circuit, remembering that addition is stored as 00 in the C4 relays, we find that both the C5 relays are energized. Hence C5 holds 11, which is 3. Thus Simon can add 1 and 2 and make 3!
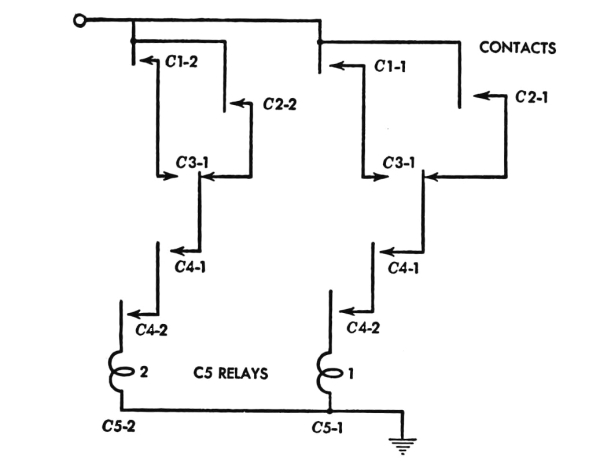
Fig. 11. Selection Circuit.
In order to put Simon together and make him work, not very much is needed. On the outside of Simon we shall need two small mechanisms for reading punched paper tape. Inside Simon, there will be about 50 relays and perhaps 100 feet of wire for connecting them. In addition to the 15 registers (I, S1 to S8, C1 to C5, and O), we shall need a register of 4 relays, which we shall call the program register. This register will store the successive instructions read off the program tape. We can call the 4 relays of this register P8, P4, P2, P1. For example, if the P8 and P2 relays are energized, the register holds 1010, and this is the program instruction that calls for the 8th plus 2nd, or 10th, register, which is C1. [Pg 39]
For connecting receiving registers to the bus, we shall need a relay with 2 poles, one for the 2-line and one for the 1-line, for each register that can receive a number from the bus. For example, for entering the output register, we actually need only one 2-pole relay instead of the two 1-pole relays drawn for simplicity in Fig. 5. There will be 13 2-pole relays for this purpose, since only 13 registers receive numbers from the bus; registers I and C5 do not receive numbers from the bus. We call these 13 relays the entrance relays or E relays, since E is the initial letter of the word entrance.
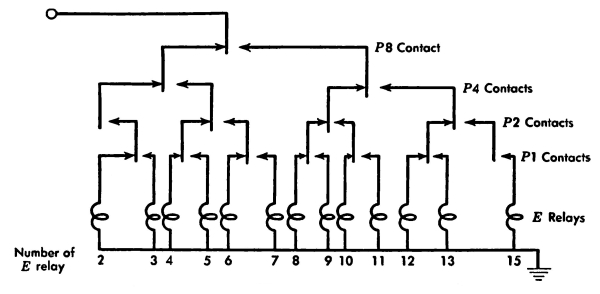
Fig. 12. Select-Receiving-Register circuit.
The circuit for selecting and energizing the E relays is shown in Fig. 12. We call this circuit the Select-Receiving-Register circuit. For example, suppose that the P8 and P2 relays are energized. Then this circuit energizes the E10 relay. The E10 relay closes the contacts between the C1 relay coils and the bus; and so it connects the C1 register to receive the next number that is sent into the bus. This kind of circuit expresses a classification and is sometimes called a pyramid circuit since it spreads out like a pyramid. A similar pyramid circuit is used to select the sending register.
We shall need a relay for moving the input tape a step at a time. We shall call this relay the MI relay, for moving input tape. We also need a relay for moving the program tape a step at a time. We shall call this relay the MP relay for moving program tape. Here then is approximately the total number of relays required: [Pg 40]
| Relays | Name | Number |
|---|---|---|
| I, S, C, O | Input, Storage, Computer, Output | 30 |
| P | Program | 4 |
| E | Entrance | 13 |
| MI | Move Input Tape | 1 |
| MP | Move Program Tape | 1 |
| Total | 49 |
A few more relays may be needed to provide more contacts or poles. For example, a single P1 relay will probably not have enough poles to meet all the need for its contacts.
Fig. 13. Latch relay.
Each cycle of the machine will be divided into 5 equal time intervals or times 1 to 5. The timing of the machine will be about as follows:
| Time | Action |
|---|---|
| 1 | Move program tape. |
| Move input tape if read out of in last cycle. | |
| 2 | Read program tape, determining the receiving register. |
| Read through the computing circuit setting up the C5 register. | |
| 3 | Move program tape. |
| Energize the E relay belonging to the receiving register. | |
| 4 | Read program tape again, determining the sending register. |
| 5 | Transfer information by reading through the |
| Select-Sending-Register circuit and the | |
| Select-Receiving-Register circuit. |
[Pg 41] In order that information may remain in storage until wanted, register relays should hold their information until just before the next information is received. This can be accomplished by keeping current in their coils or in other ways. There is a type of relay called a latch relay, which is made with two coils and a latch. This type of relay has the property of staying or latching in either position until the opposite coil is impulsed (see Fig. 13). This type of relay would be especially good for the registers of Simon.
If any reader sets to work to construct Simon, and if questions arise, the author will be glad to try to answer them.
[Pg 42]
When we think of counting, we usually think of saying softly to ourselves “one, two, three, four, ···.” This is a good way to find the total of a small group of objects. But when we have a large group of objects or a great many groups of objects to be counted, a much faster way of counting is needed. A very fast way of sorting and counting is punch-card calculating machinery. This is machinery which handles information expressed as holes in cards. Punch-card machines can:
For example, in a life insurance company, much routine handling of information about insurance policies is necessary:
Writing information on newly issued policies.
Setting up policy-history cards.
Making out notices of premiums due.
Making registers of policies in force, lapsed, died, etc., for purposes of valuation as required by law or good management.
Calculating and tabulating premium rates, dividend rates, reserve factors, etc.
Computing and tabulating expected and actual death rates; and much more.
All these operations can be done almost automatically by punch-card machines. [Pg 43]
When a census of the people of a country is taken, a great quantity of sorting and counting is needed: by village, county, city, and state; by sex; by age; by occupation; etc. In 1886, the census of the people of the United States which had been taken in 1880 was still being sorted and counted. Among the men then studying census problems was a statistician and inventor, Herman Hollerith. He saw that existing methods were so slow that the next census (1890) would not be finished before the following census (1900) would have to be begun. He knew that cards with patterns of holes had been used in weaving patterns in cloth. He realized that the presence or absence of a property, for example employed or unemployed, could be represented by the presence or absence of a hole in a piece of paper. An electrical device could detect the hole, he believed, since it would allow current to flow through, whereas the absence of the hole would stop the current. He experimented with sorting and counting, using punched holes in cards, and with electrical devices to detect the holes and count them. A definite meaning was given to each place in the card where a hole might be punched. Then electrical devices handled the particular information that the punches represented. These devices either counted or added, singly or in various combinations, as might be desired.
More than 50 years of development of punch-card calculating machinery have since then taken place. Several large companies have made quantities of punch-card machines. A great degree of development has taken place in the punch-card machines of International Business Machines Corporation (IBM), and for this reason these machines will be the ones described in this chapter. What is said here, however, may also in many ways apply to punch-card machines made by other manufacturers—Remington-Rand, Powers, Control Instrument, etc.
To use punch-card machines, we first convert the original information [Pg 44] into patterns of holes in cards. Then we feed the cards into the machines. Electrical impulses read the pattern of holes and convert them into a pattern of timed electrical currents. Actually, the reading of a hole in a column of a punch card is done by a brush of several strands of copper wire pressed against a metal roller (Fig. 1). The machine feeds the card (the bottom edge first, where the 9’s are printed) with very careful timing over the roller; and, when the punched hole is between the brush and the roller, an electrical circuit belonging to that column of the card is completed. The machine responds according to its general design and its wiring for the particular problem: it punches new cards, or it prints new marks, or it puts information into new storage places. Clerks, however, move the cards from one machine to another. They wait on the machines, keep the card feeds full, and empty the card hoppers as they fill up. A human error of putting the wrong block of cards into a machine may from time to time cause a little trouble, especially in sorting. Actually, in a year, billions of punch cards are handled precisely.

Fig. 1. Reading of punch cards.
The punch card is a masterpiece of engineering and standardization. Its exact thickness matches the knife-blade edges that feed the cards into slots in the machines, and matches the channels whereby these cards travel through the machines. The standard card is 7⅜ inches long and 3¼ inches wide, and it has a standard thickness of 0.0065 inch and other standard properties with respect to stiffness, finish, etc. [Pg 45]
Fig. 2. Scheme of standard punch card.
(Note: Positions 11 and 12 are not usually marked by printed numbers or letters.)
The standard IBM punch card of today has 80 columns and 12 positions for punching in each column (Fig. 2). A single punched hole in each of the positions known as 0 to 9 stands for each of the digits 0 to 9 respectively. The remaining 2 single punch positions available in any column are usually called the 11 position and 12 position (though sometimes called the numerical X position and Y position). These two positions do not behave arithmetically as 11 and 12. Actually, in the space between one card and the next card as they are fed through the machines, more positions occur. For example, there may be 4 more: a 10 position preceding the 9, and a 13, a 14, and a 15 position following the 12. The 16 positions in total correspond to a full turn, 360°, of the roller under the brush, and to a complete cycle in the machine; and a single position corresponds to ¹/₁₆ of 360°, or 22½°. In some machines, the total [Pg 46] number of positions may be 20. A pair of punches stands for each of the letters of the alphabet, according to the scheme shown.
| A | 12-1 | J | 11-1 | Unused | 0-1 |
| B | 12-2 | K | 11-2 | S | 0-2 |
| C | 12-3 | L | 11-3 | T | 0-3 |
| D | 12-4 | M | 11-4 | U | 0-4 |
| E | 12-5 | N | 11-5 | V | 0-5 |
| F | 12-6 | O | 11-6 | W | 0-6 |
| G | 12-7 | P | 11-7 | X | 0-7 |
| H | 12-8 | Q | 11-8 | Y | 0-8 |
| I | 12-9 | R | 11-9 | Z | 0-9 |
For example, the word MASON is shown punched in Fig. 3.

Fig. 3. Alphabetic punching.
Fig. 4. Single-panel plugboard.
To increase the versatility of the machines and provide them with instructions, many of them have plugboards (Fig. 4). These are standard interchangeable boards filled with prongs on one side and [Pg 47] holes or terminals called hubs on the other side. The side with the prongs connects to the ends of electrical circuits in the punch-card machine, which are brought together in one place for the purpose. On the other side of the board, using plugwires, we can connect the hubs to each other in different ways to produce different results. The single-panel plugboard is 10 inches long and 5¾ inches wide. It contains 660 hubs in front and 660 corresponding prongs in the back. A double-panel plugboard or a triple-panel plugboard applies to some machines. In less time than it takes to describe it, we can take one wired-up plugboard out of a machine and put in a new wired-up plugboard and thus change completely the instructions under which the machine operates. Many of the machines have a number of different switches that we must also change, when going from one kind of problem to another.
The numbers that are stored or sorted in punch-card machines may be of any size up to 80 digits, one in each column of the punch card. In doing arithmetic (adding, subtracting, multiplying, and dividing), however, the largest number of digits is usually 10. Beyond 10 digits, we can work out tricks in many cases.
The chief IBM punch-card machines are: the key punch, the verifier, the sorter, the interpreter, the reproducer, the collator, the multiplying punch, the calculating punch, and the tabulator. Of these 9 machines, the last 6 have plugboards and can do many different operations as a result.
There is a flow of punch cards through each of these machines. The machines differ from each other in the number and relation of the paths of flow, or card channels, and in the number and relation of the momentary stopping places, or card stations, at which cards are read, punched, or otherwise acted on. We can get a good idea of what a machine is from a picture of these card channels.
We use a key punch (Fig. 5) to punch original information into blank cards. In the key punch there is one card channel; it has one entrance, [Pg 48] one station, and one exit. At the card station, there are 12 punching dies, one for each position in the card column, and each card column is presented one by one for punching. The numeric keyboard (Fig. 6) for the key punch has 14 keys:
One key for each of the punches 0 to 9, 11, and 12,
A space key, which allows a column of the punch card to go by with no punch in it,
A release key, which ejects the card and feeds another card.

Fig. 5. Key punch.
Fig. 6. Keyboard of key punch.
Of course, in using a key punch, we must punch the same kind of information in the same group of columns. For example, if these cards are to contain employees’ social security numbers, we must punch that number always in the same card columns, numbered, say, 15 to 23, or 70 to 78, etc.
The verifier is really the same machine as the key punch, but it has dull punching dies moving gently instead of sharp ones moving with force. It turns on a red light and stops when there is no punched hole in the right spot to match with a pressed key.
The sorter is a machine for sorting cards, one column at a time (Fig. 7). The sorter has a card channel that forks; it has one entrance, one [Pg 49] station, and 13 exits. Each exit corresponds to: one of the 12 punch positions 0 to 9, 11, and 12; or reject, which applies when the column is nowhere punched. It has one card station where a brush reads a single column of the card. We can turn a handle and move the brush to any column.

Fig. 7. Sorter.
The interpreter takes in a card, reads its punches, prints on the card the marks indicated by the punches, and stacks the card. We call this process interpreting the card, since it translates the punched holes into printed marks. The interpreter (Fig. 8) has one card channel, with one entrance, 2 card stations, and one exit. What the machine does at the second card station depends on what the machine reads at the first card station and on what we have told the machine by switches and plugboard wiring to do.
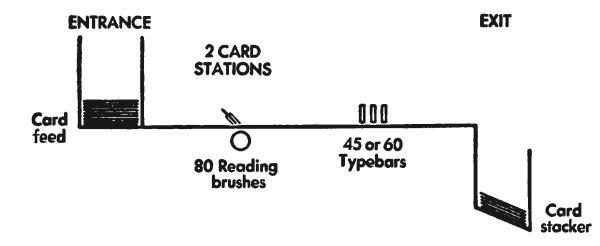
Fig. 8. Interpreter.
The reproducer or reproducing punch can: [Pg 50]
Reproduce, or copy the punches in one group of cards into another group of cards (in the same or different columns).
Compare, or make sure that the punches in two groups of cards agree (and shine a red light if they do not).
Gang punch, or copy the punches in a master card into a group of detail cards.
Summary punch, or copy totals or summaries obtained in the tabulator into blank cards in the reproducer.
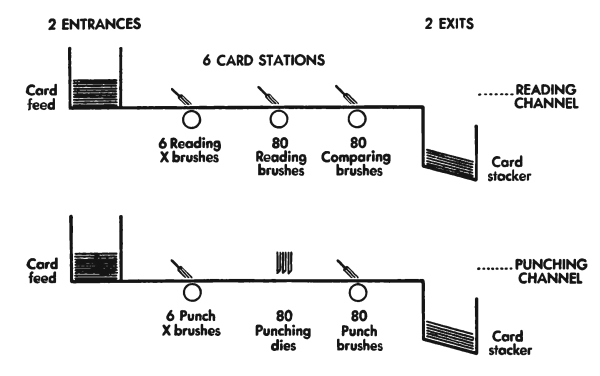
Fig. 9. Reproducer.
The reproducer (Fig. 9) has 2 independent card channels, the cards not mingling in any way, called the reading channel and the punching channel. We can run the machine with only the punching channel working; in fact, IBM equips some models only with the punching channel, particularly for “summary punch” operation. The machine is timed so that, when any card is at the middle station in either channel, then the next preceding card is at the latest station, and the next following card is at the earliest station. At 5 stations, the machine reads a card. At the middle station of the punching channel, the machine punches a card. Using a many-wire cable, we can connect the tabulator to the reproducer and so cause the tabulator to give information electrically to the reproducer. This connection makes possible the “summary punch” operation. Here is an instance with punch-card machines where, in order to transfer information from one machine to another, we are not required to move cards physically from one machine to another. [Pg 51]
The collator is a machine that arranges or collates cards. It is particularly useful in selecting, matching, and merging cards. The collator (Fig. 10) has 2 card channels which join and then fork into 4 channels ending in pockets called Hoppers 1, 2, 3, and 4. The 2 card feeds are called the Primary Feed and the Secondary Feed. Cards from the Primary Feed may fall only into the first and second hoppers. Cards from the Secondary Feed may fall only into the second, third, and fourth hoppers. The collator has 3 stations at which cards may be read.
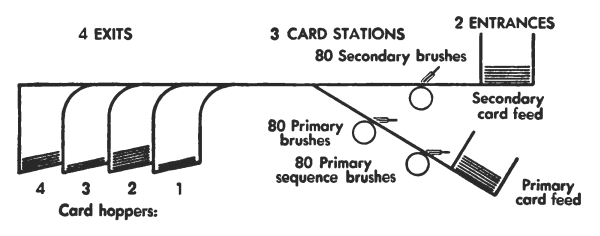
No.1—Selected primaries
No.2—Merged cards and unselected primaries
No.3—Separate secondaries not selected
No.4—Selected secondaries
Fig. 10. Collator.
IBM can supply additional wiring called the collator counting device. With this we can make the collator count cards as well as compare them. For example, we could put 12 blank cards from the Secondary Feed behind each punched-card from the Primary Feed in order to prepare for some other operation.
The calculating punch was introduced in 1946. It is a versatile machine of considerable capacity. It adds, subtracts, multiplies, and divides. It also has a control over a sequence of operations, in some cases up to half a dozen steps.
This machine (Fig. 11) has one card channel with 4 stations called, respectively, control brushes, reading brushes, punch feed, and punching dies. At station 1, there are 20 brushes; we can set these by hand to read any 20 of the 80 card columns. At station 2 there are 80 regular reading [Pg 52] brushes. At station 3 the card waits for a part of a second while the machine calculates, and, when that is done, the card is fed into station 4, where it is punched or verified. The multiplying punch is an earlier model of the calculating punch, without the capacity for division.
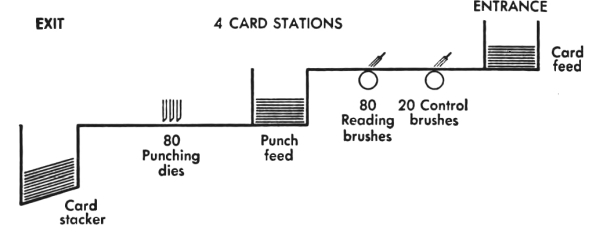
Fig. 11. Calculating punch.
The tabulator can select and list information from cards. Also, it can total information from groups of cards in counters of the tabulator and can print the totals.
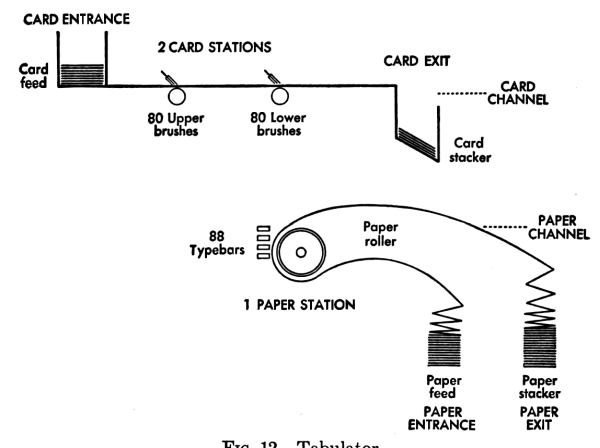
Fig. 12. Tabulator.
The tabulator (Fig. 12) has one card channel with two stations where cards may be read, called the Upper Brushes and [Pg 53] Lower Brushes. When the Lower Brush station is reading one card, the Upper Brush station is reading the next card. The tabulator also has another channel, which is for endless paper (and sometimes separate sheets or cards). This channel has one station; here printing takes place. Unlike the typewriter, the tabulator prints a whole row at a time. It can print up to 88 numerals or letters across the sheet in one stroke. The cards flowing through the card channel and the paper flowing through the paper channel do not have to move in step; in fact, we need many different time relations between them, and the number of rows printed on the paper may have almost any relation to the number of punch cards flowing through the card channel.
At the station where paper is printed, we can put on the machine a mechanism called the automatic carriage. This is like a typewriter carriage, which holds the paper for a typewriter, but we can control the movement of paper through the automatic carriage by plugboard wiring, switch settings, and holes in punch cards. Thus we can arrange for headings, spacing, and feeding of new sheets to be controlled by the information and the instructions, with a great deal of versatility.
We have now described briefly the chief available punch-card machines as of the middle of 1948. The next question is: How do we actually get something done by means of punch cards? Let us go back to the census example, even though it may not be a very typical example, and see what would be done if we wished to compile a census by punch cards.
The first thing we do is plan which columns of the punch card will contain what information about the people being counted. For example, the following might be part of the plan:
| Information | No. of Possibilities | Columns |
|---|---|---|
| State | 60 | 1-2 |
| County | 1,000 | 3-5 |
| Township | 10,000 | 6-9 |
| City or village | 10,000 | 10-13 |
| Sex | 2 | 14 |
| Age last birthday | 100 | 15-16 |
| Occupation | 100,000 | 17-21 |
| ... | ... | ... |
[Pg 54] Under the heading state, we know that there are 48 states, the District of Columbia, and several territories and possessions—all told, perhaps 60 possibilities. So, 2 punch-card columns are enough: they will allow 100 different sets of punches from 00 to 99 to be put in them. We then assign the code 00 to Maine, 01 to New Hampshire, 02 to Vermont, etc., or we might assign the code 00 to Alabama, 01 to Arizona, 02 to Arkansas, etc.—whichever would be more useful. Under the other headings, we do the same thing: count the possibilities; assign codes. In this case, it will be reasonable to use numeric codes 0 to 9 in each column in all places because we shall have millions of cards to deal with and numeric codes can be sorted faster than alphabetic codes. Alphabetic codes require 2 punched holes in each column, and sorting any column takes 2 operations.
The punch cards are printed with the chosen headings. We set up the codes in charts and give them to clerks. Using key punches and verifiers, they punch up the cards and check them. They work from the original information collected by the census-taker in the field. Since the original information will come in geographically, probably only one geographic code at a time will be needed, and it will be simple to keep track of. As to occupation, however, it may be useful to assign other clerks full-time to examining the original information and specifying the right code for the occupation. Then the clerks who do the punching will have only copying to do.
The great bulk of the work with the census will be sorting, counting, and totaling. The original punch cards will be summarized into larger and larger groups. For example, the cards for all males age 23 last birthday living in the state of Massachusetts are sorted together. This group of cards may be put into a tabulator wired to a summary punch. When the tabulator has counted the last card of this group, the summary punch punches one card, showing the total number in this group. Some time later a card like this will be ready for every state. Then the whole group of state cards may be fed into the tabulator wired to the reproducer acting as summary punch. When totaled, the number of males age 23 last birthday in the United States will be punched into a single card. After more compiling, a card like this will be ready for all [Pg 55] males in the United States at each age. Then this group of cards may be fed into the tabulator wired to the summary punch. Each card may be listed by the tabulator on the paper flowing through it, showing the age and the number of males living at that age. At the end of the listing, the tabulator will print the total number of all males in the list, and the summary punch will punch a card containing this total.
Punch-card machines can perform the arithmetical operations of counting, adding, subtracting, multiplying, dividing, and rounding off.
Counting can be done by the sorter, the tabulator, and the collator. The tabulator can print the total count. The tabulator and summary punch wired together can put the total count automatically into another punch card. The sorter shows the count in dials.
Adding and subtracting can be done by the tabulator, the calculating punch, and the multiplying punch. In the calculating and multiplying punches, the sum or difference is usually punched into the same card from which the numbers were first obtained. The tabulator, however, obtains the result first in a counter; from the counter, it can be printed on paper or punched into a blank card with the aid of the summary punch.
Numbers are handled as groups of decimal digits, and the machines mirror the properties of digits in the decimal system. Negative numbers are usually handled as complements (see Supplement 2). For example, if we have in the tabulator a counter with a capacity of six digits, the number-000013 is stored in the counter as the complement 999987. We cannot store in the counter the number +999987, since we cannot distinguish it from-000013. In other words, if a counter is to be used for both positive and negative numbers, its capacity is actually one digit less, since in the last decimal place on the left 0 will mean positive and 9 will mean negative. [Pg 56]
Multiplying is done in the calculating and multiplying punches. In both cases, the multiplication table is built into the circuits of the machine, and the system of left-hand components and right-hand components is used (see Supplement 2).
Dividing is done in the calculating punch and is carried out in that machine much as in ordinary arithmetic. By means of an estimating circuit the calculating punch guesses what multiple of the divisor will go into the dividend. Then it determines that multiple and tries it.
Rounding off may be done in 3 punch-card machines, the calculating and multiplying punches, and the tabulator. For example, suppose we have the numbers 49.1476, 68.5327, and we wish to round them off to 2 decimal places. The results will be 49.15 and 68.53. For the first number, we raise the .0076, turning .1476 into .15, since .0076 is more than .005. For the second number, we drop the .0027 since it is less than .005.
Each of these punch-card machines provides what is called a 5 impulse in each machine cycle. When the number is to be rounded off, the 5 impulse is plugged into the first decimal place that is to be dropped, and it is there added. If the figure in the decimal place to be dropped is 0 to 4, the added 5 makes no difference in the last decimal place that is to be kept. But, if the figure in the decimal place to be dropped is 5 to 9, then the added 5 makes a carry into the last decimal place that is to be kept, increasing it by 1, and this is just what is wanted for rounding off.
Punch-card machines do many operations of reasoning or logic that do not involve addition, subtraction, multiplication, or division. Just as we can write equations for arithmetical operations, so we can write equations for these logical operations using mathematical logic (see Chapter 9 and Supplement 2). If any reader, however, is not interested in these logical equations, he should skip each paragraph that begins with “in the language of logic,” or a similar phrase. [Pg 57]
Reading and writing are operations perhaps not strictly of reasoning but of translating from one language to another. Basically these operations take in a mark in one language and give out a mark with the same meaning in another language. For example, the interpreter takes in punched holes and gives out printed marks, but the holes and the marks have the same meaning.
The major part of sorting is done by a punch-card sorting machine and can be considered an operation of translating. In sorting a card, the machine takes in a mark in the form of a punched hole on a punch card and specifies a place bearing the same mark where the card is put. The remaining part of sorting is done by human beings. This part consists of picking up blocks of cards from the pockets of the sorter and putting the blocks together in the right sequence.

Fig. 13. Comparer.
The first operation of reasoning done by punch-card machines is comparing. For an example of comparing in the operation of the tabulator, let us take instructing the machine when to pick up a total and print it. As an illustration, suppose that we are making a table by state, county, and township of the number of persons counted in a census. Suppose that for each township we have one punch card telling the total number of persons. If all the cards are in sequence, then, whenever the county changes, we want a minor total, and, whenever the state changes, we want a major total. What does the machine do?
The tabulator has a mechanism that we shall call a comparer (Fig. 13). A comparer has 2 inputs that may be called Previous and Current and one output that may be called Unequal. The comparer has the property of giving out an impulse if and only if there is a difference between the 2 inputs. [Pg 58]
In the language of the algebra of logic (see Supplement 2 and Chapter 9), let the pieces of information coming into the comparer be a and b, and let the information coming out of the comparer be p. Then the equation of the comparer is:
p = T(a ≠ b)
where “T (···)” is “the truth value of ···” and “···” is a statement, and where the truth value is 1 if true and 0 if false.
In wiring the tabulator so that it can tell when to total, we use the comparer. We feed into it the county from the current card and the county from the previous card. Out of the comparer we get an impulse if and only if these two pieces of information are different. This is just what happens when the county changes. The impulse from the comparer is then used in further wiring of the tabulator: it makes the counter that is busy totaling the number of persons in the county print its total and then clear. In the same way, another comparer, which watches state instead of county, takes care of major totals when the state changes.
The next operation of reasoning which punch-card machines can do is selecting. The tabulator, collator, interpreter, reproducer, and calculating punch all may contain mechanisms that can select information. These mechanisms are called selectors.
For example, suppose that we are using the tabulator to make a table showing for each city the number of males and the number of females. In the table we shall have three columns: first, city; second, males; third, females. Suppose that each punch card in columns 30 to 36 shows the total of males or females in a city. Suppose that, if and only if the card is for females, it has an X punch (or 11 punch) in column 79. What do we want to have happen? We want the number in columns 30 to 36 to go into the second column of the table if there is no X in column 79, and we want it to go into the third column of the table if there is an X in column 79. This is just another way of saying that we want the number to go into the males column if it is a number of males, and into the females column if it is a number of females. We make this happen by using a selector. [Pg 59]
A selector (Fig. 14) is a mechanism with 2 inputs and 2 outputs. The 2 inputs are called X Pickup and Common. The 2 outputs are called X and No X. The X Pickup, as its name implies, watches for X’s. The Common takes in information. What comes out of X is what goes into Common if and only if an X punch is picked up; otherwise nothing comes out. What comes out of No X is what goes into Common if and only if an X punch is not picked up; otherwise nothing comes out. From the point of view of ordering punch-card equipment, we should note that there are two types of selectors: X selectors or X distributors, which have a selecting capacity of one column—that is, one decimal digit—and class selectors, which ordinarily have a selecting capacity of 10 columns or 10 decimal digits. But we shall disregard this difference here, as we have disregarded most other questions of capacity in multiplication, division, etc.

Fig. 14. Selector.
In the language of logic (see Chapter 9 and Supplement 2), if p, a, b, c are the information in X Pickup, Common, X, and No X, respectively, then the equations for a selector are:
b = a·p
c = a·(1 - p)
Returning now to the table we wish to make, we connect columns 30 to 36 of the punch card to Common. We connect column 79 of the punch card to the X Pickup. We connect the output No X to the males column of the table. We connect the output X to the females column of the table. In this way we make the number in the punch card appear in either one of two places in the table according to whether the number counts males or females.
We might mention several more properties of selectors. A selector can be used in the reverse way, with X Pickup, X, and No X as inputs and [Pg 60] Common as output (Fig. 15). What will come out of Common is (1) what goes into input No X if there is no X punch in the column to which input X Pickup is wired, and (2) what goes into input X if there is an X punch in the column to which input X Pickup is wired.
In this case the logical equation for the selector is:
a = bp + c(1 - p)
Also, selectors can be used one after another, so that selecting based on 2 or 3 X punches can be made.

Fig. 15. Selector.
In the language of logic, if p, q, r are the truth values of “there is an X punch in column i, j, k,” respectively, then by means of selectors we can get such a function as:
c = apq + b(1 - q)(1 - r)
Also, a selector may often be energized not only by an X punch but also by a punch 0, 1, 2, ···, 9 and 12. In this case, the selector is equipped with an additional input that can respond to any digit. This input is called the Digit Pickup.
Something like an ordinary selector is another mechanism called a digit selector (Fig. 16). This has one input, Common, and 12 outputs, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12. This mechanism is often included in the tabulator and may be included in other punch-card machines. For example, suppose that we want to do something if and only if column 62 of a punch card contains a 3 or a 4 or a 9. Then we connect a brush that reads column 62 of the punch card to the Common input of the digit selector. And we connect out from the digit selector jointly from outputs 3, 4, and 9.
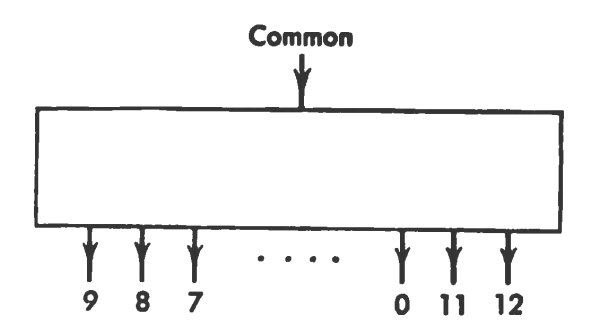
Fig. 16. Digit selector.
[Pg 61] In the language of logic, if a is the digit going into Common, and if p is the impulse coming out of the digit selector, then the equation of the mechanism in this case is:
p = T(a = 3, 4, 9)
A fourth operation of reasoning done by punch-card machines is finding that one number is greater than, or equal to, or less than another. This operation is done in the collator and may be called sequencing. For example, suppose that we have a file of punch cards for cities, showing in columns 41 to 48 the number of people. Suppose that we wish to pick out the cards for cities over 125,000 in population. Now the collator has a mechanism that has 2 inputs and 3 outputs (Fig. 17). We may call this mechanism a sequencer, since it can tell the sequence of two numbers. What goes into the Primary input is a number: let us call it a. What goes into Secondary is another number: let us call it b. An impulse comes out of Low Primary if a is less than b. An impulse comes out of Equal if a equals b. An impulse comes out of Low Secondary if a is greater than b.
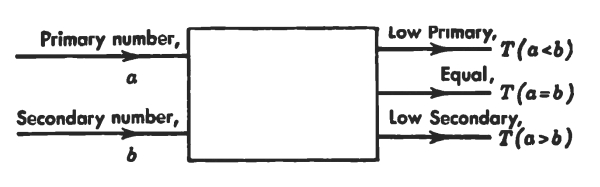
Fig. 17. Sequencer.
In the language of logic, if p, q, r are the three indications in Low Primary, Equal, and Low Secondary, then:
p = T(a < b)
q = T(a = b)
r = T(a > b)
Returning to our example, we punch up a card with 125,000 in columns 43 to 48, and we put this card into the Secondary Feed. We take the punch cards for cities and put them into the Primary Feed. In the plugboard, [Pg 62] we connect the hubs of the Secondary Brushes (that read the card in the Secondary Feed), columns 43 to 48, to the Secondary input of the Sequencer. We connect the hubs of the Primary Brushes (that read the card in the Primary Feed), columns 41 to 48, to the Primary input of the Sequencer. Then we connect the Low Primary output of the Sequencer to a device that causes the city card being examined to fall into pocket 1. We connect Equal output and Low Secondary output to a device that causes the city card being examined to fall into pocket 2. Then, when the card for any city comes along, the machine compares the number of people in the city with 125,000. If the number is greater than 125,000, the card will fall into pocket 1; otherwise the card will fall into pocket 2. At the end of the run, we shall find in pocket 1 all the cards we want.
We may expect to see over the next few years major developments in punch-card machinery. It would seem likely that types of punch-card machines like the following might be constructed:
A punch-card machine that performs any arithmetical or logical operation at high speed and may perform a dozen such operations in sequence during the time that a punch card passes through the machine.
A punch-card machine that uses loops of punched paper tape, which express either a sequence of values in a table that the machine can consult or a sequence of instructions that govern the operations of the machine.
Punch-card machinery that uses a larger card than the 80-column card.
A punch-card machine that may have a fairly large amount of internal memory, perhaps 30 or 40 registers where numbers or words may be stored and referred to.
The speed of various operations with present IBM punch-card machines is about as shown in the table. [Pg 63]
| Machine | Operation | Time in Seconds |
|---|---|---|
| Key punch | Punch 80 columns | About 20 to 40 |
| Verifier | Check 80 columns | About 20 to 40 |
| Sorter | Sort 1 card on 1 column | 0.15 |
| Interpreter | Print 1 line | 0.8 |
| Reproducer | Reproduce a card, all 80 columns | 0.6 |
| Collator | Merge 2 cards | 0.25 |
| Multiplying punch | Multiply by 8 digits | 5.6 |
| Calculating punch | Add | 0.3 |
| Calculating punch | Multiply by 8 digits | 3.6 |
| Calculating punch | Divide, obtaining 8 quotient digits | 9.0 |
| Tabulator | Print 1 line, numbers only | 0.4 |
| Tabulator | Print 1 line, letters included | 0.75 |
| Tabulator | Add numbers from 1 card | 0.4 |
Punch-card machines may be either rented or purchased from some manufacturers but only rented from others. If we take the cost of a clerk as $120 to $150 a month, the monthly rent of most punch-card machines ranges from ⅒ of the cost of a clerk for the simplest type of machine, such as a key punch, to 3 times the cost of a clerk for a complicated and versatile type of machine, such as a tabulator with many attachments. The rental basis is naturally convenient for many kinds of jobs.
The reliability of work with punch cards and punch-card machines is often much better than 99 per cent: in 10,000 operations, failures should be less than 2 or 3. This is, of course, much better than with clerical operations.
There are a number of causes for machine or card failures. Sometimes cards may be warped and may not feed into the machines properly. Or, the air in the room may be very dry, and static electricity may make the cards stick together. Or, the air may be too humid; the cards may swell slightly and may jam in the machine. A punch may get slightly out of true alignment, and punches in the cards may be slightly off. A relay may get dust on its contact points and, from time to time, fail to perform in the right way. Considerable engineering effort has been [Pg 64] put into remedying these and other troubles, with much success.
To make sure that we have correct results from human beings working with punch-card machines, we may verify each process. Information that is punched on the key punch may be verified on the verifier. Multiplications done with multiplicand a and multiplier b may be repeated and compared with multiplications done with multiplicand b and multiplier a. Cards that are sorted on the sorter may be put through the collator to make sure that their sequence is correct. It is often good to plan every operation so that we have a proof that the result is right.
It is standard practice to have the machines inspected regularly in order to keep them operating properly. On the average, for every 50 to 75 machines, there will be one full-time service man maintaining them and taking care of calls for repairs. Of course, as with any machinery, some service calls will be a result of the human element; for example, a problem may have been set up wrongly on a machine.
Punch-card calculations are much faster and more accurate than hand calculations. With punch cards, work is organized so that all cases are handled at the same time in the same way. This process is very different from handling each case separately from start to finish. As soon as the number of cases to be handled is more than a hundred and each item of information is to be used five or more times, punch cards are likely to be advantageous, provided other factors are favorable. Vast quantities of information have been handled very successfully by punch-card machines. Over 30 scientific and engineering laboratories in the United States are doing computation by punch cards. Over a billion punch cards, in fact, are used annually in this country.
[Pg 65]
In the previous chapter we talked about machines that move information expressed as holes in cards. In this chapter we shall talk about machines that move information expressed as measurements.
A simple example of a device that uses a measurement to handle information is a doorpost. Here the height of a child may be marked from year to year as he grows (Fig. 1). Or, suppose that we have a globe of the world and wish to find the shortest path between Chicago and Moscow. We may lay a piece of string on the globe, pull it tight between those points, and then measure the string on a scale to see about what distance it shows (Fig. 2).
Machines that handle information as measurements of physical quantities are called analogue machines, because the measurement is analogous to, or like, the information. A common example of analogue machine is the slide rule. With this we calculate by noting the positions of ruled lines on strips that slide by each other. These strips are made of fine wood, or of plastic, or of steel, in such fashion that the ruled lines will hold true positions and not warp. If we space the rulings so that 1, 2, 3, 4, 5, 6 ··· are equally spaced, then the slide rule is useful for addition (Fig. 3). But if we space the rulings so that powers (for example, powers of two—1, 2, 4, 8, 16, 32 ···) (Fig. 4) are equally spaced, we can do multiplication. The spacings are then according to the logarithms of numbers (see Supplement 2). Multiplication is more troublesome than addition, and so more slide rules are made for multiplication than for addition. [Pg 66]
Fig. 1. Measurement by doorpost.

Fig. 2. Measurement by string.
[Pg 67]
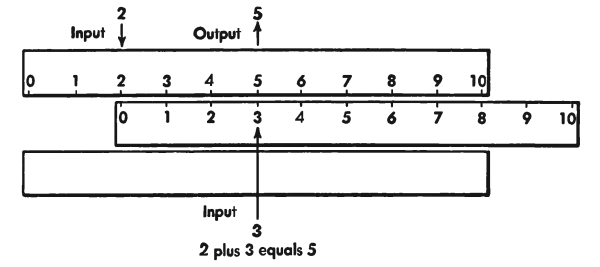
Fig. 3. Slide Rule for adding.
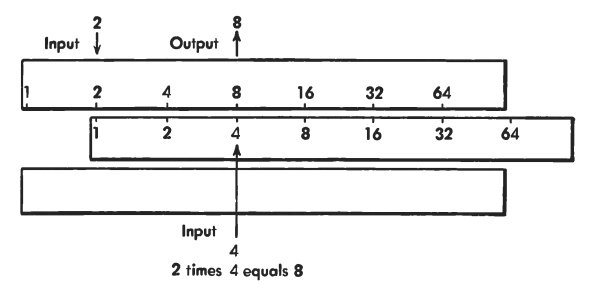
Fig. 4. Slide Rule for multiplying.
During World War II, the aiming and firing of guns against hostile planes was done by machine. After sighting a plane, these machines automatically calculated how to direct fire against it. They were much better and faster than any man. These fire-control instruments were analogue machines with steel and electrical parts built to fine tolerances. With care we can get accuracy of 1 part in 10,000 with analogue machines, but greater accuracy is very hard to get.
Suppose that we wish to make an analogue machine. We need to represent information by a measurement of something. What should we select? What [Pg 68] physical thing to be measured should we choose to put into the machine? Different amounts of this physical quantity will match with different amounts of the measurement being expressed. In the case of the doorpost, the string, and the slide rule, the physical quantity is distance. In many fire-control instruments, the physical quantity is the amount of turning of a shaft (Fig. 5). Many other physical quantities have from time to time been used in analogue machines, such as electrical measurements. The speedometer of an automobile tells distance traveled and speed. It is an analogue machine. It uses the amount of turning of a wheel, and some electrical properties. It handles information by means of measurements. The basic physical quantity that it measures is the amount of turning of a shaft.
Fig. 5. Measurement by amount of turning of a shaft.
The biggest and cleverest mechanical brain of the analogue type which has yet been built is the differential analyzer finished in 1942 at Massachusetts Institute of Technology in Cambridge, Mass. The fundamental physical quantity used in this machine is the amount of turning of a shaft. The name analyzer means an apparatus or machine for analyzing or solving problems. It happens that the word “analyzer” has been used rather more often in connection with analogue machines, and so in many cases the word “analyzer” carries the meaning “analogue” as well. The word “differential” in the phrase “differential analyzer” refers to the main purpose of the machine: it is specially adapted for solving problems involving differential equations. Now what is a differential equation?
In order to explain what a differential equation is, we need to use certain ideas. These ideas are: equation; formula; function; rate of change; interval; [Pg 69] derivative; and integral. In the next few paragraphs, we shall introduce these ideas briefly, with some explanation and examples. It is entirely possible for anyone to understand these ideas rather easily, by collecting true statements about them; no one should feel that because these ideas may be new they cannot be understood readily.
In physics, chemistry, mechanics, and other sciences there are many problems in which the behavior of distance, of time, of speed, heat, volume, electrical current, weight, acceleration, pressure, and many other physical quantities are related to each other. Examples of such problems are:

Fig. 6. Paths of a shot from a gun, trajectories.
What are the various angles to which a gun should be raised in order that it may shoot various distances? (See Fig. 6.) (The paths of a shot from a gun are called trajectories.)
If a plane flies in a direction always at the same angle from the north, how much farther will it travel than if it flew along the shortest path? (See Fig. 7.) (A path always at the same angle from the north is called a loxodrome, and a shortest path on a globe is called a great circle.)
How should an engine be designed so that it will have the least vibration when it moves fast?
[Pg 70] In physical problems like these, the answer is not a single number but a formula. What we want to do in any one of these problems is find a formula so that any one of the quantities may be calculated, given the behavior of the others. For example, here is a familiar problem in which the answer is a formula and not a number:
Fig. 7. Paths of a flight.
Fig. 8. Room formulas.
How are the floor area of a room, its length, and its width related to each other? (See Fig. 8.)
The answer is told in any one of three equations:
(floor area) equals (length) times (width)
(length) equals (floor area) divided by (width)
(width) equals (floor area) divided by (length)
The first equation shows that the floor area depends on the length of the room and also on the width of the room. So we say floor area is a function of length and width. This particular function happens to be product, the result of multiplication. In other words, floor area is equal to the product of length and width.
Now there is another kind of function called a differential function or derivative. A differential function or derivative is an instantaneous rate of change. An instantaneous rate of change is the result of two steps: (1) finding a rate of change over an interval and then (2) letting the interval become smaller and smaller indefinitely. For example, suppose that we have the problem:
How are speed, distance, and time related to each other?
[Pg 71] One of the answers is:
(speed) equals the instantaneous rate of change of (distance) with respect to (time)
Or we can say, and it is just the same thing in other words:
(speed) equals the derivative of (distance) with respect to (time)
Now we can tell what a differential equation is. It is simply an equation in which a derivative occurs, such as the last example. Perhaps the commonest kind of equation in physical problems is the differential equation.
Now we were able to change the equation about floor area into other forms, if we wanted to find length or width instead of floor area. When we did this, we ran into the inverse or opposite of multiplication: division.
In the same way, we can change the equation about speed into other forms, if we want to find distance or time instead of speed. If we do this, we run into a new idea, the inverse or opposite of the derivative, called integral. The two new equations are:
(distance) equals the integral of (speed) with respect to (time)
(time) equals the integral of [one divided by (speed)] with respect to (distance)
These equations may also be called differential equations.
An integral is the result of a process called integrating. To integrate speed and get distance is the result of three steps: (1) breaking up an interval of time into a large number of small bits, (2) adding up all the small distances that we get by taking each bit of time and multiplying by the speed which applied in that bit of time, and (3) letting the bits of time get smaller and smaller, and letting the number of them get larger and larger, indefinitely. [Pg 72]
In other words,
(total distance) equals the sum of all the small (distances), each equal to: a bit of (time) multiplied by the (speed) applying to that bit
This is another way of saying as before,
(distance) equals the integral of (speed) with respect to (time)
To solve a differential equation, we almost always need to integrate one or more quantities.
For at least two centuries, solving differential equations to answer physical problems has been a main job for mathematicians. Mathematics is supposed to be logical, and perhaps you would think this would be easy. But mathematicians have been unable to solve a great many differential equations; only here and there, as if by accident, could they solve one. So they often wished for better methods in order to make the job easier.
A British mathematician and physicist, William Thomson (Lord Kelvin), in 1879 suggested solving differential equations by a machine. He went further: he described mechanisms for integrating and other mathematical processes, and how these mechanisms could be connected together in a machine. No such machine was then built; engineering in those years was not equal to it. In 1923, a machine of this type for solving the differential equations of trajectories was proposed by L. Wainwright.
In 1925, at Massachusetts Institute of Technology, the problem of a machine to solve differential equations was again being studied by Dr. Vannevar Bush and his associates. Dr. Bush experimented with mechanisms that would integrate, add, multiply, etc., and methods of connecting them together in a machine. A major part of the success of the machine depended on a device whereby a very small turning force would do a rather large amount of work. He developed a way in which the small [Pg 73] turning force, about as small as a puff of breath, could be used to tighten a string around a drum already turning with a considerable force, and thus clutch the drum, bring in that force, and do the work that needed to be done. You may have watched a ship being loaded, seen a man coil a rope around a winch, and watched him swing a heavy load into the air by a slight pull on the rope (Fig. 9). If so, you have seen this same principle at work. The turning force (or torque) that pulls on the rope is greatly increased (or amplified) by such a mechanism, and so we call it a torque amplifier.
Fig. 9. Increasing turning force;
winch, or torque amplifier.
By 1930, Dr. Bush and his group had finished the first differential analyzer. It was entirely mechanical, having no electrical parts except the motors. It was so successful that a number of engineering schools and manufacturing businesses have since then built other machines of the Bush type. Each time, some improvements were made in accuracy and capacity for solving problems. But, if you changed from one problem to another on this type of machine, you had to do a lot of work with screwdrivers and wrenches. You had to undo old mechanical connections between shafts and set up new ones. Accordingly, in 1935, the men at MIT started designing a second differential analyzer. In this one you could make all the connections electrically.
MIT finished its second differential analyzer in 1942, but the fact was not published during World War II, for the machine was put to work on important military problems. In fact, a rumor spread and was never denied that the machine was a white elephant and would not work. The machine was officially announced in October 1945. It was the most advanced and efficient differential analyzer ever built. We shall talk chiefly about it for the rest of this chapter. A good technical [Pg 74] description of this machine is in a paper, “A New Type of Differential Analyzer,” by Vannevar Bush and Samuel H. Caldwell, published in the Journal of the Franklin Institute for October 1945.
A differential analyzer is basically made up of shafts that turn. When we set up the machine to solve a differential equation, we assign one shaft in the machine to each quantity referred to in the equation. It is the job of that shaft to keep track of that quantity. The total amount of turning of that shaft at any time while the problem is running measures the size of that quantity at that time. If the quantity decreases, the shaft turns in the opposite direction. For example, if we have speed, time, and distance in a differential equation, we label one shaft “speed,” another shaft “time,” and another shaft “distance.” If we wish, we may assign 10 turns of the “time” shaft to mean “one second,” 2 turns of the “distance” shaft to mean “one foot,” and 4 turns of the “speed” shaft to mean “one foot per second.” These are called scale factors. We could, however, use any other convenient units that we wished.
By just looking at a shaft or a wheel, we can tell what part of a full turn it has made—a half, or a quarter, or some other part—but we cannot tell by looking how many full turns it has made. In the machine, therefore, there are mechanisms that record not only full turns but also tenths of turns. These are called counters. We can connect a counter to any shaft. When we want to know some quantity that a shaft and counter are keeping track of, we read the counting mechanism.
The second differential analyzer, which MIT finished in 1942, went a step further than any previous one. In this machine, a varying number can be expressed either (1) mechanically as the amount of turning of a shaft, or (2) electrically as the amount of two voltages in a pair of wires. The MIT men did this by means of a mechanism called an angle-indicator.
Angle indicators have essentially three parts: a transmitter, a receiver, and switches. The transmitter (Fig. 10) can sense the exact amount that a shaft has turned and give out a voltage in each of [Pg 75] two wires which tells exactly how much the shaft has turned (Fig. 11). The receiving device (Fig. 12), which has a motor, can take in the voltages in the two wires and drive a second shaft, making it turn in step with the first shaft. By means of the switchboard (Fig. 13), the two wires from the transmitter of any angle-indicator can lead anywhere in the machine and be connected to the receiver of any other angle indicator.
Fig. 10. Scheme of angle-indicator transmitter.
Fig. 11. Indication of angle.

Fig. 12. Scheme of angle-indicator receiver.
In a differential analyzer, we can connect the shafts together in many different ways. For example, suppose that we want one shaft b to turn twice as much as another shaft a. For this to happen we must have a mechanism that will connect shaft a to shaft b and make shaft b turn twice as much as shaft a. We can draw the scheme of this mechanism in Fig. 14: a box, standing for any kind of simple or complicated mechanism; a line going into it, standing for input of the quantity a; a line going out of it, standing for output of the quantity b; and a statement saying that b equals 2a. [Pg 76]
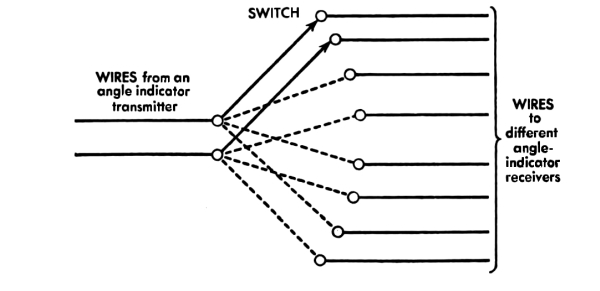
Fig. 13. Switchboard.
One mechanism that will make shaft b turn twice as much as shaft a is a pair of gears such that: (1) they mesh together and (2) the gear on shaft a has twice as many teeth as the gear on shaft b (Fig. 15). On the mechanical differential analyzer that MIT finished in 1930, a pair of gears was the mechanism actually used for doubling. To make one shaft turn twice as much as another by this device, we would: go over to the machine with a screwdriver; pick out from a box two gears, one with twice as many teeth as the other; slide them onto the shafts that are to be connected; make the gears mesh together; and screw them tight on their shafts.
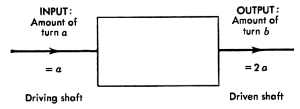
Fig. 14. Scheme of a doubling
mechanism.
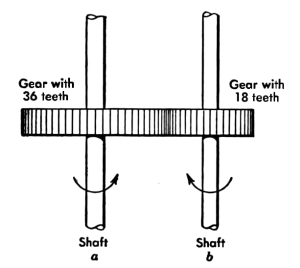
Fig. 15. Example of a doubling
mechanism.
On the MIT differential analyzer No. 2, however, we are better off. A much more convenient device for doubling is used. We make use of: a [Pg 77] gearbox in whichthere are two shafts that may be geared so that one turns twice as much as the other, and two angle-indicator transmitters and receivers. Looking at the drawing (Fig. 16), we can see that: shaft a drives shaft c to turn in step, shaft c drives shaft d to turn twice as much, and shaft d drives shaft b to turn in step. Here we can accomplish doubling by closing the pairs of switches that connect to the gearbox shafts.
Angle indicators: T, transmitters, and R, receivers
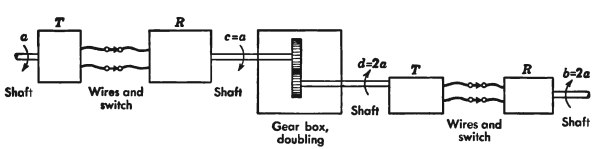
Fig. 16. Another example of a doubling mechanism.
Above, we have talked about a mechanism with gears that would multiply the amount of turning by the constant ratio 2. But, of course, in a calculation, any ratio, say 7.65, 3.142, ···, might be needed, not only 2. In order to handle various constant ratios, gearboxes of two kinds are in differential analyzer No. 2. The first kind is a one-digit gearbox. It can be set to give any of 10 ratios, 0.1, 0.2, 0.3, ···, 1.0. The second kind is a four-digit gearbox. It can be set to give any one of more than 11 thousand ratios, 0.0000, 0.0001, 0.0002, ···, 1.1109, 1.1110. We can thus multiply by constant ratios.
We come now to a new mechanism, whose purpose is to add or subtract the amount of turning of two shafts. It is called an adder. The scheme of it is shown in Fig. 17: an input shaft [Pg 78] with amount of turning a, another input shaft with amount of turning b, and an output shaft with amount of turning a + b. The adder essentially is another kind of gearbox, called a differential gear assembly. This name is confusing: the word “differential” here has nothing to do with the word “differential” in “differential analyzer.” This mechanism is very closely related to the “differential” in the rear axle of a motor car, which distributes a driving thrust from the motor to the two rear wheels of the car.
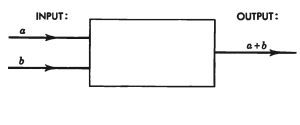
Fig. 17. Scheme of an adder mechanism.

Fig. 18. Example of an adding mechanism
(differential gear assembly).
A type of differential gear assembly that will add is shown in Fig. 18. This is a set of 5 gears A to E. The 2 gears A and B are input gears. The amount of their turning is a and b, respectively. They both mesh with a third gear, C, free to turn, but the axis of C is fastened to the inside rim of a fourth, larger gear, D. Thus D is driven, and the amount of its turning is (a + b)/2. This gear meshes with a gear E with half the number of teeth, and so the amount of turning of E is a + b.
We can subtract the turning of one shaft from the turning of another simply by turning one of the input shafts in the opposite direction.
Another mechanism in a differential analyzer, and the one that makes it worth while to build the machine, is called an integrator. This mechanism carries out the process of integrating, of adding up a very large number of small changing quantities. Figure 19 shows what an integrator is. It has three chief parts: a disc, a little wheel, and a screw. The round disc turns horizontally on its vertical shaft. The wheel rests on the disc and turns vertically on its horizontal shaft. The screw goes through the [Pg 79] support of the disc; when the screw turns, it changes the distance between the edge of the wheel and the center of the disc.

Fig. 19. Mechanism of integrator.
Now let us watch this mechanism move. If the disc turns a little bit, the wheel pressing on it must turn a little bit. If the screw turns a small amount, the distance between the edge of the wheel and the center of the disc changes. The amount that the wheel turns is doubled if its distance from the center of the disc is doubled, and halved if that distance is halved. So we see that:
(the total amount that the wheel turns) equals the sum of all the small (amounts of turning), each equal to: a bit of (disc turning) multiplied by the (distance from the center of the disc to the edge of the wheel) applying to that bit
If we look back at our discussion of integrating (p. 72), we see that the capital words here are just the same as those used there. Thus we have a mechanism that expresses integration:
(the total amount that the wheel turns) equals the integral of (the distance from the center of the disc to the wheel) with respect to (the amount that the disc turns)
The scheme of this mechanism is shown in Fig. 20.
For example, suppose that the screw measures the speed at which a car [Pg 80] travels and that the disc measures time. The wheel, consequently, will measure distance traveled by the car. The mechanism integrates speed with respect to time and gives distance.
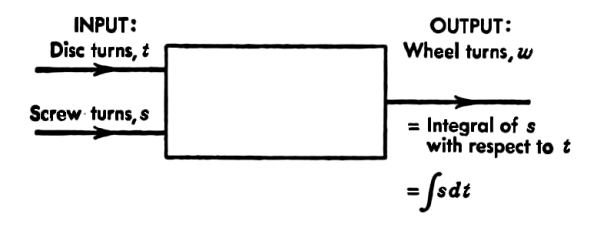
Fig. 20. Scheme of integrator.
This mechanism is the device that Lord Kelvin talked about in 1879 and that Dr. Bush made practical in 1925. The mechanical difficulty is to make the friction between the disc and the wheel turn the wheel with enough force to do other work. In the second differential analyzer, the angle indicator set on the shaft of the wheel solves the problem very neatly.
Fig. 21. Graph of air resistance coefficient.
The behavior of some physical quantities can be described only by a series of numbers or a graphic curve. For example, the resistance or drag of the air against a passing object is related to the speed of the object in a rather complicated way. Part of the relation is called the drag coefficient or resistance coefficient; a rough graph of this is shown in Fig. 21. This graph shows several interesting facts: (1) when the object is still, there is no air resistance; (2) as it travels faster and faster, air resistance rapidly increases; (3) when the object travels with the [Pg 81] speed of sound, resistance is very great and increases enormously; (4) but, when the object starts traveling with a speed about 20 per cent faster than sound, the drag coefficient begins to decrease. This drawing or graph shows in part how air resistance depends on speed of object; in other words, it shows the drag coefficient as a function of speed (see Supplement 2).
Fig. 22. Pointer following graph.
Now we need a way of putting any function we wish into a differential analyzer. To do this, we use a mechanism called a function table. We draw a careful graph of the function according to the scale we wish to use, and we set the graph on the outside of a large drum (Fig. 22). For example, we can put the resistance coefficient graph on the drum; the speed (or independent variable) goes around the drum, and the resistance coefficient (or dependent variable) goes along the drum. The machine slowly turns the drum, as may be called for by the problem. A girl sits at the function table and watches, turning a handwheel that keeps the sighting circle of a pointer right over the graph. The turning of the handwheel puts the graphed function into the machine. Instead of employing a person, we can make one side of the graph black, leaving the other side white, and put in a phototube (an electronic tube sensitive to amount of light) that will steer from pure black or pure white to half and half (see Fig. 23).
We do not need many function tables to put in information, because we can often use integrators in neat combinations to avoid them. We shall say more about this possibility later.
We can also use a function table to put out information and to draw a graph. To do so, we disconnect the handwheel; we connect the shaft of [Pg 82] the handwheel to the shaft that records the function we are interested in; we take out the pointer and put in a pen; and we put a blank sheet of graph paper around the drum.
Fig. 23. Phototube following graph.
We have now described the main parts of the second MIT differential analyzer. They are the parts that handle numbers. We can now tell the capacity of the differential analyzer by telling the number of main parts that it holds:
| Shafts | About 130 |
| One-digit gearboxes | 12 |
| Four-digit gearboxes | 16 |
| Adders | About 16 |
| Integrators | 18 |
| Function tables | 3 |
On a simpler level, we can say that the machine holds these physical parts:
| Miles of wire | About 200 |
| Relays | About 3000 |
| Motors | About 150 |
| Electronic tubes | About 2000 |
Besides the function tables for putting information into the machine, there are three mechanisms that read punched paper tape. The three tapes are called the A tape, the B tape, and the C tape. From these tapes the machine is set up to solve a problem.
Suppose that we have decided how the machine is to solve a problem. Suppose that we know the number of integrators, adders, gearboxes, [Pg 83] etc., that must be used, and know how their inputs and outputs are to be connected. To carry out the solution, we now have to put the instructions and numbers into the machine.
The A tape contains instructions for connecting shafts in the machine. Each instruction connects a certain output of one type of mechanism (adder, etc.) to a certain input of another type of mechanism. When the machine reads an instruction on this tape, it connects electrically the transmitting angle-indicator of an output shaft to the receiving angle-indicator of another input shaft.
Now the connecting part of the differential analyzer behaves as if it were very intelligent: it assigns an adder or an integrator or a gearbox, etc., to a new problem only if that mechanism is not busy. For example, if a problem tape calls for adder 3 (in the list belonging to the problem), the machine will assign the first adder that is not busy, perhaps adder 14 (in the machine), to do the work. Each time that adder 3 (in the problem list) is called for in the A tape, the machine remembers that adder 14 was chosen and assigns it over again. This ability, of course, is very useful.
The B tape contains the ratios at which the gearboxes are to be set. For example, suppose that we want gearbox 4 (in the problem list) to change its input by the ratio of 0.2573. The machine, after reading the A tape, has assigned gearbox 11 (in the machine list). Then, when the machine reads the B tape, it sets the ratio in gearbox 11 to 0.2573.
The answer to a differential equation is different for different starting conditions. For example, when we know speed and time and wish to find distance traveled and where we have arrived, we must know the point at which we started. We therefore need to arrange the machine so that we can put in different starting conditions (or different initial conditions, as the mathematician calls them).
The C tape puts the initial conditions into the machine. For example, reading the C tape for the problem, the machine finds that 3000 should, at the start of the problem, stand in counter 4. The machine then reads the number at which counter 4 actually stands, say 6728.3. It subtracts the two numbers and remembers the difference, [Pg 84] -3728.3. And whenever the machine reads that counter later, finding, say, 9468.4 in it, first the 3728.3 is subtracted, and then the answer 5740.1 is printed.
Information may come out of the machine in either one of two ways: in printed numbers or in a graph. In fact, the same quantity may come out of the machine in both ways at the same time. To obtain a graph, we change a function table from input to output, put a pen on it, and have it draw the graph.
The machine has 3 electric typewriters. The machine will take numerical information out of the counters at high speed even while they are turning, and it will put the information into relays. Then it will read from the relays into the typewriter keys one by one while they type from left to right across the page.
Up to this point in this chapter, the author has tried to tell the story of the differential analyzer in plain words. But for reading this section, a little knowledge of calculus is necessary. (See also Supplement 2.) If you wish, skip this section, and go on to the next one.
We have described how varying quantities, or variables, are operated on in the machine in one way or another: adding, subtracting, multiplying by a constant, referring to a table, and integrating. What do we do if we wish to multiply 2 variables together? A neat trick is to use the formula:
| xy = | ∫ x dy + | ∫ y dx |
To multiply in this way requires 2 integrators and 1 adder. The connections that are made between them are as follows:
| Shaft x | To Integrator 1, Screw |
| Shaft x | To Integrator 2, Disc |
| Shaft y | To Integrator 1, Disc |
| Shaft y | To Integrator 2, Screw |
| Integrator 1, Wheel | To Adder 1, Input 1 |
| Integrator 2, Wheel | To Adder 1, Input 2 |
| Adder 1, Output | To Shaft expressing xy |
[Pg 85] A product of 2 variables under the integral sign can be obtained a little more easily, because of the curious powers of the differential analyzer. Thus, if it is desired to obtain ∫ xy dt, we can use the formula:
| xy dt = | x d | y dt |
and this operation does not require an adder. The connections are as follows:
| Shaft t | To Integrator 1, Disc |
| Shaft y | To Integrator 1, Screw |
| Integrator 1, Wheel | To Integrator 2, Disc |
| Shaft x | To Integrator 2, Screw |
| Integrator 2, Wheel | To Shaft expressing ∫xy dt |
In order to get the quotient of 2 variables, x/y, we can use some more tricks. First, the reciprocal 1/y can be obtained by using the two simultaneous equations:
| 1 | dy = log y, | ||
| y | |||
| - | 1 | d(log y) = y | |
| y |
The connections are as follows:
| Shaft y | To Integrator 1, Disc and to Integrator 2, Wheel |
| Shaft log y | To Integrator 1, Wheel and to Integrator 2, Disc |
| Shaft 1/y | To Integrator 1, Screw, and negatively to Integrator 2, Screw |
In order to get x/y, we can then multiply x by 1/y. We see that this setup gives us log y for nothing, that is, without needing more integrators or other equipment. Clearly, other tricks like this will give sin x, cos x, eˣ, x², and other functions that satisfy simple differential equations.
An integral of a reciprocal can be obtained even more directly. Suppose that
| y = | 1 | dt | |
| x |
Then
| Dₜ y = | 1 | , Dy t = x, |
| x |
| t = | x dy |
The connections therefore are:
| Shaft t | To Integrator, Wheel |
| Shaft x | To Integrator, Screw |
| Shaft y | To Integrator, Disc |
[Pg 86] The light wheel then drives the heavy disc. Clearly only the angle-indicator device makes this possible at all. Naturally, the closer the wheel gets to the center of the disc, that is, x approaching zero, the greater the strain on the mechanism, and the more likely the result is to be off. Mathematically, of course, the limit of 1/x as x approaches zero equals infinity, and this gives trouble in the machine.
There is no standard mathematical method for solving any differential equation. But the machine provides a standard direct method for solving all differential equations with only one independent variable. First: assign a shaft for each term that appears in the equation. For example, the highest derivative that appears and the independent variable are both assigned shafts. The integral of the highest derivative is easily obtained, and the integral of that integral, etc. Second: connect the shafts so that all the mathematical relations are expressed. Both explicit and implicit equations may be expressed. Third: for any shaft there must be just one drive, or source of torque. A shaft may, however, drive more than one other shaft. Fourth: choose scale factors so that the limits of the machine are not exceeded yet at the same time are well used. For example, the most that an integrator or a function table can move is 1 or 2 feet. Also, the number of full turns made by a shaft in representing its variable should be large, often between 1000 and 10,000.
Of course, as with all these large machines, anyone would need some months of actual practice before he could put on a problem and get an answer efficiently.
The second MIT differential analyzer is probably the best machine ever built for solving most differential equations. It regularly has an accuracy of 1 part in 10,000. This is enough for most engineering problems. If greater accuracy is needed, the second differential analyzer cannot provide it. Once in a while the machine can reach an accuracy of 1 part in 50,000; but, to balance this, it is sometimes less accurate than 1 part in 10,000. [Pg 87]
The MIT differential analyzer No. 2 can find answers to problems very quickly. The time for setting up a problem to be run on the machine ranges from 5 to 15 minutes. The time for preparing the tapes that set up the problem is, of course, longer; but the punch for preparing the tape is a separate machine and does not delay the differential analyzer. The time for the machine to produce a single solution to a problem ranges usually from 3 minutes to a half-hour. It is easy to put on a problem, run a few solutions, take the problem off, study the results, change a few numbers, and then put the problem back on again. This virtue is a great help in a search in a new field. While the study is going on, time is not wasted, for the machine can be busy with a different problem.
Running a problem a second time is a good check on the reliability of an answer. For, when the problem is run the second time, we can arrange that the machine will route the problem to other mechanisms.
The machine has a control panel. Here the operator watching the machine can tell what units are doing what parts of what problems. If a unit gives trouble or needs to be inspected, the clerk can throw a “busy” switch. Then the machine cannot choose that unit for work to be done. The machine contains many protecting signals and alarms. It is idle for repairs less than 5 per cent of the time.
It is not easy to determine the total cost of the machine, for it was partially financed by several large gifts. Also, much of the labor was done by graduate students in return for the instruction that they gained. The actual out-of-pocket cost was about $125,000. If the machine were to be built by industry, the cost would likely be more than 4 times as much. A simple differential analyzer, however, can be cheap. Small scale differential analyzers have been built for less than $1000; their accuracy has been about 1 part in 100.
There are many things that this machine cannot do; it was not built to do them. (1) It cannot choose methods of solution. (2) It cannot perform steps in solving a problem that depend on results as they are found. (3) It cannot solve differential equations containing two or more independent variables. Such equations are called partial [Pg 88] differential equations; they appear in connection with the flow of heat or air or electricity in 2 or 3 dimensions, and elsewhere. (4) It cannot solve problems requiring 6 or more digits of accuracy. (5) The machine, while running, can store numbers only for an instant, since it operates on the principle of smoothly changing quantities; however, when the machine stops, the number last held by each device is permanently stored.
None of these comments, however, are criticisms of the machine. Instead they show avenues of development for future machines. As was said before, for solving most differential equations, this machine has no equal to date. The range of problems which any differential analyzer can do depends mostly on the number of its integrators. The second differential analyzer has 18 and provides for expansion to 30. The machine is constructed, also, so that it can be operated in 3 independent sections, each working to solve a different problem. The differential analyzer can operate unattended. After it has been set up and the first few results examined, it can be left alone to grind out large blocks of answers.
An interesting example of the experimental use of a differential analyzer in a commercial business is the following: In Great Britain, R. E. Beard of the Pearl Assurance Company built a differential analyzer with 6 integrators. He applied this machine to compute to 3 figures certain insurance values known as continuous annuities and continuous contingent insurances. He has described the machine and the application he made in a paper published in the Journal of the Institute of Actuaries, Vol. 71, 1942, pp. 193-227.
[Pg 89]
One of the first giant brains to be finished was the machine in the Computation Laboratory at Harvard University called the IBM Automatic Sequence-Controlled Calculator. This great mechanical brain started work in April 1944 and has been running 24 hours a day almost all the time ever since. It has produced quantities of information for the United States Navy. Although many problems that have been placed on it have been classified by the Navy as confidential, the machine itself is fully public. The way it was working on Sept. 1, 1945, has been thoroughly described in a 540-page book published in 1946, Volume I of the Annals of the Harvard Computation Laboratory, entitled Manual of Operation of the Automatic Sequence-Controlled Calculator. Since then the machine has been improved in many ways.
This machine does thousands of calculating steps, one after another, according to a scheme fixed ahead of time. This property is what gives the machine its name: automatic, since the individual operations are automatic, once the punched tape fixing the chain of operations has been put on the machine, and sequence-controlled, since control over the sequence of its operations has been built into the machine.
More than a hundred years ago, an English mathematician and actuary, [Pg 90] Charles Babbage (1792-1871), designed a machine—or engine as he called it—that would carry out the sequences of mathematical operations. In the 1830’s he received a government grant to build an analytical engine whereby long chains of calculations could be performed. But he was unsuccessful, because the refined physical devices necessary for quantities of digital calculation were not yet developed. Only in the 1930’s did these physical devices become sufficiently versatile and reliable for a calculator of hundreds of thousands of parts to be successful.
The Automatic Sequence-Controlled Calculator at Harvard was largely the concept of Professor Howard H. Aiken of Harvard. It was built through a partnership of efforts, ideas, and engineering between him and the International Business Machines Corporation, in the years 1937 to 1944. The calculator was a gift from IBM to Harvard University. Some very useful additional control units, named the Subsidiary Sequence Mechanism, were built at the Harvard Computation Laboratory in 1947 and joined to the machine.

Fig. 1. Scheme of Harvard IBM Automatic
Sequence-Controlled Calculator.
The machine (see Fig. 1) is about 50 feet long, 8 feet high, and about 2 feet wide. It consists of 22 panels; 17 of them are set in a straight line, and the last 5 are at the rear of the machine. In the scheme of the machine shown in Fig. 1, the details you [Pg 91] would see in a photograph have been left out. Instead you see the sections of the machine that are important because of what they do: input, memory, control, and output. Why do we not see a section labeled “computer”? Because in this mechanical brain the computing part of the machine is closely joined to the memory: every storage register can add and subtract. We shall soon discuss these sections of the machine more fully.
Now in order for any brain to work, physical devices must be used. For example, in the human body, a nerve is the physical device that carries information from one part of the body to another. In the Harvard machine, an insulated wire is the physical device that carries information from one part of the machine to another. One side of every panel in the Harvard machine is heavily laden with a great network of wires. Between the panels, you can see in many places cables as thick as your arm and containing hundreds of wires. More than 500 miles of wire are used.
The physical devices in the Harvard machine are numerous, as we would expect. It is perhaps not surprising that this machine has more than 760,000 parts. But, curiously enough, there are only 7 main kinds of physical devices in the major part of the machine. They are: wire, two-position switches, two-position relays (see Chapter 2), ten-position switches, ten-position relays, buttons, and cam contacts (see below). These are the devices that handle information in the form of electrical impulses. They can be combined by electrical circuits in a great variety of ways. There are, of course, other kinds of physical devices that are important, but they are not numerous, and they have rather simple duties. Looking at the machine, you can see three examples easily. Physical devices of the first kind convert punched holes into electrical impulses: 2 card feeds, 4 tape feeds. Those of the second kind convert electrical impulses into punched holes: 1 card punch, 1 tape punch. Those of the third kind convert electrical impulses into printed characters: 2 electric typewriters. We can think of a fourth kind of physical device that [Pg 92] would be a help, but, at present writing, it does not yet exist: a device that converts printed characters into electrical impulses.
The Harvard machine, of course, is complicated. But it is complicated because of the variety of ways in which relatively simple devices have been connected together to make a machine that thinks.
A two-position switch (see Fig. 2) turned by hand connects a wire to either one of 2 others. These 2 positions may stand for “yes” and “no,” 0 and 1, etc. There are many two-position switches in the machine. A ten-position switch or dial switch (see Fig. 3) turned by hand connects the wire running into the center of the switch with a wire at any one of ten positions 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 around the edge. There are over 1400 dial switches in the machine. How does turning the pointer on the top of the dial make connection between the center wire and the edge wire? Under the face of the dial is the part that works, a short rod of metal fastened to the pointer (shown with dashes in Fig. 3). When the pointer turns, this rod also turns, making the desired connection.

Fig. 2.Two-position switch.
Fig. 3. Dial switch.
Two-position relays—more often called just relays (see Chapter 2)—do the automatic routing of the electrical impulses that cause computing to take place. Each relay may take 2 positions, open or closed, and these positions may stand for 0 and 1. There are more than 3000 relays in the Harvard machine.
A magnet pulling one way and a spring pulling the other way are sufficient in an ordinary relay to give 2 positions, “on” and “off,” “yes” and “no,” 0 and 1. But how do we make a relay that can hold any [Pg 93] one of 10 positions? Figure 4 shows one scheme for a ten-position relay. The arm can take any one of 10 positions, connecting the contact Common to any one of the contacts O, 1, 2, 3, 4, 5, 6, 7, 8, and 9 so that current can flow. The gear turns all the time. When an impulse comes in on the Pickup line, the clutch connects the arm to the gear. When an impulse comes in on the Drop-out line, the clutch disconnects the arm from the gear. For example, suppose that the ten-position relay is stopped at contact 2, as shown. Suppose that we now pick up the relay, hold it just long enough to turn 3 steps, and then drop it out. The relay will now rest at contact 5.
Fig. 4. Scheme of a ten-position relay,
or counter position.
Fig. 5. Scheme of a
counter wheel.
In the Harvard machine, the ten-position relays, much like the scheme shown, do the same work as counter wheels (Fig. 5) in an ordinary desk calculating machine, and so they are often spoken of as counter positions in the Harvard machine. They are very useful in the machine not only because they express the 10 decimal digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 but also because adding and subtracting numbers is accomplished by turning them through the proper number of steps. In fact, an additional impulse is provided when the counter position turns from 9 to 0, for purposes of carry. A group of 24 counter positions makes up each storage counter—or storage register—in the machine. There are 2200 of these counter positions. Each is connected to a continuously running gear on a small shaft (Fig. 6). All these shafts are connected by other gears and shafts to a main drive shaft, and they are driven by a 5-horsepower motor at the back of the machine. When a counter position is supposed [Pg 94] to step, a clutch connects the drive to the running gear, and the counter position steps. When the counter position is supposed to stay unchanged, the clutch is disconnected and the driving gear runs free. In fact, when you first approach the Harvard machine, about the first thing you are aware of is the running of these gears and the intermittent whirring and clicking of the counter positions as they step. The machine gives a fine impression of being busy!
Fig. 6. Scheme of counter 16.
A button (see Fig. 7) is a device for closing an electric circuit when and only when you push it. A simple example is the button for ringing a bell: you push the button, a circuit is closed, and something happens. When you let go, the circuit is opened. The Harvard machine has a button for starting, a button for stopping, and many others.
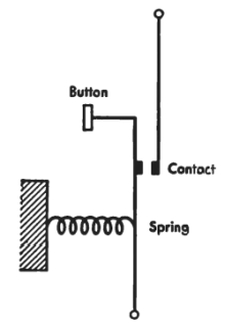
Fig. 7. Button.
Fig. 8. Cam, with 5 lobes and contact.
[Pg 95] A cam contact (see Fig. 8) is an automatic device for closing an electric circuit for just a short interval of time. When the lobes on the cam strike the contact, it closes and current flows. When the lobes have gone by, the spring pushes open the contact, and no current flows. Just as a two-position relay is the automatic equivalent of a two-position switch, and a ten-position relay is the automatic equivalent of a ten-position switch, so a cam contact is the automatic equivalent of a button.
All the cams in the machine have 20 pockets where small round metal lobes may or may not be inserted. Each cam makes a full turn once in ³/₁₀ of a second and is in time with all the others. Thus we can time all the electrical circuits in the machine in units of ³/₂₀₀ of a second.
Numbers in the machine regularly consist of 23 decimal digits. The 24th numerical position at the left in any register contains only 0 for a positive number and only 9 for a negative number. Nines complements (see Supplement 2) are used for negative numbers. For example,-00284 is represented as 999715, supposing that we had 5-digit numbers instead of 23-digit numbers. The sum of two nines complements is automatically corrected so that it is still a correct nines complement. The device that accomplishes this is called end-around-carry (see Supplement 2). The decimal point is fixed for each problem; in other words, in any problem, the decimal point is consistently kept in one place, usually between the 15th and 16th decimal columns from the right.
Numerical information may go into the machine in any one of 3 ways: (1) by regular IBM punch cards, using standard IBM card feeds (panel 16); (2) by hand-set dial switches (panels 1, 2); and (3) by long loops of punched tape placed on the value tape feeds (panels 12 to 14). Three sets of 24 columns each punched on a regular IBM punch card can be used to send 3 numbers and their signs into the machine in one machine cycle. [Pg 96] This is the fastest way for giving numbers to the machine, but the most limited; for the cards must be referred to in order and can be referred to automatically only once. Also, there is the risk that they may be out of order. A card may be passed through the machine without reading; this saves some sorting in preparing cards for the machine. Machines for preparing the cards are regular IBM key punches, and machines for sorting them after preparation are regular IBM card sorters.
In panels 1 and 2 there are 60 registers by which unchanging numbers like 1, or 3.14159265···, or 7.65 may be put into the machine. These are called the constant registers. Each constant register consists of 24 dial switches and contains 23 digits and a sign, 0 if positive and 9 if negative. Whenever the mathematician says a certain constant is needed for a problem, the operator of the machine walks over to these panels, and, while the machine is turned off, sets the dial switches for the number, one by one, by hand. If we need 40 constants of 10 digits each for a problem, then the operator sets 400 dial switches by hand and makes certain that the remaining 14 switches in each of the 40 constant registers used are either at 0 or 9, depending on the sign of the number. Only then can he return to start the machine.
Fig. 9. Value tape code.
The third means by which numerical information can be put into the machine is the value tape feeds, in panels 12, 13, and 14. Here the machine can consult tables of numbers. The numbers are punched on paper tape 24 holes wide, made of punch-card stock. Tapes for the value tape feeds may be prepared by hand or by the machine itself using punch cards or machine calculation. The tapes use equally spaced arguments (see Supplement 2). The tape punch changes the decimal digits in its keyboard into the following punching code (see Fig. 9):
| 0 | 0000 | 5 | 1100 | |
| 1 | 1000 | 6 | 1010 | |
| 2 | 0010 | 7 | 1001 | |
| 3 | 0010 | 8 | 0110 | |
| 4 | 0001 | 9 | 0101 |
[Pg 97] Here the 1 denotes a punched hole and 0 no punched hole, and the 4 columns from left to right of the code correspond to 4 rows of the paper tape from bottom to top. To make sure the value tape is correct, the machine itself can read the value tape and check it mathematically or compare it with punch-card values.
Information comes out of the machine in any one of three ways: (1) by punching on IBM cards with a regular IBM card punch that is built into the machine (panel 17), (2) by typing on paper sheets with electric typewriters (panels 16 and 17), and (3) by punching paper tape 24 holes wide of the same kind as is fed into the machine.
Usually, one of the electric typewriters is used to print a result for a visual check and to print it before the machine makes a specified check of the value. Then, about 10 seconds later, after the result has been checked as specified in the machine, the checked result is printed by the second typewriter. In the second typewriter, a special one-use carbon ribbon of paper is used to produce copy for publication by a photographic process.
The card punch writes a number more rapidly than an electric typewriter. This extra speed is sometimes very useful. However, the punch’s chief purpose is to record intermediate results on punch cards. Then, if there is a machine failure, and if the problem has been well organized, the problem may be run over from these intermediate results, instead of requiring a return to the original starting information. The tape punch used for preparing tape by hand can also be operated by cable from the machine.
The machine is a mechanical brain. So, between taking in information and putting out information, the machine does some “thinking.” It does this thinking according to instructions. The instructions go into the machine as: (1) the setting of switches, or (2) the pressing of buttons, or (3) the wiring of plugboards, or (4) feeding in tape [Pg 98] punched with holes. The instructions are remembered in the machine in these 4 ways, and we can call these sets of devices the control of the machine.
To illustrate: One of the buttons pressed for every problem is the Start Key: when you press it, the machine starts to work on the problem. One of the switches with which you give instructions is a switch that turns electric typewriter 1 on or off. One of the plugboards contains some hubs by which you can tell the machine how many figures to choose in the quotient when dividing, for clearly you do not need a quotient of 23 figures every time the machine divides. You can have 5 choices in any one problem; you can specify them by plugging, and you can call for any one of 5 choices of quotient size from time to time during the problem. In many cases, when we wish the machine to do the same thing for all of a single problem and do it whenever the occasion arises, we can put the instruction into the wiring of a plugboard. We use plugboard wiring, for example, in fixing the decimal point in multiplication, so that the product will read out properly, and in guiding the operation of the typewriters, so that printing will take place in the columns where we want it.
The most important part of the control of the machine is the sequence-tape feed and its sequence-control tape. These tell the machine a great part of what operations are to be performed.
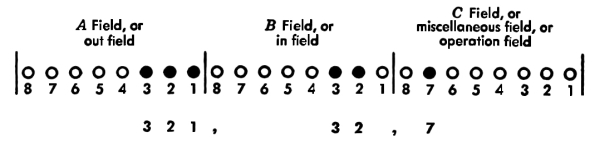
Fig. 10. Sequence-control tape code.
At the end of the room where the machine is, there is the special tape punch mentioned above. It holds a big spool of card stock that is thin, flexible, smooth, and tough. With one keyboard we may prepare value tape. With another keyboard we prepare the sequence-control tape. The tape (see Fig. 10) contains places for 24 round punched holes in each row. Some and only some of these holes are punched. Each row of punched [Pg 99] holes is equivalent to an instruction to the machine and is called a line of coding or coding line. In general, the instruction has the form:
The first group of 8 holes at the left is called the A field or the out-field. Here we tell the machine where a number is to be taken from. The middle group of 8 holes is called the B field or the in-field. Here we tell the machine where a number is to be put. The last group of 8 holes is called the C field or the miscellaneous field. Here we tell the machine part or all of the operation that is to be performed.
To illustrate (see Fig. 10), we have holes 3, 2, 1 punched in the A field, holes 3, 2 punched in the B field, and hole 7 punched in the C field. Now 321 is the code—or machine language, or machine call number—for storage counter 7; 32 is the code for storage counter 6; and 7 in the C field is the code (in this case, and generally) for “Add, and read the next line of coding.” So, if we punch out this line of coding and put the tape on the machine, we tell the machine to read the number in counter 7, add it into counter 6, and proceed to the next line of coding and read that.
The holes in each group of 8 holes from left to right are numbered: 8, 7, 6, 5, 4, 3, 2, 1. The code 631, for example, means that holes 6, 3, 1 are punched and that no holes are punched at 8, 7, 5, 4, 2. Since it is more natural, the code is read from left to right, or 631, instead of from right to left in the sequence 136.
The devices in the machine have in-codes, used in the in-field, and out-codes, used in the out-field. For each of the 72 regular storage counters, the in-code and the out-code are the same. The first 8 storage counters have the codes 1, 2, 21, 3, 31, 32, 321, 4, 41; the last 2 storage counters, the 71st and the 72nd, have the codes 7321, 74.
The constant registers—often called constant switches, or just switches—naturally have only out-codes, since numbers can be entered into the constant registers only by setting dial switches by [Pg 100] hand. The first 8 constant registers have the out-codes 741, 742, 7421, 743, 7431, 7432, 74321, 75, and the 59th and 60th constant registers have the out-codes 821, 83.
Each storage counter has the property that any number transferred into it is added into it. For example, the instruction
is coded:
741, 321, 7
The 7 in the third column is an instruction to the sequence-tape feed to turn up to the next coding line and read it. If any number is already stored in register 321, the content of 741 will be added to it, and the total will then be stored in 321.
Resetting or clearing a regular storage register is accomplished by a coding that is a departure from the usual scheme of “out” and “in.” The instruction
is coded:
321, 321, 7
Similarly, you can clear any other regular storage register if you repeat its code in the out-and in-fields. However, a few of the storage registers in the machine have special reset codes, and these may occur in any of the three fields A, B, C.
As the result of a recent modification of the machine, you can easily double the number in any storage register. For example, the instruction
is coded:
321, 321, 743
If the number in switch 741 is to be subtracted from the number in storage counter 321, the instruction is changed into:
[Pg 101] The coding line becomes:
741, 321, 732
By putting 32 in the C field, we cause the number in switch 741 to be subtracted from whatever number is in register 321.
We have 2 more choices in adding and subtracting. The value of the number without regard to sign—in other words, its absolute value (see Supplement 2)—may be added or subtracted. The instruction
Add the absolute value of
is expressed by a C field code 2, and the instruction
Add the negative of the absolute value of
is expressed by a C field code 1.
When we wish to multiply one number by another and get a product, we have 3 numbers. We tell the machine about each of these numbers on a separate line of coding. Multiplication is signaled by sending a number into the multiplicand counter. The multiplicand counter has an in-code 761. If the multiplicand is in 321, the instruction is:
The coding is:
321, 761, 7
On the third following coding line, the multiplier is sent into the multiplier counter. If the multiplier is in switch 741, the instruction is:
The coding is:
741, ——, 7
We do not punch anything in the middle field: the machine is “educated” and “knows” that it has started a multiplication and needs a [Pg 102] multiplier, and it expects this multiplier in the third coding line. To have no code for the multiplier counter is, of course, a departure from the general rule, but it saves some punching and permits the use of this space for certain other codes, thus saving some operating time.
We need not confuse the 761 in-code for the multiplicand counter with the 761 out-code, which happens to be the out-code of the 25th constant register, because neither can occur in the other’s field. We may, of course, use other registers besides 321 and 741 for supplying the multiplicand and multiplier.
To get the product and put it into any storage counter D, we use two lines of coding one right after the other:
—— —— 6421
8761 D ——
The product counter has the out-code 8761. When the product is desired, it is called for, transferred into counter D, and the multiplication unit is automatically cleared. It takes time, however, for the machine to perform a multiplication. That is the reason for the preceding coding line and the 6421 in the C field. While the multiplication is going on, we can instruct the machine to do other things that we want done. We can insert or interpose coding lines in between the multiplier line and the product line. For example, if we have a multiplier of 10 digits, we can insert 8 coding lines and maybe more. The 6421 code essentially tells the machine to finish both the multiplication and the interposed instructions, and, as soon as the later one of these two tasks is finished, to transfer out the product to counter D.
Up to the middle of 1946, the wiring of the machine was a little different and less convenient. When the product was obtained by the multiplication unit, it had to be accepted and transferred at once into one of the 72 storage registers.
Division is called for by first sending the divisor into the divisor counter, and this has a code 76 in the B field. If the divisor is in counter 321, the instruction may be:
[Pg 103] The coding will then be:
321, 76, 7
Three coding lines later, the dividend is called for, and the coding, if the dividend is in switch 7431, is:
7431, ——, 7
We can send the quotient, when ready, into any desired counter Q by the following two lines of coding:
—— —— 642
876 Q ——
In the same way as with multiplication, we can insert a number of coding lines in between the dividend line and the first quotient line.
Both multiplication and division are carried out in the same unit of the machine, the multiply-divide unit. The machine first constructs a table of the multiples of the multiplicand or divisor: 1 times, 2 times, 3 times, ···, 9 times. In multiplication this table is then used by selecting multiples according to the digits of the multiplier one after another. In division the table is used by comparing multiples of the divisor against the dividend and successive remainders, finding which will go and which will not. Since the numbers in the machine are normally of 15 to 23 digits, any particular multiple will be used, on the average, several times, and so this process is relatively efficient. Actually the multiplicand and the divisor go into the same counter. Division, however, has the code 76 and multiplication the code 761, and so the difference is essentially an operation code not in the third or C field.
When we desire the machine to consult a table of values (i.e., a function—see Supplement 2), we punch the table with its arguments and function values on a tape, and we put the tape on a value tape feed mechanism. The instruction to the machine may be:
[Pg 104] The coding is:
| —— | —— | 73 |
| A | 7654 | 61 |
| —— | —— | 762 |
| —— | —— | 543 |
| —— | —— | 75431 |
| 841 | 7654 | —— |
| A | 763 | 6421 |
| 8762 | B | 73 |
| —— | 8763 | 7 |
Without explaining this coding line by line, we can say that this is what happens:
The machine reads the argument in register A. The machine reads the argument in the table at which the value tape feed is resting.
It subtracts them, and thereby determines how far away the desired argument is.
The machine then turns the tape that required distance.
It checks that the new argument is the wanted argument.
It reads the value of the function entered at that point on the function tape.
There is a storage counter in the machine that is called the selection counter. The selection counter is counter 70 and has the code 732. It has all the properties of an ordinary storage counter and, in addition, one extra property: depending on the sign of the number stored in the selection counter, it is possible to select whether some other number shall be treated positively or negatively. In other words, addition of a number anywhere in the machine may take place either positively or negatively, if the number stored in the selection counter is positive or negative, respectively.
For example, suppose that x is the number in the selection counter. Suppose that y is the number in some other counter A. Suppose that z is the number in counter B. Suppose that we use the coding:
A, B, 7432
[Pg 105] What we get in B, because of the 7432 in the third or C field, is z plus y if x is positive or zero, and z minus y if x is negative. In the language of the algebra of logic (see Chapter 9 and Supplement 2), where T( ...) is “the truth value of ...,” the number in b equals:
z + y·T(x ≥ 0) - y·T(x < 0)
(The nines complement of 0, namely 999···9 to 24 digits, is treated by the machine as negative.)
Why do we need an operation like this in a mechanical brain? Among other reasons, what we want to do with a number, in mathematics, often depends on its sign. It may happen that a table is, for negative arguments, the negative of what it is for positive arguments; in other words, F(-x) =-F(x). This is true, for instance, for a table of cubes {F(x) = x³} or for a table of trigonometric tangents (see Supplement 2). If so, we certainly do not want to take the time and trouble to list the whole table. We put down only half the table and then, if x is negative, use the negative of the value in the table. In order to apply such a time-saving rule when using the machine, we need the selection counter or its equivalent.
There is another special counter in the machine that is called the check counter. It also has all the properties of an ordinary storage counter and, in addition, one extra property: If the sign of the number stored in the check counter on a certain coding line is negative, then on the next coding line the machine may be stopped. In other words, suppose that the check counter stores a certain tolerance t. Suppose, under the instructions we give the machine, that it calculates a positive number x that ought to be less than this tolerance. Suppose that something may go wrong and that x actually may be greater than t. Then we put a check into our instructions. We tell the machine:
[Pg 106] Here is the coding. Suppose that the tolerance t is in switch 751. Suppose that the number x to be checked is in counter 4321. Then the instructions and coding are:
| Clear the check counter | — | — | 7 |
| Put in the tolerance, from switch 751 | 751 | 74 | 7 |
| Subtract the absolute value of the number to be checked | 4321 | 74 | 71 |
| Stop, O Mechanical Brain, if your result be negative! | — | — | 64 |
An operation like this is very useful in a mechanical brain. It enables the calculation to be interrupted if something has gone wrong. Of course, other operations of checking besides this one are used—for example, inspecting for reasonableness the results printed on typewriter 1.
There are other operations in the machine. There are two pairs of storage registers that can be coupled together so that we can handle problems requiring numbers of 46 digits instead of 23. Registers 64 and 65 can be coupled, and registers 68 and 69 can be coupled. There is another storage counter, No. 71, that has an extra property. We can read out the number it holds times 1, or times 10¹², or times 10⁻¹², as may be called for. As a result of this counter, we can do problems requiring 144 registers storing numbers of 11 digits each, instead of 72 registers storing 23 digits each. Bigger statistical problems can be handled, for example.
There are some minor sequences of operations, or subroutines, that can be called for by a single code. The subroutine may be a whole set of additions, subtractions, multiplications, divisions, and choices, having a single purpose: to compute some number by a process of rapid approximation (see Supplement 2). There are built-in subroutines for some special mathematical functions: the logarithm of a number to the base 10, the exponential of a number to the base 10, and the sine of a number. (See Supplement 2.)
There are also 10 changeable subroutines, each of 22 coding lines, which can be called in, when wanted, by the main sequence-control tape or by each other. These subroutines constitute the Subsidiary Sequence [Pg 107] Mechanism, and are extremely useful. They have A, B, and C fields just like the main sequence-control, but they are given information by plugging with short lengths of wire instead of by feeding punched paper tape.
Up to this point in this chapter the author has tried to tell the facts about the Harvard machine in plain words. But for reading this section, a little knowledge of calculus is necessary. (See also Supplement 2.) If you wish, skip this section and go on to the next one.
What is the process that the machine uses to compute any desired logarithm to 23 digits? Suppose that we take for an example the process by which the machine computes log10 49.3724. We choose a 6-digit number for simplicity; the machine would handle a 23-digit number in the same way. The process uses 2 fundamental equations involving the logarithm: the sum relation
log (a·b·c···) = log a + log b + log c···
and the series relation
| logₑ(1 + h) = h - | h² | + | h³ | - | h⁴ | + ···, │h│ < 1 |
| 2 | 3 | 4 |
The error in this series is less than the first neglected term. Now, the machine stores the base 10 logarithms (to 23 decimal places) of the following 36 numbers:
| 1 | 1.1 | 1.01 | 1.001 |
| 2 | 1.2 | 1.02 | 1.002 |
| ... | ... | ... | ... |
| 9 | 1.9 | 1.09 | 1.009 |
First, the number 49.3724 is examined in a counter called the Logarithm-In-Out counter, and the position of the decimal point is determined, giving the characteristic of the logarithm. The number 49.3724 has the characteristic 1. Next, 4 successive divisions are performed, in which the 4 divisors are (1) the first digit of the number, (2) the first 2 digits of the quotient, (3) the first 3 digits of the next quotient, and (4) the first 4 digits of the subsequent quotient; thus, [Pg 108]
| 4.93724 | = 1.23431 |
| 4 | |
| 1.23431 | = 1.02860 |
| 1.2 | |
| 1.02860 | = 1.00843 |
| 1.02 | |
| 1.00843 | = 1.00043 |
| 1.008 |
For simplicity we have kept only 6 digits, although the machine, of course, would keep 23. It is interesting to note that the machine is able to sense digits and thus determine the 4 divisors; this is an arithmetical and numerical process and one that cannot be done in ordinary algebra. We now have:
log₁₀ 49.3724 = 1 + log₁₀ 4 + log₁₀ 1.2 + log₁₀ 1.02
+ log₁₀ 1.008 + log₁₀ 1.00043
To compute log₁₀ 1.00043 to 21 decimals we use
| log₁₀e · | h - | h² | + | h³ | - | h⁴ | + | h⁵ | - | h⁶ | ||
| 2 | 3 | 4 | 5 | 6 |
with h = 0.00043. Only 6 terms of the series relation are needed. For, the error is less than h⁷/7, which is less than 10⁻²¹/7, since h < ¹/₁₀₀₀. The machine uses the series relation in the form
log₁₀ (1 + h) = {([{(c₆h + c₅) h + c₄}h + c₃]h + c₂)h + c₁}h
where
c₁ = M, c₂ = -M/2, c₃ = M/3, ···,
and M = log₁₀_e= 0.434294···.
The 6 values of the c’s are also stored in the machine. When any logarithm is to be computed, the sum of the characteristic, of the 4 logarithms of the successive divisors, and of the first 6 terms of the series relation gives the logarithm. The maximum time required is 90 seconds.
The IBM Automatic Sequence-Controlled Calculator at Harvard is a [Pg 109] landmark in the development of machines that think. Its capacity for many problems for which it is suited is far beyond the capacity of a hundred human computers.
The time required in the machine for adding, subtracting, transferring, or clearing numbers is ³/₁₀ of a second. This is the time of one machine cycle or of reading one coding line. Multiplication takes at the most 6 seconds, and an average of 4 seconds. Division takes at the most 16 seconds, and an average of 11 seconds. Each, however, requires only 3 lines of coding, or ⁹/₁₀ of a second’s attention from the sequence mechanism; interposed operations fill the rest of the time. To calculate a logarithm, an exponential, or a sine to the full number of digits obtainable by means of the automatic subroutine takes at the most 90, 66, and 60 seconds, respectively. To get three 24-digit numbers from feeding a punch card takes ⅓ second. To punch a number takes from ½ second up to 3 seconds. To print a number takes from 1½ seconds up to 7 seconds.
The cost of the machine was somewhere near 3 or 4 hundred thousand dollars, if we leave out some of the cost of research and development, which would have been done whether or not this particular machine had ever been built. A staff of 10 men, consisting of 4 mathematicians, 4 operators, and 2 maintenance men, are needed to keep the machine running 24 hours a day. This might represent, if capitalized, another 1 or 2 hundred thousand dollars. If a capital value of $500,000 is taken as equivalent to $50,000 a year, then the cost of the machine in operation 24 hours a day is in the neighborhood of $150 a day or $6 an hour.
The value of the machine, however, is very much greater. If 100 human beings with desk calculators were set to work 8 hours a day at $1.50 an hour, the cost would be $1200 a day, or 8 times as much. Yet it is very doubtful that the work they could produce would equal that turned out by the machine, either in quality or quantity, when the machine is well suited to the problem. [Pg 110]
By reliability we mean the extent to which the results produced by the machine can be relied on to be right. The machine contains no built-in device for making its operations reliable. So, if we wish to check a multiplication, for example, we can do the multiplication a second time, interchanging the multiplier and the multiplicand. But if, say, digit 16 of the product were not transferring correctly, we would get the same wrong result both ways and we would not have a sufficient check. Thus, when we set up a problem for the machine to do, one of the big tasks we have is checking. We have to work out ways of making sure that the result, when we get it, is right and ways of instructing the machine to make the tests we want. This is not a new task. Whenever you or I set out to solve a problem, we have to make sure—usually by doing the problem twice, and preferably by doing it a different way the second time—that our answer, when we get it, is correct. One of the chief tasks for the mathematician, in making a sequence-control tape for the machine, is to put into it sufficient checks to make sure that the results are correct.
We can use a number of different kinds of partial checks: the check counter; differences, and smoothness (see Supplement 2); watching the results printed on typewriter 1; mathematical checks; comparison with known specific values; etc.
In actual experience on the machine, human failures, such as failure to state the problem exactly or failure to put it on the machine correctly, have given about as much trouble as mechanical failures. The machine operates without mechanical failure about 90 to 95 per cent of the time. The balance of the time the machine is idle while being serviced or repaired. The machine is serviced by mechanics trained and supervised at Harvard.
Often when we change the machine from one problem to another problem, we find some kind of trouble. Consequently, we need to work out in detail the first part of any calculation placed on the machine. We then compare the results step by step with the results produced by the machine. Any mathematician working with the machine needs considerable [Pg 111] training in order to diagnose trouble quickly and guide the maintenance men to the place where repair or replacement is needed. Once you find the trouble, you can fix it easily. Without disturbing the soldered connections, you can easily pull out from its socket a relay that is misbehaving and plug in a new relay. With a screwdriver you can change a counter position—detach it from its socket and replace it by another one that is working correctly.
One “bug” that will long be remembered around the Laboratory was a case involving a 5 that would incorrectly come in to a number every now and then. It did not happen often—only once in a while. After a week of search the bug was finally located: the insulation on a wire that carried a 5 had worn through in one spot, and once in a while this wire would shake against a post that could carry current and took in the 5!
In many respects, this machine is efficient and well-balanced. Its reading and writing speed is close to its calculating speed. We can punch or print a result on the average for every 10 additions or 1½ multiplications. The memory of 72 numbers in the machine is extremely useful; a smaller memory is a serious limitation on the achievements of a computing machine. The machine can do many kinds of arithmetic and logic. It is well educated and can compute automatically some rather complicated mathematical functions, like logarithm or sine. It has done difficult and important problems. It has computed and tabulated (see Supplement 2) Bessel functions, definite integrals, etc. It can solve differential equations (see Chapter 5) and many other problems in mathematics, physics, and engineering.
On the other hand, no calculator will ever again be built just like this one, useful though it is. Electronic computing is easily 100 times as fast as relay computing; nearly every future calculator will do its computing electronically. Many other improvements will be made. For example, in this calculator, there are 72 addition-subtraction mechanisms, yet only one of these can be used at a time. Also, the machine has only one combined multiply-divide unit. So we have to [Pg 112] organize any computation with few multiplications, and with still fewer divisions, for they take longer still.
Until 1947, we had to organize any computation in this calculator into one single fixed sequence of operations. In other words, there was no way to move from one subroutine to another subroutine depending on some indication that turned up in our computation. Recently, the Harvard Computation Laboratory decided to remedy this condition and provided the Subsidiary Sequence Mechanism equivalent to 10 subroutines of 22 lines of coding each. These are on relays and plug wires and may be called for by the sequence-control tape or by each other. This provision has added greatly to the efficiency of the calculator.
Whatever else can be said about the Harvard IBM Automatic Sequence-Controlled Calculator, it must be said that this was the first general-purpose mechanical brain using numbers in digit form and able to do arithmetic and logic in hundreds of thousands of steps one after another. And great credit must go to Professor Howard H. Aiken of Harvard and the men of International Business Machines Corporation who made this great mechanical brain come into existence.
[Pg 113]
Another of the giant brains that has begun to work is named ENIAC. This name comes from the initial letters of the full name, Electronic Numerical Integrator and Calculator. Eniac was born in 1942 at the Moore School of Electrical Engineering, of the University of Pennsylvania, in Philadelphia. Eniac’s father was the Ordnance Department of the U. S. Army, which provided the funds to feed and rear the prodigy.
In the short space of four years, Eniac grew to maturity, and in February 1946 he began to earn his own living by electronic thinking. Eniac promptly set several world’s records. He was the first giant brain to use electronic tubes for calculating. He was the first one to reach the speed of 5000 additions a second. He was the first piece of electronic apparatus containing as many as 18,000 electronic tubes all functioning together successfully. As soon as Eniac started thinking, he promptly made relay calculators obsolete from the scientific point of view, for they have a top speed of perhaps 10 additions a second.
At the age of 5, he moved to Maryland at a cost of about $90,000, and his permanent home is now the Ballistic Research Laboratories at the U. S. Army’s Proving Ground at Aberdeen, Md.
In the Department of Terrestrial Magnetism in the Carnegie Institution [Pg 114] of Washington, a great deal of information about the earth is studied. Many kinds of physical observations are there gathered and analyzed: electricity in the atmosphere, magnetism in the earth, and the weather, for example. In 1941, a physicist, Dr. John W. Mauchly, was thinking about the great mass of numerical information they had to handle. He became convinced that much swifter ways of handling these numbers were needed. He was certain electronic devices could be used for computing at very high speeds, yet he found no one busy applying electronics in this field. With hopes of finding some way of developing electronic computing, he joined the staff of the Moore School of Electrical Engineering in the autumn of 1941.
The Moore School in 1934 and 1935 had built a differential analyzer; and, from that time on, the school had made a number of improvements in it. In 1941, with war imminent, the differential analyzer was put hard at work calculating tables for the Army’s Ballistic Research Laboratories. These tables were mostly firing tables, tables of the paths along which projectiles travel when fired—trajectories; obviously, you cannot fire a gun usefully, unless you know how to aim it. The amount of calculation of trajectories was so huge that Dr. Mauchly suggested that a machine using electronic tubes be constructed to calculate them. A good deal of discussion took place between men at the Moore School, men at the Ballistic Research Laboratories, and men from the Ordnance Department in Washington. A contract for research into an electronic trajectory computer was concluded with the Ordnance Department of the U. S. Army. Mauchly and one of the young electronics engineers studying at Moore School, J. Presper Eckert, Jr., set to work on the design.
Gradually the design of a machine took form, and the crucial experiments on equipment were completed. In 1943, the design was settled as a special-purpose machine to calculate trajectories. Later on, the group modified the plans here and there to enable the machine to calculate a very wide class of problems. A group of Moore School electronics engineers and technicians during 1944 and 1945 built the machine, using as much as possible standard radio tubes and parts. Here, again, in spite of the successful progress of the electronic machine, the rumor that it was a “white elephant” was allowed to spread in order to protect the work from prying enemy ears. [Pg 115]
The main part of Eniac consists of 42 panels, which are placed along the sides of a square U. Each of these panels is 9 feet high, 2 feet wide, and 1 foot thick. They are of sheet steel, painted black, with switches, lights, etc., mounted on them. At the tops of all the panels are air ducts for drawing off the hot air around the tubes. Large motors and fans above the machine suck the heated air away through the ducts. There are also 5 pieces of equipment which can be rolled from place to place and are called portable, but there is no choice as to where they can be plugged in. We shall call this equipment panels 43 to 47.
Now what are these panels, and what do they do? Each panel is an assembly of some equipment. The names of the panels are shown in the accompanying table. The arrangement of Eniac at the Ballistic Research Laboratories as shown in the table is slightly different from the arrangement of Eniac at Moore School.
NAMES OF PANELS OF ENIAC
| Panel No. |
Name (and additional names in some cases) |
|---|---|
| 1 | Initiating Unit |
| 2 | Cycling Unit |
| 3, 4 | Master Programmer, panels 1, 2 |
| 5 | Accumulator 1 |
| 6 | Accumulator 2 |
| 7 | Accumulator 3 |
| 8 | Accumulator 4 (Quotient) |
| 9 | Divider-Square-Rooter |
| 10 | Accumulator 5 (Numerator I) |
| 11 | Accumulator 6 (Numerator II) |
| 12 | Accumulator 7 (Denominator—Square Root I) |
| 13 | Accumulator 8 (Denominator—Square Root II) |
| 14 | Accumulator 9 (Shift I) |
| 15 | Accumulator 10 (Shift II) |
| 16 | Blank panel for new unit (Converter) |
| 17 | Accumulator 11 (Multiplier) |
| 18 | Accumulator 12 (Multiplicand) |
| 19-21 | Multiplier, panels 1, 2, 3 |
| 22[Pg 116] | Accumulator 13 (Left-Hand Partial Products I) |
| 23 | Accumulator 14 (Left-Hand Partial Products II) |
| 24 | Accumulator 15 (Right-Hand Products I) |
| 25 | Accumulator 16 (Right-Hand Products II) |
| 26 | Blank panel for new unit (100 Registers) |
| 27 | Accumulator 17 |
| 28 | Accumulator 18 |
| 29 | Accumulator 19 |
| 30 | Accumulator 20 |
| 31, 32 | Function Table 1, panels 1, 2 |
| 33, 34 | Function Table 2, panels 1, 2 |
| 35, 36 | Function Table 3, panels 1, 2 |
| 37-39 | Constant Transmitter, panels 1, 2, 3 |
| 40-42 | Printer, panels 1, 2, 3 |
| 43-45 | Portable Function Tables A, B, and C |
| 46 | IBM Card Reader |
| 47 | IBM Summary Punch |
Note: The accumulators from which a number can be sent to the printer are now accumulators 1, 2, and 15 to 20.
In reading over the table, we find a number of words that need explaining. Some of the explanation we can give in the summary of the units of Eniac:
SUMMARY OF UNITS OF ENIAC
| Quantity | Device | Significance |
|---|---|---|
| 20 | Accumulators | Store, add, and subtract numbers |
| 1 | Multiplier | Multiplies |
| 1 | Divider-Square-Rooter | Divides, and obtains twice the square root |
| of a number (see Supplement 2) | ||
| 3 | Function Tables | Part of the memory, for referring to |
| tables of numbers | ||
| 1 | Constant Transmitter | Stores numbers from the card reader and |
| from hand-set switches | ||
| 1 | Printer | Punches machine results into cards |
| 1 | Cycling Unit | Controls the timing of the various parts |
| of the machine | ||
| 1 | Initiating Unit | Has controls for starting a calculation, |
| for clearing, etc. | ||
| 1 | Master Programmer | Holds the chief controls for coordinating |
| the various parts of the machine |
An accumulator is a storage counter. It can hold a number; it can clear a number; it can transmit a number either positively or [Pg 117] negatively; and it can receive a number by adding the number in and thus holding the sum of what it held before and the number received. Eniac when first built had only 20 accumulators, and so it could remember only 20 numbers at one time (except for constant numbers set in switches). This small memory was the most serious drawback of Eniac; panel 26 was designed, therefore, to provide a great additional memory capacity.
The divider-square-rooter, as its name tells, is a mechanism that can divide and that can find twice the square root of a number. Eniac is one of the several giant brains that have had square root capacity built into them, particularly since square root is needed for solving trajectories.
Many panels of Eniac have double duty and some have triple duty. For example, panel 24 is an accumulator, but it also (1) stores the right-hand partial products (see Supplement 2) of the multiplier and (2) was a register, when Eniac was at Moore School, from which information to be punched in the printer could be obtained. Clearly, if we have a multiplication to do, we cannot also use this accumulator for storing a number that is to remain unchanged during the multiplication.
The total number of parts in Eniac is near half a million, even if we count electronic tubes as single parts. There are over 18,800 electronic tubes in the machine. It is interesting to note that only 10 kinds of electronic tubes are used in the calculating circuits and only about 60 kinds of resistors and 30 kinds of capacitors. A resistor is a device that opposes the steady flow of electric current through it to a certain extent (called resistance and measured in ohms). A capacitor is a device that can store electrical energy up to a certain extent (called capacitance and measured in farads). All these tubes and parts are standard parts in radios. All types are identified by the color labels established in standard radio manufacturing. It is the combinations of these parts, like the combinations of pieces in a chess game, that give rise to the marvelous powers of Eniac.
The combinations of parts at the first level are called plug-in units. A plug-in unit is a standard box or tray or chassis made of [Pg 118] sheet steel containing a standard assembly of tubes, wires, and other parts. It can be pushed in or pulled out of a standard socket with many connections. An example of a plug-in unit is a decade, or, more exactly, an accumulator decade. This is just a counter wheel or decimal position expressed in Eniac language: it can express successively all the digits from 0 to 9 and then pass from 9 to 0, giving rise to a carry impulse. It is striking that a mechanical counter to hold 10 digits can be made up of 10 little wheels, ¼ inch wide and an inch high. But an accumulator in Eniac, to hold 10 digits, is a set of 10 decades each 2 inches wide and 2½ feet high.
There are only about 20 kinds of plug-in units altogether. Each plug-in unit is interchangeable with any other of the same kind. So, if a decade, for example, shows trouble, you can pull it out of its socket and plug in a spare decade instead.
Numbers in Eniac are of 10 decimal digits with a sign that may be plus or minus. The decimal point is fixed. However, when you are connecting one accumulator with another, you can shift the decimal point if you want to. Also, 2 accumulators may be coupled together so as to handle numbers of 20 digits.
There are three ways by which information—numbers or instructions—can go into the Eniac. Numbers can be put into the machine by means of punch cards fed into the Card Reader, panel 46, or switches on the Constant Transmitter, panels 37 to 39. Numbers or instructions can also go into the machine by means of the Function Tables, panels 43 to 45. Here there are dial switches, which are set by hand. Instructions can also go into the machine by setting the switches, plugging the inputs and outputs, etc., of the wires or lines along which numbers and instructions travel.
There are two ways by which numerical information can come out of the [Pg 119] machine. Numbers can come out of the machine punched on cards by the Summary Punch, panel 47. They are then printed in another room by means of a separate IBM tabulator. Also, numbers can be read out of the machine by means of the lights in the neon bulbs mounted on each accumulator. You can read in the lights of a panel the number held by the accumulator, if the panel is not computing.
Eniac handles information rather differently from any other of the big brains. Instead of having only one bus or “railroad line” along which numbers can be sent, Eniac has more than 10 such lines. They are called digit trays and labeled A, B, C, ···. Each contains 11 digit trunk lines or digit trunks—10 to carry the digits of a number, and the 11th to carry the sign. Instead of having only one telegraph line along which instructions can be sent, Eniac has more than 100 such lines. They are called program trunk lines or program trunks and labeled A1, A2, ···, A11, B1, B2, ···, B11, ···, etc. They are assembled in groups of 11 to a tray; the program trays, in fact, look just like the digit trays, except for their connectors and their purpose, which are different. Below, we shall make clear how the program trays carry control information.
Now, actually, Eniac has many more trunk lines than we have just stated, for each of the lines we have mentioned can be divided into numerous separate sections by the removal of plug connections. How we choose to do this depends on the needs of the problem, the space between the panels, the time when the line is used, etc.
Basically, a number is represented in Eniac by an arrangement of on and off electronic tube elements in pairs, called flip-flops. There is one flip-flop enclosed in a single tube (type 6SN7) for each value 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 for each of the 10 digits stored in an accumulator. So we have at least 100 flip-flops for each accumulator, and thus at least 100 electronic tubes are required to store 10 digits. Actually, an accumulator needs 550 electronic tubes. So we see that [Pg 120] there is not very much of a future in this type of arrangement. The newer electronic brains use different devices for storage of numbers.
In order to show what number is stored in an accumulator, there are 100 little neon bulbs mounted on the face of each accumulator panel. Each bulb glows when the flip-flop that belongs to it is on. For example, suppose that the 4th decade in Accumulator 11 holds the digit 7. Then the 7th flip-flop in that decade will be on, and all the others will be off. The 7th neon bulb for that decade will glow.
Now suppose that the number 7 is in the 4th decade in Accumulator 11 and is to be added into, say, the 4th decade in Accumulator 13. And suppose that it is to be subtracted from the 4th decade in Accumulator 16. What do we do, and what will Eniac do?
First, we pick out 2 digit trays, say B and D. Accumulator 11 has 2 outputs, called the add output and the subtract output. We plug B into the add output and D into the subtract output. Then we go over to Accumulators 13 and 16. They have 5 inputs, that is, 5 ways of being plugged to receive numbers from digit trunks. These inputs are named with Greek letters, α, β, γ, δ, ε. We choose one input, say γ, for Accumulator 13, and we plug B into that input. We choose one input, say ε, for Accumulator 16, and we plug D into that input.
Now we have the “railroad” switching for numbers accomplished. We have set up a channel whereby the number in Accumulator 11 will be routed positively into Accumulator 13 and negatively into Accumulator 16. Now let us suppose that, at some definite time fixed by the control, Accumulator 11 is stimulated to transmit and Accumulators 13 and 16 are conditioned to receive. When this happens, a group of 10 pulses comes along a direct trunk from the cycling unit, and a group of 9 pulses comes along another trunk. We can think of each pulse as a little surge of electricity lasting about 2 millionths of a second. The ten-pulses, as the first group is called, are 10 millionths of a second apart. The nine-pulses, as the second group is called, are also 10 millionths of a second apart but are sandwiched between the ten-pulses. When the 1st ten-pulse comes along, the 7th flip-flop in Accumulator 11 goes off, the 8th flip-flop goes on, the following [Pg 121] nine-pulse goes through and goes out on the subtract line to Accumulator 16. Then the 2nd ten-pulse comes along, the 8th flip-flop goes off, the 9th flip-flop goes on, and the next nine-pulse goes out on the subtract line to Accumulator 16. Now the decade sits at 9, and for this reason the next ten-pulse changes an electronic switch (actually another flip-flop) so that all later nine-pulses will go out on the add line. This ten-pulse also turns off the 9th flip-flop and turns on the 0th flip-flop without causing any carry. Now the 4th of the ten-pulses comes along, turns the 0th flip-flop off, and turns the 1st flip-flop on, and the next nine-pulse goes out on the add line to Accumulator 13. The next 6 of the ten-pulses then come along and change Accumulator 11 back to the digit 7 as before, and the next 6 of the nine-pulses go out to Accumulator 13. Thus Eniac has added 7 into Accumulator 13, has added 2, the nines complement of 7 (see Supplement 2), into Accumulator 16, and has left Accumulator 11 holding the same number as before. This is just the result that we wanted.
In this way, the nines complement of any digit in a decade is transferred out along the subtract line, and the digit unchanged is transmitted out along the add line. As the pulses arrive at any other accumulator, they add into that accumulator.
Eniac performs multiplication by a built-in table of the products in the 10-by-10 multiplication table, using the method of left-hand components and right-hand components (see Supplement 2). For example, suppose that the 3rd digit of the multiplier is 7 and that the 5th digit of the multiplicand is 6. Then, when Eniac attends to the 3rd digit of the multiplier, the right-hand digit of the 42 = 6 × 7 is gathered in one accumulator, and the left-hand digit 4 is gathered in another accumulator. After Eniac has attended to all the digits of the multiplier, then Eniac performs one more addition and transfers the sum of the left-hand digits into the right-hand digits accumulator.
Eniac does division in rather a novel way. First, the divisor is subtracted over and over until the result becomes negative or 0. Then the machine shifts to the next column and adds the divisor until the [Pg 122] result becomes positive or 0. It continues this process, alternating from column to column. For example, suppose that we divide 3 into 84 in this way. We have:
After we subtract 3 the third time, the result becomes negative,-6; in the next column, after we add 3 twice, the result becomes 0. The quotient is
and 3 × 28 is 84. Thus the process checks.
Eniac has three Function Tables. Here you can store numbers or instructions for the machine to refer to. Each Function Table has 104 arguments (see Supplement 2). For each argument, you can store 12 digits and 2 signs that may be plus or minus. This capacity can be devoted to one 12-digit number with a sign, or to two 6-digit numbers each with a sign, or to six 2-digit instructions. The three Function Tables are panels 43, 44, and 45. To put in the numbers or instructions, you have to go over to these panels and set the numbers or instructions, digit by digit, turning dial switches by hand. It is slow and hard to do this right, but once it is done, Eniac can refer to any number or instruction in any table in ¹/₁₀₀₀ of a second. This is much faster than the table reference time in any other of the giant brains built up to 1948.
We said above that Eniac has over 100 control lines or program trunks along which instructions can be sent. These instructions are expressed as pulses called program pulses. Now how do we make these pulses [Pg 123] do what we want them to do? For example, how can we instruct Accumulator 11 to add what it holds into Accumulator 13?
On each unit of Eniac there are plug hubs or sockets (called program-pulse input terminals) to which a program trunk may be connected. A program pulse received here can make the unit act in some desired way. On each accumulator of Eniac, we find 12 program-pulse input hubs. Corresponding to each of these hubs, there is a nine-way switch, called a program-control switch. The setting of this switch determines what the accumulator will do when the program-pulse input hub belonging to the switch receives a program pulse. For instance, there are switch settings for: receive input on the α line, receive input on the β line, etc.; and transmit output on the add line, etc. There is even a switch setting that instructs the accumulator to do nothing, and this instruction may be both useful and important.
Now, in order that Accumulator 11 may transfer a number to Accumulator 13, we need: (1) a digit tray, say B, for the number to travel along; (2) a program trunk line, say G3, to tell Accumulator 11 when to send the number and Accumulator 13 when to receive it; and (3) certain plugging as follows:
1. We plug from program trunk G3 into a program-pulse input hub, say No. 5, of Accumulator 11;
2. We plug from the same program trunk G3 into a program-pulse input hub, say No. 7, of Accumulator 13;
3. We set program-control switch No. 5 of Accumulator 11 to “add”;
4. We set program-control switch No. 7 of Accumulator 13 to some input, say γ.
5. We plug from digit tray B into the add output of Accumulator 11.
6. We plug from digit tray B into the γ input of Accumulator 13.
Now, when the program pulse comes along line G3, it makes Accumulator 13 transmit additively along digit tray B into Accumulator 13. And that is the result that we wanted.
As each mechanism of Eniac finishes what it is instructed to do, it may [Pg 124] or may not put out a program pulse. This pulse in turn may be plugged into any other program trunk line and may stimulate another mechanism to act. Then, when this mechanism finishes, it too may or may not put out a program pulse, and so on.
In general, there are two different ways to instruct Eniac to do a problem. One way is to set all the switches, plug all the connections, etc., for the specific problem. This is a long and hard task. Very often, even with great care, it is done not quite correctly, and then the settings must be carefully checked all over again. A second method (called the von Neumann programming method) is to store all the instructions for a problem in one or two function tables of Eniac and then tell Eniac to read the function tables in sequence and to do what they say. The rest of the machine is then wired up in a standard fashion. This method of instructing Eniac was proposed by Dr. John von Neumann of the Institute of Advanced Study at Princeton, N. J. Eniac has been modified to the slight extent needed so that this method can be used when desired. In this method, each instruction is a selected one of 60 different standard instructions or orders—one of them, for example, being “multiplication.” Each standard order is expressed by 2 decimal digits. The 60 standard orders are sufficient so that Eniac can do any mathematical problem that does not overstrain its capacity. Since each of the 3 Function Tables can hold 600 2-digit instructions, the machine can hold a program of 1800 instructions under the von Neumann programming method.
As a general-purpose calculating machine, Eniac suffers from unbalance. That is to say, Eniac operates rapidly and successfully in some respects, and slowly and troublesomely in other respects. This is altogether to be expected, however, in a calculator as novel as Eniac and made to so large an extent out of standard radio parts. It was certainly better to finish a calculator like this one and then start on a new one, as the Moore School of Electrical Engineering did, than to prolong design and construction indefinitely in order to make improvements. [Pg 125]
Eniac adds or subtracts very swiftly at the rate of 5000 a second. Eniac multiplies at the rate of 360 to 500 a second. Division, however, is slow, relatively; the rate is about 50 a second. Reading numbers from punched cards, 12 a second for 10-digit numbers, is even slower. As a result of these rates, you find, when you put a problem on Eniac, that one division delays you as long as 100 additions or 8 multiplications. Division might have been speeded somewhat by (1) rapidly convergent approximation (see Supplement 2) to the reciprocal of the divisor and (2) multiplying by the dividend; this might have taken 5 or 6 multiplication times instead of 8. Also, the use of a standard IBM punch-card feed and card punch slows the machine greatly. One way to overcome this drawback might be to install one or two additional sets of such equipment, which might increase input and output speed.
Eniac has a very rapid and flexible automatic control over the programming of operations. Eniac has more than 10 channels along which numbers can be transferred and more than 100 channels along which program-control pulses can be transferred. There are many ways for providing subroutines. Eniac has the additional advantage that there is no delay in giving the machine successive instructions: all the instructions the machine may need at any time are ready at the start of the problem, and indications occurring in the calculation can change the routine completely.
All these advantages, however, are paid for rather heavily by the slow methods for changing programming. You have to plug large numbers of program trunk lines and digit trunk lines, or you have to set large numbers of switches, or both. Also, when you wish to return to a previous problem, you must do all the plugging and switch setting over again. Many delays in the operation of the machine are due to human errors in setting the machine for a new problem. Here again, we must remember that Eniac was originally designed as a special-purpose machine for solving trajectories. To calculate a large family of trajectories very little changing of wires and switches would be needed. [Pg 126]
The most severe limitation on the usefulness of Eniac was, at the outset, the fact that it had only 20 registers for storing numbers. There are large numbers of problems that cannot be simply handled with so small an internal memory. Even the Harvard IBM calculator (see Chapter 6) is often strained during a problem because of the number of intermediate results that must be stored for a time before combining. The Ballistic Research Laboratories, however, contracted for extensions to Eniac to provide more memory and easier changing of instructions.
Checking results with Eniac is not easy. There is no built-in guarantee that Eniac’s results are correct. A large calculator can and does make both constant and intermittent errors. Ways for checking with Eniac are:
Mathematical, if and when available, and this will be seldom.
Running the problem a second time, and this will, at most, prove consistency.
Deliberate testing of small parts of the problem, which is very useful and is standard practice but leads only to a probability that the final result is correct.
You can operate Eniac one addition at a time, and even one pulse at a time, and see what the machine shows in its little neon bulbs. This is a very useful partial check.
The cost of Eniac is higher than that of some of the other large mechanical brains—over half a million dollars. Because some of the work was done at the Moore School by students, the cost was probably less than it otherwise would have been. The largest part of the cost was the designing of the machine and the construction of the panels; the tubes were only a small portion of the cost. The tubes used in the calculating circuits cost only 20 to 90 cents. However, no later electronic calculator need cost as much, for many improvements can now be seen. [Pg 127]
The power required for Eniac is about 150 kilowatts or about 200 horsepower, most of which is used for the heaters of the electronic tubes. The largest number of electronic tubes mentioned for future electronic calculators is about 3000, so we can see that they are likely to use less than a quarter of the power needed for Eniac.
Eniac will doubtless give a number of years of successful operation and be extremely useful for problems that employ its assets and are not excluded by its limitations. In fact, at the Ballistic Research Laboratories, for a typical week of actual work, Eniac has already proved to be equal to 500 human computers working 40 hours with desk calculating machines, and it appears that soon two or three times as much work may be obtained from Eniac.
[Pg 128]
In 1946, Bell Telephone Laboratories in New York finished two general-purpose relay calculators—mechanical brains. They were twins. One was shipped in July 1946 to the National Advisory Committee for Aeronautics at Langley Field, Virginia. The other, after some months of trial operation, was shipped in February 1947 to the Ballistic Research Laboratories at the U. S. Army’s Proving Ground, Aberdeen, Md.
Each machine is remarkably reliable and versatile. It can do a wide variety of calculations in a great many different ways. Yet the machine never takes a new step without a check that the old step was correctly performed. There is, therefore, a chance of better than 99.999,999,999 per cent that the machine will not let a wrong result come out. The automatic checking, of course, does not prevent (1) human mistakes—for example, instructing the machine incorrectly—or (2) mechanical failures, in which the machine stops dead in its tracks, letting no result at all come out.
In Bell Telephone Laboratories the telephone system of the country is continually studied. Their research produced the common type of dial telephone system: a masterly machine for selecting information.
Now when a telephone engineer studies an electric circuit, he often [Pg 129] finds it very convenient to use numbers in pairs: like 2, 5 or-4,-1. Here the comma is a separation sign to keep the two numbers in the pair separate and in sequence. Mathematicians call numbers of this kind, for no very good reason, complex numbers; of course, they are far less complex than why the sun shines or why plants grow.
When Bell Laboratories test the design of new circuits, girl computers do arithmetic with complex numbers. Addition and subtraction are easy: each means two operations of addition or subtraction of ordinary numbers. For example, 2, 5, plus-4,-1 equals 2-4, 5-1, which equals-2, 4. And 2, 5 minus-4,-1 is the same as 2, 5 plus 4, 1; and this equals 2 + 4, 5 + 1, which equals 6, 6. Multiplication of two complex numbers, however, is more work. If a, b and c, d are two complex numbers, then the formula for their product is (a × c)-(b × d), (a × d) + (b × c). To get the answer, we need 4 multiplications, 1 subtraction, and 1 addition. Division of two complex numbers requires even more work. If a, b and c, d are two complex numbers, the formula for the quotient of a, b divided by c, d is:
[(a × c) + (b × d)] ÷ [(c × c) + (d × d)],
[(b × c) - (a × d)] ÷ [(c × c) + (d × d)]
For example,
(2, 5) ÷ (-4, -1) = [(2 × -4 = -8) + (5 × -1 = -5)] ÷ [(-4 × -4 = 16) + (-1 × -1 = 1)],
[(5 × -4 = -20) - (2 × -1 = -2)] ÷ [16 + 1] = -(¹³/₁₇), -(¹⁸/₁₇)
Thus, division of one complex number by another needs 6 multiplications, 2 additions, 1 subtraction, and 2 divisions of ordinary numbers—and always in the same pattern or sequence.
About 1939, an engineer at Bell Telephone Laboratories in New York, Dr. George R. Stibitz, noticed the great volume of this pattern arithmetic. He began to wonder why telephone switching equipment could not be used to do the multiplications and divisions automatically. He decided it could. All that was necessary was that the relays (see Chapter 2) [Pg 130] used in regular telephone equipment should have a way of remembering and calculating with numbers. Regular telephone equipment would take care of the proper sequence of operations. Regular equipment known as teletypewriters would print the numbers of the answer when it was obtained. A teletypewriter consists essentially of a typewriter that may be operated by electrical impulses. It has a keyboard that may produce electrical impulses in sets corresponding to letters; and it can receive or transmit over wires.
Dr. Stibitz coded the numbers: each decimal digit was matched up with a group of four relays in sequence, and each of these relays could be open or closed. If 0 means open and 1 means closed, here is the pattern or code that he used:
| Decimal Digit |
Relay Code |
|---|---|
| 0 | 0011 |
| 1 | 0100 |
| 2 | 0101 |
| 3 | 0110 |
| 4 | 0111 |
| 5 | 1000 |
| 6 | 1001 |
| 7 | 1010 |
| 8 | 1011 |
| 9 | 1100 |
With regular telephone relays and regular telephone company techniques, Dr. Stibitz and Bell Telephone Laboratories designed and constructed the machine. It was called the Complex Computer and was built just for multiplying and dividing complex numbers. Six or eight panels of relays and wires were in one room. Two floors away, some of the girl computers sat in another room, where one of the teletypewriters of the machine was located. When they wished, they could type into the machine’s teletypewriter the numbers to be multiplied or divided. In a few seconds back would come the answer. In fact, there were two more computing rooms where teletypewriters of the machine were stationed. To prevent conflicts between stations, the machine had a circuit like the busy signal from a telephone.
In 1940, a demonstration of the Complex Computer took place: the [Pg 131] computing panels remained in New York, but the teletypewriter input-output station was set up at Dartmouth College in Hanover, N. H. Mathematicians gave problems to the machine in Dartmouth, it solved them in New York, and it reported the answers in Dartmouth.
With this as a beginning, Bell Laboratories developed another machine for a wide variety of mathematical processes called interpolating (see Supplement 2). Then, during World War II, Bell Laboratories made more special-purpose computing machines. They were used in military laboratories charged with testing the accuracy of instruments for controlling the fire of guns. These computers took in a set of gun-aiming directions put out by the fire-control instrument in some test. They also took in the set of observations that went into the fire-control instrument on that test. Then they computed the differences between the gun-aiming produced by the fire-control instrument and the gun-aiming really required by the observations. Using these differences, the fire-control instrument could be adjusted and corrected. These special-purpose computers were also useful in checking the design of new fire-control instruments and in checking changes due to new types of guns or explosives.
Regularly, after each of these special-purpose computers was finished, people began to put other problems on it. It seemed to be fated that, as soon as you had made a machine for one purpose, you wanted to use it for something else. Accordingly, in 1944, two agencies of the U. S. Government together made a contract with Bell Telephone Laboratories for two general-purpose relay computers. These two machines were finished in 1946 and are twins.
When a man sits down at a desk to work on a computation, he has six things on his desk to work with: a work sheet; a desk calculator, to add, subtract, multiply, and divide; some rules to be followed; the tables of numbers he will need; the data for the problem; and an answer sheet. In his head, he has the capacity to make decisions and to do his [Pg 132] work in a certain sequence of steps. These seven subdivisions of calculation are all found in the Bell Laboratories’ general-purpose relay computer. The general-purpose computer is a computing system, in fact, more than it is a single machine. The part of the system which does the actual calculating is called, in the following paragraphs, the computer, or else, since it is in two halves, Computer 1 and Computer 2.
The computing system delivered to the Ballistic Research Laboratories fills a room about 30 by 40 feet and consists of the following:
2 computers: panels of relays, wiring, etc., which add, subtract, multiply, divide, select, decide, control, etc.
4 problem positions: tables each holding 12 mechanisms for feeding paper tape, which read numbers and instructions punched on tape and convert them into electrical impulses.
2 hand perforators: keyboard devices for punching instructions and numbers on paper tape.
1 processor: a table holding mechanisms for feeding 2 paper tapes and punching a third paper tape, used for checking numbers and instructions punched on tape.
2 recorders: each a table holding a teletypewriter, a tape punch, and a tape feed, used for recording answers and, if necessary, consulting them again.
The 2 computers correspond to the work sheet, the desk calculator, and the man’s capacity to make decisions and to carry out a sequence of steps. The 4 problem positions correspond to the problem data, the rules, and the tables of numbers. The 2 recorders correspond to the answer sheet. The 2 hand perforators and the processor are auxiliary machines: they translate the ordinary language of arithmetic into the machine language of punched holes in paper tape.
This is the computing system as organized for the Ballistic Research Laboratories at Aberdeen. The one for the National Advisory Committee for Aeronautics has only 3 problem positions. The computer system may, in fact, be organized with 1 to 10 computers and with 1 to 20 problem positions. [Pg 133]
The great bulk of this computing system, like the mechanical brains described in previous chapters, is made up of large numbers of identical parts of only a few kinds. These are: standard telephone relays; wire; and standard teletype transmitters, mechanisms that read punched paper tape and produce electrical impulses.
The numbers that the Bell machine contains range from 0.1000000 to 0.9999999 times a power of 10 varying from 10,000,000,000,000,000,000 to 0.000,000,000,000,000,000,1, or, in other words, from 10¹⁹ to 10⁻¹⁹. The machine also contains zero and infinity: zero arises when the number is smaller than 10⁻¹⁹, and infinity arises when the number is equal to or greater than 9,999,999,000,000,000,000. (See Supplement 2.)
The system used in the machine to represent numbers on relays is called biquinary—the bi-, because it is partly twofold like the hands, and the -quinary because it is partly fivefold like the fingers. This system is used in the abacus (see Chapter 2 and Supplement 2). In the machine, for each decimal digit, 7 relays are used. These relays are called the 00 and 5 relays, and the 0, 1, 2, 3, and 4 relays. If, as before, 0 indicates a relay that is not energized and 1 indicates a relay that is energized, then each decimal digit is represented by the positioning of the 7 relays as follows:
| Decimal Digit |
Relays | ||
|---|---|---|---|
| 00 | 5 | 0 1 2 3 4 | |
| 0 | 1 | 0 | 1 0 0 0 0 |
| 1 | 1 | 0 | 0 1 0 0 0 |
| 2 | 1 | 0 | 0 0 1 0 0 |
| 3 | 1 | 0 | 0 0 0 1 0 |
| 4 | 1 | 0 | 0 0 0 0 1 |
| 5 | 0 | 1 | 1 0 0 0 0 |
| 6 | 0 | 1 | 0 1 0 0 0 |
| 7 | 0 | 1 | 0 0 1 0 0 |
| 8 | 0 | 1 | 0 0 0 1 0 |
| 9 | 0 | 1 | 0 0 0 0 1 |
Then, for any decimal digit, one and only one of [Pg 134] the 00 and 5 relays is energized, and one and only one of the 0, 1, 2, 3, and 4 relays is energized. If more or less than exactly one relay in each set is energized, then the machine knows that it has made a mistake, and it stops dead in its tracks. Thus any accidental failure of a relay is at once caught, and the chance of two compensating failures occurring at the same time is extremely small.
In order to put a problem into this machine—just as with the other machines—first a mathematician who knows how the problem is to be solved, and who knows how to organize it for the machine, lays out the scheme of calculation. Then, a girl goes to one of the hand perforators. Sitting at the keyboard, she presses keys and punches out feet or yards of paper tape expressing the instructions and numbers for the calculation. Each character punched—digit, letter, or sign—has one or more of a maximum of 6 holes across the tape. Another girl, using the other hand perforator, also punches out the instructions and numbers for the calculation. If she wishes to erase a wrong character, she can press an erase key that punches all 6 holes, and then the machine will pass by this row as if it were not there.
Three kinds of tapes are produced for the machine:
Problem tapes, which contain information belonging to the particular problem.
Table tapes, which contain tables of numbers to be referred to from time to time.
Routine tapes, which contain the program, or routine, or sequence of steps that the machine is to carry out.
In each of these tapes one character takes up ⅒ of an inch along the tape. In the case of a table tape, however, an ordinary 1-digit number requires 4 characters on the tape, and a 7-digit number requires 11 characters on the tape. On a table tape there will be on the average about 1 inch of tape per number.
The two paper tapes prepared on the perforator should agree. But [Pg 135] whether or not they agree, a girl takes them over to the processor and puts them both in. The processor has two tape feeds, and she puts one tape on each and starts the machine. The processor compares them row by row, making sure that they agree, and punches a new tape row by row. If the two input tapes disagree, the processor stops. You can look to see which tape is right, and then you can put the correct punch into the new tape with a keyboard mounted on the processor. As the processor compares the two input tapes, it also converts any number written in the usual way into machine language. For example, the processor will automatically translate 23,188 into +.231 8800 × 10⁺⁵. The processor also puts in certain safeguards. If you want it to, the processor will also make a printed record of a tape. Also, when a tape becomes worn from use in the machine, you can put it into the processor and make a fresh copy.
Next, the girl takes the punched tape made by the processor over to a problem position that is idle. Two of the problem positions are always busy guiding the two computers. The other two problem positions stand by, ready to be loaded with problems.
A problem position looks like a large covered-over table. Under the covers are 12 tape feeds, or tape transmitters. All these transmitters look exactly alike except for their labels and consist of regular teletype transmitters. Six-hole paper tape can be fed into any transmitter. Six metal fingers sense the holes in the paper tape and give out electrical impulses at proper times. At the front of the problem position is a small group of switches that provide complete control over the problem while it is on the machine. These are switches for starting, disconnecting, momentary stop, etc.
One tape transmitter is the problem tape transmitter. It takes in all the data for the problem such as the starting numbers. The first thing it does at the start of a problem is to check (by comparing tape numbers) that the right tapes are in the right feeds.
Five transmitters are routine tape transmitters. Each of these takes in [Pg 136] the sequence of computing steps. The routine tapes also contain information for referring to table tapes and instructions for printing and punching tape. The machine can choose according to instructions between the five routine tapes and can choose between many different sections on each tape. Therefore, we can use a large number of different routines in a calculation, and this capacity makes the machine versatile and powerful.
Six transmitters are table tape transmitters. They read tables of numbers when directed to. A table tape can be as long as 100 feet and will hold numbers at the rate of 1 inch per number, so that about 1200 numbers of seven decimal digits can be stored on a table tape.
When we look up a number in a table, such as the following,
| 2½ | 3 | 3½ | ··· | |
| 1 | 1.02500 | 1.03000 | 1.03500 | |
| 2 | 1.05063 | 1.06090 | 1.07123 | |
| 3 | 1.07689 | 1.09273 | ··· | |
| 4 | 1.10381 | ··· | ··· | |
| 5 | 1.13141 | ··· | ||
| 6 | 1.15969 | |||
| 7 | ··· | |||
| 8 | ··· | |||
| 9 | ··· | |||
| 10 | ||||
| ··· | ··· | |||
we look along the top and down the side until we find the column and row of the number we are looking for. These are called the arguments of the tabular value that we are looking for (see Supplement 2). Now when we put this table on a tape to go into the Bell Laboratories machine, we write it all on one line, one figure after another, and we punch it as follows:
2-½ 1-5 1.02500 1.05063 1.07689 1.10381 1.13141
6-10 1.15969 ··· 11-15 ··· ··· ··· 3 1-5
1.03000 1.06090 ··· ··· 3½ 1-5 1.03500 ···
You will notice that the column labels 2½, 3, 3½ have been put on the tape, each in front of the group of numbers they apply to. The row labels 1 to 5, 6 to 10, ··· have also been put on the tape, each in front of the group of numbers they apply to. The [Pg 137] appropriate column and row numbers, or arguments, must be put often on every table tape, so that it is easy for the machine to tell what part of the table tape it is reading.
In the Bell Laboratories machine, we do not need to put equal blocks of arguments like 1-5, 6-10 ··· on the table tape. Instead we can put individual arguments like 1, 2, 3, 4 ···, or, if we wish, we can use blocks of different sizes, like 1-3, 4-15, 16-30···. For some tables, such as income tax tables, it is very useful to have varying-sized blocks of arguments. The machine, when hunting for a certain value in the table, makes a comparison at each block of arguments.
The machine needs about 6 seconds to search a foot of tape. If we want to set up a table economically, therefore, we need to consider the average length of time needed for searching.
Fig. 1. Scheme of a recorder.
At either one of the two recorders (Fig. 1), information comes out of the machine, either in the form of printed characters or as punched tape. The recorder consists of a printer, a reperforator, and a tape transmitter. One recorder table belongs to each computer and records the results it computes. The printer is a regular teletypewriter connected to the machine. It translates information produced by the machine as electrical impulses and prints the information in letters and digits on paper. The reperforator is an [Pg 138] automatic tape punch. It translates information produced by the machine in the form of electrical impulses and punches the information on paper tape. Next to the tape punch is a tape transmitter. After the tape comes through the punch, it is fed into the transmitter. Here the machine can hunt for a previous result punched in the tape, read that result, and use it again.
The main part of the computing system consists of 27 large frames loaded with relays and wiring, called the computer, or Computer 1 and Computer 2. In this “telephone central station,” all the “phone calls” from one number to another are attended to. There are 8 types of these frames in the computer:
| Frames | Number |
|---|---|
| Storing register frames | 6 |
| Printer frames | 2 |
| Problem frames | 2 |
| Position frames | 2 |
| Calculator frames | 6 |
| Control frames | 2 |
| Routine frames | 4 |
| BTL (Block-Trig-Log) frames | 2 |
| Permanent table frames | 1 |
| Total | 27 |
In most but not quite all respects, the two halves, Computer 1 and Computer 2, can compute independently. The storing register frames hold enough relays to store 30 numbers. The registers for these numbers are named A, B, C, D, ···, M, N, O in two groups of 15 each. One group belongs to Computer 1 and the other to Computer 2. In each Computer, the calculator frames hold enough relays for storing two numbers (held in the X and Y registers) and for performing addition, subtraction, multiplication, division, and square root. In each Computer, the problem frame stores the numbers that are read off the problem tape and the table tapes, and the printer frame stores the numbers that are read into the printer. The printer frame also stores indications, for example, the signs of numbers, plus or minus, for [Pg 139] purposes of combining them. These frames also hold the relays that control the printer, the problem tape, and the table tapes. Jointly for both Computers, the position frames connect a problem in some problem position to a Computer that becomes idle. For example, one problem may finish in the middle of the night; the machine automatically and unattended switches to another problem position and proceeds with the instructions there contained. A backlog of computing on hand can be stored in two of the problem positions, while the other two control the two Computers. In each Computer, the routine frames hold the relays that make the Computer follow the routine instructions. Jointly for both Computers, the remaining frames—the control frames, the BTL frames, and the permanent table frames—hold the relays that control: the alarms and lights for indicating failures; some circuits called the BTL controls; the tape processor; and the mathematical tables that are permanently wired into the machine. The permanent table frames hold the following mathematical functions (see Supplement 2): sine, cosine, antitangent, logarithm, and antilogarithm.
Numbers can be stored in the machine in the 30 regular storing registers of both Computers together. They can also be stored, at the cost of tying up some machine capacity, in the other registers: the 4 calculator registers, the 2 problem registers, the 2 table registers, and the 2 printer registers. Numbers can also be punched out on tape, in either of the two printers, and later read again from the tape. Labels identifying the numbers can also be punched and read again from the tape.
Each register in the machine stores a number in the biquinary notation, as explained above. In programming the machine, after mentioning a register it is necessary—as a part of the scheme for checking—to tell the machine specifically whether to hold the number in the register or to clear it.
The calculator frames can add two numbers together, if so instructed in the routine tape. Suppose that the two numbers are in the registers [Pg 140] B and D and that we wish to put the sum in register F. Suppose that we wish to clear the D number but hold the B number after using them. The code on the routine tape is B H + D C = F. H and C coming right after the names of the registers always designate “hold” and “clear,” respectively.
The calculator frames can, likewise, subtract a number. The routine instruction B H-D C = F means:
The calculator frames perform multiplication by storing the digits of the multiplier, adding the multiplicand over and over, and shifting, until the product is obtained. However, if the multiplier is 1989, for example, the calculator treats it as 2000-11. This short-cut applies to digits 6, 7, 8, 9 and cuts the time required for multiplying. The routine instruction is B H × D C = F.
The calculator performs division by repeated subtraction. The routine instruction is B H ÷ D C = F. The operation signs +,-, ×, ÷ actually appear on the keyboard of the perforator and on the printed tape produced by the printer.
Discrimination is the term used in the Bell Laboratories computer for what we have previously called selection, or comparison, or sequencing. The discriminator is a part of the calculator that compares or selects or decides—“discriminates.” The discriminator can decide whether a number is zero or not zero. In the language of the algebra of logic (see Chapter 9 and Supplement 2), if a is a number, the discriminator can find T(a = 0). The discriminator can also decide whether a number is positive or negative. In the language of logic, it can find T(a > 0) or T(a < 0). The actions that a discriminator can cause to be taken are:
[Pg 141] In this way the discriminator can:
Among the problems that have been placed on the machine successfully are: solving the differential equation of a trajectory (see Chapter 5) and solving 32 linear simultaneous equations in 32 unknowns (see Supplement 2). In the second case, the routine tapes were designed to apply equally well to 11 to 100 linear equations in 11 to 100 unknowns. However, the machine can do a very broad class of problems, including, for example, computing a personal income tax. This calculation with all its complexity of choices cannot be placed on any of the mechanical brains described in previous chapters. The machine can, of course, be used to calculate any tables that we may wish to refer to.
The Bell Telephone Laboratories general-purpose relay computer is probably the best mechanical brain made up to the end of 1947, in regard to the two important factors of reliability and versatility.
The machine produces results that are practically 100 per cent reliable, for the machine checks each step before taking the next one. The checking principle is that exactly a certain number of relays must be energized. For example, as we said before, for each decimal digit there are 7 relays. Exactly 2 of these relays must be energized—no more, no less. If this does not happen, the machine stops at once without losing any numbers. Lights shine for many circuits in the [Pg 142] control panel, and, if you compare what they ought to show with what they do show, you can usually find at once the location of the mistake. The trouble may be a speck of dirt between two contact points on a relay, and, when it is brushed away, the machine can go right ahead from where it stopped. According to a statement by Franz L. Alt, director of the computing laboratory at the Ballistic Research Laboratories, in December 1947, “the Bell machine had not given a single wrong result in eight months of operation, except when operators interfered with its normal running.”
To guard against the risk of putting tapes in the wrong transmitters, the machine will check by the instructions contained in the tapes that the right tapes are in the right places.
The time required to do problems on this mechanical brain is perhaps longer than on the others. The numbers are handled digit by digit on the input tapes, and the typewriter in the recorder moves space by space in order to get to the proper writing point. These are slow procedures. The speeds of numerical operation are: addition, ³/₁₀ second; multiplication, 1 second on the average; division, 2.7 seconds on the average; square root, 4.5 seconds on the average; logarithm, about 15 seconds.
In order to operate the machine, the staff required is: one maintenance man; one mathematical engineer; about six girls for punching tape, etc., depending on the number of problems to be handled at the rate of about one problem per week per girl. Unlike any of the other mechanical brains built by the end of 1947, this machine will run unattended.
The relays in the machine will operate for years with no failure; they have the experience of standard telephone techniques built into them. Under laboratory conditions this type of relay had by 1946 operated successfully much more than 100 million times. The tape feeding and reading equipment in the machine may be maintained by periodic [Pg 143] inspection and service. The total number of teletype transmitters in the machine is 38. If one fails, it is easy to plug in a spare.
The total power required for the machine is about 28 horsepower. Batteries are furnished so that, if the power supply should be interrupted, the machine can still operate for as long as a half-hour.
The cost of production of this machine in the size of 4 problem positions and 2 computers has been roughly estimated as half a million dollars. This cost includes material, manufacture, installation, and testing. No development cost is included in this figure. Instead, the cost of development has been reckoned as squaring with patents and other contributions of the work to the telephone switching art.
It is unlikely that the general-purpose relay computer will be manufactured generally. The pressure of orders for telephones, the need to catch up with the backlog of demand, and the development of electronic computers—all indicate that the Bell system will hardly go further with this type of computer. In an emergency, however, the Bell system would probably construct such machines for the government, if requested. In the meantime, many principles first used in the general-purpose relay computer are likely to find applications in telephone system work. In fact, a present major development being pursued in the telephone sections of Bell Laboratories is the application of the computer principles to the automatic computation of telephone bills.
[Pg 144]
So far we have talked about mechanical brains that are mathematicians. They are fond of numbers; their main work is with numbers; and the other kinds of thinking they do are secondary. We now come to a mechanical brain that is a logician. It is fond of reasoning—logic; its main work is with what is logically true and what is logically false; and it does not handle numbers. This mechanical brain was finished in June 1947. It is called the Kalin-Burkhart Logical-Truth Calculator. As its name tells, it calculates logical truth. Now what do we mean by that?
To be true or false is a property of a statement. Usually we say that a statement is true when it expresses a fact. For example, take the statement “Salt dissolves in water.” We consider this statement to be true because it expresses a fact. Actually, in this case we can roughly prove the fact ourselves. We take a bowl, put some water in it, and put in a little salt. After a while we look into the water and notice that no salt whatever is to be seen.
Of course, this statement, like many another, occurs in a context where certain things are understood. One of the understandings here, for example, is “a small amount of salt in a much larger amount of water.” For if we put a whole bag full of salt in just a little water, not all the salt will dissolve. Nearly every statement occurs in a context that we must know if we are to decide whether the statement is true or false. [Pg 145]
Logical truth is different from ordinary truth. With logical truth we appeal not to facts but to suppositions. Usually we say that a statement is logically true when it follows logically from certain suppositions. In other words, we play a game that has useful, even wonderful, results. The game starts with “if” or “suppose” or “let us assume.” While the game lasts, any statement is logically true if it follows logically from the suppositions.
For example, let us take five statements:
Let us also take a certain context in which: We know what we mean by such words as “earth,” “flat,” “falling,” etc.; we have other statements and understandings such as “if John Doe walks off the edge of a cliff, he will fall,” “a flat sheet of paper has an edge,” etc. In this context, if statements 1 and 3 are supposed, then statement 4 is logically true. On the other hand, if statements 2 and 3 are supposed, then statement 5 is logically true. Of course, for many centuries, nearly all men believed statement 1; and the importance of the years 1492 to 1521 (Columbus to Magellan) is linked with the final proof that statement 2 expresses a fact. So, depending on the game, or the context, whichever we wish to call it, almost any statement can be logically true. What we become interested in, therefore, is the connections between statements which make them follow logically.
Perhaps the most familiar example of “following logically” is a pattern of words like the following:
[Pg 146] If statements 1 and 2 are supposed, then statement 3 is logically true. In other words, statement 3 logically follows from statements 1 and 2. This word pattern is logically true, no matter what substitutions we make for igs, ows, and umphs. For example, we can replace igs by men, ows by animals, and umphs by mortals, and obtain:
The invented words “igs,” “ows,” “umphs” mark places in the logical pattern where we can insert any names we are interested in. The words “all,” “are,” “therefore” and the ending s mark the logical pattern. Of course, instead of using invented words like “igs,” “ows,” “umphs” we would usually put A’s, B’s, C’s. This logical pattern is called a syllogism and is one of the most familiar. But there are even simpler logical patterns that are also familiar.
Many simple logical patterns are so familiar that we often use them without being conscious of doing so. The simple logical patterns are marked by words like “and,” “or,” “else,” “not,” “if,” “then,” “only.” In the same way, simple arithmetical patterns are marked by words like “plus,” “minus,” “times,” “divided by.”
Let us see what some of these simple logical patterns are. Suppose that we take two statements about which we have no factual information that might interfere with logical supposing:
In practice, we might be concerned with such statements when writing the rules governing a plan of insurance for a group of employees. Here, we shall play a game: [Pg 147]
(1) We shall make up some new statements from statements 1 and 2, using the words “and,” “or,” “else,” “not,” “if,” “then,” “only.”
(2) We shall examine the logical patterns that we can make.
(3) We shall see what we can find out about their logical truth.
Suppose we make up the following statements:
3. John Doe is not eligible for insurance.
4. John Doe does not require a medical examination.
5. John Doe is eligible for insurance and requires a medical examination.
6. John Doe is eligible for insurance, and John Doe is eligible for insurance.
7. John Doe is eligible for insurance, or John Doe requires a medical examination.
8. If John Doe is eligible for insurance, then he requires a medical examination.
9. John Doe requires a medical examination if and only if he is eligible for insurance.
10. John Doe is eligible for insurance or else he requires a medical examination.
Now clearly it is troublesome to repeat quantities of words when we are interested only in the way that “and,” “or,” “else,” “not,” “if,” “then,” “only” occur. So, let us use just 1 and 2 for the two original statements, remembering that “1 and 2” means here “statement 1 AND statement 2” and does not mean 1 plus 2. Then we have:
| 3: | not-1 |
| 4: | not-2 |
| 5: | 1 and 2 |
| 6: | 1 and 1 |
| 7: | 1 or 2 |
| 8: | if 1, then 2 |
| 9: | 1 if and only if 2 |
| 10: | 1 or else 2 |
Here then are some simple logical patterns that we can make.
Now what can we find out about the logical truth of statements 3 to 10? [Pg 148] If we know something about the truth or falsity of statements 1 and 2, what will logically follow about the truth or falsity of statements 3 to 10? In other words, how can we calculate the logical truth of statements 3 to 10, given the truth or falsity of statements 1 and 2?
For example, 3 is not-1; that is, statement 3 is the negative or the denial of statement 1. It follows logically that, if 1 is true, 3 is false; if 1 is false, 3 is true. Suppose that we use T for logically true and F for logically false. Then we can show our calculation of the logical truth of statement 3 in Table 1.
| Table 1 | Table 2 | |||
| 1 | not-1 = 3 | 2 | not-2 = 4 | |
| T | F | T | F | |
| F | T | F | T | |
Our rule for calculation is: For T put F; for F put T. Of course, exactly the same rule applies to statements 2 and 4 (see Table 2). The T and F are called truth values. Any meaningful statement can have truth values. This type of table is called a truth table. For any logical pattern, we can make up a truth table.
Let us take another example, “and.” Statement 5 is the same as statement 1 and statement 2. How can we calculate the logical truth of statement 5? We can make up the same sort of a table as before. On the left-hand side of this table, there will be 4 cases:
On the right-hand side of this table, we shall put down the truth value of statement 5. Statement 5 is true if both statements 1 and 2 are true; statement 5 is false in the other cases. We know this from our common everyday experience with the meaning of “and” between statements. So we can set up the truth table, and our rule for calculation of logical truth, in the case of and, is shown on Table 3. [Pg 149]
Table 3
| 1 | 2 | 1 and 2 = 5 |
| T | T | T |
| F | T | F |
| T | F | F |
| F | F | F |
“and” and the other words and phrases joining together the original two statements to make new statements are called connectives, or logical connectives. The connectives that we have illustrated in statements 7 to 10 are: or, if ··· then, if and only if, or else.
Table 4 shows the truth table that applies to statements 7, 8, 9, and 10. This truth table expresses the calculation of the logical truth or falsity of these statements.
Table 4
| 1 or 2 | if 1, then 2 | 1 if and only if 2 | 1 or else 2 | ||
| 1 | 2 | = 7 | = 8 | = 9 | = 10 |
| T | T | T | T | T | F |
| F | T | T | T | F | T |
| T | F | T | F | F | T |
| F | F | F | T | T | F |
The “or” (as in statement 7) that is defined in the truth table is often called the inclusive “or” and means “and/or.” Statement 7, “1 or 2,” is considered to be the same as “1 or 2 or both.” There is another “or” in common use, often called the exclusive “or,” meaning “or else” (as in statement 10). Statement 10, “1 or else 2,” is the same as “1 or 2 but not both” or “either 1 or 2.” In ordinary English, there is some confusion over these two “or’s.” Usually we rely on the context to tell which one is intended. Of course, such reliance is not safe. Sometimes we rely on a necessary conflict between the two statements connected by “or” which prevents the “both” case from being possible. In Latin the two kinds of “or” were distinguished by different words, vel meaning “and/or,” and aut meaning “or else.” [Pg 150]
The “if ··· then” that is defined in the truth table agrees with our usual understanding that (1) when the “if clause” is true, the “then clause” must be true; and (2) when the “if clause” is false, the “then clause” may be either true or false. The “if and only if” that is defined in the truth table agrees with our usual understanding that (1) if either clause is true, the other is true; and (2) if either clause is false, the other is false.
In statement 6, there are only two possible cases, and the truth table is shown in Table 5.
Table 5
| 1 | 1 and 1 = 6 |
| T | T |
| F | F |
We know that 6 is true if and only if 1 is true. In other words, the statement “1 and 1 if and only if 1” is true, no matter what statement 1 may refer to. It is because of this fact that we never use a statement in the form “1 and 1”: it can always be replaced by the plain statement “1.”
Now you may say that this is all very well, but what good is it? Almost anybody can use these connectives correctly and certainly has had a great deal of practice using them. Why do we need to go into truth values and truth tables?
When we draft a contract or a set of rules, we often have to consider several conditions that give rise to a number of cases. We must avoid:
1. All conflicts, in which two statements that disagree apply to the same case.
2. All loopholes, in which there is a case not covered by any statement.
If we have one statement or condition only, we have to consider 2 possible cases: the condition satisfied or the statement true; [Pg 151] the condition not satisfied or the statement false. If we have 2 conditions, we have to consider 4 possible cases: true, true; false, true; true, false; false, false. If we have 3 conditions, we have to consider 8 possible cases one after the other (see Table 6).
Table 6
| Case | 1st Condition |
2nd Condition |
3rd Condition |
| 1 | T | T | T |
| 2 | F | T | T |
| 3 | T | F | T |
| 4 | F | F | T |
| 5 | T | T | F |
| 6 | F | T | F |
| 7 | T | F | F |
| 8 | F | F | F |
Instead of T’s and F’s, we would ordinarily use check-marks (✓) and crosses (✕), which, of course, have the same meaning. We may consider and study each case individually. In any event, we must make sure that the proposed contract or set of rules covers all the cases without conflicts or loopholes.
The number of possible cases that we have to consider doubles whenever one more condition is added. Clearly, it soon becomes too much work to consider each case individually, and so we must turn to a second method, thoughtful classifying and reasoning about classes of cases.
Now suppose that the number of conditions increases: 4 conditions give rise to 16 possible cases; 5, 6, 7, 8, 9, 10, ··· conditions give rise to 32, 64, 128, 256, 512, 1024, ··· cases respectively. Because of the large number of cases, we soon begin to make mistakes while reasoning about classes of cases. We need a more efficient way of knowing whether all cases are covered properly.
One of the more efficient ways of reasoning is often called the algebra of logic. This algebra is a part of a new science called mathematical logic. Mathematical logic is a science that has the following characteristics: [Pg 152]
Mathematical logic studies especially the logical relations expressed in such words as “or,” “and,” “not,” “else,” “if,” “then,” “only,” “the,” “of,” “is,” “every,” “all,” “none,” “some,” “same,” “different,” etc. The algebra of logic studies especially only the first seven of these words.
The great thinkers of ancient Greece first studied the problems of logical reasoning as these problems turned up in philosophy, psychology, and debate. Aristotle originated what was called formal logic. This was devoted mainly to variations of the logical pattern shown above called the syllogism. In the last 150 years, the fine symbolic techniques developed by mathematicians were applied to the problems of the calculation of logical truth, and the result was mathematical logic, much broader and much more powerful than formal logic. A milestone in the development of mathematical logic was The Laws of Thought, written by George Boole, a great English mathematician, and published in 1854. Boole introduced the branch of mathematical logic called the algebra of logic, also called Boolean algebra. In late years, all the branches of mathematical logic have been improved and made easier to use.
We can give a simple numerical example of Boolean algebra and how it can calculate logical truth. Suppose that we take the truth value of a statement as 1 if it is true and 0 if it is false. Now we have numbers 1 and 0 instead of letters T and F. Since they are numbers, we can add them, subtract them, and multiply them. We can also make up simple numerical formulas that will let us calculate logical truth. If P and Q are statements, and if p and q are their truth values, respectively, we have Table 7.
Table 7
| Statement | Truth Value |
|---|---|
| not-P | 1 - p |
| P and Q | pq |
| P or Q | p + q - pq |
| if P, then Q | 1 - p + pq |
| P if and only if Q | 1 - p - q + 2pq |
| P or else Q | p + q - 2pq |
[Pg 153] For example, suppose that we have two statements P and Q:
To test that the truth value of “P or Q” is p + q-pq, let us put down the four cases, and calculate the result (see Table 8).
Table 8
| p | q | p + q - pq |
| 1 | 1 | 1 + 1 - 1 = 1 |
| 0 | 1 | 0 + 1 - 0 = 1 |
| 1 | 0 | 1 + 0 - 0 = 1 |
| 0 | 0 | 0 + 0 - 0 = 0 |
Now we know that P or Q is true if and only if either one or both of P and Q are true, and thus we see that the calculation is correct.
The algebra of logic (see also Supplement 2) is a more efficient way of calculating logical truth. But it is still a good deal of work to use the algebra. For example, if we have 10 conditions, we shall have 10 letters like p, q to handle in calculations. Thus we need a still more efficient way.
In 1937 a research assistant at Massachusetts Institute of Technology, Claude E. Shannon, was studying for his degree of master of science. He was enrolled in the Department of Electrical Engineering. He was interested in automatic switching circuits and wondered why an algebra should not apply to them. He wrote his thesis on the answer to this question and showed that:
A paper, based on his thesis, was published in 1938 in the Transactions of the American Institute of Electrical Engineers with the title “A Symbolic Analysis of Relay and Switching Circuits.” [Pg 154]
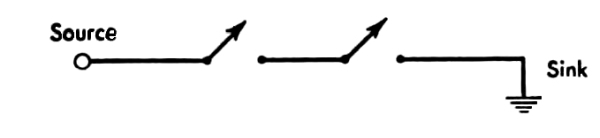
Fig. 1. Switches in series.
For a simple example of what Shannon found out, suppose that we have two switches, 1, 2, in series (see Fig. 1). When do we get current flowing from the source to the sink? There are 4 possible cases and results (see Table 9).
Table 9
| Switch 1 is closed |
Switch 2 is closed |
Current flows |
|---|---|---|
| Yes | Yes | Yes |
| No | Yes | No |
| Yes | No | No |
| No | No | No |
Now what does this table remind us of? It is precisely the truth table for “and.” It is just what we would have if we wrote down the truth table of the statement “Switch 1 is closed and switch 2 is closed.”

Fig. 2. Switches in parallel.
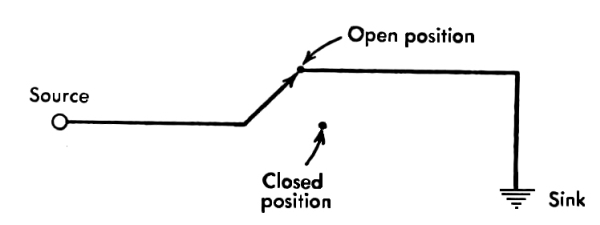
Fig. 3. Switch open—current flowing.
Suppose that we have two switches 1, 2 in parallel (see Fig. 2). When do we get current flowing from the source to the sink? [Pg 155] Answer: when either one or both of the switches are closed. Therefore, this circuit is an exact representation of the statement “Switch 1 is closed or switch 2 is closed.”
Suppose that we have a switch that has two positions, and at any time must be at one and only one of these two positions (see Fig. 3). Suppose that current flows only when the switch is open. There are two possible cases and results (see Table 10).
Table 10
| Switch 1 is closed |
Current flows |
|---|---|
| Yes | No |
| No | Yes |
This is like the truth table for “not”; and this circuit is an exact representation of the statement “Switch 1 is not closed.” (Note: These examples are in substantial agreement with Shannon’s paper, although Shannon uses different conventions.)
We see, therefore, that there is a very neat correspondence between the algebra of logic and automatic switching circuits. Thus it happens that:
1. The algebra of logic can be used in the calculation of some electrical circuits.
2. Some electrical circuits can be used in the calculations of the algebra of logic.
This fact is what led to the next step.
In 1946 two undergraduates at Harvard University, Theodore A. Kalin and William Burkhart, were taking a course in mathematical logic. They noticed that there were a large number of truth tables to be worked out. To work them out took time and effort and yet was a rather tiresome automatic process not requiring much thinking. They had had some experience with electrical circuits. Knowing of Shannon’s work, they said to each other, “Why not build an electrical machine to calculate truth tables?”
They took about two months to decide on the essential design of the machine: [Pg 156]
1. The machine would have dial switches in which logical connectives would be entered.
2. It would have dial switches in which the numbers of statements like 1, 2, 3 ··· would be entered.
3. It would scan the proper truth table line by line by sending electrical pulses through the dial switches.
4. It would compute the truth or falsehood of the whole expression.
With the designs in mind, Kalin and Burkhart bought some war surplus materials, including relays, switches, wires, lights, and a metal box about 30 inches long by 16 inches tall, and 13 inches deep. From March to June, 1947, they constructed a machine in their spare time, assembling and mounting the parts inside the box. The total cost of materials was about $150. In June the machine was demonstrated in Cambridge, Mass., before several logicians and engineers, and in August it was moved for some months to the office of a life insurance company. There some study was made of the possible application of the machine in drafting contracts and rules.
The logical-truth calculator built by Kalin and Burkhart is not giant in size, although giant in capacity. Like other mechanical brains, the machine is made up of many pieces of a rather small number of different kinds of parts. The machine contains about 45 dial switches, 23 snap switches (or two-position switches), 85 relays, 6 push buttons, less than a mile of wire, etc. The lid of the metal box is the front, vertical panel of the machine.
The machine contains 16 units. These units are listed in Table 11, in approximately the order in which they appear on the front panel of the machine—row by row from top to bottom, and from left to right in each row. [Pg 157]
Table 11
| UNITS, THEIR NAMES, AND SIGNIFICANCE | ||||||
|---|---|---|---|---|---|---|
| Unit | Row | Part | No. | Mark | Name | Significance |
| 1 | 1 | Small red lights |
12 | — | Statement truth- value lights |
Output: glows if statement is assumed true in the case |
| 2 | 1 | 2-position snap switches |
12 | ~ | Statement denial switches |
Input: if up, statement is denied |
| 3 | 2 | 14-position dial switches |
12 | V | Statement switches |
Input of statements |
| 4 | 3 | 4-position dial switches |
11 | k | Connective switches |
Input of connectives: ∧ (and), ∨ (or), ▲ (if-then), ▼ (if and only if) |
| 5 | 4 | 11-position dial switches |
11 | A | Antecedent switches |
Input of antecedents |
| 6 | 5 | 11-position dial switches |
11 | C | Consequent switches |
Input of consequents |
| 7 | 6 | 2-position snap switches |
11 | S | Stop switches | Input: if up, associates connective to main truth-value light |
| 8 | 6 | 2-position snap switches |
11 | ~ | Connective denial switches |
Input: if up, statement produced by connective is denied |
| 9 | 7 | Red light and large button |
1 | Start | Automatic start | Input: causes the calc. to start down a truth table automatically |
| 10 | 7 | Red light and 2 buttons |
1 | Start Stop |
Power switch | Input: turns the power on or off |
| 11 | 7 | 2-position snap switch and red button |
1 | Stop | “Stop-on-true-or- false” switch |
Input: causes the calc. to stop either on true cases or on false cases |
| 12 | 7 | Yellow light | 1 | — | Main truth-value light |
Output: glows if the statement produced by the main connective is true for the case |
| 13 | 7 | Large button | 1 | Man. Pulse |
Manual pulse button |
Input: causes the calc. to go to the next line of a truth table |
| 14 | 7 | 11-position dial switch |
1 | kⱼ | Connective check switch and light |
Output: glows when any specified connective is true |
| 15 | 7 | 13-position dial switch |
1 | TT Row Stop |
“Truth-table-row- stop” switch |
Input: causes the calc. to stop on the last row of the truth table |
| 16 | Be- tween 6 & 7 |
Continuous dial knob and button |
1 | — | Timing control knob |
Input: controls the speed at which the calculator scans rows of the truth table |
[Pg 158] Some of the words appearing in this table need to be defined. Connective here means “and,” “or,” “if ··· then,” “if and only if.” Only these four connectives appear on the machine; others when needed can be constructed from these. The symbols used for these connectives in mathematical logic are ∧, ∨, ▲, ▼. These signs serve as labels for the connective switch points. In this machine, when there is a connective between two statements, the statement that comes before is called the antecedent and the statement that comes after is called the consequent.
Of the 16 units 13 are input units. They control the setup of the machine so that it can solve a problem. Of the 13 input units, those that have the most to do with taking in the problem are shown in Table 12.
Table 12
| Unit | Name of Switches |
Mark | Kind of Switch |
Switch Settings |
|---|---|---|---|---|
| 3 | Statement | V₁ to V₁₂ |
Dial | Statements 1 to 12 or constant T or F |
| 2 | Statement denial |
~ | Snap | Affirmative (down) or negative (up) |
| 4 | Connective | k₁ to k₁₁ |
Dial | ∧ (and), ∨ (or), ▲ (if-then), ▼ (if and only if) |
| 8 | Connective denial |
~ | Snap | Affirmative (down) or negative (up) |
| 5 | Antecedent | A₁ to A₁₁ |
Dial | V or various k’s |
| 6 | Consequent | C₁ to C₁₁ |
Dial | V or various k’s |
| 7 | Stop | S₁ to S₁₁ |
Snap | Not connected (down) or connected (up) |
The first step in putting a problem on the machine is to express the whole problem as a single compound statement that we want to know the truth or falsity of. We express the single compound statement in a form such as the following:
V k V k V k V k V k V k V k V k V k V k V k V
[Pg 159] where each V represents a statement, each k represents a connective, and we know the grouping, or in other words, we know the antecedent and consequent of each connective.
For example, let us choose a problem with an obvious answer:
Problem. Given: statement 1 is true; and if statement 1 is true, then statement 2 is true; and if statement 2 is true, then statement 3 is true; and if statement 3 is true, then statement 4 is true. Is statement 4 true?
How do we express this whole problem in a form that will go on the machine? We express the whole problem as a single compound statement that we want to know the truth or falsity of:
If [1 and (if 1 then 2) and (if 2 then 3) and (if 3 then 4)], then 4
The 8 statements occurring in this problem are, respectively: 1 1 2 2 3 3 4 4. These are the values at which the V switches (the statement dial switches, Unit 2) from V₁ to V₈ are set. The 7 connectives occurring in this problem are, respectively: and, if-then, and, if-then, and, if-then, if-then. These are the values at which the k switches (the connective dial switches, Unit 4) from k₁ to k₇ are set.
A grouping (one of several possible groupings) that specifies the antecedent and consequent of each connective is the following:
| 1 | and | 1 | if-then | 2 | and | 2 | if-then | 3 | and | 3 | if-then | 4 | if-then | 4 |
| | | | | | | | | | | | | |||||||||
| k₂ | k₄ | k₆ | ||||||||||||
| | | | | | | | | |||||||||||
| k₁ | k₅ | |||||||||||||
| | | | | |||||||||||||
| k₃ | ||||||||||||||
| | | | | |||||||||||||
| k₇ | ||||||||||||||
The grouping has here been expressed graphically with lines but may be expressed in the normal mathematical way with parentheses and brackets as follows: [Pg 160]
{[ 1 and (1 if-then 2)] and [(2 if-then 3) and (3 if-then 4) ] } if-then 4.
So the values at which the antecedent and consequent dial switches are set are as shown in Table 13.
Table 13
| Connective | Antecedent Switch |
Set at | Consequent Switch |
Set at |
|---|---|---|---|---|
| k₁ | A₁ | V | C₁ | k₂ |
| k₂ | A₂ | V | C₂ | V |
| k₃ | A₃ | k₁ | C₃ | k₅ |
| k₄ | A₄ | V | C₄ | V |
| k₅ | A₅ | k₄ | C₅ | k₆ |
| k₆ | A₆ | V | C₆ | V |
| k₇ | A₇ | k₃ | C₇ | V |
In any problem, statements that are different are numbered one after another 1, 2, 3, 4 ···. A statement that is repeated bears always the same number. In nearly all cases that are interesting, there will be repetitions of the statements. If any statement appeared with a “not” in it, we would turn up the denial switch for that statement (Unit 2).
The different connectives available on the machine are “and,” “or,” “if ··· then,” “if and only if.” If a “not” affected the compound statement produced by any connective, we would turn up the denial switch for that connective (Unit 8).
The last step in putting the problem on the machine is to connect the main connective of the whole compound statement to the yellow light output (Unit 12). In this problem the last “if-then,” k₇, is the main connective, the one that produces the whole compound statement. So we turn Stop Switch 7 (in Unit 7) that belongs to k₇ into the up position. There are a few more things to do, naturally, but the essential part of putting the information of the problem into the machine has now been described.
Of the 16 units listed in Table 11, 3 are output units, and only 2 of these are really important, as shown in Table 14. [Pg 161]
Table 14
| Unit | Name of Light | Mark | Kind of Light |
|---|---|---|---|
| 1 | Statement truth value | V₁ to V₁₂ | Small, red |
| 13 | Main truth value | Large, yellow |
The answer to a problem is shown by a pattern of the lights of Units 1 and 13. The pattern of lights is equivalent to a row of the truth table. Each little red light (Unit 1) glows when its statement is assumed to be true, and it is dark when its statement is assumed to be false. The yellow light (Unit 13) glows when the whole compound statement is calculated to be logically true, and it is dark when the whole compound statement is calculated to be logically false.
The machine turns its “attention” automatically to each line of the truth table one after the other, and pulses are fed in according to the pattern of assumed true statements. We can set the machine to stop on true cases or on false cases or on every case, so as to give us time to copy down whichever kind of results we are interested in. When we have noted the case, we can press a button and the machine will then go ahead searching for more cases.
The reader may still be wondering when he will see a complete and concrete example of the application of the logical-truth calculator. So far we have given only pieces of examples in order to illustrate some explanation. Therefore, let us consider now the following problem:
Problem. The A. A. Adams Co., Inc., has about 1000 employees. About 600 of them are insured under a contract for group insurance with the I. I. Insurance Co. Mr. Adams decides that more of his employees ought to be insured. As a part of his study of the change, he asks his manager in charge of the group insurance plan, “What are the possible statuses of my employees who are not insured?”
The manager replies, “I can tell you the names of the men who are not insured, and all the data you may want to know about them.”
Mr. Adams says, “No, John, that won’t be enough, for I need to know whether there are any groups or classes that for some basic reason I should exclude from the change I am considering.”
[Pg 162] So the manager goes to work with the following 5 statuses and the following 5 rules, and he produces the following answer. Our question is, “Is he right, or has he made a mistake?”
Statuses. A status for any employee is a report about that employee, answering all the following 5 questions with “yes” or “no.”
1. Is the employee eligible for insurance?
2. Has the employee applied for insurance?
3. Has the employee’s application for insurance been approved?
4. Does the employee require a medical examination for insurance?
5. Is the employee insured?
Rules. The rules applying to employees are:
A. Any employee, to be insured, must be eligible for insurance, must make application for insurance, and must have such application for insurance approved.
B. Only eligible employees may apply for insurance.
C. The application of any person eligible for insurance without medical examination is automatically approved.
D. (Naturally) an application can be approved only if the application is made.
E. (Naturally) a medical examination will not be required from any person not eligible for insurance.
Answer by the Manager. There are 5 possible combinations of statuses for employees who are not insured, as shown in Table 15.
Table 15
| Possible Combination of Statuses |
Status 1, Eligible |
Status 2, Applied |
Status 3, Application Approved |
Status 4, Examination Required |
Status 5, Insured |
|---|---|---|---|---|---|
| 1 | Yes | Yes | Yes | Yes | No |
| 2 | Yes | Yes | Yes | No | No |
| 3 | Yes | Yes | No | Yes | No |
| 4 | Yes | No | Yes | No | No |
| 5 | No | No | No | No | No |
The question may be asked why employees who are eligible, who have applied for insurance, who have had their applications approved, and who require no medical examination (combination 2) are yet not insured. The answer is that the rules given do not logically lead to this conclusion. As a matter of fact, there might be additional rules, such [Pg 163] as: any sick employee must first return to work; or any period from date of approval of application to the first of the following month must first pass.
The first step in putting this problem on the Kalin-Burkhart Logical-Truth Calculator is to rephrase the rules, using the language of the connectives that we have on the machine. The rules rephrased are:
A. If an employee is insured, then he is eligible, he has applied for insurance, and his application has been approved.
if 5, then 1 and 2 and 3
B. If an employee has applied (under these rules) for insurance, then he is eligible.
if 2, then 1
C. If an employee is eligible for insurance, has applied, and requires no medical examination, his application is automatically approved.
if 1 and 2 and not-4, then 3
D. If an employee’s application has been approved, then he has applied.
if 3, then 2
E. If an employee is not eligible, then he does not require a medical examination (under these rules).
if not-1, then not-4
To get the answer we seek, we must add one more rule for this answer only:
F. The employee is not insured.
not-5
We now have a total of 4 + 2 + 4 + 2 + 2 + 1 occurrences of statements, or 15 occurrences. This is beyond the capacity of the existing machine. But fortunately Rule F and Rule A cancel each other; they may both be omitted; and this gives us 10 occurrences instead of 15. In other words, all the possible statuses under “Rule B and Rule C and Rule D and Rule E” will give us the answer we seek.
The rephrasing and reasoning we have done here is perhaps not easy. For example, going from the logical pattern
Only igs may be ows
to the logical pattern [Pg 164]
If it is an ow, then it is an ig
as we did in rephrasing Rule B, deserves rather more thought and discussion than we can give to the subject here. A person who is responsible for preparing problems for the Logical-Truth Calculator should know the algebra of logic.
Choosing an appropriate grouping, we now set on the machine:
{(if 2, then 1) and [IF (1 and 2) and not-4, then 3]} and
[(if 3, then 2) and (IF not-1, then not-4)]
The setting is as shown in Table 16. After this setting, the machine is turned on and set to stop on the “true” cases. The
Table 16
SETTING OF THE PROBLEM
ON THE
LOGICAL-TRUTH CALCULATOR
| Unit | |||||||||||||
| 3 | Statement Dial No. | V₁ | V₂ | V₃ | V₄ | V₅ | V₆ | V₇ | V₈ | V₉ | V₁₀ | V₁₁ | V₁₂ |
| 3 | Statement Dial Setting | 2 | 1 | 1 | 2 | 4 | 3 | 3 | 2 | 1 | 4 | F | F |
| 2 | Statement Denial Switch | ||||||||||||
| Setting | — | — | — | — | up | — | — | — | up | up | — | — | |
| 4 | Connective Dial No. | k₁ | k₂ | k₃ | k₄ | k₅ | k₆ | k₇ | k₈ | k₉ | k₁₀ | k₁₁ | |
| 4 | Connective Dial Setting | ▲ | ∧ | ∧ | ∧ | ▲ | ∧ | ▲ | ∧ | ▲ | off | off | |
| 8 | Statement Denial Switch | ||||||||||||
| Setting | — | — | — | — | — | — | — | — | — | — | — | ||
| 5 | Antecedent Dial No. | A₁ | A₂ | A₃ | A₄ | A₅ | A₆ | A₇ | A₈ | A₉ | A₁₀ | A₁₁ | |
| 5 | Antecedent Dial Setting | V | k₁ | V | k₃ | k₄ | k₂ | V | k₇ | V | off | off | |
| 6 | Consequent Dial No. | C₁ | C₂ | C₃ | C₄ | C₅ | C₆ | C₇ | C₈ | C₉ | C₁₀ | C₁₁ | |
| 6 | Consequent Dial Setting | V | k₅ | V | V | V | k₈ | V | k₉ | V | off | off | |
| 7 | Stop Switches, associating | ||||||||||||
| connective to Main | |||||||||||||
| Truth-Value Light | — | — | — | — | — | — | — | — | — | — | — | ||
possible statuses of employees who are not insured are shown in Table 17. As we look down the last column in Table 17, we observe 6 occurrences of T, instead of 5 as the manager determined (see Table 15). Thus, when we compare the manager’s result with the machine result, we find an additional possible combination to be reported to Mr. Adams, combination 7:
Employee eligible, employee has not applied, employee’s application not approved, employee requires a medical examination, employee not insured.
[Pg 165]
Table 17
SOLUTION OF THE PROBLEM
BY THE CALCULATOR
| {A} | {B} | {C} | {D} | {E} | {F} | {G} | ||
|---|---|---|---|---|---|---|---|---|
| Status: | 1 | 2 | 3 | 4 | 5 | |||
| T | T | T | T | F | 1 | T | ||
| F | T | T | T | F | 2 | F | ||
| T | F | T | T | F | 3 | F | ||
| F | F | T | T | F | 4 | F | ||
| T | T | F | T | F | 5 | T | ||
| F | T | F | T | F | 6 | F | ||
| T | F | F | T | F | 7 | T | ||
| F | F | F | T | F | 8 | F | ||
| T | T | T | F | F | 9 | T | ||
| F | T | T | F | F | 10 | F | ||
| T | F | T | F | F | 11 | F | ||
| F | F | T | F | F | 12 | F | ||
| T | T | F | F | F | 13 | F | ||
| F | T | F | F | F | 14 | F | ||
| T | F | F | F | F | 15 | T | ||
| F | F | F | F | F | 16 | T |
Because of the medical examination, this additional class of employee would need to be considered rather carefully in any change of the group insurance plan.
In appraising the Kalin-Burkhart Logical-Truth Calculator, we must remember that this is a first model. It was the only machine of its kind up to the end of 1948; and it worked.
The cost of the machine, as stated before, was about $150 of parts and perhaps $1000 of labor. This is less than ¹/₁₀₀ of the cost of the [Pg 166] other giant brains described in previous chapters. Yet we can properly call this machine a mechanical brain because it transfers information automatically from one part to another of the machine, has automatic control over the sequence of operations, and does certain kinds of reasoning.
The machine is swift. It can check up to a 100 cases against a set of rules in less than 1 minute. It can check: 128 cases for 7 conditions in 1¼ minutes, 256 cases for 8 conditions in 2½ minutes, and 4096 cases for 12 conditions in 38 minutes. That is the limit of the present machine. Of course, setting up the machine to do a problem takes some more time.
The programming of this machine to do a problem is less complicated than the programming of most of the big machines previously described. Of course, in order to prepare a problem for the machine, the preparer needs to know a fair amount of the algebra of logic. This, however, is not very hard. As to reliability, the machine has in practice been out of order less than 2 per cent of operating time.
The big barrier to wide use of the machine, of course, is lack of understanding of the field of problems in which it can be applied. Even in this modern world of ours, we are in rather a primitive stage in regard to recognizing problems in logical truth and knowing how to calculate it. Here, however, is an electrical instrument for logical reasoning, and it seems likely that its applications will multiply.
[Pg 167]
In the previous chapters we have described four giant mechanical brains finished by the end of 1946: Massachusetts Institute of Technology’s Differential Analyzer No. 2, Harvard’s IBM Automatic Sequence-Controlled Calculator, Moore School of Electrical Engineering’s Electronic Numerical Integrator and Calculator (Eniac), and Bell Telephone Laboratories’ General-Purpose Relay Computer. All these brains have actually worked long enough to have demonstrated thoroughly some facts of great importance.
The existing mechanical brains have proved that information can be automatically transferred between any two registers of a machine. No human being is needed to pick up a physical piece of information produced in one part of the machine, personally move it to another part of the machine, and there put it in again. We can think of a mechanical brain as something like a battery of desk calculators or punch-card machines all cabled together and communicating automatically.
The existing mechanical brains have also proved that flexible, automatic control over long sequences of operations is possible. We can lay out the whole routine to solve a problem, translate it into machine language, and put it into the machine. Then we press the “start” button; the machine starts whirring and prints out the answers as it obtains them. Mechanical brains have removed the limits on complexity of routine: the machine can carry out a complicated routine as easily as a simple one. [Pg 168]
The existing giant brains have shown that a machine with hundreds of thousands of parts will work successfully. It will operate accurately, it will run unattended, and it will have remarkably few mechanical troubles.
These machines have shown that enormous speeds can be realized: 5000 additions a second is Eniac’s record. High speed is needed for many problems in science, government, and business. In fact, there are economic and statistical problems, now settled by armchair methods, for which high-speed mechanical brains may make it possible to compute answers rather than guess them.
Also, these machines have been shown to be reasonable in cost. The cost of each of the large calculators is in the neighborhood of $250,000 to $500,000. If we assume a ten-year life, which is conservative, the cost is about $3 to $6 an hour for 24-hour operation. Since each mechanical brain can, for problems for which it is suited, do the work of a hundred human computers, such a machine can save its cost half a dozen times. And these machines are only engineers’ models, built without the advantages of production-line assembly.
The cost of giant mechanical brains under design in 1947 and 1948 is in the neighborhood of $100,000 to $200,000. The main reason for the reduction from the previous cost is the use of cheaper automatic memory. As designs improve and charges for research and development are paid off, the cost should continue to go down.
In the laboratories working on new mechanical and electronic brains, scientists are doing a lot of thinking about new devices for handling information. Research into devices for storing information shows that magnetic wire as used in sound recording is a rather good storage medium.
For example, on a hundredth of an inch of fine steel wire we can “write” a magnetized spot by means of a small “writing” electromagnet. The electromagnet is simply some copper wire [Pg 169] coiled around some soft iron shaped in a U. When current flows through the coil, the iron becomes a magnet, and the tips of the U magnetize the little section of the wire between them. The magnetized spot can be of two kinds, say north-south or south-north, depending on which way the current flows. We can “read” this difference by means of another small “reading” electromagnet. We can erase the spot by means of a stronger “erasing” magnet that produces a uniform magnetic state throughout the wire. The difference between north-south and south-north corresponds to the difference between 1 and 0, or “yes” and “no,” etc., and is a unit of information (see Chapter 2). Many other variations are possible. For example, the presence or absence of a magnetized spot may be the unit of information, or the “writing,” “reading,” and “erasing” electromagnets all may be the same.
Magnetic wire sound recordings made in the 1890’s are still good. This fact shows that magnetic wire may be a more permanent medium for storing information than is paper. Stray magnetic forces are likely to have no harmful effect on information stored on magnetic wire, for these forces would not be strong enough or detailed enough to change greatly the difference between the magnetized spot and its neighboring neutral area.
A reel of magnetic wire a mile long and ³/₁₀₀₀ of an inch thick costs about $5. At 80 magnetized spots to the inch, a mile of wire can store about 5 million units of information. Hence, the cost of storing one unit of information is about ¹/₁₀₀₀₀ of a cent. The time needed for changing a magnetized spot from 1 to 0 or from 0 to 1 is about ¹/₁₀₀₀₀ of a second.
There is, however, a storage device that may be even more useful, and this is magnetic tape (see Fig. 1). The usual size of such tape is ¼ inch wide and 2 or 3 thousandths of an inch thick. Magnetic tape may be made of plastic with magnetic powder all through it, or it may be of paper coated with magnetic powder, or it may be of stainless steel or a magnetic alloy, or it may be of brass or a nonmagnetic alloy coated with a magnetic plating. [Pg 170]
Magnetic tape has the added advantage that from 4 to 20 channels across the tape can be filled with magnetized spots, and the cost then becomes about ¹/₁₀₀₀₀₀ of a cent per spot. It seems possible that 1000 units of information can be stored in a quarter of a square inch of magnetic tape. This means that more than 1 million units of information can be stored in a cubic inch of space filled with magnetic tape, and about 2 billion units of information in a cubic foot, except that some of the space should be allotted to the reels and other equipment that hold the tape (see Fig. 2). This is closer packing than printed information in the telephone book, and yet with magnetic tape we can get to the information automatically.
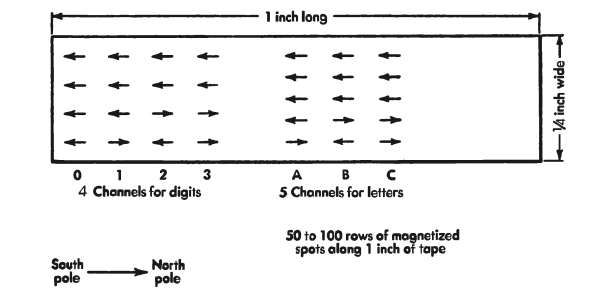
Fig. 1. Magnetic tape.

Fig. 2. Tape reels.
Think of the enormous files in libraries, government, and business. [Pg 171] Think of the problems of space and cost and access which these files imply. We can then see that this new development may well be of extraordinary importance.
Fig. 3. Mercury tank.
Scientists are investigating other storage devices having still more remarkable properties, but these have the disadvantage that, when the power goes off, the information vanishes. One of these new storage devices is called a mercury tank (see Fig. 3). It consists mainly of a section of iron or steel pipe filled with mercury. At each end of this pipe, touching the mercury, is a thin slab of a crystal of quartz. Quartz, which is a common stone, and which nearly all sand is made of, changes its shape when pulsed with electricity. We put a pattern of electrical pulses into the quartz slab at one end of the mercury tank; for example, we could have the pattern 1101 meaning “pulse, pulse, no pulse, pulse.” The electrical pulses going into the quartz slab make the quartz vibrate. Thus ripples are produced in the mercury, and waves in the pattern 1101 meaning “wave, wave, no wave, wave” travel down the tank and strike the quartz slab at the far end. The quartz slab there changes its shape in the rhythm 1101, and it converts the waves back into electrical pulses in the same pattern. Then we take the pulses out of the far end along a wire, make them stronger again with an amplifier, give them the right form again, and feed them back into the front end of the mercury tank. The mercury tank is a clever use of the principle of an echo, as when you call across a valley and the rocks answer you back. We can store a pattern of 400 pulses (each a unit of information, a 1 or a 0, and each a [Pg 172] millionth of a second in duration), in a mercury tank about 20 inches long. A mercury tank and an echo are examples of delay lines—“lines” along which waves are “delayed.”
Another of the memory devices being developed is called an electrostatic storage tube (see Fig. 4). This is a big electronic tube with a screen across one end. The screen may be of two layers: one of copper, which conducts electricity, and one of mica, a material that does not. In the other end of the tube is a beam of electrons, which we can turn on and off and shoot at any of 2 or 3 thousand specific points or spots on the screen.
Fig. 4. Electrostatic storage tube.
There are two sizes of electric charge or quantity of electrons; we can call these 1 and 0. In about a millionth of a second, we can put either size of charge on one of the spots of the screen. With other circuits we can keep it there as long as we want, if the power does not flicker off. We can “remember” perhaps 2 or 3 thousand units of information in one of these electronic tubes. We can read, write, or erase any unit of information in a few millionths of a second.
Neither the mercury tank nor the electrostatic storage tube had, by the end of 1947, been put into a working mechanical brain. But there is good reason to believe that they will be successful devices and will open up a new era of speed in storing and referring to information. In [Pg 173] fact, several laboratories are developing electronic calculating circuits using these devices which will perform up to 100,000 additions a second or 10,000 multiplications a second. Our minds certainly stagger at the thought of such speeds.
Many kinds of combining operations have already been built into one or more mechanical brains. The operations may be arithmetical: addition, subtraction, multiplication, division, looking up numbers in tables, etc. Or the operations may be logical: comparing, selecting, checking, etc. Additional logical operations will be built into some of the mechanical brains now being constructed: sorting, collating, matching, merging, etc.
Programming—the way to give instructions to machines—is also being studied in the laboratories. Several new ideas of importance have developed as a result.
One idea is that the machine should be able to store its instructions or program or routine in its memory in just the same physical ways as it stores numbers. There is basically no reason why numbers only should be stored in some registers, and instructions only stored in other registers.
Another idea is that the machine should have in its permanent memory any subroutine it may need. For example, a subroutine should always be available in the machine for finding square root. At any time when a square root was needed, we would only have to call on the machine for the subroutine of square root. The machine would then consult the right part of its memory and carry out the subroutine for square root.
A third idea, and one of the most interesting, is that the machine should be able to compute its own instructions. For example, consider a program for finding the product of two matrices (see Supplement 2), each of 100 terms in an array of 10 columns and 10 rows, resulting in a new matrix of 100 terms. The whole program can be made to consist of about 50 orders. Only one of them is “multiply,” and only [Pg 174] one of them is “add”; the other orders consist of how to choose expressions to be multiplied or added, etc.
Such problems as these are often fascinating to mathematicians, who love to play with the intricate ideas needed.
Reliability has a number of aspects:
For example, Bell Laboratories proved that mechanical brains can be built so that no wrong results are allowed to come out. In other words, the machine checks itself all the time as it goes along and stops at once if the check shows that something is wrong. This is likely to be a standard feature of new automatic thinking machinery.
The frequency of failures in the machinery being designed in the laboratories may be of the order of one or two mechanical failures a week. For any type of failure an alarm circuit and trouble lights will show what part of the machine needs attention. Plug-in parts for replacement are already in use in at least two of the four mechanical brains described and should be available in all the new machines. It is possible to build a machine that will automatically change from failing equipment to properly functioning equipment. For some years though, this may be too expensive to be reasonable.
The use of magnetic tape for storage reduces greatly the number of parts and so increases reliability. For example, instead of 18,000 electronic tubes in an electronic brain, there may be less than 3000.
A final degree of reliability is gained when most of the time the machine operates unattended. Then, there is no human operator standing by who may fail to do the correct thing at the moment when the machine [Pg 175] needs some attention. In fact, the motto for the room housing a mechanical brain should become, “Don’t think; let the machine do it for you.” Unattended operation from the end of one working day to the beginning of the next, with the machine changing itself from one problem to another problem, has already been proved possible on the Bell Laboratories machine.
In order to use a mechanical brain, we have to give it and take from it language that it understands, machine language. A mechanical brain that can do 10,000 additions a second can very easily finish almost all its work at once. How can we, slow as we are, keep our friend, the giant brain, busy? We have found so far several answers to this question, none of them yet very good.
Devices for preparing input will be very important. For each brain, we shall need a great many of these devices. For, at best, we type at a rate, say, of 4 characters a second, selecting any one of some 38 keys, each of which is equivalent to about 6 units of information. This is about 800 units of information per second. The machine, however, is likely to be able to gulp information from its input mechanism at the amazing rate of 60,000 units of information per second, equal to 75 people typing with no mistakes and no resting. Fortunately, at least some of the time the machine will be busy computing!
For an input-preparation device, we may get something that can be fastened to an ordinary typewriter and that will produce magnetic tape agreeing with what is printed by the typewriter. Since the input information must be carefully verified, we shall need a second magnetic tape device such as exists for paper tape on the Bell Laboratories machine: the processor. The processor takes two hand-prepared tapes, compares them, reports any differences, and produces a third tape. The third tape copies the two original tapes if they agree, and it receives corrected information as furnished by a girl at a keyboard if the two original tapes disagree.
For information already on punch cards, we need an input device that [Pg 176] will read punch cards and write on magnetic tape. Where information is on punched paper tape, we need a machine that will read punched paper tape and write on magnetic tape.
Problem data, tables of numbers, and routine instructions will go into the mechanical brain. They will all be prepared on regular input devices. The machine will accept information in the form in which it is most convenient for you and me to prepare it. Then, the machine will be instructed to change the information into the form with which it is most convenient for the machine to operate.
Many output devices will also be needed, since the machine will be able to produce information very swiftly. These output devices might be cabled to the machine. A kind of traffic control system would govern them. Each will have a magnetic tape that will be loaded up swiftly with information. Then the output device will unload its information more slowly, in any form that we may desire: printing, graphs, film, punch cards, or punched paper tape.
The machine is likely to be able to put out information on magnetic tape at the same high speed of 60,000 units of information per second or 10,000 characters per second. But the best printing speed of an electric typewriter is about 10 or 12 characters a second. Card-punching speed is about 130 characters a second. Punch-card tabulator speed can reach a maximum of about 200 characters a second. Thus we see that here, too, we may be snowed under with the information that the giant brain puts out, if we fail to ask the giant only for what we really want.
This chapter would not be complete without mention of the great mechanical brains that were actually under construction at the end of 1947. In power they are intermediate between the machinery now being designed, described in this chapter, and the earlier machines described in the previous chapters of this book.
The mechanical brains under construction on December 31, 1947, were: [Pg 177]
Harvard’s Sequence-Controlled Relay Calculator Mark II, constructed at the Harvard Computation Laboratory, tested there July 1947 to January 1948, and delivered to the Naval Proving Ground, Dahlgren, Va., in 1948.
The IBM Selective-Sequence Electronic Calculator, constructed in the IBM laboratories, Endicott, N. Y., and installed in 1947 at the office of International Business Machines, 590 Madison Ave., New York, N. Y.
Moore School of Electrical Engineering’s EDVAC (Electronic Digital Variable Automatic Computer) being constructed partly at Moore School and partly elsewhere, and to be delivered to the Ballistic Research Laboratories, Aberdeen, Md.
Harvard’s Sequence-Controlled Electronic Calculator Mark III, being constructed at the Harvard Computation Laboratory, and to be delivered to the Naval Proving Ground, Dahlgren, Va.
We shall cover briefly (and perhaps a little technically) some of the main features of the first two of these machines; for, during 1948, they began to do problems. The other two had not been finished by the end of 1948 and so would be difficult to describe correctly, for mechanical brains grow, and design changes go on until they are finished—and even afterwards.
Some information about these machines can be obtained from the organizations referred to above and from reports that should appear from time to time in some of the journals mentioned in Supplement 3. There is also a regular section entitled “Automatic Computing Machinery” in the quarterly Mathematical Tables and Other Aids to Computation, where it is likely that current information may be found.
The Harvard Sequence-Controlled Calculator Mark II began to do problems under test during July 1947. This machine is at least twelve times as powerful as Mark I (see Chapter 6) and was constructed entirely by the Harvard Computation Laboratory. The machine contains about 13,000 relays of a new type that will operate reliably within ¹/₁₀₀ of a second.
Numbers in the machine are regularly of 10 decimal digits between [Pg 178] 1.000,000,000 and 9.999,999,999, inclusive, multiplied by a power of 10 between 1,000,000,000,000,000 and 0.000,000,000,000,001, inclusive.
For storage of numbers, the machine has 100 relay registers totaling about 1200 decimal digits. Also, it can consult any one of 8 tape feeds for numbers and any one of 4 tape feeds for instructions. Effectively, the machine can read one number and one instruction from paper tape in ¹/₃₀ of a second.
The machine performs all arithmetical and most logical operations. In every second it can carry out 4 multiplications, 8 additions (or subtractions), and 12 transfers. Division is performed by rapid approximation using the other operations.
In each second the machine can perform 30 instructions. An instruction is expressed by 6 digits between 0 and 7 which you can select and, in effect, by 3 more digits fixed by the time (within the second) when the machine reads the instruction. For example, in the 9th instruction of the 30 instructions in each second, we can specify a multiplicand. But, if we do not want to multiply right then—a rare event if we are coding wisely—we leave the 9th instruction empty. The machine may operate as a whole, attending to one problem; or the machine may be separated into halves, and each half will attend to its own problem.
The IBM Selective-Sequence Electronic Calculator was announced publicly on January 27, 1948, after some months of trial running. It is a large and powerful mechanical brain, and it is the intention of International Business Machines to devote it to solving scientific problems. The staff of the Watson Scientific Computing Laboratory in New York will be mainly in charge of the machine.
The machine contains about 12,500 electronic tubes and about 21,500 relays. Numbers in the machine are regularly of either 14 or 19 decimal digits. Instructions are expressed as numbers. For storage of information, the machine has a capacity of 8 registers totaling 160 decimal digits of very rapid memory in electronic tubes. Also, it has about 150 registers totaling 3000 decimal digits of less rapid memory in relays. Also, it can consult any one of 66 paper tape feeds; each [Pg 179] row on a paper tape can hold up to 78 punched holes or 19 decimal digits, and the machine can consult 25 rows on one tape in one second. These paper tapes together give the machine about 400,000 decimal digits of memory.
For arithmetical and logical operations, the machine has an arithmetical unit using electronic tubes. This unit can carry out about 50 multiplications or about 250 additions per second, including the transfers of numbers. In each second the machine can read and perform 50 instructions, and each instruction consists, usually, of getting two numbers out of two relay registers, performing an operation, and putting the result into a third relay register.
As this book went to press, another mechanical brain, the Electronic Binary Automatic Computer, or BINAC, was announced on August 22, 1949. This machine was constructed by the Eckert-Mauchly Computer Corporation, Philadelphia, Pa., for Northrop Aircraft, Inc., Hawthorne, Calif.
This machine has some remarkable properties. It does addition or subtraction at the rate of 3500 per second. It does multiplication or division at the rate of 1000 per second. The input is from a keyboard or magnetic tape; the output is to magnetic tape or an electric typewriter. Binac has 512 registers of very rapid memory in mercury tanks, and each register holds 30 binary digits. The machine actually is a pair of twins: the storage, the computing element, and the control are double, and each twin runs in step with the other and checks every operation of the other. In tests in July the machine ran over 10 consecutive hours with no error. Each twin has only 700 electronic tubes. Binac handles all numbers in binary notation, except that the keyboard and the typewriter express numbers in octal notation (see Supplement 2). Finally, Binac is only 5 feet high, 4 feet long, and one foot wide.
[Pg 180]
The pen is mightier than the sword, it is often said. And if this is true, then the pen with a motor may be mightier than the sword with a motor.
In the Middle Ages, there were few kinds of weapons, and it was easy for a man to protect himself against most of them by wearing armor. As gunpowder came into use, a man could no longer carry the weight of armor that would protect him, and so armor was given up. But in 1917, armor, equipped with a motor and carrying the man and his weapons, came back into service—as the tank.
In much the same way, in the Middle Ages, there were few books, and it was easy for a man to handle nearly all the information that was in books. As the printing press came into use, man’s brain could no longer handle all recorded information, and the effort to do so was given up. But in 1944, a brain to handle information, equipped with a motor and supporting the man and his reasoning, came into existence—as the sequence-controlled calculator.
In previous chapters we have examined some of the giant mechanical brains that have been finished; we have also considered the design of such machines. Now in this chapter we shall discuss the future significance of machines that think, of motorized information. We shall discuss what we can foresee if we look with imagination into the future.
There are two questions we need to ask: What types of machines that think can we foresee? What types of problems to be solved by these machines can we foresee? [Pg 181]
The machines that already exist show that some processes of thinking can already be performed very quickly:
We can expect other processes of thinking to come up to high speed through the further development of thinking machines.
Nowadays when we wish to send out announcements of an event, like going to South America for a year, we may copy the addresses of our friends onto the envelopes by hand. In the future, we can see our address book as a spool of magnetic tape. When we wish to send out announcements, we put a stack of blank envelopes into the machine that will read the magnetic tape, and we press a button. Out will come the envelopes addressed.
If we wish to select only those friends of ours whose last names we put down on a list, we can write the list on another magnetic tape, place it also in the machine, and set a few switches. Then the machine will read the names on the list, find their addresses in the address-book tape, and prepare only the envelopes we want. If a friend’s address changes, we can notify the machine. It will find his old address, erase it, and enter the new address.
We can foresee the development of machinery that will make it possible to consult information in a library automatically. Suppose that you go into the library of the future and wish to look up ways for making biscuits. You will be able to dial into the catalogue machine “making biscuits.” There will be a flutter of movie film in the machine. Soon it will stop, and, in front of you on the screen, will be projected the part of the catalogue which shows the names of three or four books containing recipes for biscuits. If you are satisfied, you will press a [Pg 182] button; a copy of what you saw will be made for you and come out of the machine.
After further development, all the pages of all books will be available by machine. Then, when you press the right button, you will be able to get from the machine a copy of the exact recipe for biscuits that you choose.
We are not yet at the end of foreseeable development. There will be a third stage. You will then have in your home an automatic cooking machine operated by program tapes. You will stock it with various supplies, and it will put together and cook whatever dishes you desire. Then, what you will need from the library will be a program or routine on magnetic tape to control your automatic cook. And the library, instead of producing a pictorial copy of the recipe for you to read and apply, will produce a routine on magnetic tape for controlling your cooking machine so that you will actually get excellent biscuits!
Of course, you may have other kinds of automatic producing machinery in your home or office. The furnishing of routines to control automatic machinery will become a business of importance.
Another machine that we can foresee would be used for translating from one language to any other. We can call it an automatic translator. Suppose that you want to say “How much?” in Swedish. You dial into the machine “How much?” and press the button “Swedish,” and the machine will promptly write out “Hur mycket?” for you. It also will pronounce it, if you wish, for there would be little difficulty in recording on magnetic tape the pronunciation of the word as spoken by a good speaker of the language. The machine could be set to repeat the pronunciation several times so that the student could really learn the sound. He could learn it better, probably, by hearing it and trying to say it than he could by using any set of written symbols.
We now come to a possible machine that uses a new principle. This principle is that of being able to recognize signs. This machine [Pg 183] would perceive writing on a piece of paper and recognize that all the a’s that appear on the paper are cases of a, and that all the b’s that appear on it are instances of b, and so forth. The machine could then control an electric typewriter and copy the marks that it sees. The first stage of this machine would be one in which only printed characters of a high degree of likeness could be recognized. In later stages, handwriting, even rather illegible handwriting, might be recognizable by the machine. We can call it an automatic typist.
The elements of the automatic typist would be the following:
1. Phototubes (electronic tubes sensitive to the brightness of light), which could sense the difference between black and white (these already exist).
2. A memory of the shapes of 52 letters, 10 digits, and punctuation marks. Fine distinctions would be required of this memory in some cases—like the difference between the numeral 5 and the capital letter S.
3. A control that would cause the machine to tune itself, so that a good matching between the marks it observed and the shapes it remembered would be reached.
4. A triggering control so that, when the machine had reached good enough matching between its observations and its memory, the machine would proceed to identify the marks, read them, and transfer them.
5. An electric typewriter, which would respond to the transferred instructions. (This also already exists.)
This machine is perhaps not so farfetched as it might seem. During World War II, gun-aiming equipment using the new technique radar reached a high stage of development. Many shots that disabled and sank enemy ships were fired in total darkness by radar-controlled guns. On the glowing screen in the control room, there were two spots, one that marked the target and one that reported the point at which the gun was aimed. These two spots could be brought almost automatically into agreement. In the same way, a report from a phototube telling the shape of an observed mark and a report from the memory of the machine telling [Pg 184] the shape of a similar mark could be compared by the machine for likeness and, if judged enough alike, could be approved as identical.
Even the phrase “enough alike” can be applied by a machine. During World War II, tremendous advances were made in machinery for deciphering enemy messages. Machines observed various features and patterns in enemy messages, swiftly counted the frequency of these features, and carried out statistical tests. Then the machines selected those few cases in which the patterns showed meaning instead of randomness.
A machine like the automatic typist, if made flexible enough, would be, of course, extremely useful. A great load of dull office work is now being thrown on clerks whose task is to translate from writing and typing into languages that machines can read, such as punch cards. At the present time, if punch-card machines are widely used in a big company, the company must employ large numbers of girls whose sole duty is to read papers and punch up cards. A still bigger chore is the work of typists in all kinds of businesses whose main duty is to read handwriting, etc., and then copy the words on a typewriter.
Each square in the grill
is watched by a phototube.
Fig. 1. Scheme for distinguishing A and H by 15 phototubes.
Research has already begun on various features of the automatic typist because of its obvious labor-saving value. For example, many patents have been issued on schemes for dividing the area occupied by a letter or a digit into an array of spots, with a battery of phototubes each watching a spot. The reports from the phototubes together will distinguish the letter or digit. For example, if we consider A and H placed in a grill of fifteen spots, 5 long by 3 wide [Pg 185] (see Fig. 1), then the phototubes can distinguish between A and H by sensing black or white in the spot in the middle of the top row. When we consider how easily and swiftly a human being does this, we can once more marvel at the recognizing machine we all carry around with us in our heads.
Another development that we can foresee is one that we can call the automatic stenographer. This is a machine that will listen to sounds and write them down in properly spelled English words. The elements of this machine can be outlined:
1. Microphones, which can sense spoken sounds (these already exist).
2. A memory storing the 40 (more or less) phonetic units or sounds that make up English, such as the 23 consonant sounds,
| p | b | l | ng |
| f | v | m | th |
| t | d | n | r |
| s | z | h | y |
| k | g | w | |
| ch | j | ||
| sh | zh (heard in “pleasure”) | ||
and the 17 vowel sounds,
| Long | Short | Other |
|---|---|---|
| A (“ate”) | a (“cat”) | ar (“are”) |
| E (“eat”) | e (“end”) | aw (“awe”) |
| I (“isle”) | i (“in”) | er (“err”) |
| O (“owe”) | o (“on”) | ow (“owl”) |
| U (“cute”) | u (“up”) | oi (“oil”) |
| OO (“roof”) | oo (“book”) |
3. A collection of the rules of spelling in English, containing many statements like [Pg 186]
The sound b is always spelled b
The sound sh may be spelled sh (ship), s (sugar), ti (station), ci (physician), ce (ocean) or tu (picture) and other statements based on context, word lists, derivation, etc. These are the statements by means of which a good English speller knows how to spell even words that he hears for the first time.
4. A triggering control so that, when the machine reaches good enough matching between its observations of sounds, its memory of sounds, and its knowledge of spelling rules, the machine will identify groups of sounds as words, determine their spelling, and report the letters determined.
5. An electric typewriter, which would type the reported letters.
With this type of machine, you would dictate your letters into a machine (now existing) that would record your voice. Then the record would be placed on the automatic stenographer, and out would come your letters written and spaced as they should be.
We can foresee a recognizing machine with very general powers. Suppose that we call it an automatic recognizer (see Fig. 2). It will have the following elements:
1. Input. This element will consist of a set of observing instruments, capable of perceiving sights, sounds, etc. There will be ways of positioning or tuning these instruments.
2. Memory. This element will store knowledge. It may store the patterns of observations that we are interested in; or it may store general rules on how to find patterns of observations that we will be interested in. It will contain knowledge about acceptable groups of patterns, about actions to be performed in response to patterns, etc. [Pg 187]
3. Program 1. The element “Program 1” performs a set of standard instructions. Under these instructions, the machine:
Compares group after group of observations with the information in the memory.
Compares these groups with patterns furnished, or seeks to organize the observations into patterns.
Counts cases and tests frequencies.
Finds out how much matching with patterns there is.
Tunes the observing instruments in ways to increase matching.
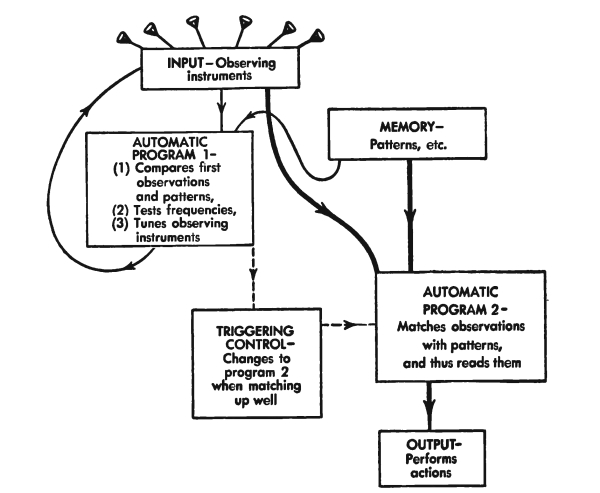
Fig. 2. Scheme of an automatic recognizer.
4. Program 2. The element “Program 2” performs another set of standard instructions. Under these instructions, the machine, if it is tuned well, matches sets of observations one after another with the patterns and so reads them.
5. Triggering Control. This element shifts the control of the machine from Program 1 to Program 2. It does this when the machine reaches “good matching.” We shall set the meaning of this into the machine in much the same way as we set “warm” into a thermostat.
6. Output. This element performs any action that we want, depending on recognized patterns read and any other knowledge or instructions stored in the memory.
[Pg 188] The automatic recognizer will be capable of extraordinary tasks. With microphones and a large memory, this type of machine would be able to hear a foreign language spoken and translate it into spoken or written English. With phototubes and with an expanded filtering and decoding capacity as in deciphering machines, the automatic recognizer should be able to read a dead language, even those (such as Minoan or Etruscan) that have so far resisted efforts to read it. The machine would derive rules for the translation of the language and translate any sample.
An automatic recognizer could perhaps be equipped with many sensitive, tiny observing instruments that could be placed around or in the brain and nervous systems of animals. Then the machine might enable us to find out what activity in the nervous system corresponds with what activity in the animal.
We turn now to the second question regarding the future of machines that think: What types of problems can we foresee as solved by these machines?
Probably the foremost problem which machines that think can solve is automatic control over all sorts of other machines. This involves controlling a machine that is running so that it will do the right thing at the right time in response to information. For example, suppose that you are mowing a lawn with a mowing machine. You watch the preceding strip so as to stay next to it. You watch the ends of the strips, where you turn around. If a stick is caught in the cutting blade, you stop and take it out. Now it is entirely possible to put devices on the mowing machine so that all these things will be taken care of automatically. In fact, in the case of plowing a large field, a tractor-plow can be equipped with a device that guides it next to the preceding furrow. Thus, once the first furrow around the edge has been made, riderless tractors will plow a whole field and stop in the middle. [Pg 189]
For another example, take a gas furnace for heating steam to keep a house warm. Such a furnace has automatic controls, which respond to the following information whenever reported:
In fact, your own meaning of “warm” can be put into the control system: you set the dial on your thermostat at the temperature that “warm” is to be for you.
In the future many kinds of automatic control will be common. We shall have automatic pilots for flying and landing airplanes. We shall have automatic missiles for destructive purposes, such as bombing and killing, and for constructive purposes, such as delivering mail and fast freight. An article in the magazine Fortune for November 1946 described the automatic factory (see Supplement 3). This is a factory in which there would be automatic arms for holding stuff being manufactured, and automatic feed lines for supplying material just where it is needed. All this factory would be controlled by machines that handle information automatically and produce actions that respond to information.
This prospect fills us with concern as well as with amazement. How shall we control these automatic machines, these robots, these Frankensteins? What will there be left for us to do to earn our living? But more of this in the next chapter.
Other problems for which we can foresee the use of machines that think are the understanding, and later the controlling, of nature. One of these problems is weather forecasting and weather control.
We can imagine the following type of machine—a weather brain. [Pg 190] A thousand weather observatories all over the country observe the weather at 8 a.m. The observations are fed automatically through a countrywide network of communication lines into a central station. Here a giant machine, containing a great deal of scientific knowledge about the weather, takes in all the data reported to it. At 8:15 the weather brain starts to calculate; in half an hour it has finished, having produced an excellent forecast of the weather for the whole country. Then it proceeds to transmit its forecast all over the country. By 8:50 every weather station, newspaper, radio station, and airport in the country has the details. In October 1945, Dr. V. K. Zworykin of the Princeton Laboratories of the Radio Corporation of America proposed solving the problem of weather forecasting in this way by a giant brain.
The weather brain will have a second stage of application. From time to time and here and there, the weather is unstable: it can be triggered to behave in one way or another. For example, recently, pellets of frozen carbon dioxide—often called Dry Ice—have been dropped from planes and have caused rain. In fact, a few pounds of Dry Ice have apparently caused several hundred tons of rain or snow. In similar ways, we may, for example, turn away a hail storm so that hail will fall over a barren mountain instead of over a farming valley and thus protect crops. Or we may dispel conditions that would lead to a tornado, thus avoiding its damage. Both these examples involve local weather disturbances. However, even the greatest weather disturbances, like hurricanes and blizzards, may eventually be directed to some extent. Thus the weather may become to some degree subject to man’s control, and the weather brain will be able to tell men where and when to take action.
Another scientific problem to which new machinery for handling information applies is the problem of understanding human beings and their behavior. This increased understanding may lead to much wiser dealing with human behavior.
For example, consider tests of aptitudes. If you take one of these tests, you may be asked to mark which word out of five suggested ones is nearest in meaning to a given word. Or your test may be 40 simple [Pg 191] arithmetical problems to be solved in 25 minutes. Or you may be given a sheet with 20 circles, and be asked to put 3 dots in the first, 7 dots in the second, 4 dots in the third, 11 dots in the fourth, and so on, irregularly; you may be given a total of 45 seconds to do this as well as you can. Now, if a vocational counselor gives you one of these tests, and if you get 84 out of 100 on it, he needs to know just what he has measured about you. Also, he needs to know whether he can reasonably forecast that, as a result of your grade of 84, you will be good at writing articles, or good at supervising the work of other people, or good at designing in a machine shop. He needs to know the records of people with scores of about 84 on this test and to have evidence supporting his forecasts.
If we wish to make the most use of the tests, we need to carry out a good deal of statistics, mathematics, and logic. For example, it will turn out that answers to some questions are much more significant than answers to others, and so we can greatly improve the quality of the tests by keeping only the more significant questions. Powerful machinery for handling calculations will be very useful in the field of aptitude testing.
But, you may ask, what if the person analyzing your answers has to use interpretations and judgments? If the judgments and interpretations can be expressed in words, and if the words can be translated into machine language, then the machine can carry out the analysis. Usually the difference between a rule and a judgment is simply this: a rule in a case in which it is hard to express all the factors being considered is called a judgment.
It is conceivable that machines that think can eventually be applied in the actual treatment of mental illness and maladjustment. Consider what a physician does. In treating a psychiatric case, such as a neurosis, a physician uses words almost entirely. He asks questions. He listens to the patient’s answers. Each answer takes the physician nearer and nearer to a diagnosis. By and by the physician knows what most of the difficulty is. Then he must present his knowledge slowly to the patient, gradually guiding the patient to understanding. It is a psychological truth that telling a man in ten [Pg 192] minutes what is wrong with him does not cure him. The physician seeks to free the patient from the tormenting circles of habit and worry in which he has been trapped. Often the diagnosis is short and the treatment is long; the reasons for the neurosis may soon be clear to the physician, but they may take months to become clear to the patient.
Now let us consider the following kind of machine as an aid to the physician. We might call this kind of machine a psychological trainer, for in many ways it is like the training machines used in World War II for training a pilot to fly an airplane. The psychological trainer would have the following properties:
1. The machine is able to show sound movies—produce pictures and utter words.
2. It is able to put before the patient: situations, problems, questions, experiences, etc.
3. It is able to take in responses from the patient.
4. It is able to receive a program of instructions from the physician.
5. Depending on the responses of the patient and on the program from the physician, the training machine can select more material to put before the patient.
6. The training machine produces a record of what it presented and of how the patient responded, so that the physician and the patient can study the record later.
What sort of films would the machine hold? The machine could be loaded with a number of films which would help in the particular type of neurosis from which the patient was suffering.
What sort of responses could the patient make? The patient might have buttons in front of him which he could press to indicate such answers as:
| Yes | I don’t know | Repeat |
| No | It depends | Go ahead |
Also, the patient might hold a device—like a lie detector, perhaps—which would report his state of tenseness, etc., and so report what he really felt.
Where would the machine’s questions come from? From one or more physicians very clever in the treatment of mental illness. [Pg 193]
Suppose that the patient is inconsistent in his answers? The machine, discovering the inconsistencies, could return to the subject and ask related questions in a different way. As soon as several questions related to the same point are answered consistently, the machine could exclude groups of questions that no longer apply and could proceed to other questions that would still apply.
Patients would vary in their ability to go as fast as the machine could. So from time to time the machine would ask questions to test the effect of what it had presented; and, depending on the answers, the machine would go faster or would bring in additional material to clarify some point.
This machine might have a few advantages over ordinary treatment. For example, with the machine, treatment does not depend on the physician’s making the right answer in a split second, as it may in a personal interview. Also, the patient might be franker with the machine than with the physician, for it might be arranged that the patient could review his record, and then decide whether to confess it to his physician.
Such a machine would enable physicians to treat many more patients than they now can. In fact, it is estimated that nearly 50 per cent of persons who consult physicians are suffering only from mental illness. Such a machine would therefore be a great help.
Another large group of problems for which we can foresee the use of machines that think is found in business and economics.
For example, consider production scheduling in a business or a factory. The machine takes in a description of each order received by the business and a description of its relative urgency. The machine knows (that is, has in its memory) how much of each kind of raw material is needed to fill the order and what equipment and manpower are needed to produce it. The machine makes a schedule showing what particular men and what particular equipment are to be set to work to produce the order. The machine turns out the best possible production schedule, showing who should do what when, so that all the orders will be filled [Pg 194] in the best sequence. What is the “best” sequence? We can decide what we think is the best sequence, and we can set the machine for making that kind of selection, in the same way as we decide what is “warm” and set the thermostat to produce it!
On a much larger scale, we can use mechanical brains to study economic relations in a society. Everything produced in a society is made by consuming some materials, labor, equipment, and skill. The output produced by one man or factory or industry becomes the input for other men, factories, industries. In this way all economic units are linked together by many different kinds and degrees of dependence. The situation is, of course, complicated: it changes as time goes on and as people want different things produced. Economists have already set up simple models of economic societies and have studied them. But with machines that think, it will be possible to set up and study far more complicated models—models that are very much like the society we live in. We can then answer questions of economics by calculation instead of by arguments and counting noses. We shall be able to solve definitely such problems as: “How will a rise in the price of steel affect the farming industry?” “How much money must be paid out as wages and salaries so that consumer purchasing power will buy back what industry produces?”
What about the ordinary everyday effects of these machines upon you and me as an individual? We can see that the new machinery will apply on a small scale even to us. Small machines using a few electronic tubes—much like a radio set, for example—and containing spools of magnetic wire or magnetic tape will doubtless be available to us. We shall be able to use them to keep addresses and telephone numbers, to figure out the income tax we should pay, to help us keep accounts and make ends meet, to remember many things we need to know, and perhaps even to give us more information. For there are a great many things that all of us could do much better if we could only apply what the wisest of us knows.
[Pg 195] We can even imagine what new machinery for handling information may some day become: a small pocket instrument that we carry around with us, talking to it whenever we need to, and either storing information in it or receiving information from it. Thus the brain with a motor will guide and advise the man just as the armor with a motor carries and protects him.
[Pg 196]
It is often easier for men to create a device than to guide it well afterwards: it is often easier for a scientist to study his science than to study the results for good or evil that his discoveries may lead to. But it is not right nor proper for a scientist, a man who is loyal to truth as an ideal, to have no regard for what his discoveries may lead to.
This principle is now being widely recognized. Many scientists today—both as individuals and as groups, and especially the atomic scientists—are considering the results of their scientific discoveries; and they are sharing in the effort to render those results truly useful to humanity.
It would be easy to leave out of this book any discussion of how machines that think may be controlled, any consideration of how they may be made truly useful to humanity. But that would be hardly right or proper. In concluding a book such as this one, that touches on many aspects of machines that think, we need to consider what can and should be done to make such machines of true benefit to all of humanity.
So, we come to the most important of all our questions: What sort of control over machines that think do we need in human society?
From a narrow point of view, a machine that only thinks produces only [Pg 197] information. It takes in information in one state, and it puts out information in another state. From this viewpoint, information in itself is harmless; it is just an arrangement of marks; and accordingly, a machine that thinks is harmless, and no control is necessary.
Although it is true that the information produced only becomes good or evil after other machinery or human beings act on the information, in reality a machine with the power to produce information is constructed only for the reason of its use. We want to know what such machines can tell us only because we can then proceed to act much more efficiently than before. For example, a guided missile needs a mechanical brain only because then it can reach its target. In all cases mechanical brains are inseparable from their uses.
For the purposes of this chapter, the narrow view will be rejected because it dodges the issue. We shall be much concerned with the combination of a machine that thinks with another machine that acts; and we shall often call this combination the robot machine.
Now, before launching further into the discussion, we need to say that the conclusions suggested in this chapter are not final. Even if they are expressed a little positively in places, they are nevertheless subject to change as more information is discovered and as the appraisal of information changes with time. Also, almost any conclusions about social control—including, certainly, the conclusions in this chapter—are subject to controversy. But controversy is good: it leads to thought. The more minds that go to work on solving the problem of social control over robot machines and other products of the new technology—which is rushing upon us from the discoveries of the scientists—the better off we all will be. If, while stimulating disagreement, the ideas expressed in this chapter should succeed in stimulating thought and deliberation, the purpose of this chapter will be well fulfilled.
Up to this point in this book, the emphasis has been on possibilities of benefits to humanity that may arise from machines that think. In this chapter, devoted as it is to the subject of control, the emphasis [Pg 198] is on possibilities for harm. Both possibilities are valid, and the happening of either depends upon the actions of men. In much the same way, atomic energy is a great possibility for benefit and for harm. It is the nature of control to put a fence around danger; and so it is natural in this chapter that the weight of attention should shift to the dangerous aspects of machines that think.
Perhaps a reader may feel that a chapter of this kind is rather out of place in a book, such as this one, that seeks to be scientific. If so, he is reminded that, in accordance with the general suggestions for reading this book stated in the preface, he should omit this chapter.
Perhaps the first study of the consequences of a machine that thinks is a prophetic novel called Frankenstein, written more than a hundred years ago, in 1818. The author, then only 21 years old, was Mary W. Godwin, who became the wife of the poet Percy Bysshe Shelley.
According to the story, a young Swiss, an ardent student of physiology and chemistry, Victor Frankenstein, finds the secret of life. He makes an extremely ugly, clever, and powerful monster, with human desires. Frankenstein promptly flees from his laboratory and handiwork. The monster, after seeking under great hardships for a year or two to earn fair treatment among men, finds himself continually attacked and harmed on account of his ugliness, and he becomes embittered. He begins to search for his creator for either revenge or a bargain. When they meet:
“I expected this reception,” said the daemon.
“All men hate the wretched; how then must I be hated who am miserable beyond all living things! Yet you my creator detest and spurn me, thy creature, to whom thou art bound by ties only dissoluble by the annihilation of one of us. You purpose to kill me. How dare you sport thus with life? Do your duty towards me, and I will do mine towards you and the rest of mankind. If you will comply with my conditions, I will leave them and you at peace; but if you refuse, I will glut the maw of death, until it be satiated with the blood of your remaining friends.”
Frankenstein starts to comply with the main condition, which is to make [Pg 199] a mate for the monster; but Frankenstein cannot bring himself to do it. So the monster causes the death one after another of all Frankenstein’s family and closest friends; and the tale finally ends with the death of Frankenstein and the disappearance of the monster.
As the dictionary says about Frankenstein, “The name has become a synonym for one destroyed by his own works.”
Perhaps the next study of the consequences of a machine that thinks is a remarkable play called R.U.R. (for Rossum’s Universal Robots), first produced in Prague in 1921. Karel Čapek, the Czech dramatist who wrote it, was then only 31. The word “robot” comes from the Czech word “robota,” meaning compulsory service.
According to the play, Rossum the elder, a scientist, discovered a “method of organizing living matter” that was “more simple, flexible, and rapid” than the method used by nature. Rossum the younger, an engineer, founded a factory for the mass production of artificial workmen, robots. They had the form of human beings, intelligence, memory, and strength; but they were without feelings.
In the first act, the factory under Harry Domin, General Manager, is busy supplying robots to purchasers all over the world—for work, for fighting, for any purpose at all, to anyone who could pay for them. Domin declares:
“... in ten years, Rossum’s Universal Robots will produce so much corn, so much cloth, so much everything that things will be practically without price. There will be no poverty. All work will be done by living machines. Everybody will be free from worry and liberated from the degradation of labor. Everybody will live only to perfect himself.... It’s bound to happen.”
In the second act, ten years later, it turns out that Domin and the others in charge of the factory have been making some robots with additional human characteristics, such as the capacity to feel pain. The newer types of robots, however, have united all the robots against man, for the robots declare that they are “more highly developed than man, stronger, and more intelligent, and man is their parasite.” [Pg 200]
In the last act, the robots conquer and slay all men except one—an architect, Alquist, who in the epilogue provides a final quirk to the plot.
Now what is fact and what is fancy in these two warnings given to us a hundred years apart?
Of course, it is very doubtful that a Frankenstein monster or a Rossum robot will soon be constructed with nerves, flesh, and blood like an animal body. But we know that many types of robot machines can even now be constructed out of hardware—wheels, motors, wires, electronic tubes, etc. They can handle many kinds of information and are able to perform many kinds of actions, and they are stronger and swifter than man.
Of course, it is doubtful that the robot machines, by themselves and of their own “free will,” will be dangerous to human beings. But as soon as antisocial human beings have access to the controls over robot machines, the danger to society becomes great. We want to escape that danger.
A natural longing of many of us is to escape to an earlier, simpler life on this earth. Victor Frankenstein longed to undo the past. He said:
“Learn from me, if not by my precepts, at least by my example, how dangerous is the acquirement of knowledge, and how much happier that man is who believes his native town to be the world, than he who aspires to become greater than his nature will allow.”
Any sort of return to the past is, of course, impossible. It is doubtful that men could, even if they wanted to, stop the great flood of technical knowledge that science is now producing. We all must now face the fact that the kind of world we used to live in, even so recently as 1939, is gone. There now exist weapons and machines so powerful and dangerous in the wrong hands that in a day or two most of the people of the earth could be put to death. Giant brains are closely related to at least two of these weapons: scientists have already used mechanical brains for solving problems about atomic explosives and [Pg 201] guided missiles. In addition, thinking mechanisms designed for the automatic control of gunfire were an important part of the winning of World War II. They will be a still more important part of the fighting of any future war.
Nor can we escape to another part of the earth which the new weapons will not reach. At 300 miles an hour, any spot on earth can be reached from any other in less than 48 hours. A modern plane exceeds this speed; a rocket or guided missile doubles or trebles it.
Nor can we trust that some kind of good luck will pull us through and help men to escape the consequences of what men do. Both Frankenstein and Domin reaped in full the consequences of what they did. The history of life on this earth that is recorded in the rocks is full of evidence of races of living things that have populated the earth for a time and then become extinct, such as the dinosaurs. In that long history, rarely does a race survive. In our own day, insects and fungi rather than men have shown fitness to survive and spread over the earth: witness the blight that destroyed the chestnut trees of North America, in spite of the best efforts of scientists to stop it.
There seems to be no kind of escape possible. It is necessary to grapple with the problem: How can we be safe against the threat of physical harm from robot machines?
The other chief threat from robot machines is against our economic life. Harry Domin, in R.U.R., you remember, prophesied: “All work will be done by living machines.” As an example, in the magazine Modern Industry for Feb. 15, 1947, appeared a picture of a machine for selling books, and under the picture were the words:
Another new product in robot salesmen—Latest in the parade of mechanical vending machines is this book salesman.... It is designed for use in hospitals, rail terminals, and stores. It offers 15 different titles, selected manually, and obtained by dropping quarter in slot. Cabinet stores 96 books.
Can you feel the breath of the robot salesman, workman, engineer,——, on the back of your neck? [Pg 202]
At the moment when we combine automatic producing machinery and automatic controlling machinery, we get a vast saving in labor and a great increase in technological unemployment. In extreme cases, perhaps, the effect of robot machines will be the disappearance of men from a factory. Such a factory will be like a modern power plant that turns a waterfall into electricity: once the machinery is installed, only one watchman is ordinarily needed. But, in most cases, this will be the effect: in a great number of factories, mines, farms, etc., the labor force needed will be cut by a great proportion. The effect is not different in quality, because the new development is robot machinery; but the amount of technological unemployment coming from robot machines is likely to be considerably greater than previously.
The robot machine raises the two questions that hang like swords over a great many of us these days. The first one is for any employee: What shall I do when a robot machine renders worthless all the skill I have spent years in developing? The second question is for any businessman: How shall I sell what I make if half the people to whom I sell lose their jobs to robot machines?
The two chief harmful effects upon humanity which are to be expected from robot machines are physical danger and unemployment. These are serious risks, and some degree of social control is needed to guard against them.
There will also be very great advantages from robot machines. The monster in Frankenstein is right when he says, “Do your duty towards me, and I will do mine towards you and the rest of mankind.” And Harry Domin in R.U.R. is right as to possibility when he says, “There will be no poverty.... Everybody will be free from worry.” Social control must also be concerned with how the advantages from robot machines are to be shared.
The problem of social control over men and their devices has always had two sides. The first side deals with what we might plan for control if men were reasonable and tolerant. This part of the problem seems [Pg 203] relatively easy. The other side deals with what we must ordinarily arrange, since most men are often unreasonable and prejudiced and, as a result, often act in antisocial ways. This part of the problem is hard. Let us begin with the easier side first.
In seeking to fulfill wants and achieve safety, men have used hundreds of types of control. The main types are usually called political and economic systems, but there are always great quantities of exceptions. The more mature and freer the society, the greater the variety of types of control that can be found in it.
Probably the most widely used type of control in this country is private and public control working together, as private ownership and public regulation—for example, railroads, banks, airlines, life insurance companies, telephone systems, and many others. It would be reasonable to expect private ownership and public regulation of a great many classes of robot machines, to the end that they would never threaten the safety of people.
Another common type of control is public ownership and operation; examples are toll bridges, airports, city transit systems, and water-supply systems. Atomic energy was so clearly fraught with serious implications that in 1946 the Congress of the United States placed it entirely under public control expressed as the Atomic Energy Commission. There is a class of robot machinery which has already reached the stage of acute public concern: guided missiles and automatic fire-control. It would be reasonable that in this country all activity in this subdivision should be under close control by the Department of Defense.
In the international arena, again, the problem becomes soluble if we assume men to be reasonable. An international agency, such as an organ of the United Nations, would take over inspection and control of robot machine activities closely affecting the public safety anywhere in the world. Particularly, this agency would concern itself with guided missiles, robot pilots for planes, automatic gunfire control, etc. Much manufacturing skill is needed to make such products as these: the factories where they could be manufactured would thereby be [Pg 204] determined. Also, a giant brain is a useful device for solving scientific problems about weapons of mass destruction. So the agency would need to inspect the problems being solved on such machines. This agency would be responsible to a legislature or an executive body representing all the people in the world—if men were reasonable.
In regard to the effects of robot machines on unemployment, again, if men were reasonable, the problem would be soluble. The problem is equivalent to the problem of abundance: how should men distribute the advantages of a vast increase in production among all the members of society in a fair and sensible way? A vast increase in production is not so impossible as it may seem. For example, in 1939, with 45 million employed, the United States index of industrial production was at 109, and, in 1943, with 52½ million employed, the index of production was at 239.
If men were reasonable, the net profits from robot machinery would be divided among (1) those who had most to do with devising the new machinery, and (2) all of society. A rule would be adopted (probably it could be less complicated than some existing tax rules) which would take into account various factors such as rewards to the inventors, incentives to continue inventing, adequate assistance to those made unemployed by the robot machines, reduction of prices to benefit consumers, and contributions to basic and applied scientific research.
In fact, under the assumption “if men were reasonable,” it would hardly be necessary to devote a chapter to the problem of social control over robot machines!
The discussion above of how robot machines could be controlled supposing that men were reasonable, seems, of course, to be glaringly impractical. Men are not reasonable on most occasions most of the time. If we stopped at this point, again we would be dodging the issue. What are the obstacles to reasonable control?
There are, it seems, two big obstacles and one smaller one to reasonable types of social control over robot machines. The smaller one [Pg 205] is ignorance, and the two big obstacles are prejudice and a narrow point of view.
By ignorance we mean lack of knowledge and information. Now mechanical brains are a new and intricate subject. A great many people will, through no fault of their own, naturally remain uninformed about mechanical brains and robot machines for a long time. However, there is a widespread thirst for knowledge these days: witness in magazines, for example, the growth of the article and the decline of the essay. There is also a fairly steady surge of knowledge from the austere scientific fountain of new technology. We can thus see both a demand and a supply for information in such fields as mechanical brains and robot machines. We can expect, therefore, a fairly steady decline in ignorance.
Prejudice is a much more serious obstacle to reasonable control over robot machines. It will be worth our while to examine it at length.
Prejudice is frequent in human affairs. For example, in some countries, but not in all, there is conflict among men, based on their religious differences. Again, in other countries, but not in all, there is wide discrimination among men, based on the color of their skin. Over the whole world today, there is a sharp lack of understanding between conservatives, grading over to reactionaries, on the one hand, and liberals, grading over to radicals, on the other hand. All these differences are based on men’s attitudes, on strongly held sets of beliefs. These attitudes are not affected by “information”; the “information” is not believed. The attitudes are not subject to “judgment”; they come “before judgment”: they are prejudices. Even in the midst of all the science of today, prejudice is widespread. In Germany, from 1933 to 1939, we saw one of the most scientific of countries become one of the most prejudiced.
Prejudice is often difficult to detect. We find it hard to recognize even in ourselves. For a prejudice always seems, to the person who has [Pg 206] it, the most natural attitude in the world. As we listen to other people, we are often uncertain how to separate information, guesses, humor, prejudice, etc. Circumstances compel us to accept provisionally quantities of statements just on other people’s say-so. A good test of a statement for prejudice, however, is to compare it with the scientific view.
Prejudice is most dangerous for society. Its more extreme manifestations are aggressive war, intolerance (especially of strange people and customs), violence, race hatred, etc. In the consuming hatred that a prejudiced man has towards the object of his prejudice, he is likely to destroy himself and destroy many more people besides. In former days, the handy weapon was a sword or a pistol; not too much damage could be done when one man ran amuck. But nowadays a single use of a single weapon has slain 70,000 people (the atom bomb dropped at Hiroshima), and so a great many people live anxious and afraid.
What is prejudice? How does it arise? How can it be cured, and thus removed from obstructing reasonable control over robot machines and the rest of today’s amazing scientific developments?
Prejudice is a disease of men’s minds. It is infectious. The cause and development of the disease are about as follows: Deprive someone of something he deeply needs, such as affection, food, or opportunity. In this way hurt him, make him resentful, hostile; but prevent him from expressing his resentments in a reasonable way, giving him instead false outlets, such as other people to hurt, myths to believe, hostile behavior patterns to imitate. He will then break out with prejudices as if they were measles. The process of curing the disease of prejudice is about as follows: Make friends with the patient; win his trust. Encourage him to pour out his half-forgotten hates. Help him to talk them over freely, by means of questions but not criticisms, until finally the patient achieves insight, sees through his former prejudices, and drops them.
In these days prejudice is a cardinal problem of society. It is perhaps conservative to say that a chief present requirement for the survival of human society—with the atom bomb, bacterial warfare, guided missiles, etc., near at hand—is cure of prejudice and its consequences, irrational and unrestrained hate. [Pg 207]
A narrow point of view regarding what is desirable or good is the third obstacle to rational control over robot machines. What do we mean by this?
Our point of view as a two-year-old is based on pure self-interest. If we see a toy, we grab it. There is no prejudice about this; it is entirely natural—for two-year-olds. As we grow older, our point of view concerning what is good or desirable rapidly broadens: we think of others and their advantage besides our own. For example, we may become interested in a conservation program to conserve birds, or soil, or forests, and our point of view expands, embraces these objectives, which become part of our personality and loyalties.
Unfortunately, it seems to be true that the expanding point of view, the expanding loyalties, of most people as they grow up are arrested somewhere along the line of: self, family, neighborhood, community, section of country, nation. An honorable exception is the scientists’ old and fine tradition of world-wide unity and loyalty in the search for objective truth.
Now the problem of rational control over robot machines and other parts of the new technology is no respecter of national boundaries. To be solved it requires a world-wide point of view, a loyalty to human society and its best interests, a social point of view.
Almost all that you and I have and do and think is the result of a long history of human society on this earth. All men on the earth today are descendants of other men who lived 1000, 2000, 3000 ... years ago, whether they were Romans or Chinese or Babylonians or Mayas or members of any other race. To ride in a subway or an airplane, to talk on the telephone, to speak a language, to calculate, to survive smallpox or the black death, etc.—all these privileges are our inheritance from countless thousands of other human beings, of many countries, and nearly all of whom are now dead. During our lives we pass on to our own children an inheritance in which our own contribution is remarkably small. Since each person is the child of two others, the number of our forefathers is huge, and we are all undoubtedly blood cousins. Because [Pg 208] of this relationship, and because we owe to the rest of society nearly all that we are, we have a social responsibility—we need to hold a social point of view. Each of us needs to accept and welcome a world-wide social responsibility, as a member of human society, as a beneficiary and trustee of our human inheritance. Otherwise we are drones, part of the hive without earning our keep. The social point of view is equitable, it is inspiring, and it is probably required now in order for human beings to survive. We need to let go of a narrow point of view.
We have now outlined the problem of social control over robot machines, supposing that human beings were reasonable. We have also discussed the practical obstacles that obstruct reasonable control.
It is not easy to think of any yet organized group of people anywhere that would have both the strength and the vision needed to solve this problem through its own efforts. For example, a part of the United Nations might have some of the vision needed, but it does not have the power. Consequently, it is necessary and desirable for individuals and groups everywhere to take upon themselves an added load of social responsibility—just as they tend to do in time of war. People often “want to do their share.” Through encouragement and education, the basic attitude of a number of people can contain more of “This is our business; we have a responsibility for helping to solve this problem.” We also need public responsibility; we need a public body responsible for study, education, advice, and some measure of control. It might be something like an Atomic Energy Commission, Bacterial Defense Commission, Mental Health Commission, and Robot Machine Commission, all rolled into one.
When, at last, there is an effective guarantee of the two elements physical safety and adequate employment, then at last we shall all be free from the threat of the robot machine. We can then welcome the robot machine as our deliverer from the long hard chores of many centuries.
[Pg 209]
The purpose of this book is to explain machines that think, without using technical words any more than necessary. This supplement is a digression. Its purposes are to consider how to explain in this way and to discuss the attempt made in this book to achieve simple explanation.
Words are the chief instruments we use for explaining. Of course, many other devices—pictures, numbers, charts, models, etc.—are also used; but words are the prime tools. We do most of our explaining with them.
Words, however, are not very good instruments. Like a stone arrow-head, a word is a clumsy weapon. In the first place, words mean different things on different occasions. The word “line,” for example, has more than fifty meanings listed in a big dictionary. How do we handle the puzzle of many meanings? As we grow older we gather experience and we develop a truly marvelous capacity to listen to a sentence and then fit the words together into a pattern that makes sense. Sometimes we notice the time lag while our brain hunts for the meaning of a word we have heard but not grasped. Then suddenly we guess the needed meaning, whereupon we grasp the meaning of the sentence as a whole in much the same way as the parts of a puzzle click into place when solved.
Another trouble with words is that often there is no good way to tell someone what a word means. Of course, if the word denotes a physical object, we can show several examples of the object and utter the word each time. In fact, several good illustrations of a word denoting a physical thing often tell most of its meaning. But the rest of its meaning we often do not learn for years, if ever. For instance, two people would more likely disagree than agree about what should be [Pg 210] called a “rock” and what should be called a “stone,” if we showed them two dozen examples.
In the case of words not denoting physical objects, like “and,” “heat,” “responsibility,” we are worse off. We cannot show something and say, “That is a ···.” The usual dictionary is of some help, but it has a tendency to tell us what some word A means by using another word B, and when we look up the other word B we find the word A given as its meaning. Mainly, however, to determine the meanings of words, we gather experience: we soak up words in our brains and slowly establish their meanings. We seem to use an unconscious reasoning process: we notice how words are used together in patterns, and we conclude what they must mean. Clearly, then, words being clumsy instruments, the more experience we have had with a word, the more likely we are to be able to use it, work with it, and understand it. Therefore explanation should be based chiefly on words with which we have had the most experience. What words are these? They will be the well-known words. A great many of them will be short.
Now what is the set of all the words needed to explain simply a technical subject like machines that think? For we shall need more words than just the well-known and short ones. This question doubtless has many answers; but the answer used in this book was based on the following reasoning. In a book devoted to explanation, there will be a group of words (1) that are supposed to be known already or to be learned while reading, and (2) that are used as building blocks in later explanation and definitions. Suppose that we call these words the words for explaining. There are at least three groups of such words:
Group 1. Words not specially defined that are so familiar that every reader will know all of them; for example, “is,” “much,” “tell.”
Group 2. Words not specially defined that are familiar, but perhaps some reader may not know some of them; for example, “alternative,” “continuous,” “indicator.”
Group 3. Words that are not familiar, that many readers are not expected to know, and that are specially defined and explained in the body of the book; for example, “abacus,” “trajectory,” “torque.”
In writing this book, it was not hard to keep track of the words in the third group. These words are now listed in the index, together with the [Pg 211] page where they are defined or explained. (The index, of course, also lists phrases that are specially defined.)
But what division should be made between the other two groups? A practical, easy, and conservative way to separate most words between the first and second groups seemed to be on the basis of number of syllables. All words of one syllable—if not specially defined—were put in Group 1. Also, if a word became two syllables only because of the addition of one of the endings “-es,” “-ed,” “-ing,” it was kept in Group 1, for these endings probably do not make a word any harder to understand. In addition, there were put into Group 1:
Of course, not all these words would be familiar to every reader (for example, “Maya”), but in the way they occur, they are usually not puzzling, for we can tell from the context just about what they must mean.
All remaining words for explaining—chiefly, words of two or more syllables and not specially defined—were put in Group 2 and were listed during the writing of this book. Many Group 2 words, of course, would be entirely familiar to every reader; but the list had several virtues. No hard words would suddenly be sprung like a trap. The same word would be used for the same idea. Every word of two or more syllables was continually checked: is it needed? can it be replaced by a shorter word? It is perhaps remarkable that there were fewer than 1800 different words allowed to stay in this list. This fact should be a comfort to a reader, as it was to the author.
Now there are more words in this book than words for explaining. So we shall do well to recognize:
Group 4. Words that do not need to be known or learned and that are not used in later explanation and definitions.
These words occur in the book in such a way that understanding them, though helpful, is not essential. One subdivision of Group 4 are names that appear just once in the book, as a kind of side remark, for example, “a chemical, called acetylcholine.” Such a name will also appear in the index, but it is not a word for explaining. Another subdivision of Group 4 are words occurring only in quotations. For example, in the quotation from Frankenstein [Pg 212] on page 198, a dozen words appear that occur nowhere else in the book, including “daemon,” “dissoluble,” “maw,” “satiate.” Clearly we would destroy the entire flavor of the quotation if we changed any of these words in any way. But only the general drift of the quotation is needed for understanding the book, and so these words are Group 4 words.
In this way the effort to achieve simple explanation in this book proceeded. But even supposing that we could reach the best set of words for explaining, there is more to be done. How do we go from simple explanation to understanding?
Understanding an idea is basically a standard process. First, we find the name of the idea, a word or phrase that identifies it. Then, we collect true statements about the idea. Finally, we practice using them. The more true statements we have gathered, and the more practice we have had in applying them, the more we understand the idea.
For example, do you understand zero? Here are some true statements about zero.
1. Zero is a number.
2. It is the number that counts none or nothing.
3. It is marked 0 in our usual numeral writing.
4. The ancient Romans, however, had no numeral for it. Apparently, they did not think of zero as a number.
5. 0 is what you get when you take away 17 from 17, or when you subtract any number from itself.
6. If you add 0 to 23, you get 23; and if you add 0 to any number, you get that number unchanged.
7. If you subtract 0 from 48, you get 48; and if you subtract 0 from any number, you get that number unchanged.
8. If you multiply 0 by 71, you get 0; and if you multiply together 0 and any number, you get 0.
9. Usually you are not allowed to divide by 0: that is against the rules of arithmetic.
10. But if you do, and if you divide 12 by 0, for example—and there are times when this is not wrong—the result is called infinity and is marked ∞, a sign that is like an 8 on its side.
This is not all the story of zero; it is one of the most important of numbers. But, if you know these statements about zero, and have had some practice in applying them, you have a good [Pg 213] understanding of zero. Incidentally, a mechanical brain knows all these statements about zero and a few more; they must be built into it.
For us to understand any idea, then, we pursue three aims:
We can do this about any idea. Therefore, we can understand any idea, and the degree of our understanding increases as the number of true statements mastered increases.
Perhaps this seems to be a rash claim. Of course, it may take a good deal of time to collect true statements about many ideas. In fact, a scientist may spend thirty years of his life trying to find out from experiment the truth or falsehood of one statement, though, when he has succeeded, the fact can be swiftly told to others. Also, we all vary in the speed, perseverance, skill, etc., with which we can collect true statements and apply them. Besides, some of us have not been taught well and have little faith in our ability to carry out this process: this is the greatest obstacle of all. But, there is in reality no idea in the field of existing science and knowledge which you or I cannot understand. The road to understanding lies clear before us.
[Pg 214]
In the course of our discussion of machines that think, we have had to refer without much explanation to a number of mathematical ideas. The purpose of this supplement is to explain a few of these ideas a little more carefully than seemed easy to do in the text and, at the end of the supplement, to put down briefly some additional notes for reference.
Suppose that we have to multiply 372 by 465. With the ordinary school method, we write 465 under the 372 and proceed about as follows: 5 times 2 is 10, put down the 0 and carry the 1; 5 times 7 is 35, 35 and 1 is 36, put down the 6 and carry the 3; 5 times 3 is 15, 15 and 3 is 18, put down the 8 and carry the 1; ... The method is based mainly on a well-learned subroutine of continually changing steps:
We can, however, simplify this subroutine for a machine by delaying the carrying. We collect in one place all the right-hand digits of partial products, collect in another place all the left-hand digits, and delay all addition until the end.
For example, let us multiply 372 by 465 with this method: [Pg 215]
| Right-Hand Digits |
Left-Hand Digits |
Usual Method for Comparison |
|---|---|---|
| 372 | 372 | 372 |
| × 465 | × 465 | × 465 |
| 550 | 131 | 1860 |
| 822 | 141 | 2232 |
| 288 | 120 | 1488 |
| 37570 | 13541 | 172980 |
Final Addition |
||
| 37570 | ||
| + 13541 | ||
| 172980 | ||
37570 is called the right-hand component of the product. It is convenient to fill in with 0 the space at the end of 13541 and to call 135410 the left-hand component of the product.
This process is called multiplying by right- and left-hand components. It has the great advantage that no carrying is necessary to complete any line of the original multiplications. Some computing machines use this process. Built into the hardware of the machine is a multiplication table up to 9 × 9. The machine, therefore, can find automatically the right-hand digit and the left-hand digit of any partial product. In a computing machine that uses this process, all the left-hand digits are automatically added in one register, and all the right-hand digits are added in another register. The only carrying that is needed is the carrying as the right-hand digits are accumulated and as the left-hand digits are accumulated. At the end of the multiplication, one of the registers is automatically added into the other, giving the product.
Another device used in computing machines for multiplying is to change the multiplier into a set of digits 0 to 5 that are either positive or negative. For example, suppose that we want to multiply 897 by 182. We note that 182 equals 200 minus 20 plus 2, and so we can write it as
The minus over the 2 marks it as a negative digit 2. Then to multiply we have:
The middle 1794 is subtracted. This process is usually called short-cut multiplication. Everybody discovers this trick when he decides that multiplying by 99 is too much work, that it is easier to multiply by 100 and subtract once. [Pg 216]
We are well accustomed to decimal notation in which we use 10 decimal digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and write them in combinations to designate decimal numbers. In binary notation we use two binary digits 0, 1 and write them in combinations to designate binary numbers. For example, the first 17 numbers, from 0 to 16 in the decimal notation, correspond with the following numbers in binary notation:
| Decimal | Binary | Decimal | Binary |
|---|---|---|---|
| 0 | 0 | ||
| 1 | 1 | 9 | 1001 |
| 2 | 10 | 10 | 1010 |
| 3 | 11 | 11 | 1011 |
| 4 | 100 | 12 | 1100 |
| 5 | 101 | 13 | 1101 |
| 6 | 110 | 14 | 1110 |
| 7 | 111 | 15 | 1111 |
| 8 | 1000 | 16 | 10000 |
In decimal notation, 101 means one times a hundred, no tens, and one. In binary notation, 101 means one times four, no twos, and one. The successive digits in a decimal number from right to left count 1, 10, 100, 1000, 10000, ...—successive powers of 10 (for this term, see the end of this supplement). The successive digits in a binary number from right to left count 1, 2, 4, 8, 16, ...—powers of 2.
The decimal notation is convenient when equipment for computing has ten positions, like the fingers of a man, or the positions of a counter wheel. The binary notation is convenient when equipment for computing has just two positions, like “yes” or “no,” or current flowing or no current flowing.
Addition, subtraction, multiplication, and division can all be carried out unusually simply in binary notation. The addition table is simple and consists only of four entries.
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 |
The multiplication table is also simple and contains only four entries. [Pg 217]
| × | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Suppose that we add in binary notation 101 and 1001:
| Binary Addition |
Check |
|---|---|
| 101 | 5 |
| + 1001 | 9 |
| 1110 | 14 |
We proceed: 1 and 1 is 10; write down 0 and carry 1; 0 and 0 is 0, and 1 to carry is 1; and 1 and 0 is 1; and then we just copy the last 1. To check this we can convert to decimal and see that 101 is 5, 1001 is 9, and 1110 is 14, and we can verify that 5 and 9 is 14.
One of the easiest ways to subtract in binary notation is to add a ones complement (that is, the analogue of the nines complement) and use end-around-carry (for these two terms, see the end of this supplement). A ones complement can be written down at sight by just putting 1 for 0 and 0 for 1. For example, suppose that we subtract 101 from 1110:
| Direct Subtraction |
Check | Subtraction by Adding Ones Complement |
|---|---|---|
| 1110 | 14 | 1110 |
| - 101 | - 5 | + 1010 |
| 1001 | 9 | (1)1000 |
| ↓ | ||
| ⎯→ 1 | ||
| 1001 |
Multiplication in the binary notation is simple. It amounts to (1) adding if the multiplier digit is 1 and not adding if the multiplier digit is 0, and (2) moving over or shifting. For example, let us multiply 111 by 101:
| Binary Multiplication |
Check |
|---|---|
| 111 | 7 |
| × 101 | × 5 |
| 111 | |
| 111 | |
| 100011 | 35 |
[Pg 218] The digit 1 in the 6th (or nth) binary place from the right in 100011 stands for 1 times 2 to the 5th (or n-1 th) power, 2 × 2 × 2 × 2 × 2 = 32. The result 100011 is translated into 32 plus 2 plus 1, which equals 35 and verifies.
Division in the binary notation is also simple. It amounts to (1) subtracting (yielding a quotient digit 1) or not subtracting (yielding a quotient digit 0), and (2) shifting. We never need to try multiples of the divisor to find the largest that can be subtracted yet leave a positive remainder. For example, let us divide 1010 (10 in decimal) into 10001110 (142 in decimal):
In decimal notation, digits to the right of the decimal point count powers of ⅒. In binary notation, digits to the right of the binary point count powers of ½: ½, ¼, ⅛, ¹/₁₆.... For example, 0.1011 equals ½ + ⅛ + ¹/₁₆, or ¹¹/₁₆.
If we were accustomed to using binary numbers, all our arithmetic would be very simple. Furthermore, binary numbers are in many ways much better for calculating machinery than any other numbers. The main problem is converting numbers from decimal notation to binary. One method depends on storing the powers of 2 in decimal notation. The rule is: subtract successively smaller powers of 2; start with the largest that can be subtracted, and count 1 for each power that goes and 0 for each power that does not. For example, 86 in decimal becomes 1010110 in binary:
| 86 | ||
| 64 | 64 goes | 1 |
| 22 | 32 does not go | 0 |
| 16 | 16 goes | 1 |
| 6 | 8 does not go | 0 |
| 4 | 4 goes | 1 |
| 2 | 2 goes | 1 |
| 2 | 1 does not go | 0 |
| 0 |
[Pg 219] It is a little troublesome to remember long series of 1’s and 0’s; in fact, to write any number in binary notation takes about 3⅓ times as much space as decimal notation. For this reason we can separate binary numbers into triples beginning at the right and label each triple as follows:
| Triple | Label |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
For example, 1010110 would become 1 010 110 or 126. This notation is often called octal notation, because it is notation in the scale of eight.
Another kind of notation for numbers is biquinary notation, so called because it uses both 2’s and 5’s. Essentially this notation is very like Roman numerals, ancient style. By ancient style we mean, for example, VIIII instead of IX. In the following table we show the first two dozen numbers in decimal, biquinary, and ancient Roman notation:
| Decimal | Biquinary | Roman |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | I |
| 2 | 2 | II |
| 3 | 3 | III |
| 4 | 4 | IIII |
| 5 | 10 | V |
| 6 | 11 | VI |
| 7 | 12 | VII |
| 8 | 13 | VIII |
| 9 | 14 | VIIII |
| 10 | 100 | X |
| 11 | 101 | XI |
| 12 | 102 | XII |
| 13 | 103 | XIII |
| 14 | 104 | XIIII |
| 15 | 110 | XV |
| 16 | 111 | XVI |
| 17 | 112 | XVII |
| 18 | 113 | XVIII |
| 19 | 114 | XVIIII |
| 20 | 200 | XX |
| 21 | 201 | XXI |
| 22 | 202 | XXII |
| 23 | 203 | XXIII |
The biquinary columns alternate in going from 0 to 4 and from 0 to 1. The digits from 0 to 4 are not changed. The digits from 5 to 9 are changed into 10 to 14. We see that the biquinary digits are 0 to 4 in odd columns and 0, 1 in even columns, counting from the right.
This is the notation actually expressed by the abacus. The beads of the abacus show by their positions groups of 2 and 5 (see Fig. 1). [Pg 220]
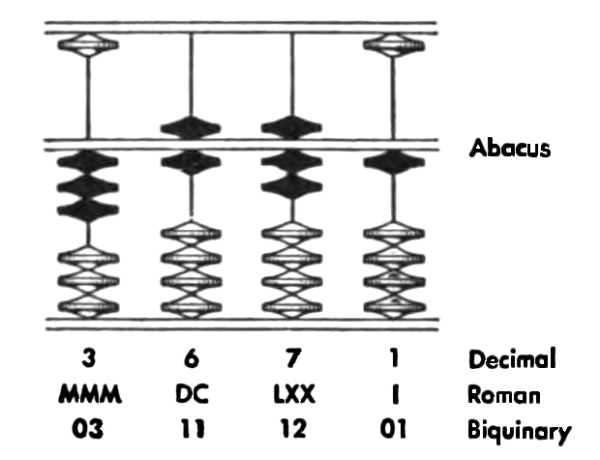
Fig. 1. Abacus and notations.
One of the operations of algebra that is important for a mechanical brain is approximation, the problem of getting close to the right value of a number. Take, for example, finding square root (see the end of this supplement). The ordinary process taught in school is rather troublesome. We can set down another process, however, using a desk calculator to do division, which gives us square root with great speed.
Suppose that we want to find the square root of a number N, and suppose that we have x₀ as a guessed square root correct to one figure. For example, N might be 67.2 and x₀ might be 8, chosen because 8 × 8 is 64, and 9 × 9 is 81, and it seems as if 8 should be near the square root of 67.2. Here is the process:
Now repeat:
Every time this process is repeated, the new x comes a great deal closer to the correct square root. In fact it can be shown that, if x₀ is correct to one figure, then:
| Approximation | Is Correct To ··· Figures |
|---|---|
| x₁ | 2 |
| x₂ | 4 |
| x₃ | 8 |
| x₄ | 16 |
Let us see how this actually works out with 67.2 and a 10-column desk calculator. [Pg 221]
Round 1: 8 divided into 67.2 gives 8.4. One half of 8 plus 8.4 is 8.2. This is x₁.
Round 2: 8.2 divided into 67.2 gives 8.195122. One half of 8.2 plus 8.195122 is 8.197561. This is x₂.
Round 3: 8.197561 divided into 67.2 gives 8.197560225. One half of 8.197561 and 8.197560225 is 8.1975606125. This is x₃.
Checking x₃, we find that 8.1975606125 divided into 67.2 gives 8.1975606126 approximately.
In this case, then, x₃ is correct to more than 10 figures. In other words, with a reasonable guess and two or three divisions we can obtain all the accuracy we can ordinarily use. This process is called rapid approximation, or rapidly convergent approximation, since it converges (points or comes together) very quickly to the number we are seeking.
Another important operation of algebra is interpolation, the problem of putting values smoothly in between other values. For example, suppose that we have the table:
| x | y |
|---|---|
| 5 | 26 |
| 6 | 37 |
| 7 | 50 |
| 8 | 65 |
| 9 | 82 |
Suppose that we want to find the value that y (or yₓ) ought to have when x has the value of 7.2. This is the problem of interpolating y so as to find y at the value of 7.2, y₇ˌ₂.
One way of doing this is to discover the formula that expresses y and then to put x into that formula. This is not always easy. Another way is to take the difference between y₇ and y₈, 15, and share the difference appropriately over the distance 7 to 7.2 and 7.2 to 8. We can, for example, take ²/₁₀ of 15 = 3, add that to y₇ = 50, and obtain an estimated y₇ˌ₂ = 53. This is called linear interpolation, since the difference 0.2 in the value of x is used only to the first power. It is a good practical way to carry out most interpolation quickly and approximately.
Actually here y = x² + 1, and so the true value of y₇ˌ₂ is (7.2 × 7.2) + 1, or 52.84, which is rather close to 53. Types of interpolation procedures more accurate than linear interpolation will come much nearer still to the true value.
We turn now to the algebra of logic. The first half of Chapter 9, “Reasoning” (through the section “Logical-Truth Calculation by [Pg 222] Algebra”), introduces this subject. There the terms truth values, truth tables, logical connectives, and algebra of logic are explained. The part of Chapter 3, “A Machine That Will Think,” that discusses the operations greater-than and selection, also explains some of the algebra of logic. It introduces, for example, the formula
p = T(a > b) = 1, 0
This is a way of saying briefly that the truth value of the statement “a is greater than b” equals p; p is 1 if the statement is true and 0 if the statement is false. The truth value 1 corresponds with “yes.” The truth value 0 corresponds with “no.”
With mechanical brains we are especially interested in handling mathematics and logic without any sharp dividing line between them. For example, suppose that we have a register in which a ten-digit number like 1,765,438,890 may be stored. We should be able to use that register to store a number consisting of only 1’s and 0’s, like 1,100,100,010. Such a number may designate the answers to 10 successive questions: yes, yes, no, no, yes, no, no, no, yes, no. Or it may tell 10 successive binary digits. The register then is three times as useful: it can store either decimal numbers or truth values or binary digits. We need, of course, a way to obtain from the register any desired digit. For this purpose we may have two instructions to the machine: (1) read the left-hand end digit; (2) shift the number around in a circle. The second instruction is the same as multiplying by 10 and then putting the left-most digit at the right-hand end. For example, suppose that we want the 3rd digit from the left in 1,100,100,010. The result of the first circular shift is 1,001,000,101; the result of the second circular shift is 0,010,001,011; and reading the left-most digit gives 0. A process like this has been called extraction and is being built into the newest mechanical brains.
Using truth values, we can put down very neatly some truths of ordinary algebra. For example:
|a| = a · T(a ≥ 0) - a · T(a < 0)
For another example:
T(a > b) + T(a = b) + T(a < b) = 1
[Pg 223] Many common logical operations, like selecting and comparing, and the behavior of many simple mechanisms, like a light or a lock, can be expressed by truth values. Chapter 4, on punch-card mechanisms, contains a number of examples.
In ordinary language, a pronoun, like “he,” “she,” “it,” “the former,” “the latter,” is a word that usually stands for a noun previously referred to. A pronoun usually stands for the last preceding noun that the grammar allows. In mathematics, a variable, like “a,” “b,” “x,” “m₁,” “m₂” closely resembles a pronoun in ordinary language. A variable is a symbol that usually stands for a number previously referred to, and usually it stands for the same number throughout a particular discussion.
| In the Equation |
The Name of a is: |
The Name of b is: |
The Name of c is: |
|---|---|---|---|
| a + b = c | augend | addend | sum |
| a - b = c | minuend | subtrahend | remainder |
| a × b = c | multiplicand | multiplier | product |
| a ÷ b = c | dividend | divisor | quotient |
Augend and addend are names of registers in the Harvard Mark II calculator (see Chapter 10).
Two digits that add to 9 (0 and 9, 1 and 8, 2 and 7, 3 and 6, 4 and 5) are called nines complements of each other. The nines complement of a number a is the number b in which each digit of b is the nines complement of the corresponding digit of a; for example, the nines complement of 173 is 826. Ordinary subtraction is the same as addition as of the nines complement, with a simple correction; for example, 562 less 173 (equal to 389) is the same as 562 plus 826 (equal to 1388) less 1000 plus 1.
The correction “less 1000 plus 1” of the foregoing example may be thought of as carrying the 1 (in the result 1388) around from the left-hand end to the right-hand end, where it is there added. So the 1 is called end-around-carry. [Pg 224]
Two digits that add to 10 are called tens complements of each other. The tens complement of a number a, however, is equal to the nines complement of the number plus 1. For example, the tens complement of 173 is 827. When subtracting by adding a tens complement, the left-most digit 1 in the result is dropped. For example, 562 less 173 (equal to 389) is the same as 562 plus 827 (equal to 1389) less 1000.
A power of any number a is a multiplied by itself some number of times. a × a × a ... × a where a appears b times is written aᵇ and is read a to the bth power. a², a to the 2nd power, is a × a and is called a squared or the square of a. a³, a to the 3rd power, a × a × a, is called a cubed, or the cube of a. a⁰, a to the zero power, is equal to 1 for every a. a¹, a to the power 1, is a itself. The first power is often called linear. a to some negative power is the same as 1 divided by that power; that is, a⁻ᵇ = 1/aᵇ. a⁻¹, a to the power minus 1, is 1/a, and is called the reciprocal of a. a¹ᐟ², a to the one-half power, is a number c such that c × c = a, and is called the square root of a and often denoted by √a.
An example of a table is:
| 0.025 | 0.03 | |
| 1 | 1.02500 | 1.03000 |
| 2 | 1.05063 | 1.06090 |
| 3 | 1.07689 | 1.09273 |
The numbers in the body of the table, called tabular values, depend on or are determined by the numbers along the edge of the table, called arguments. In this example, if 1, 2, 3 are choices of a number n, and if 0.025, 0.03 are choices of a number i, then each tabular value y is equal to 1 plus i raised to the nth power. n and i are also called independent variables, and y is called the dependent variable. The table expresses a function or formula or rule. The rule could be stated as: add i to 1; raise the result to the nth power.
A number is said to be a constant if it has the same value under all conditions. For example, in the formula:
(area of a circle) = π × (radius)²,
π is a constant, equal to 3.14159 ...,
applying equally well to all circles. [Pg 225]
Mathematics recognizes several kinds of infinity. One of them occurs when numbers become very large. For example, the quotient of 12 divided by a number x, as x becomes closer and closer to 0, becomes indefinitely large, and the limit is called infinity and is denoted ∞.
An example of two linear simultaneous equations is:
7x + 8t = 22
3x + 5t = 11
x and t are called unknowns—that is, unknown variables—because the objective of solving the equations is to find them. These equations are called simultaneous because they are to be solved together, at the same time, for values of x and t which will fit in both equations. The equations are called linear because the only powers of the unknowns that appear are the first power. Values that solve equations are said to satisfy them. It is easy to solve these two equations and find that x = 2 and t = 1 is their solution. But it is a long process to solve 10 linear simultaneous equations in 10 unknowns, and it is almost impossible (without using a mechanical brain) to solve 100 linear simultaneous equations in 100 unknowns.
See the sections in Chapter 5 entitled “Differential Equations,” “Physical Problems,” and “Solving Physical Problems.” There these ideas and, to some extent, also the following ideas were explained: formula, equation, function, differential function, instantaneous rate of change, interval, inverse, integrating. See also a textbook on calculus. If y is a function of x, then a mathematical symbol for the derivative of y with respect to x is Dₓ y, and a symbol for the integral of y with respect to x, is ∫y dx. An integral with given initial conditions (see p. 83) is a definite integral.
A famous mathematical function is the exponential. It equals the constant e raised to the x power, eˣ, where e equals 2.71828.... The exponential lies between the powers of 2 and the powers of 3. It can be computed from:
| eˣ = 1 + | x² | + | x³ | + . . . |
| 1 · 2 | 1 · 2 · 3 |
[Pg 226] It is a solution of the differential equation Dₓy = y. See also a textbook on calculus. The exponential to the base 10 is 10ˣ.
Another important mathematical function is the logarithm. It is written log x or logₑ x and can be computed from the two equations:
log uv = log u + log v
| log(1 + x) = x - | x² | + | x³ | - . . . x² < 1 |
| 2 | 3 |
It is a solution of the differential equation Dₓy = 1/y. If y is the logarithm of x, then x is the antilogarithm of y. The logarithm to the base 10 of x, log₁₀ x, equals the logarithm to the base e of x, logₑ x, divided by logₑ 10. See also textbooks on algebra and calculus.
These also are important mathematical functions. The sine and cosine are solutions of the differential equation Dₓ(Dₓy) =-y and are written as sin x and cos x. They can be computed from
| sin x = x - | x³ | + | x⁵ | - . . . |
| 1 · 2· 3 | 1 · 2 · 3· 4· 5 | |||
| cos x = 1 - | x² | + | x₄ | - . . . |
| 1 · 2 | 1 · 2 · 3· 4 | |||
The tangent of x is simply sine of x divided by cosine of x. If y is the tangent of x, then x is the antitangent of y. See also references on trigonometry and on calculus. Trigonometric tables include sine, cosine, tangent, and related functions.
These are mathematical functions that were named after Friedrich W. Bessel, a Prussian astronomer who lived from 1784 to 1846. Bessel functions are found as some of the solutions of the differential equation
x² Dₓ(Dₓy) + x Dₓy + (x² - n²)y = O
This equation arises in a number of physical problems in the fields of electricity, sound, heat flow, air flow, etc. [Pg 227]
A matrix is a table (or array) of numbers in rows and columns, for which addition, multiplication, etc., with similar tables is specially defined. For example, the matrix
| 1 | 2 | |
| 3 | 4 |
plus the matrix
| 5 | 20 | |
| 60 | 100 |
equals the matrix
| 6 | 22 | |
| 63 | 104 |
(Can you guess the rule defining addition?)
Calculations using matrices are useful in physics, engineering, psychology, statistics, etc. To add a square matrix of 100 terms in an array of 10 columns and 10 rows to another such matrix, 100 ordinary additions of numbers are needed. To multiply one such matrix by another, 1000 ordinary multiplications and 900 ordinary additions are needed. See references on matrix algebra and matrix calculus.
On p. 221, a sequence of values of y is shown: 26, 37, 50, 65, 82. Suppose, however, the second value of y was reported as 47 instead of 37. Then the differences of y as we pass down the sequence would not be 11, 13, 15, 17 (which is certainly regular or smooth) but 21, 3, 15, 17 (which is certainly not smooth). The second set of differences would strongly suggest a mistake in the reporting of y. The smoothness of differences is often a useful check on a sequence of reported values.
[Pg 228]
A book like the present one can cover only a part of the subject of machines that think. To obtain more information about these machines and other topics to which they are related there are many references that may be consulted. There are still few books directly on the subject of machines that think, but there are many articles and papers, most of them rather specialized.
The purpose of this supplement is to give a number of these references and to provide a brief, general introduction to some of them. The references are subdivided into groups, each dealing with a branch of the subject. The references in each group are in alphabetical order by name of author (with “anonymous” last), and under each author they are in chronological order by publication date. Some publications, especially a forum or symposium, are listed more than once, according as the topic discussed falls in different groups. In this supplement, the sign three dots ( ...) next to the page numbers for an article indicates that the article is continued on later, nonconsecutive pages.
It seemed undesirable to try to make the group of references dealing with a subject absolutely complete, so long as enough were given to provide a good introduction to the subject. It proved impractical to try to make the citation of every single reference technically complete, so long as enough citation was given so that the reference could certainly be found. Furthermore, in a list of more than 250 references, errors are almost certain to occur. If any reader should send me additions or corrections, I shall be more than grateful. [Pg 229]
No one yet knows specifically how particular ideas are thought about in the human brain. The references listed in this section, however, contain some information about such topics as:
The structural differences, development, and evolution of the brains of animals, apes, primitive man, and modern man.
The effect on the brain of blood composition, body temperature, supply of oxygen, and other biochemical factors.
The structure and physiology of the brain, the nervous system, and nerve impulses.
The theory of learning, intelligence, and memory.
Barcroft, Joseph, The Brain and Its Environment, New Haven: Yale University Press, 1948, 117 pp.
Beach, Frank A., Payday for Primates, Natural History, vol. 56, no. 10, Dec. 1947, pp. 448-451.
Beach, Frank A., Can Animals Reason? Natural History, vol. 57, no. 3, Mar. 1948, pp. 112-116 ...
Berry, R. J. A., Brain and Mind, or the Nervous System of Man, New York: The Macmillan Co., 1928, 608 pp.
Boring, Edwin G., A History of Experimental Psychology, New York: Century Co., 1929, 699 pp.
Franz, Shepherd I., The Evolution of an Idea; How the Brain Works, Los Angeles: University of California, 1929, 35 pp.
Herrick, C. Judson, The Thinking Machine, Chicago: University of Chicago Press, 1929, 374 pp.
Herrick, C. Judson, Brains of Rats and Men, Chicago: University of Chicago Press, 1930, 382 pp.
Lashley, Karl S., Brain Mechanisms and Intelligence, Chicago: University of Chicago Press, 1929, 186 pp.
Pieron, Henri, Thought and the Brain, London: Kegan, Paul, Trench, Trübner & Co., 1927, 262 pp. Also New York: Harcourt, Brace & Co.
Schrödinger, Erwin, What is Life?, New York: The Macmillan Co., 1945, 90 pp.
Sherrington, Charles S., The Brain and Its Mechanism, Cambridge, England: The University Press, 1933, 35 pp.
Tilney, Frederick, The Brain from Ape to Man, New York: P. B. Hoeber, Inc., 1928, 2 vol., 1075 pp.
Wiener, Norbert, Cybernetics, or Control and Communication in the Animal and the Machine, New York: John Wiley & Sons, 1948, 194 pp.
Anonymous, Ten Billion Relays, Time, Feb. 14, 1949, p. 67.
[Pg 230]
There has recently been another approach to the problem: How does a brain think? A group of men, many of them in and near Chicago, have been saying: “We know the properties of nerves, nerve impulses, and simple nerve networks. We know the activity of the brain. What mathematical model of nerve networks is necessary to account for the activity of the brain?” These men have used mathematics, statistics, and mathematical logic in the effort to attack this problem, and they support a Bulletin of Mathematical Biophysics.
Householder, Alston S., A Neural Mechanism for Discrimination, Psychometrika, vol. 4, no. 1, Dec. 1939, pp. 45-58.
Householder, Alston S., and Herbert D. Landahl, Mathematical Biophysics of the Central Nervous System, Bloomington, Ind.: Principia Press, 1945.
Landahl, Herbert D., Contributions to the Mathematical Biophysics of the Central Nervous System, Bulletin of Mathematical Biophysics, vol. 1, no. 2, June 1939, pp. 95-118.
Landahl, Herbert D., Warren S. McCulloch, and Walter Pitts, A Statistical Consequence of the Logical Calculus of Nervous Nets, Bulletin of Mathematical Biophysics, vol. 5, no. 4, Dec. 1943, pp. 135-137.
Landahl, Herbert D., A Note on the Mathematical Biophysics of Central Excitation and Inhibition, Bulletin of Mathematical Biophysics, vol. 7, no. 4, Dec. 1945, pp. 219-221.
Lettvin, Jerome Y., and Walter Pitts, A Mathematical Theory of the Affective Psychoses, Bulletin of Mathematical Biophysics, vol. 5, no. 4, Dec. 1943, pp. 139-148.
McCulloch, Warren S., and Walter Pitts, A Logical Calculus of the Ideas Immanent in Nervous Activity, Bulletin of Mathematical Biophysics, vol. 5, no. 4, Dec. 1943, pp. 115-133.
Rashevsky, N., Mathematical Biophysics, Chicago: University of Chicago Press. Revised edition, 1948, 669 pp.
Rashevsky, N., Mathematical Biophysics of Abstraction and Logical Thinking, Bulletin of Mathematical Biophysics, vol. 7, no. 3, Sept. 1945, pp. 133-148.
Rashevsky, N., Some Remarks on the Boolean Algebra of Nervous Nets in Mathematical Biophysics, Bulletin of Mathematical Biophysics, vol. 7, no. 4, Dec. 1945, pp. 203-211.
Rashevsky, N., A Suggestion for Another Statistical Interpretation of the Fundamental Equations of the Mathematical Biophysics of the Central Nervous System, Bulletin of Mathematical Biophysics, vol. 7, no. 4, Dec. 1945, pp. 223-226.
Rashevsky, N., The Neural Mechanism of Logical Thinking, Bulletin of Mathematical Biophysics, vol. 8, no. 1, Mar. 1946, pp. 29-40.
[Pg 231]
Hardly any field of techniques for thinking is more fascinating than language. The following list of references, of course, is short; it is meant chiefly as an introduction pointing out a number of different paths into the field of language and languages. Such topics as the following are introduced by the references in this list:
Bloomfield, Leonard, Language, New York: Henry Holt & Co., 1933, 564 pp.
Bodmer, Frederick, and Launcelot Hogben, The Loom of Language, New York: W. W. Norton & Co., 1944, 692 pp.
Flesch, Rudolf, The Art of Plain Talk, New York: Harper & Brothers, 1946, 210 pp.
Graff, Willem L., Language and Languages: An Introduction to Linguistics, New York: D. Appleton & Co., 1932, 487 pp.
Hayakawa, S. I., Language in Action, New York: Harcourt, Brace & Co., 1941, 345 pp.
Jespersen, Otto, The Philosophy of Grammar, New York: Henry Holt & Co., 1929 (third printing), 359 pp.
Jespersen, Otto, Analytic Syntax,
In this book, by means of a well-contrived system of letters and signs, the great linguistic scholar Jespersen depicts all the important inter-relations of English words and parts of words in connected speech.
Ogden, C. K., The System of Basic English, New York: Harcourt, Brace & Co., 1934, 320 pp.
Schlauch, Margaret, The Gift of Tongues, New York: Modern Age Books, 1942, 342 pp.
Walpole, Hugh R., Semantics: The Nature of Words and Their Meanings, New York: W. W. Norton & Co., 1941, 264 pp.
[Pg 232]
For many years, nearly all references about machines as a language for thinking have been specialized and limited. Colleges with scholars who write textbooks usually have not had a variety of expensive and versatile computing machinery. As a result, the main environment for stimulating possible authors has until recently been missing. The list of references is accordingly brief.
Aiken, Howard H., and others, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, 302 pp.
Comrie, John Leslie, The Application of Commercial Calculating Machines to Scientific Computing, Mathematical Tables and Other Aids to Computation, vol. 2, no. 16, Oct. 1946, pp. 149-159.
Crew, E. W., Calculating Machines, The Engineer, vol. 172, Dec. 1941, pp. 438-441.
Fry, Macon, Designing Computing Mechanisms, Cleveland, Ohio: Penton Publishing Co., 1946, 48 pp. (Reprinted from Machine Design, Aug. 1945 through Feb. 1946.)
Hartree, D. R., Calculating Machines: Recent and Prospective Developments and Their Impact on Mathematical Physics, Cambridge, England: The University Press, 1947, 40 pp.
Horsburgh, E. H., Modern Instruments and Methods of Calculation, London: G. Bell and Sons, Ltd., 1914, 343 pp.
Lilley, S., Mathematical Machines, Nature, vol. 149, Apr. 25, 1942, pp. 462-465.
Murray, Francis J., The Theory of Mathematical Machines, New York: King’s Crown Press, 1947, 116 pp.
The author states that a mathematical machine is a mechanism that provides information concerning the relationships among a specified set of mathematical concepts.
Turck, J. A. V., The Origin of Modern Calculating Machines, Chicago: Western Society of Engineers, 1921.
Recently, however, some magazine and newspaper publishers have seen news value in machines that think, and some good general articles with appeal to a wide audience have appeared. For the references to these articles, see the section of this supplement entitled “Digital Machines—Miscellaneous.”
There are a few general references on punch-card calculating machines: [Pg 233]
Baehne, G. Walter, editor, and others, Practical Applications of the Punched Card Method in Colleges and Universities, New York: Columbia University Press, 1935, 442 pp.
This is a collection of many contributions from a number of authors, describing various applications, chiefly educational.
Eckert, W. J., Punched-Card Methods in Scientific Computation, New York: Columbia University, The Thomas J. Watson Astronomical Computing Bureau, 1940, 136 pp.
This is a scientific treatise, chiefly relating to the computation of orbits in astronomy.
Hartkemeier, Harry Pelle, Principles of Punch-Card Machine Operation (Subtitle: How to Operate Punch-Card Tabulating and Alphabetic Accounting Machines), New York: Thomas Y. Crowell Co., 1942, 269 pp.
This is based on the author’s experience in teaching statistical analysis using IBM tabulators. The book does not deal with the collator or multiplying punch.
Hedley, K. J., The Development of the Punched-Card Method, Actuarial Society of Australasia, 1946, 20 pp.
International Business Machines Corporation, International Business Machines (form no. A-4036-6-45), New York: International Business Machines Corporation, 1945, 65 pp.
Pages 6 to 31 show pictures and brief descriptions of about 20 punch-card machines, available in 1945.
Schnackel, H. G., and H. C. Lang, Accounting by Machine Methods, New York: Ronald Press Co., 1939, 53 pp.
Wolf, Arthur W., and Edmund C. Berkeley, Advanced Course in Punched Card Operations, Newark, N. J.: Prudential Insurance Company of America, 1942, 98 pp.
A useful and authoritative description of IBM punch-card calculating machinery is the following:
International Business Machines Corporation, Department of Education, Machine Methods of Accounting, Endicott, N. Y.: International Business Machines Corporation, 1936-41, 385 pp.
This is a collection of 28 separate booklets telling the detailed operation of IBM punch-card machinery. They were written for employees of IBM and users of IBM equipment. The following list of the booklets is useful in locating them:
[Pg 234]
| Title | Form No. | Date | No. of Pages |
|---|---|---|---|
| Machine Methods of Accounting—Foreword | AM | 1936 | 6 |
| Development of IBM Corporation | AM-1-1 | 1936 | 14 |
| Principles of the Electric Accounting Machine Method | AM-2 | 1936 | 12 |
| The Tabulating Card | AM-3-1 | 1936 | 20 |
| Design of Tabulating Cards | AM-4-1 | 1936 | 16 |
| Preparation and Use of Codes | AM-5 | 1936 | 28 |
| Organization and Supervision of the Tabulating Department | AM-6 | 1936 | 16 |
| Selection and Training of Key Punch Operators | AM-7 | 1936 | 12 |
| Accounting Control | AM-8 | 1936 | 8 |
| Punches | AM-9 | 1936 | 12 |
| Alphabetic Printing Punches | AM-10 | 1936 | 7 |
| Facts to Know about Key Punches | AM-11 | 1936 | 4 |
| Verifiers | AM-12 | 1936 | 4 |
| Gang Punches | AM-13 | 1936 | 8 |
| Card-Operated Sorting Machines | AM-14 | 1936 | 12 |
| Facts to Know about Sorters | AM-14a | 1936 | 4 |
| Electric Tabulating Machines | AM-15 | 1936 | 20 |
| Electric Accounting Machines (Type 285 and Type 297) | AM-16 | 1936 | 16 |
| Alphabetic Direct Subtraction Accounting Machine | AM-17 | 1936 | 28 |
| Numerical Interpreters | AM-18 | 1936 | 8 |
| Electric Punched-Card Interpreter (Type 552) | AM-18a | 1941 | 8 |
| Reproducing Punches (Type 512) | AM-19 | 1936 | 16 |
| Automatic Summary Punches for Use with | |||
| the Numerical Accounting Machines (Type 285-297) | AM-20 | 1936 | 16 |
| Automatic Summary Punches for Use with the | |||
| Alphabetic Accounting Machines (Type 405) | AM-20a | 1940 | 16 |
| Multiplying Punches | AM-21 | 1936 | 16 |
| Application of Machines to Accounting Functions | AM-22 | 1936 | 24 |
| Other International Products | AM-23-2 | 1936 | 19 |
| The International Automatic Carriage (Type 921) | AM-24 | 1938 | 15 |
The Department of Education of IBM has begun a second series of booklets on the principles of operation of punch-card calculating machinery:
International Business Machines Corporation, Department of Education, Principles of Operation, Endicott, N. Y.: International Business Machines Corporation, 1942 and later (except for one published in 1939).
Many of the booklets in this series have good examples of machine operation and applications. Also, for the first time, letters and numbers have been used as coordinates to label the hubs on the plugboards. This series includes the following: [Pg 235]
| Title | Form No. | Date | No. of Pages |
|---|---|---|---|
CARD PUNCHES AND VERIFIERS |
|||
| Card-Punching and Verifying Machines | 52-3176-0 | 1946 | 21 |
| Alphabetical Verifier, Type 055 | 52-3295-1 | 1946 | 4 |
INTERPRETERS |
|||
| Card Interpreters, Type 550, 551, and 552 | 52-3178-0 | 1946 | 14 |
REPRODUCERS |
|||
| Automatic Reproducing Punch, Type 513 | 52-3180-0 | 1945 | 22 |
| End Printing Reproducing Punch, Type 519 | 52-3292-1 | 1946 | 26 |
| Electric Document-Originating Machine, | June | ||
| Type 519 | 52-3292-2 | 1948 | 26 |
COLLATORS |
|||
| Collator | AM-25 | 1943 | 31 |
| Collator Counting Device | C.R. 9178 | 1942 | 12 |
CALCULATING PUNCHES |
|||
| Electric Multiplier, Type 601 | 52-3408-1 | 1947 | 47 |
| Calculating Punch, Type 602 | 52-3409-0 | 1946 | 83 |
| Calculating Punch, Type 602 | 52-3409-5 | 1947 | 93 |
| Calculating Punch, Type 602-A (Preliminary Manual) | 22-5489-0 | 1948 | 59 |
| Electronic Multiplier, Type 603 | 52-3561-0 | 1946 | 5 |
| Electronic Calculating Punch, Type 604 | 22-5279-0 | 1948 | 51 |
TABULATORS |
|||
| Accounting Machine, Type 402 and 403 (Preliminary Manual) | 22-5654-0 | 1949 | 146 |
| Alphabetical Accounting Machine, Type 404 | 52-3395-1 | 1946 | 96 |
| Typical Applications, Alphabetical Accounting Machine, | |||
| Type 404, with Multiple Line Printing | 22-3771-1 | 1947 | 47 |
| Alphabetical Accounting Machine, Type 405 | AM 17 (1), | 1943 | 90 |
| Revised | 1/1/43 | ||
| Alphabetical Accounting Machine, | Nov. | ||
| Type 405 | 52-3179-2 | 1948 | 81 [Pg 236] |
AUTOMATIC PRINTING CARRIAGES |
|||
| Bill Feed, Type 920 | 52-3184-0 | 1945 | 21 |
| Form Feeding Device | 52-3235-0 | 1946 | 11 |
| Automatic Carriage, Type 921 | 52-3183-0 | 1945 | 36 |
| Tape-Controlled Carriage | |||
| (Preliminary Manual, Revised) | 22-5415-1 | 1948 | 27 |
TEST SCORING MACHINE |
|||
| Test Scoring Machine | 94-2333-0 | 1939 | 19 |
| May | |||
| Test Scoring Machine | 32-9145-1 | 1946 | 20 |
| Published Tests Adapted for Use with | June | ||
| the IBM Electric Test Scoring Machine | 27-4286-9 | 1948 | 8 |
In addition to the new types of punch-card machines referred to in the above list, an elaborate punch-card calculating machine is described in the following reference:
Eckert, W. J., The IBM Pluggable Sequence Relay Calculator, Mathematical Tables and Other Aids to Computation, vol. 3, no. 23, July 1948, pp. 149-161.
A description of punch-card machinery in rather a light vein is contained in:
Anonymous, Speaking of Pictures: New Mechanical Monsters Ease Life’s Growing Pains, Life, Sept. 15, 1947, pp. 15-16.
Anonymous, 540, Chicago: Time-Life-Fortune Magazine, Subscription Fulfillment Office, 1948, 15 pp.
New types of punch-card machinery are continually coming into use. Among them are: machines that take in punch cards and make punched paper tape (such as teletype tape), and vice versa—useful for transmitting punch-card information over wires; an electric typewriter operated by punch cards—useful for preparing almanacs for sea and air navigation, etc.; a calculator programmed by punch cards, consisting of an assembly of a tabulator, an electronic calculating punch, and an auxiliary storage unit, all cabled together—useful for some types of long calculation; etc. For information about such machinery, the manufacturers may be consulted.
There are many articles in scientific journals on applications of punch-card calculating machinery to technical problems. The fields of [Pg 237] engineering, education, indexing, mathematics, surveying, statistics, and others are all represented in the following list of sample references:
Alt, Franz L., Multiplication of Matrices, Mathematical Tables and Other Aids to Computation, vol. 2, no. 13, Jan. 1946, pp. 12-13.
Bailey, C. F., and others, Punch Cards for Indexing Scientific Data, Science, vol. 104, Aug. 23, 1946, p. 181.
Bower, E. C., On Subdividing Tables, Lick Observatory Bulletin, vol. 16, no. 455, Nov. 1933, pp. 143-144.
Bower, E. C., Systematic Subdivision of Tables, Lick Observatory Bulletin, vol. 17, no. 467, Apr. 1935, pp. 65-74.
Clemence, G. M., and Paul Herget, Optimum-Interval Punched-Card Tables, Mathematical Tables and Other Aids to Computation, vol. 1, no. 6, Apr. 1944, pp. 173-176.
Culley, Frank L., Use of Accounting Machines for Mass-Transformation from Geographic to Military-Grid Coordinates, Washington, D. C.: National Research Council, American Geophysical Union Transactions of 1942, part 2, pp. 190-197.
Deming, W. Edwards, and Morris H. Hansen, On Some Census Aids to Sampling, Journal of the American Statistical Association, vol. 38, no. 225, Sept. 1943, pp. 353-357.
Dunlap, Jack W., The Computation of Means, Standard Deviations, and Correlations by the Tabulator When the Numbers Are Both Positive and Negative, Proceedings of the Educational Research Forum, International Business Machines Corporation, Aug. 1940, pp. 16-19.
Dwyer, Paul S., The Use of Tables in the Form of Prepunched Cards, Proceedings of the Educational Research Forum, International Business Machines Corporation, Aug. 1940, pp. 125-127.
Dwyer, Paul S., Summary of Problems in the Computation of Statistical Constants with Tabulating and Sorting Machines, Proceedings of the Educational Research Forum, International Business Machines Corporation, Aug. 1940, pp. 20-28.
Dwyer, Paul S., and Alan D. Meacham, The Preparation of Correlation Tables on a Tabulator Equipped with Digit Selection, Journal of the American Statistical Association, vol. 32, 1937, pp. 654-662.
Dyer, H. S., Making Test Score Data Effective in the Admission and Course Placement of Harvard Freshmen, Proceedings of the Research Forum, International Business Machines Corporation, 1946, pp. 55-62.
Eckert, W. J., and Ralph F. Haupt, The Printing of Mathematical Tables, Mathematical Tables and Other Aids to Computation, vol. 2, no. 17, Jan. 1947, pp. 196-202.
Feinstein, Lillian, and Martin Schwarzchild, Automatic Integration of Linear Second-Order Differential Equations by Means of Punched-Card Machines, Review of Scientific Instruments, vol. 12, no. 8, Aug. 1941, pp. 405-408.
Hotelling, Harold, Some New Methods in Matrix Calculation, The Annals of Mathematical Statistics, vol. 14, no. 1, Mar. 1943, pp. 1-34. [Pg 238]
International Business Machines Corporation, editor, and others, Proceedings of the Educational Research Forum, Endicott, N. Y.: International Business Machines Corporation, 1941.
International Business Machines Corporation, editor, and others, Proceedings of the Research Forum, Endicott, N. Y.: International Business Machines Corporation, 1946, 94 pp.
King, Gilbert W., Punched-Card Tables of the Exponential Function, Review of Scientific Instruments, vol. 15, no. 12, Dec. 1944, pp. 349-350.
King, Gilbert W., and George B. Thomas, Preparation of Punched-Card Tables of Logarithms, Review of Scientific Instruments, vol. 15, no. 12, Dec. 1944, p. 350.
Kormes, Mark, A Note on the Integration of Linear Second-Order Differential Equations by Means of Punched Cards, Review of Scientific Instruments, vol. 14, no. 4, Apr. 1943, p. 118.
Kormes, Mark, Numerical Solution of the Boundary Value Problem for the Potential Equation by Means of Punched Cards, Review of Scientific Instruments, vol. 14, no. 8, Aug. 1943, pp. 248-250.
Kormes, Mark, and Jennie P. Kormes, Numerical Solution of Initial Value Problems by Means of Punched-Card Machines, Review of Scientific Instruments, vol. 16, no. 1, Jan. 1945, pp. 7-9.
Kuder, G. Frederic, Use of the IBM Scoring Machine for Rapid Computation of Tables of Intercorrelations, Journal of Applied Psychology, vol. 22, no. 6, Dec. 1938, pp. 587-596.
Maxfield, D. K., Library Punched Card Procedures, Library Journal, vol. 71, no. 12, June 15, 1946, pp. 902-905 ...
McLaughlin, Kathleen, Adding Machines Nip AEF Epidemics, New York: New York Times, Apr. 27, 1945.
McPherson, John C., On Mechanical Tabulation of Polynomials, Annals of Mathematical Statistics, Sept. 1941, pp. 317-327.
McPherson, John C., Mathematical Operations with Punched Cards, Journal of the American Statistical Association, vol. 37, June 1942, pp. 275-281.
Milliman, Wendell A., Mechanical Multiplication by the Use of Tabulating Machines, Transactions of the Actuarial Society of America, vol. 35, part 2, Oct. 1934, pp. 253-264; for discussion see also vol. 36, part 1, May 1935, pp. 77-84.
Royer, Elmer B., A Machine Method for Computing the Biserial Correlation Coefficient in Item Validation, Psychometrika, vol. 6, no. 1, Feb. 1941, pp. 55-59.
Whitten, C. A., Triangulation Adjustment by International Business Machines, Washington, D. C.: National Research Council, American Geophysical Union Transactions of 1943, part 1, p. 31.
The following bibliography may be obtained on request to the Watson Scientific Computing Laboratory, Columbia University, 612 West 116 Street, New York 27, N. Y.: [Pg 239]
Watson Scientific Computing Laboratory, Bibliography: The Use of IBM Machines in Scientific Research, Statistics, and Education, New York: International Business Machines Corporation (form no. 50-3813-0), Sept. 1947, 25 pp.
The organization and equipment of this laboratory are described in:
Eckert, W. J., Facilities of the Watson Scientific Computing Laboratory, Proceedings of the Research Forum, International Business Machines Corporation, 1946, pp. 75-80.
The basic scientific articles on the two differential analyzers at Massachusetts Institute of Technology are:
Bush, Vannevar, The Differential Analyzer: A New Machine for Solving Differential Equations, Journal of the Franklin Institute, vol. 212, no. 4, Oct. 1931, pp. 447-488.
Bush, Vannevar, and Samuel H. Caldwell, A New Type of Differential Analyzer, Journal of the Franklin Institute, vol. 240, no. 4, Oct. 1945, pp. 255-326.
Some of the less technical articles about the second differential analyzer at M.I.T. are:
Caldwell, Samuel H., Educated Machinery, Technology Review, vol. 48, no. 1, Nov. 1945, pp. 31-34.
Genet, N., 100-Ton Brain at M.I.T., Scholastic, vol. 48, Feb. 4, 1946, p. 36.
Anonymous, Mathematical Machine; New Electronic Differential Analyzer, Science News Letter, vol. 48, Nov. 10, 1945, p. 291.
Anonymous, Robot Einstein: Differential Analyzer at M.I.T., Newsweek, vol. 26, Nov. 12, 1945, p. 93.
Anonymous, M.I.T.’s 100-Ton Mathematical Brain is Now to Tackle Problems of Peace, Popular Science, vol. 148, Jan. 1946, p. 81.
Anonymous, The Great Electro-Mechanical Brain; M.I.T.’s Differential Analyzer, Life, vol. 20, Jan. 14, 1946, pp. 73-74 ...
Anonymous, All the Answers at Your Fingertips; in the Laboratory of M.I.T., Popular Mechanics, vol. 85, Mar. 1946, pp. 164-167 ...
A differential analyzer was built at the Moore School of Electrical Engineering:
Travis, Irven, Differential Analyzer Eliminates Brain Fag, Machine Design, July 1935, pp. 15-18.
A differential analyzer was built at the General Electric Company, Schenectady, N. Y. Instead of using a mechanical or electrical amplifier of the motion of the little turning wheel riding on the disc, [Pg 240] this machine follows the motion using polarized light. This machine is described in:
Berry, T. M., Polarized Light Servo System, Transactions of the American Institute of Electrical Engineers, vol. 63, Apr. 1944, pp. 195-197.
Kuehni, H. P., and H. A. Peterson, A New Differential Analyzer, Transactions of the American Institute of Electrical Engineers, vol. 63, May 1944, pp. 221-227.
A differential analyzer has been put into use at the University of California:
Boelter, L. M. K., and others, The Differential Analyzer of the University of California, Los Angeles: University of California, 1947, 25 pp.
A differential analyzer was built at Manchester University, England. It was built first from “Meccano” parts, at a total cost of about 20 pounds, and later refined for more exact work. Some articles dealing with this differential analyzer are:
Hartree, D. R., The Differential Analyzer, Nature, vol. 135, June 8, 1935, p. 940.
Hartree, D. R., The Mechanical Integration of Differential Equations, The Mathematical Gazette, vol. 22, 1938, pp. 342-364.
Hartree, D. R., and A. Porter, The Construction of a Model Differential Analyser, Memoirs and Proceedings of the Manchester Literary and Philosophical Society, vol. 79, July 1935, pp. 51-72.
Other small scale differential analyzers built in England are covered in:
Beard, R. E., The Construction of a Small Scale Differential Analyser and Its Application to the Calculation of Actuarial Functions, Journal of the Institute of Actuaries, vol. 71, 1942, pp. 193-227.
Massey, H. S. W., J. Wylie, and R. A. Buckingham, A Small Scale Differential Analyser: Its Construction and Operation, Proceedings of the Royal Irish Academy, vol. 45, 1938, pp. 1-21.
A differential analyzer constructed in Germany is briefly described in the following:
Sauer, R., and H. Poesch, Integrating Machine for Solving Ordinary Differential Equations, Engineers Digest (American Edition), vol. 1, May 1944, pp. 326-328.
From the historical point of view there are some interesting papers on a machine for solving differential equations by Sir William Thomson (Lord Kelvin), including one by his brother James Thomson. They are in the Proceedings of the Royal Society, vol. 24, Feb. 1876, pp. 262-275. The method of integration by a machine is described, but the [Pg 241] state of machine tools at the time was such that no accurate mechanism was constructed. Another interesting paper foreshadowing the differential analyzer is:
Wainwright, Lawrence L., A Ballistic Engine, Chicago: University of Chicago, thesis for Master’s Degree, 1923, 28 pp.
Some of the applications and mathematical limitations of differential analyzers are covered in:
Bush, V., and S. H. Caldwell, Thomas-Fermi Equation Solution by the Differential Analyzer, Physical Review, vol. 38, no. 10, 1931, pp. 1898-1902.
Hartree, D. R., A Great Calculating Machine: the Bush Differential Analyser and Its Applications in Science and Industry, Proceedings of the Royal Institution of Great Britain, vol. 31, 1940, pp. 151-170.
Hartree, D. R., and A. Porter, The Application of the Differential Analyser to Transients on a Distortionless Transmission Line, Journal of the Institute of Electrical Engineering, vol. 83, no. 503, Nov. 1938, pp. 648-656.
Hartree, D. R., and J. R. Womersley, A Method for the Numerical or Mechanical Solution of Certain Types of Partial Differential Equations, Proceedings of the Royal Society of London, series A, vol. 161, 1937, pp. 353-366.
Maginniss, F. J., Differential Analyzer Applications, General Electric Review, vol. 48, no. 5, May 1945, pp. 54-59.
Shannon, Claude E., Mathematical Theory of the Differential Analyzer, Journal of Mathematics and Physics, Cambridge, Mass.: Massachusetts Institute of Technology, vol. 20, no. 4, 1941, pp. 337-354.
Another branch of the analogue calculating machine is the harmonic analyzer and synthesizer. These are machines that study wave motions and related physical and mathematical functions. A brief list of articles on this type of machine follows:
Archer, R. M., Projecting Apparatus for Compounding Harmonic Vibrations, Journal of Scientific Instruments, vol. 14, 1937, pp. 408-410.
Brown, S. L., A Mechanical Harmonic Synthesizer-Analyzer, Journal of the Franklin Institute, vol. 228, 1939, pp. 675-694.
Brown, S. L., and L. L. Wheeler, A Mechanical Method for Graphical Solution of Polynomials, Journal of the Franklin Institute, vol. 231, 1941, pp. 223-243.
Brown, S. L., and L. L. Wheeler, Use of the Mechanical Multiharmonograph for Graphing Types of Functions and for Solution of Pairs of Non-Linear Simultaneous Equations, Review of Scientific Instruments, vol. 13, Nov. 1942, pp. 493-495. [Pg 242]
Brown, S. L., and L. L. Wheeler, The Use of a Mechanical Synthesizer to Solve Trigonometric and Certain Types of Transcendental Equations, and for the Double Summations Involved in Patterson Contours, Journal of Applied Physics, vol. 14, Jan. 1943, pp. 30-36.
Fürth, R., and R. W. Pringle, A New Photo-Electric Method for Fourier Synthesis and Analysis, London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, vol. 35, series 7, 1944, pp. 643-656.
International Hydrographic Bureau, Tide Predicting Machines, International Hydrographic Bureau, Special Publication 13, July 1926.
Kranz, Frederick W., A Mechanical Synthesizer and Analyzer, Journal of the Franklin Institute, vol. 204, 1927, pp. 245-262.
Marble, F. G., An Automatic Vibration Analyzer, Bell Laboratories Record, vol. 22, Apr. 1944, pp. 376-380.
Maxwell, L. R., An Electrical Method for Compounding Sine Functions, Review of Scientific Instruments, vol. 11, Feb. 1940, pp. 47-54.
Miller, Dayton C., A 32-Element Harmonic Synthesizer, Journal of the Franklin Institute, vol. 181, 1916, pp. 51-81.
Miller, Dayton C., The Henrici Harmonic Analyzer and Devices for Extending and Facilitating Its Use, Journal of the Franklin Institute, vol. 182, 1916, pp. 285-322.
Milne, J. R., A “Duplex” Form of Harmonic Synthetiser and Its Mathematical Theory, Proceedings of the Royal Society of Edinburgh, vol. 39, 1918-19, pp. 234-242.
Montgomery, H. C., An Optical Harmonic Analyzer, Bell System Technical Journal, vol. 17, no. 3, July 1938, pp. 406-415.
Raymond, W. J., An Harmonic Synthesizer Having Components of Incommensurable Period and Any Desired Decrement, Physical Review, vol. 11, series 2, 1918, pp. 479-481.
Robertson, J. M., A Simple Harmonic Continuous Calculating Machine, London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, vol. 13, 1932, pp. 413-419.
Somerville, J. M., Harmonic Synthesizer for Demonstrating and Studying Complex Wave Forms, Journal of Scientific Instruments, vol. 21, Oct. 1944, pp. 174-177.
Straiton, A. W., and G. K. Terhune, Harmonic Analysis by Photographic Method, Journal of Applied Physics, vol. 14, 1943, pp. 535-536.
Wegel, R. L., and C. R. Moore, An Electrical Frequency Analyzer, Bell System Technical Journal, vol. 3, 1924, pp. 299-323.
A third branch of the analogue calculating machine is the network analyzer. To solve problems, this machine uses the laws governing a network of electrical circuits. For example, an electric power company with a system of power lines over hundreds of miles may have a problem about electrical power: will an accident or a sudden demand cause a [Pg 243] breakdown anywhere in the system? In the General Electric Company in Schenectady, N. Y., there is a machine called the A.C. Network Analyzer. All the properties of the power company’s network of lines can be fed on a small scale into the analyzer. Certain dials are turned and certain plugwires are connected. Then various kinds of “accidents” and “sudden demands” are fed into the machine, and the response of the system is noted. The answers given by the machine are multiplied by the proper scale factor, and in this way the problem of the power company is solved.
There are two kinds of problems that network analyzers are built to solve: the steady state conditions and the transient conditions. For example, you may not overload a fuse with an electric iron when it is plugged in and being used, but as you pull out the cord, you may blow the fuse: the steady state does not overstrain the system, but the transient does.
Some articles on network analyzers are:
Enns, W. E., A New Simple Calculator of Load Flow in A.C. Networks, Transactions of the American Institute of Electrical Engineers, vol. 62, 1943, pp. 786-790.
Hazen, H. L., and others, The M.I.T. Network Analyzer, Cambridge, Mass.: Massachusetts Institute of Technology, Department of Electrical Engineering, Serial No. 69, Apr. 1931.
Kuehni, H. P., and R. G. Lorraine, A New A.C. Network Analyzer, Transactions of the American Institute of Electrical Engineers, vol. 57, 1938, pp. 67-73.
Parker, W. W., Dual A.C. Network Calculator, Electrical Engineering, May 1945, pp. 182-183.
Parker, W. W., The Modern A.C. Network Calculator, Transactions of the American Institute of Electrical Engineers, vol. 60, Nov. 1941, pp. 977-982.
Peterson, H. A., An Electric Circuit Transient Analyzer, General Electric Review, Sept. 1939, pp. 394-400.
Varney, R. N., An All-Electric Integrator for Solving Differential Equations, Review of Scientific Instruments, vol. 13, Jan. 1942, pp. 10-16.
Some of the articles on applications of network analyzers to various problems are:
Kron, Gabriel, Equivalent Circuits of the Elastic Field, Journal of Applied Mechanics, vol. A11, Sept. 1944, pp. 146-161.
Kron, Gabriel, Tensorial Analysis and Equivalent Circuits of Elastic Structures, Journal of the Franklin Institute, vol. 238, Dec. 1944, pp. 399-442.
Kron, Gabriel, Numerical Solution of Ordinary and Partial Differential Equations by Means of Equivalent Circuits, Journal of Applied Physics, vol. 16, 1945, pp. 172-186. [Pg 244]
Kron, Gabriel, Electric Circuit Models for the Vibration Spectrum of Polyatomic Molecules, Journal of Chemical Physics, vol. 14, no. 1, Jan. 1946, pp. 19-31.
Kron, G., and G. K. Carter, A.C. Network Analyzer Study of the Schrödinger Equation, Physical Review, vol. 67, 1945, pp. 44-49.
Kron, G., and G. K. Carter, Network Analyzer Tests of Equivalent Circuits of Vibrating Polyatomic Molecules, Journal of Chemical Physics, vol. 14, no. 1, Jan. 1946, pp. 32-34.
Peterson, H. A., and C. Concordia, Analyzers for Use in Engineering and Scientific Problems, General Electric Review, vol. 48, no. 9, Sept. 1945, pp. 29-37.
Another branch of the analogue calculating machine is a type of machine that will solve various kinds of algebraic equations (see Supplement 2). A list of some articles follows. The article by Mallock describes a machine for solving up to 10 linear simultaneous equations in 10 unknowns, and the article by Wilbur, a machine for solving up to 9.
Dietzold, Robert L., The Isograph—A Mechanical Root-Finder, Bell Laboratories Record, vol. 16, no. 4, Dec. 1937, pp. 130-134.
Duncan, W. J., Some Devices for the Solution of Large Sets of Simultaneous Linear Equations, London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 35, series 7, 1944, pp. 660-670.
Frame, J. Sutherland, Machines for Solving Algebraic Equations, Mathematical Tables and Other Aids to Computation, vol. 1, no. 9, Jan. 1945, pp. 337-353.
Hart, H. C., and Irven Travis, Mechanical Solution of Algebraic Equations, Journal of the Franklin Institute, vol. 225, Jan. 1938, pp. 63-72.
Herr, D. L., and R. S. Graham, An Electrical Algebraic Equation Solver, Review of Scientific Instruments, vol. 9, Oct. 1938, pp. 310-315.
Mallock, R. R. M., An Electrical Calculating Machine, Proceedings of the Royal Society, series A, vol. 140, 1933, pp. 457-483.
Mercner, R. O., The Mechanism of the Isograph, Bell Laboratories Record, vol. 16, no. 4, Dec. 1937, pp. 135-140.
Stibitz, George R., Electric Root-finder, Mathematical Tables and Other Aids to Computation, vol. 3, no. 24, Oct. 1948, pp. 328-329.
Wilbur, J. B., The Mechanical Solution of Simultaneous Equations, Journal of the Franklin Institute, vol. 222, Dec. 1936, pp. 715-724.
Some articles referring to various other kinds of analogue machines and their applications are here listed together: [Pg 245]
Bush, V., F. D. Gage, and R. R. Stewart, A Continuous Integraph, Journal of the Franklin Institute, vol. 203, 1927, pp. 63-84.
Gray, T. S., A Photo-Electric Integraph, Journal of the Franklin Institute, vol. 212, 1931, pp. 77-102.
Hazen, H. L., G. S. Brown, and W. R. Hedeman, The Cinema Integraph: A Machine for Evaluating a Parametric Product Integral (two parts and appendix), Journal of the Franklin Institute, vol. 230, July 1940, pp. 19-44, and Aug. 1940, pp. 183-205.
McCann, G. D., and H. E. Criner, Mechanical Problems Solved Electrically, Westinghouse Engineer, vol. 6, no. 2, March 1946, pp. 49-56.
Myers, D. M., An Integraph for the Solution of Differential Equations of the Second-Order, Journal of Scientific Instruments, vol. 16, 1939, pp. 209-222.
Pekeris, C. L., and W. T. White, Differentiation with the Cinema Integraph, Journal of the Franklin Institute, vol. 234, July 1942, pp. 17-29.
Smith, C. E., and E. L. Gove, An Electromechanical Calculator for Directional-Antenna Patterns, Transactions of the American Institute of Electrical Engineers, vol. 62, 1943, pp. 78-82.
Yavne, R. O., High Accuracy Contour Cams, Product Engineering, vol. 19, part 2, Aug. 1948, 3 pp.
Anonymous, Electrical Gun Director Demonstrated, Bell Laboratories Record, vol. 22, no. 4, Dec. 1943, pp. 157-167.
Anonymous, Development of the Electric Director, Bell Laboratories Record, vol. 22, no. 5, Jan. 1944, pp. 225-230.
Anonymous, Old Field Fortune Teller: Electronic Oil Pool Analyzer, Popular Mechanics, vol. 86, Sept. 1946, p. 154.
The basic scientific description of this machine as of September 1, 1945, is contained in:
Aiken, Howard H., and Staff of the Computation Laboratory, A Manual of Operation for the Automatic Sequence-Controlled Calculator, Cambridge, Mass.: Harvard University Press, 1946, 561 pp.
The machine has changed rather a good deal since Sept. 1, 1945. Some circuits have been removed. Other circuits have been added. The capacity of the machine to do problems has been greatly increased. The Computation Laboratory at Harvard University is cordial towards scientific inquiries, and some unpublished, mimeographed information is available at the laboratory regarding the details of these changes.
Some shorter scientific and technical descriptions of the machine are contained in: [Pg 246]
Aiken, Howard H., and Grace M. Hopper, The Automatic Sequence Controlled Calculator (3 parts), Electrical Engineering, vol. 65, nos. 8, 9, and 10, Aug. to Nov. 1946, p. 384 ... (21 pp.).
Bloch, Richard M., Mark I Calculator, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Harvard University Press, 1948, pp. 23-30.
Harrison, Joseph O., Jr., The Preparation of Problems for the Mark I Calculator, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Harvard University Press, 1948, pp. 208-210.
International Business Machines Corporation, IBM Automatic Sequence-Controlled Calculator, Endicott, N. Y.: International Business Machines Corporation, 1945, 6 pp.
Some of the less technical articles regarding the machine are:
Genet, N., Got a Problem? Harvard’s Amazing New Mathematical Robot, Scholastic, vol. 45, Sept. 18, 1944, p. 35.
Torrey, V., Robot Mathematician Knows All the Answers, Popular Science, vol. 145, Oct. 1944, pp. 86-89....
Anonymous, Giant New Calculator, Science News Letter, vol. 46, Aug. 12, 1944, p. 111.
Anonymous, Mathematical Robot Presented to Harvard, Time, vol. 44, Aug. 14, 1944, p. 72.
Anonymous, World’s Greatest Machine for Automatic Calculation, Science News Letter, vol. 46, Aug. 19, 1944, p. 123.
Anonymous, Superbrain, Nation’s Business, vol. 32, Sept. 1944, p. 8.
Anonymous, Robot Works Problems Never Before Solved, Popular Mechanics, vol. 82, Oct. 1944, p. 13.
There is as yet no full-scale, published scientific account of the Eniac. At the Ballistic Research Laboratories, Aberdeen, Md., where the machine now is, there are a few copies of some long mimeographed reports on the machine and the way it works. These were prepared by H. H. Goldstine and others when at the Moore School of Electrical Engineering, as a part of the contract under which the machine was constructed for the U. S. Government. It is possible that these reports might be consulted on request by serious students. [Pg 247]
Some scientific descriptions of the machine and its properties are:
Burks, Arthur W., Electronic Computing Circuits of the ENIAC, Proceedings of the Institute of Radio Engineers, vol. 35, no. 8, Aug. 1947, pp. 756-767.
Clippinger, R. F., A Logical Coding System Applied to the Eniac, B. R. L. Report No. 673, Aberdeen, Md.: Ballistic Research Laboratories, Sept. 29, 1948, 41 pp.
Eckert, J. Presper, Jr., John W. Mauchly, Herman H. Goldstine, and J. G. Brainerd, Description of the ENIAC and Comments on Electronic Digital Computing Machines, Applied Mathematics Panel Report 171.2R, Washington, D. C.: National Defense Research Committee, Nov. 1945, 78 pp.
Goldstine, Herman H., and Adele Goldstine, The Electronic Numerical Integrator and Computer (ENIAC), Mathematical Tables and Other Aids to Computation, vol. 2, no. 15, July 1946, pp. 97-110.
Hartree, D. R., The ENIAC, an Electronic Computing Machine, Nature, vol. 158, Oct. 12, 1946, pp. 500-506.
Hartree, D. R., Calculating Machines: Recent and Prospective Developments and Their Impact on Mathematical Physics, Cambridge, England: The University Press, 1947, 40 pp. (Pages 14 to 27 are devoted to the Eniac.)
Tabor, Lewis P., Brief Description and Operating Characteristics of the ENIAC, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Harvard University Press, 1948, pp. 31-39.
Some of the less technical articles on Eniac are:
Rose, A., Lightning Strikes Mathematics: ENIAC, Popular Science, vol. 148, Apr. 1946, pp. 83-86.
Anonymous, Robot Calculator: ENIAC, All Electronic Device, Business Week, Feb. 16, 1946, p. 50 ...
Anonymous, Answers by ENY: Electronic Numerical Integrator and Computer, ENIAC, Newsweek, vol. 27, Feb. 18, 1946, p. 76.
Anonymous, Adds in ¹/₅₀₀₀ Second: Electronic Computing Machine at the University of Pennsylvania, Science News Letter, vol. 49, Feb. 23, 1946, p. 113 ...
Anonymous, ENIAC: at the University of Pennsylvania, Time, vol. 47, Feb. 25, 1946, p. 90.
Anonymous, It Thinks with Electrons; the ENIAC, Popular Mechanics, vol. 85, June 1946, p. 139.
Anonymous, Electronic Calculator: ENIAC, Scientific American, vol. 174, June 1946, p. 248.
As yet no full-scale scientific report is available on the Bell Laboratories general-purpose relay computers that went to Aberdeen and Langley Field. However, there is some information about these and other Bell Laboratories relay computing machines in the following articles: [Pg 248]
Alt, Franz L., A Bell Telephone Laboratories’ Computing Machine (two parts), Mathematical Tables and Other Aids to Computation, vol. 3, no. 21, Jan. 1948, pp. 1-13, and vol. 3, no. 22, Apr. 1948, pp. 69-84.
Cesareo, O., The Relay Interpolator, Bell Laboratories Record, vol. 24, no. 12, Dec. 1946, pp. 457-460.
Juley, Joseph, The Ballistic Computer, Bell Laboratories Record, vol. 25, no. 1, Jan. 1947, pp. 5-9.
Williams, Samuel B., A Relay Computer for General Application, Bell Laboratories Record, vol. 25, no. 2, Feb. 1947, pp. 49-54.
Williams, Samuel B., Bell Telephone Laboratories’ Relay Computing System, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Harvard University Press, 1948, pp. 40-68.
Anonymous, Complex Computer Demonstrated, Bell Laboratories Record, vol. 19, no. 2, Oct. 1940, pp. v-vi.
Anonymous, Computer Mark 22 Mod. 0: Development and Description, Navord Report No. 178-45, Washington, D. C.: Navy Department, Dec. 6, 1945, 225 pp.
Anonymous, Relay Computer for the Army, Bell Laboratories Record, vol. 26, no. 5, May 1948, pp. 208-209.
As yet there are no published references on the Kalin-Burkhart Logical-Truth Calculator.
Some books covering a good deal of mathematical logic are:
Quine, W. V., Mathematical Logic, New York: W. W. Norton & Co., 1940, 348 pp.
Reichenbach, Hans, Elements of Symbolic Logic, New York: The Macmillan Co., 1947, 444 pp.
Tarski, Alfred, Introduction to Logic, New York: Oxford University Press, 1941, 239 pp.
Woodger, J. H., The Axiomatic Method in Biology, Cambridge, England: The University Press, 1937, 174 pp.
Chapter 2, pp. 18-52, is an excellent and understandable summary of the concepts of mathematical logic.
Several papers on the application of mathematical logic to the analysis of practical situations are:
Berkeley, Edmund C., Boolean Algebra (The Technique for Manipulating “And,” “Or,” “Not,” and Conditions) and Applications to Insurance, Record of the American Institute of Actuaries, vol. 26, Oct. 1937, pp. 373-414.
Berkeley, Edmund C., Conditions Affecting the Application of Symbolic Logic, Journal of Symbolic Logic, vol. 7, no. 4, Dec. 1942, pp. 160-168.
Shannon, Claude E., A Symbolic Analysis of Relay and Switching Circuits, Transactions of the American Institute of Electrical Engineers, vol. 57, 1938, pp. 713-723.
This paper has had a good deal of influence here and there on the development of electric circuits using relays. [Pg 249]
The following report discusses the solution of some problems of mathematical logic by means of a large-scale digital calculator:
Tarski, Alfred, A Decision Method for Elementary Algebra and Geometry, Report R-109, California: Rand Corporation, Aug. 1, 1948, 60 pp.
The Aiken Mark II Relay Calculator
The Computation Laboratory of Harvard University finished during 1947 a second large relay calculator, called the Aiken Mark II Relay Calculator. This machine is alluded to briefly at the end of Chapter 10 and is described more fully in the following:
Campbell, Robert V. D., Mark II Calculator, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 69-79.
Freeland, Stephen L., Inside the Biggest Man-Made Brain, Popular Science, May 1947, pp. 95-100.
Miller, Frederick G., Application of Printing Telegraph Equipment to Large-Scale Calculating Machinery, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 213-222.
The Edsac
The Edsac is a machine under construction in England.
Wilkes, M. V., The Design of a Practical High-Speed Computing Machine: the EDSAC, Proceedings of the Royal Society, series A, vol. 195, 1948, pp. 274-279.
Wilkes, M. V., and W. Renwick, An Ultrasonic Memory Unit for the EDSAC, Electronic Engineering, vol. 20, no. 245, July 1948, pp. 208-213.
The Edvac
The Edvac is a machine under construction at the Moore School of Electrical Engineering, Philadelphia.
Koons, Florence, and Samuel Lubkin, Conversion of Numbers from Decimal to Binary Form in the EDVAC, Mathematical Tables and Other Aids to Computation, vol. 3, no. 26, Apr. 1949, pp. 427-431.
Anonymous, EDVAC Replaces ENIAC, The Pennsylvania Gazette, Philadelphia: University of Pennsylvania, vol. 45, no. 8, Apr. 1947, pp. 9-10.
The IBM Selective-Sequence Electronic Calculator
The IBM Selective-Sequence Electronic Calculator was finished and announced in January 1948, and is alluded to briefly at the end of Chapter 10. More information about this machine is in the following references: [Pg 250]
Eckert, W. J., Electrons and Computation, The Scientific Monthly, vol. 67, no. 5, Nov. 1948, pp. 315-323.
International Business Machines Corporation, IBM Selective-Sequence Electronic Calculator, New York: International Business Machines Corporation (form no. 52-3927-0), 1948, 16 pp.
The Raytheon Computer
The Raytheon Computer is a machine under construction at the Raytheon Manufacturing Co., Waltham, Mass.
Bloch, R. M., R. V. D. Campbell, and M. Ellis, The Logical Design of the Raytheon Computer, Mathematical Tables and Other Aids to Computation, vol. 3, no. 24, Oct. 1948, pp. 286-295.
Bloch, R. M., R. V. D. Campbell, and M. Ellis, General Design Considerations for the Raytheon Computer, Mathematical Tables and Other Aids to Computation, vol. 3, no. 24, Oct. 1948, pp. 317-323.
A “System of Electric Remote-Control Accounting”
During the 1930’s a system using connected punch-card machinery was experimented with in a department store in Pittsburgh. The purpose of the system was automatic accounting and analysis of sales. This system is described in:
Woodruff, L. F., A System of Electric Remote-Control Accounting, Transactions of the American Institute of Electrical Engineers, vol. 57, Feb. 1938, pp. 78-87.
The Univac
The Univac is a machine under construction at the Eckert-Mauchly Computer Corporation, Philadelphia. A similar but smaller digital computer called the Binac is also being developed.
Eckert-Mauchly Computer Corporation, The Univac System, Philadelphia: Eckert-Mauchly Computer Corp., 1948, 8 pp.
Electronic Control Co. (now Eckert-Mauchly Computer Corp.), A Tentative Instruction Code for a Statistical Edvac, Philadelphia: Electronic Control Co. (now Eckert-Mauchly Computer Corp.), May 7, 1947, 19 pp.
Snyder, Frances E., and Hubert M. Livingston, Coding of a Laplace Boundary Value Problem for the UNIVAC, Mathematical Tables and Other Aids to Computation, vol. 3, no. 25, Jan. 1949, pp. 341-350.
The Zuse Computer
The Zuse Computer is a small digital computer constructed in Germany.
Lyndon, Roger C., The Zuse Computer, Mathematical Tables and Other Aids to Computation, vol. 2, no. 20, Oct. 1947, pp. 355-359.
[Pg 251]
Following are a number of references on various aspects of the design of digital computing machines:
Organization
Burks, Arthur W., Super-Electronic Computing Machine, Electronic Industries, vol. 5, no. 7, July 1946, p. 62.
Burks, Arthur W., Herman H. Goldstine and John von Neumann, Preliminary Discussion of the Logical Design of an Electronic Computing Instrument, Princeton, N. J.: Institute for Advanced Study, 2nd edition, Sept. 1947, 42 pp.
Eckert, J. Presper, Jr., John W. Mauchly, and J. R. Weiner, An Octal System Automatic Computer, Electrical Engineering, vol. 68, no. 4, Apr. 1949, p. 335.
Forrester, Jay W., Warren S. Loud, Robert R. Everett, and David R. Brown, Lectures by Project Whirlwind Staff on Electronic Digital Computation, Cambridge, Mass.: Massachusetts Institute of Technology, Servo-mechanisms Laboratory, Mar. and Apr. 1947, 149 pp.
Lubkin, Samuel, Decimal Point Location in Computing Machines, Mathematical Tables and Other Aids to Computation, vol. 3, no. 21, Jan. 1948, pp. 44-50.
Patterson, George W., editor, and others, Theory and Techniques for Design of Electronic Digital Computers (subtitle: Lectures Given at the Moore School 8 July 1946-31 August 1946), Philadelphia: The University of Pennsylvania, Moore School of Electrical Engineering, vol. 1, lectures 1-10, Sept. 10, 1947, 161 pp.; vol. 2, lectures 11-21, Nov. 1, 1947, 173 pp.; vol. 3 and 4 in preparation.
Stibitz, George R., Relay Computers, Applied Mathematics Panel Report 171.1R, Washington, D. C.: National Defense Research Council, Feb. 1945, 83 pp.
Stibitz, George R., Should Automatic Computers be Large or Small? Mathematical Tables and Other Aids to Computation, vol. 2, no. 20, Oct. 1947, pp. 362-364.
Stibitz, George R., The Organization of Large-Scale Calculating Machinery, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 91-100.
Stibitz, George R., A New Class of Computing Aids, Mathematical Tables and Other Aids to Computation, vol. 3, no. 23, July 1948, pp. 217-221.
Input and Output Devices
Alexander, Samuel N., Input and Output Devices for Electronic Digital Calculating Machinery, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 248-253. [Pg 252]
Fuller, Harrison W., The Numeroscope, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 238-247.
O’neal, R. D., Photographic Methods for Handling Input and Output Data, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 260-266.
Tyler, Arthur W., Optical and Photographic Storage Techniques, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 146-150.
Zworykin, V. K., L. E. Flory, and W. S. Pike, Letter-Reading Machine, Electronics, vol. 22, no. 6, June 1949, pp. 80-86.
Anonymous, Letter-Printing Cathode-Ray Tube, Electronics, vol. 22, no. 6, June 1949, pp. 160-162.
Storage Devices
Brillouin, Leon N., Electromagnetic Delay Lines, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 110-124.
Forrester, Jay W., High-Speed Electrostatic Storage, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 125-129.
Haeff, Andrew V., The Memory Tube and its Application to Electronic Computation, Mathematical Tables and Other Aids to Computation, vol. 3, no. 24, Oct. 1948, pp. 281-286.
Kornei, Otto, Survey of Magnetic Recording, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 223-237.
Moore, Benjamin L., Magnetic and Phosphor Coated Discs, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 130-132.
Rajchman, Jan A., The Selectron—A Tube for Selective Electrostatic Storage, Mathematical Tables and Other Aids to Computation, vol. 2, no. 20, Oct. 1947, pp. 359-361 and frontispiece.
Sharpless, T. Kite, Mercury Delay Lines as a Memory Unit, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 103-109.
Sheppard, C. Bradford, Transfer Between External and Internal Memory, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 267-273.
Programming or Coding
Everett, Robert R., Digital Computing Machine Logic (memorandum M-63), Cambridge, Mass.: Massachusetts Institute of Technology, Servo-mechanisms Laboratory, Mar. 19, 1947, 48 pp. [Pg 253]
Goldstine, Herman H., and John von Neumann, Planning and Coding of Problems for an Electronic Computing Instrument, Princeton, N. J.: Institute for Advanced Study, 1947, 69 pp.
Goldstine, Herman H., and John von Neumann, Planning and Coding of Problems for an Electronic Computing Instrument, Princeton, N. J.: Institute for Advanced Study, part 2, vol. 3, 1948, 23 pp.
Mauchly, John W., Preparation of Problems for Edvac-Type Machines, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 203-207.
Many of the following articles are nontechnical and contain much interesting information about machines that think:
Alt, Franz L., New High-Speed Computing Devices, The American Statistician, vol. 1, no. 1, Aug. 1947, pp. 14-15.
Bush, Vannevar, As We May Think, Atlantic Monthly, July 1945, pp. 101-108.
Condon, Edward U., The Electronic Brain Means a Better Future for You (broadcast), Columbia Broadcasting System, Jan. 4, 1948.
Davis, Harry M., Mathematical Machines, Scientific American, vol. 180, no. 4, Apr. 1949, pp. 29-39.
Lagemann, John K., It All Adds Up, Collier’s Magazine, May 31, 1947, pp. 22-23 ...
Locke, E. L., Modern Calculators, Astounding Science Fiction, vol. 52, no. 5, Jan. 1949, pp. 87-106.
MacLaughlan, Lorne, Electrical Mathematicians, Astounding Science Fiction, vol. 53, no. 3, May 1949, pp. 93-108.
Mann, Martin, Want to Buy a Brain? Popular Science, vol. 154, no. 5, May 1949, pp. 148-152.
Newman, James R., Custom-Built Genius, New Republic, June 23, 1947, pp. 14-18.
Pfeiffer, John E., The Machine That Plays Gin Rummy, Science Illustrated, vol. 4, no. 3, Mar. 1949, pp. 46-48 ...
Ridenour, Louis N., Mechanical Brains, Fortune, vol. 39, no. 5, May 1949, pp. 108-118.
Tumbleson, Robert C., Calculating Machines, Federal Science Progress, June 1947, pp. 3-7.
Anonymous, Almost Human, Home Office News, Newark, N. J.: Prudential Insurance Company of America, Feb. 1947, p. 8.
Some of the problems that mechanical brains can solve, some of the methods for controlling them to solve problems, and some of the [Pg 254] implications of mechanical brains for future problems are covered in the following references:
Solving Problems
Berkeley, Edmund C., Electronic Machinery for Handling Information, and its Uses in Insurance, Transactions of the Actuarial Society of America, vol. 48, May 1947, pp. 36-52.
Berkeley, Edmund C., Electronic Sequence Controlled Calculating Machinery and Applications in Insurance, Proceedings of 1947 Annual Conference, Life Office Management Association, New York: Life Office Management Association, 1947, pp. 116-129.
Curry, Haskell B., and Willa A. Wyatt, A Study of Inverse Interpolation of the Eniac, B. R. L. Report No. 615, Aberdeen, Md.: Ballistic Research Laboratories, Aug. 19, 1946, 100 pp.
Harrison, Joseph O., Jr., and Helen Malone, Piecewise Polynomial Approximation for Large-Scale Digital Calculators, Mathematical Tables and Other Aids to Computation, vol. 3, no. 26, Apr. 1949, pp. 400-407.
Hoffleit, Dorrit, A Comparison of Various Computing Machines Used in Reduction of Doppler Observations, Mathematical Tables and Other Aids to Computation, vol. 3, no. 25, Jan. 1949, pp. 373-377.
Leontief, Wassily W., Computational Problems Arising in Connection with Economic Analysis of Interindustrial Relationships, Proceedings of a Symposium on Large-Scale Digital Calculating Machinery, Cambridge, Mass.: Harvard University Press, 1948, pp. 169-175.
Lotkin, Max, Inversion on the Eniac Using Osculatory Interpolation, B. R. L. Report No. 632, Aberdeen, Md.: Ballistic Research Laboratories, July 15, 1947, 42 pp.
Lowan, Arnold N., The Computation Laboratory of the National Bureau of Standards, Scripta Mathematica, vol. 15, no. 1, Mar. 1949, pp. 33-63.
Matz, Adolph, Electronics in Accounting, Accounting Review, vol. 21, no. 4, Oct. 1946, pp. 371-379.
McPherson, James L., Applications of High-Speed Computing Machines to Statistical Work, Mathematical Tables and Other Aids to Computation, vol. 3, no. 22, Apr. 1948, pp. 121-126.
Mitchell, Herbert F., Jr., Inversion of a Matrix of Order 38, Mathematical Tables and Other Aids to Computation, vol. 3, no. 23, July 1948, pp. 161-166.
Anonymous, Revolutionizing the Office, Business Week, May 28, 1949, no. 1030, pp. 65-72.
Speech
Some of the possibilities of machines dealing with voice and speech are indicated in: [Pg 255]
Dudley, Homer, R. R. Riesz, and S. S. A. Watkins, A Synthetic Speaker, Journal of the Franklin Institute, vol. 227, June 1939, pp. 739-764.
This is an article on the Voder, which is an abbreviation of Voice Operation Demonstrator. The machine was exhibited at the New York World’s Fair, 1939.
Dudley, Homer, The Vocoder, Bell Laboratories Record, vol. 18, no. 4, Dec. 1939, pp. 122-126.
This is a more general type of machine than the Voder. The Vocoder is both an analyzer and synthesizer of human speech.
Potter, Ralph K., George A. Kopp, and Harriet C. Green, Visible Speech, New York: D. Van Nostrand Co., 1947, 441 pp.
Anonymous, Pedro the Voder: A Machine that Talks, Bell Laboratories Record, vol. 17, no. 6, Feb. 1939, pp. 170-171.
Weather
Some of the possibilities of machines dealing with weather information are covered in:
Lagemann, John K., Making Weather to Order, New York Herald Tribune: This Week, Feb. 23, 1947.
Shalett, Sidney, Electronics to Aid Weather Figuring, The New York Times, Jan. 11, 1946.
Zworykin, V. K., Outline of Weather Proposal, Princeton, N. J.: Radio Corporation of America Research Laboratories, Oct. 1945, 11 pp.
Anonymous, Weather Under Control, Fortune, Feb. 1948, pp. 106-111 ...
The Robot Machine
Čapek, Karel, R. U. R. (translated from the Czech by Paul Selver), New York: Doubleday, Page & Co., 1923.
Lagemann, John K., From Piggly Wiggly to Keedoozle, Collier’s Magazine, vol. 122, no. 18, Oct. 30, 1948, pp. 20-21 ...
Leaver, E. W., and J. J. Brown, Machines Without Men, Fortune, vol. 34, no. 5, Nov. 1946, pp. 165 ...
Pease, M. C., Devious Weapon, Astounding Science Fiction, vol. 53, no. 2, Apr. 1949, pp. 34-43.
Shannon, Claude E., Programming a Computer for Playing Chess, Bell Telephone Laboratories, Oct. 8, 1948, 34 pp.
Shelley, Mary W., Frankenstein (in Everyman’s Library, No. 616), New York: E. P. Dutton & Co., last reprinted 1945, 242 pp.
Spilhaus, Athelstan, Let Robot Work for You, The American Magazine, Dec. 1948, p. 47 ...
Anonymous, Another New Product for Robot Salesmen, Modern Industry, vol. 13, no. 2, Feb. 15, 1947.
Anonymous, The Automatic Factory, Fortune, vol. 34, no. 5, Nov. 1946, p. 160 ...
Anonymous, Machines Predict What Happens in Your Plant, Business Week, Sept. 25, 1948, pp. 68-69 ...
[Pg 256]
[Pg 257]
Note: This list of persons mentioned in the text includes names of fictional characters. The subject index, which follows, includes all other names.
[Pg 261]
Notes: Phrases consisting of an adjective and a noun, or of a noun and a noun, are entered in their alphabetical place according to the first word. For example, “electrostatic storage tube” is under e, and “punch card” is under p.
Footnotes:
[1] Copyright 1923 by Doubleday, Page and Co.; all rights reserved; quotations reprinted by permission of Karel Čapek and Samuel French.
[2] The preceding word is the spoken word, not the written one.
[3] The preceding word is the spoken word, not the written one.
[4] The preceding word is the spoken word, not the written one.
[5] The preceding word is the spoken word, not the written one.
Transcriber’s Notes:
The illustrations have been moved so that they do not break up paragraphs and so that they are next to the text they illustrate.
Typographical and punctuation errors have been silently corrected.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBook.