
Anmerkungen zur Transkription
Der vorliegende Text wurde anhand der Buchausgabe von 1919 so weit wie möglich originalgetreu wiedergegeben. Typographische Fehler wurden stillschweigend korrigiert. Ungewöhnliche und heute nicht mehr verwendete Schreibweisen bleiben gegenüber dem Original unverändert; fremdsprachliche Ausdrücke wurden nicht korrigiert.
Der Übersichtlichkeit halber wurden alle Buchanzeigen am Ende des Texts zusammengefasst. Die Fußnoten wurden an das Ende des jeweiligen Abschnitts verschoben.

Aus Natur und Geisteswelt
Sammlung wissenschaftlich-gemeinverständlicher Darstellungen
637. Bändchen
Von
Dr. Kurt Joachim Grau

Verlag von B. G. Teubner in Leipzig und Berlin 1918

Berthold Goldstein
dem toten Freunde
in treuem Gedenken
(Gefallen am 13. Juni 1915 beim Sturmangriff unweit Jaroslau in den Kämpfen zur Befreiung Galiziens)
„Ich bin der Meinung, man täte wohl, daß man die Mathematik, Historie und anderes vor der ausführlichen Logik lernte; denn wie will der die Gedanken wohl ordnen, der noch wenig bedacht? Wenn man aber mit einem Vorrat guter Gedanken versehen, dann kann man sie mustern und abmessen, und mit Hilfe der darin sich zeigenden Ordnung desto besser auf etwas Neues kommen. Es ist hierin wie mit der Sprachkunst, da bin ich auch der Meinung, man solle sich bei Erlernung einer Sprache mehr an die Übung als Grammatik halten; wenn man aber schon ziemlich in der Sprache erfahren, dann dienet die Grammatik, darin höher zu steigen.“
G. W. Leibniz (Brief an
Gabriel Wagner, 1696.)
[S. v]
Der vorliegende „Grundriß der Logik“ erwuchs im wesentlichen aus pädagogischen Motiven. Dem Schüler und Studenten, ja dem philosophisch Interessierten überhaupt, einen kurzen, übersichtlichen Leitfaden in die Hand zu geben, der ihn über die Hauptfragen der Logik orientiert, über ihre verschiedenen Lösungsversuche und den gegenwärtigen Stand der Probleme, der ihm zugleich den Weg weist zu weiteren und tieferen Studien auf diesem nützlichen Gebiete menschlichen Wissens, hat dem Verfasser als Ziel und Aufgabe vorgeschwebt.
Daraus ergab sich, daß manches unerörtert bleiben mußte, was dem Zweck dieser als Einführung gedachten Arbeit widersprochen und auch sonst allzusehr ins Spezielle, ins Polemische sowie in die Grenzgebiete logischer Betrachtung geführt hätte. Der Verfasser hat sich daher durchgehends bemüht, sich in der Darstellung streng an sein vorgeschriebenes Thema zu halten und alles Psychologische, Grammatische und Erkenntnistheoretische nur so weit heranzuziehen, wie es für die eigentliche Aufgabe, die Erörterung der logischen Probleme, unumgänglich notwendig erschien. Daß eine solche Beschränkung nicht immer leicht ist, wird, wer je versucht hat, ein System der Logik abzuhandeln, wohl wissen; nicht minder aber auch, daß die Vorteile strenger Abgrenzung der Wissenschaften gegenüber deren Nachteilen bei weitem überwiegen. Auch sonst standen bei der Abfassung didaktische Gesichtspunkte über den theoretisch-wissenschaftlichen. Der Grundriß sollte nicht so sehr untersuchen wie darstellen; sollte weniger dazu beisteuern, Probleme zu lösen als zu zeigen, wie aus gegebenen Lösungsversuchen neue Probleme entstehen. Die verschiedenen gegenwärtig miteinander streitenden Richtungen der Logik (die formale, metaphysische und erkenntnistheoretische, psychologisierende, mathematische, Inhalts- und Umfangs-, induktive und deduktive Logik) sind, wie ich glaube, in genügender Weise zum Ausdruck gekommen.[S. vi] Eine kritische Stellungnahme innerhalb dieser zum Teil arg auseinandergehenden Strömungen war unvermeidlich, entsprechend dem allgemein anerkannten Grundsatz, daß es nur eine Wahrheit und in wissenschaftlichen Dingen gegenüber dem als unzureichend Erkannten keine Toleranz geben dürfe.
Daß ich mit erläuternden Beispielen im Text nicht gespart habe, wird man mir nicht als eine unnötige Belastung des Bändchens auslegen wollen; haben diese doch (nach der treffenden Bemerkung Drobischs) im Lehrbuch der Logik eine ähnliche Funktion wie die veranschaulichenden Figuren im Lehrbuch der Geometrie.
Der Darstellung ist ein Literaturverzeichnis angehängt, das Fingerzeige zur weiteren Beschäftigung mit logischen Fragen enthält.
Berlin, im Sommer 1917.
Der Verfasser.
[S. vii]
|
Seite
|
|||
| 1. |
Die Stellung der Logik im System der Philosophie
|
||
| 2. |
Über Begriff, Aufgabe und Einteilung der Logik
|
||
| 3. |
Die geschichtlichen Voraussetzungen der neueren Logik
|
||
| 1. |
Psychologische Vorbemerkungen über das Verhältnis von
Sprechen und Denken
|
||
| 2. |
Die Gegenstände des Denkens und die Bedeutung der
Begriffe
|
||
| 3. |
Das Wesen des Begriffes und sein Inhalt
|
||
| 4. |
Der Umfang des Begriffes und sein Verhältnis zum
Inhalt
|
||
| 5. |
Arten und Ordnungsreihen der Begriffe; Kategorien
|
||
| 1. |
Arten und Ordnung der Urteile
|
||
| 2. |
Logische Theorie des Urteils
|
||
| 3. |
Formale und materiale Bedingungen der
Urteilsgültigkeit
|
||
| 4. |
Das Subjektsglied der Urteile und die
Subjekt-unbestimmten Urteile
|
||
| 5. |
Das Prädikatsglied der Urteile und die Arten der
Prädizierungen
|
||
| 6. |
Wesen und Arten der Beurteilungen
|
||
| 7. |
Die zusammengesetzten Urteile (Urteilsverbindungen
und Urteilsgefüge)
|
||
| 8. |
Wesen und Arten der Frage
|
||
| 1. |
Die unmittelbaren Schlüsse oder Folgerungen
|
||
| 2. |
Die Arten der mittelbaren Schlüsse und die
kategorischen Deduktionen
|
||
| 3. |
Hypothetische Deduktionen und Zusammensetzungen
deduktiver Schlüsse
|
||
| 4. |
Logische Theorie des deduktiven Schließens
|
||
| 5. |
Die induktiven Schlüsse und die Theorie der Induktion
|
||
| 6. |
Das Wesen und die logische Bedeutung der
Analogieschlüsse
|
||
| [S. viii] | |||
| 1. |
Unwissenschaftliches und wissenschaftliches Denken
und die Aufgaben der Methodenlehre
|
||
| 2. |
Wissenschaftliche Begriffsbildung und
Begriffsbestimmung
|
||
| 3. |
Das analytische Untersuchungsverfahren
|
||
| 4. |
Das Experiment und die wissenschaftliche Erfindung
als Hilfsmittel der Analyse
|
||
| 5. |
Das synthetische Untersuchungsverfahren (Gesetz,
Theorie, Hypothese)
|
||
| 6. |
Die Klassifikation und das Begriffssystem der
Wissenschaften
|
||
| 1. |
Begriff und Arten des Beweises
|
||
| 2. |
Die Auffindung der Beweisgründe
|
||
| 3. |
Fehler und Unzulänglichkeiten des Beweises
|
||
| 4. |
Fiktionen und Utopien
|
||
|
Literaturnachweise
|
|||
|
Sachregister
|
|||
[S. 1]
Was Philosophie ist, was Philosophie soll, darauf gibt es fast ebenso viele Antworten, wie es Philosophen gegeben hat. Wer die Geschichte der Philosophie aufmerksam durchgeht, von den Tagen der Griechen bis auf die neueste Zeit, der steht wohl staunend vor der bunten Mannigfaltigkeit von Auffassungen, die Wesen und Zweck des philosophischen Denkens im Laufe der Jahrhunderte gefunden hat.
Nur der oberflächliche Betrachter vermag aus dieser Tatsache einen Einwand gegen die Existenzberechtigung der Philosophie herzuleiten. Es sind erfahrungsgemäß nicht die unfruchtbarsten Wissenschaften, die ihr spezielles Untersuchungsgebiet, den ihnen eigenen Standpunkt der Betrachtung und die dazu gehörige Methode erst spät finden; und alle Wege zur wahren Einsicht führen über Irrtümer und Täuschungen.
Dennoch gibt es heutzutage eine Anzahl Forscher, meist Vertreter der Naturwissenschaften, die der Philosophie mit mehr oder minder offen eingestandener Mißachtung gegenüberstehen und ihr den Rang einer Wissenschaft aberkennen wollen. Sehr zu Unrecht! Denn wer so denkt, übersieht ganz und gar die eigentümliche Stellung, welche die Philosophie bisher in der Geschichte der Wissenschaften eingenommen, und die außerordentlichen Leistungen, die sie für Ursprung und Fortschritt der wissenschaftlichen Erkenntnis vollzogen hat. Gerade die Philosophie ist es (die Geschichte bietet dafür die bündigsten Beweise), die fast alle anderen Wissenschaften, insbesondere die von der äußeren Natur, gewissermaßen geboren und an ihrer Mutterbrust großgezogen hat. Zur Zeit des Aristoteles, des größten Forschers des Altertums, gibt es nur eine Wissenschaft, die Philosophie, und alle besonderen Erkenntnisse sind Zweige und Äste dieser einen. Dieselbe Auffassung findet sich der Hauptsache nach auch noch zu Anfang[S. 2] der Blütezeit der neueren Philosophie, im 17. Jahrhundert, bei Bacon, bei Gassendi, Hobbes und Descartes, nur daß hier bereits Wissenschaften wie die Theologie und Mathematik sich zum Teil emanzipiert haben, und die Philosophie selbst sich in einzelne Disziplinen zu sondern beginnt, wie Hobbes z. B. eine „philosophia naturalis“ und „philosophia civilis“ (Natur- und Bürgerphilosophie) unterscheidet, und wenig später in der englischen Philosophie des 18. Jahrhunderts (mit den Bezeichnungen „natural philosophy“ und „moral philosophy“) die Scheidung in die Philosophie des Geistes und der Natur aufkommt. Nennt doch auch selbst Newton sein großes wissenschaftliches Hauptwerk noch „philosophiae naturalis principia mathematica“ (Mathematische Prinzipien der Naturphilosophie, erschienen im Jahre 1687). Das 18. und das 19. Jahrhundert sind die Epochen der Differenzierung der Wissenschaften, d. h. der allmählichen Loslösung der Einzeldisziplinen von ihrem philosophischen Mutterboden, und zugleich Blütezeiten philosophischer Arbeit. Und gerade jetzt, in unseren Jahrzehnten, erleben wir wieder das Schauspiel, daß Wissenschaften, die bereits als Teile philosophischer Erkenntnis eine jahrhundertelange Geschichte aufweisen, nun sie genügende Reife erlangt haben, sich aus dem Schoße der Philosophie entfernen und zu selbständigen Forschungen heranwachsen: die Psychologie und die Ästhetik.
Diese allmähliche fortschreitende Absonderung philosophischer Disziplinen von ihrer Mutterwissenschaft ist nun freilich nicht einer völligen Trennung gleich zu erachten, dergestalt, daß die Philosophie, nachdem sie alle ihre Zweige und Äste zu selbständigen Einzelwissenschaften erhoben hätte, zuletzt selbst gleichsam leer und ohne Gegenstand ausginge. Vielmehr bleibt zwischen der Philosophie und den Einzelforschungen ein eigentümliches Verhältnis derart bestehen, daß die Philosophie die Einzelwissenschaften zwar nicht ihrem Inhalt, wohl aber ihrer Form nach als Objekte der Forschung beibehält. Die Philosophie als Mutter aller wissenschaftlichen Erkenntnis ist in ihrem theoretischen Teil zugleich Wissenschaft aller wissenschaftlichen Erkenntnis. Ihre Gegenstände sind das wissenschaftliche Denken und Erkennen, das wissenschaftliche Untersuchungs- und Begründungsverfahren schlechthin, kurzum das geistige Instrument, dessen sich der Forscher in seinem Wirken bedient, das er selbst aber als gegeben hinnimmt und zumeist nach Bestand und Voraussetzungen ununtersucht läßt.
[S. 3]
Alle Wissenschaften bedürfen, um zu Resultaten zu kommen, als Mittel dazu des Denkens und des Erkennens. Ist die Philosophie Wissenschaft der wissenschaftlichen Verfahrungsweisen, so ist sie damit Wissenschaft vom Denken und Erkennen. Nun aber sind das Erkennen und Denken bereits Gegenstände einer anderen Wissenschaft, der Psychologie, die diese wie alle anderen psychischen Vorgänge nach ihrem Bestande und Verlaufe analysiert und ihre gesetzlichen Beziehungen untereinander sowie zu den physiologischen Korrelaten festzustellen sucht. Wozu bedarf es außerdem noch einer Philosophie, die das Denken und Erkennen zum Gegenstande besonderer Forschung macht?
Dieser naheliegende Einwand löst sich sofort, wenn wir den Begriff der Philosophie auf eine genauere Formel bringen, als es bisher geschehen ist. Philosophie ist (nach ihrem theoretischen Teile betrachtet) nicht schlechthin die Wissenschaft vom Erkennen und Denken. Sie untersucht diese nicht wie die Psychologie auf die tatsächlichen Elemente ihres Aufbaues; sie ist vielmehr die Wissenschaft von den im Denken und Erkennen immanent liegenden allgemeinen Regeln und Gesetzen, die allem speziellen Denken und Erkennen Gesetz und Regel vorschreiben. Diese allgemeinen Gesetze und Regeln bleiben in den sogenannten positiven Einzelwissenschaften ununtersucht; sie gelten als selbstverständliche und darum unerörtert gelassene Voraussetzungen aller Wissenschaft. Solcher Voraussetzungen gibt es zweierlei Art: Voraussetzungen des Erkennens und des Denkens. Voraussetzungen des Erkennens sind z. B. die Annahme einer vom Wahrnehmen unabhängig-realen Welt von Körpern, die Annahme der objektiven Realität und Dreidimensionalität des Raumes, der Gültigkeit der Anwendung von Zeit, Zahl und Kausalbegriff auf die als real vorausgesetzte Körperwelt u. a. m.; wir nennen diese mit B. Erdmann (Logik I2, S. 18) materiale Voraussetzungen der Wissenschaft. Voraussetzungen des Denkens sind die Annahme der absoluten Allgemeingültigkeit der Formen unseres Urteilens und Schließens und deren ungeprüfte Anwendung in den Methoden der Wissenschaften; wir nennen diese — im Gegensatz zu den materialen — formale Voraussetzungen der Wissenschaft. Entsprechend dieser Unterscheidung zerfällt die Philosophie (wenn wir, wie es hier geschehen ist, sie nur in ihrem theoretischen Teile betrachten) in zwei Hauptdisziplinen: sie ist, wo sie die materialen Voraussetzungen untersucht, Wissenschaft[S. 4] von der Erkenntnis oder Erkenntnislehre; wo sie die formalen Voraussetzungen prüft, Wissenschaft vom Denken oder Logik.
Betrachten wir das an die Funktionen der Sprache geknüpfte Denken nicht nach seinem Ursprunge und Verlaufe, sondern nach seinen gedanklichen Ergebnissen, den Urteilen und Fragen, so können wir an allem Gedachten unterscheiden zwischen der Materie (Stoff, Inhalt), welche gedacht, und der Form, in der das Gedachte uns zum geistigen Eigentum wird. Um das an einem Beispiel zu erläutern: Nehmen wir die Urteile: „Friedrich der Große regierte 6 Jahre länger als Maria Theresia; Das spezifische Gewicht des Wismuts ist in flüssigem Aggregatzustande höher als in festem; Die Lichtstrahlen pflanzen sich in der Luft im allgemeinen ungefähr eine Million mal so schnell fort wie die Schallwellen“, so ist leicht zu ersehen, daß diese drei zwar einen verschiedenen Inhalt, aber die gleiche Form haben. Sie sind sogenannte „quantitative Relationsurteile“, deren logisches Prädikat (P) das logische Subjekt (S) in ein bestimmtes Größen- oder Maßverhältnis zu einem im Prädikat bezeichneten Vergleichs- oder Beziehungsobjekt rückt. Und doch ist das eine dem Bestande der Geschichte, das andere dem Bestande der Chemie und das dritte dem der Physik entnommen. Geringe Überlegung lehrt demnach, daß das Denken zwar über unendlich viele verschiedene Stoffe, aber nur über relativ wenige Formen verfügt, in denen es diese gedanklich fixiert. Es dürfte daher ganz treffend sein, das Denken etwa mit einer Art Münze zu vergleichen, in der die verschiedensten Metalle in verhältnismäßig wenigen festen Formen geprägt werden.
Wäre die Logik schlechthin die Wissenschaft vom Denken, untersuchte sie also sowohl den Inhalt des Denkens wie dessen Formen, so müßte sie offenbar dem Inbegriff aller Wissenschaften identisch sein. Mit anderen Worten: sie wäre eine Art Universalwissenschaft, und der Logiker müßte, wollte er zu Werke gehen, vorerst die Ergebnisse aller bisherigen wissenschaftlichen Arbeit beherrschen. Damit aber wäre sie eine überflüssige und fruchtlose Betätigung, abgesehen davon, daß sie in diesem Sinne ein für den Einzelmenschen unmögliches Unterfangen darstellte. Gegenstand der logischen Untersuchung ist nach dem Gesagten aber nicht der Inhalt des Denkens, sondern dessen[S. 5] Form. Die Logik ist mithin die Wissenschaft von den Formen des Denkens, also eine formale Wissenschaft. Das ist sie aber nicht in dem Sinne, in dem Kant sie definierte, daß sie nämlich von allem und jedem Inhalt des Denkens schlechthin abstrahiere. Form und Materie sind nur in bedingtem Maße voneinander zu trennen; denn wie die Form nicht ohne Inhalt, so ist der Inhalt nicht ohne Form möglich. Beide bedingen und ergänzen einander dergestalt, daß der Inhalt sich die Form schafft, und die Form wiederum dem Inhalt das logische Gepräge gibt. Die Logik kann also — obschon eine formale Wissenschaft — nur von allem besonderen und bestimmten Inhalte abstrahieren, nicht aber vom Inhalte des Denkens überhaupt und im allgemeinen (vgl. Drobisch, Neue Darstellung der Logik, 1863, § 5). — Die Formen des Denkens sind es, die diesem — gegenüber seinen mannigfachen Materien — einen festen, gesetzlichen Charakter verleihen. Sie sind das Stetige im Flusse; der ruhende Punkt in der Erscheinungen Flucht; das Beharrende, Bleibende und Unveränderliche des Denkprozesses gegenüber dem wechselvollen Inhalte unserer Gedanken. Sie bilden mithin Gesetz und Regel des Denkens. Ist der Inhalt dasjenige, was wir denken, so die Form das, wie wir denken. Und diese Formen festzustellen, in den einfachsten wie in den kompliziertesten Denkprozessen, ihre Beziehungen zueinander, die Bedingungen ihrer Gültigkeit sowie ihre Bedeutung und ihren Wert speziell für die wissenschaftliche Forschung — das ist die Aufgabe, die die logische Untersuchung des Denkens zu leisten hat. Danach ist die Logik — als die Wissenschaft von den Formen des Denkens — zugleich die Wissenschaft von den Gesetzen des Denkens.
Mit dem Gesagten ist die Begriffsbestimmung der Logik noch nicht erschöpft. Als Wissenschaft von den Formen (und dementsprechend von den Gesetzen) des Denkens ist die Logik eine Disziplin, welche ihren Gegenstand in der Erfahrung vorfindet, ihn dort analysiert und auf Grund der Ergebnisse dieser Analyse durch synthetisches Fortschreiten zu den von ihr gesuchten Resultaten gelangt. Mit der Erreichung dieses Zieles sind die Aufgaben, die der Logik gestellt sind, erfüllt. Diese Auffassung widerspricht nun einer weitverbreiteten Annahme, der zufolge die Logik nicht bloß eine feststellende, sondern vielmehr eine lehrende (normative) Disziplin sei. Nach dieser bestehe ihre Aufgabe darin, dem ungeübten Denker wahres und falsches Denken zum Bewußtsein[S. 6] zu bringen und ihn darüber zu unterrichten, wie man beides unterscheide und zu sicheren Resultaten im Denken gelange. Vornehmlich die deutschen Logiker des 18. Jahrhunderts, (so Christian Wolff und seine Schüler), haben diese Definition mit aller Entschiedenheit zum Ausdruck gebracht und demzufolge die Logik als eine „Vernunft-lehre“, „Vernunft-kunst“ oder auch geradezu als „Kunst-lehre“ (Schule) des Denkens bezeichnet. — In dieser Aufgabebestimmung steckt gewiß insofern ein richtiger Kern, als die Logik — mehr vielleicht denn andere Wissenschaften — die Eigenschaft hat, die Fähigkeit des Denkens bei dem, der sich mit ihr beschäftigt, zu schärfen. Ob sie indessen in dieser Hinsicht mehr zu leisten vermag als die Mathematik, ist zum mindesten sehr zweifelhaft. Und es wird gewiß keinem einfallen, etwa die Mathematik wegen ihrer das formale Denken fördernden Wirkungen eine normative Wissenschaft zu nennen. Der normative Charakter der Logik wird damit im Prinzip zugestanden; aber dieses Zugeständnis geht nicht weiter als bis zu der Behauptung, daß die Logik ihrem Wesen nach zunächst eine feststellende Wissenschaft sei; und daß ihre Eigenschaft, darüber hinaus noch die Fähigkeit des Denkens zu stärken, nicht die Erfüllung einer ihrer unmittelbaren Aufgaben, sondern nur einen aus ihrem Wesen resultierenden Nebenerfolg darstellt.
Um Begriff und Aufgabe der Logik noch genauer zu kennzeichnen, ist es zweckmäßig, ihr Verhältnis zur Erkenntnistheorie, zur Psychologie des Denkens und zur Grammatik kurz zu beleuchten. Die Erkenntnistheorie untersucht, wie oben gesagt, die allgemeinen, von den Einzelwissenschaften ununtersucht gelassenen Voraussetzungen des Erkennens, ihrem Wesen nach die materialen; die Logik die von den Wissenschaften ungeprüften Voraussetzungen des Denkens, ihrem Wesen nach die formalen. Was sind nun Erkennen und Denken, und wie verhalten sie sich zueinander? — „Erkennen“ bezeichnet im logischen Sinne den Inbegriff derjenigen Vorgänge, durch die ein Bestandteil des Bewußtseins als Gegenstand erfaßt wird. Einen Bewußtseinsbestandteil als Gegenstand erfassen heißt aber: ihn nach seinem wesentlichen Inhalt bestimmen als das, was er ist, und ihn als von seinem Vorgestelltwerden unabhängig wirklich voraussetzen. Nun ist ersichtlich, daß sowohl das „nach seinem Inhalt bestimmen“ wie das „als unabhängig wirklich voraussetzen“ Funktionen sind, die Urteilscharakter tragen. Da ferner alles Denken ein Urteilen ist, und danach das Erkennen selbst eine — und zwar komplizierte — Form des Denkens bildet, so sind die Voraussetzungen des Denkens (die formalen) auch zugleich mittelbare Voraussetzungen des Erkennens, die des Erkennens (die materialen) aber nicht solche des Denkens. Demzufolge ist die Logik als Grundwissenschaft der Philosophie zu bezeichnen, die der Erkenntnistheorie ihrem Wesen nach notwendig voranzugehen hat. (Über die Probleme[S. 7] der Erkenntnistheorie vergl. man August Messer, Einführung in die Erkenntnistheorie, Leipzig 1909.)
Die Psychologie des Denkens hat — wie bereits oben angedeutet — die Aufgabe, den Ursprung und Verlauf des Denkens nach seinen grundlegenden Elementen, deren Verhältnis zum Vorstellen, Sprechen und Fühlen sowie zu den physiologischen Korrelaten im Zentralnervensystem gesetzlich zu bestimmen. Sie betrachtet die Produkte des Denkens, also das Gedachte, nur insoweit, als sie festzustellen hat, in welcher Gestalt des Erlebens uns dieses zu Bewußtsein kommt, und in bezug auf etwaige emotionale oder physiologische Begleiterscheinungen. Eine abstrahierende Scheidung zwischen Form und Inhalt des Urteils kennt die Psychologie nicht: sie nimmt das Urteil als Ganzes und untersucht es als seelischen Vorgang auf seine Entstehung, auf seinen Bewußtseinsbestand, seine Korrelate, nicht aber auf seine Form im Unterschied von seinem Inhalt. Die Psychologie des Denkens fragt: Was geht in uns vor, wenn wir denken?; die Logik: wie, d. h. in welchen Formen denken wir? — Damit ist das Wesen der Psychologie des Denkens und der Logik genügend unterschieden; aber es fragt sich noch, wie sich der Logiker zu seiner Schwesterwissenschaft, der Psychologie des Denkens, zu stellen habe. Der Logiker ist kein Psychologiefeind. Je klarer und bewußter er die Aufgaben seiner Wissenschaft von denen der Psychologie zu scheiden weiß, mit um so größerem Nutzen für die eigene Forschung wird er sich der Psychologie hingeben und sich von ihr belehren lassen. Nur eine Vermengung muß beiden Wissenschaften Schaden bringen. Reinlich auseinandergehalten befruchten sie einander gegenseitig und fördern eine der anderen Bestand. Namentlich für den Logiker ist die Kenntnis der psychologischen Analyse des Denkens und Sprechens, speziell des Vorgangs der Begriffsbildung, der Abstraktion, der Urteils- und Schlußfunktionen ungemein wichtig, wenngleich es nicht unbedingt erforderlich ist, daß jeder Darstellung der Logik ein Abriß der Psychologie des Denkens vorhergeht. Andererseits ist auch die gänzliche Ausschaltung alles Psychologischen aus der Logik unzweckmäßig, weil die Erörterung psychologischer Tatsachen — als solche streng geschieden von den eigentlich logischen Fragen — das Verständnis der logischen Probleme in mancher Hinsicht fördert und hebt.
Das Verhältnis der Logik zur Grammatik kann hier nur im allgemeinen behandelt werden, da für eine genauere Betrachtung eine eingehendere Erörterung über das Verhältnis von Sprechen und Denken Voraussetzung wäre. Die Grammatik kann definiert werden als die Wissenschaft vom elementaren Aufbau der Sprachen. Als solche bildet sie den systematischen Teil der allgemeinen Sprachwissenschaft; sie untersucht die Laute, die Stämme und Wurzeln, die Flexionen, die Syntax der verschiedenen Sprachen auf ihren Bestand und vergleicht sie miteinander innerhalb eines und desselben Sprachstammes und mit anderen Sprachstämmen (allgemeine und vergleichende Grammatik). Demzufolge gibt es ebenso viele verschiedene Grammatiken wie es Sprachen gibt: eine Grammatik des Angelsächsischen ebenso wie eine des Althochdeutschen, des Hebräischen wie des Chinesischen. Daraus erhellt der Unterschied zwischen der Logik und der Grammatik: es gibt viele Grammatiken, ebenso viele wie Sprachen, aber nur eine Logik. In und vermittels welcher Sprache man auch denken und seine Gedanken zum Ausdruck bringen mag, die Formen des Denkens bleiben dieselben. Es ist für den logischen Aufbau eines[S. 8] Urteils gleich, ob man es in einer germanischen, romanischen, slawischen oder etwa gar in einer der mongolischen Sprachen formuliert, vorausgesetzt, daß in allen diesen Formulierungen derselbe Sinn zum Ausdruck gelangt. Das sprachliche Gewand des Denkens kann mithin wechseln, aber das Denken und seine Form selbst bleibt sich gleich. Damit ist erwiesen, daß die Logik nicht nur gänzlich verschieden, sondern auch gänzlich unabhängig von der Grammatik ist, wenngleich auch hier anregende Wechselbeziehungen zwischen beiden als in reichem Maße vorhanden zugegeben werden sollen.
Die übliche Einteilung der Logik richtet sich nach ihrem Begriff und ihrer Aufgabe. Als allgemeine Wissenschaft von den Formen des Denkens — des unwissenschaftlichen sowohl wie des wissenschaftlichen — ist sie eine Elementarlehre des Denkens überhaupt. Als solche untersucht sie dieses auf seine einfachsten formalen Elemente, als die sich ihr — nach einer zuerst von Petrus Ramus aufgestellten Einteilung — die verschiedenen Arten der Begriffe, Urteile und Schlußweisen ergeben. Als spezielle Wissenschaft von den methodischen Formen des wissenschaftlichen Denkens ist sie eine Methodenlehre der Wissenschaft; als solche untersucht sie, welche Anwendung und Bedeutung die in der Elementarlehre aufgezeigten Elemente in dem Verfahren der Wissenschaft haben, und analysiert den formalen Aufbau der wissenschaftlichen Methodik auf seine grundlegenden Faktoren, als die sie die verschiedenen Formen des wissenschaftlichen Untersuchungs- und des wissenschaftlichen Beweisverfahrens voneinander unterscheidet.
Die Logik als Wissenschaft ist eine Schöpfung des griechischen Geistes. Angelegt in den Spitzfindigkeiten des genialen Zenon aus Elea (um 500 v. Chr.) und in den dialektischen Streitigkeiten der Sophisten, die zuletzt eine allgemeingültige Wahrheit überhaupt leugnen und damit die Frage nach dem Wesen einer formell-richtigen Beweisführung im Gegensatz zu den beliebten Trug- und Fangschlüssen ihrer Zeit zum Problem erheben; vorbereitet ferner durch die Sokratisch-Platonischen Gespräche über das Wesen des Begriffs (λόγος), der Begriffsbestimmung und der Einteilung eines Begriffes, über das Wesen der Wissenschaft (ἐπιστήμη), das Verhältnis von Denken und Empfinden (νοεῖν; αἶσθησις, δόξα) sowie von Denken und wirklichem Sein (νοεῖν, εἶναι), findet die Logik in dem größten Forscher des Altertums, in Aristoteles, ihren Begründer und Meister.
[S. 9]
Aristoteles (384-322 vor Chr.) ist der erste, der die Logik als wissenschaftliche Disziplin selbständig und ausführlich behandelt. Die Bezeichnungsart „Logik“ freilich rührt nicht von ihm her. Erst Spätere nennen die von ihm begründete und zunächst als Analytik bezeichnete Wissenschaft eine λογικὴ τέχνη (sprich: lŏgikḗe tĕ́chnēe), d. h. eine Kunst des Denkens oder Vernunftkunst; und zur Zeit Ciceros ist der Name „Logica“ bereits völlig üblich. Aristoteles selbst hat die von ihm zuerst erkannten logischen Probleme in einer Reihe von Schriften behandelt, die er je nach der Besonderheit ihres Inhalts als „Analytika protera und hystera“ (Erste und zweite Auflösungen), als „Topik“ (Beweislehre), als Schrift „über die Kategorien“ (Arten der Aussage) [Echtheit angezweifelt], als „sophistische Widerlegungen“ bezeichnet. Seine Schüler haben alle diese ihrem Gegenstande nach zusammengehörigen Schriften gesammelt und unter dem gemeinsamen Titel „Organon“ (Werkzeug; im Sinne eines Werkzeuges zur Erkenntnis der Wahrheit) vereinigt. — Im Mittelpunkt der Aristotelischen Logik steht die Frage nach den richtigen Formen des Beweises, also das Problem des gültigen Schlußverfahrens im Gegensatz zu den absichtlich-täuschenden Trug- und Fangschlüssen der Eristen und Sophisten. Diesen widmet er eine besonders gründliche Untersuchung, um die ihnen innewohnenden logischen Fehler aufzudecken und sie für immer zu entkräften. Im Gegensatz dazu stellt er drei grundlegende Arten des gültigen Beweisverfahrens auf, die sog. syllogistischen Figuren (οχήματα), die zeigen, wie man von allgemeingültigen Wahrheiten auf besondere Tatsachen schließen dürfe. Nur von hier aus und unter dem Gesichtspunkte dieses Problems behandelt Aristoteles auch die anderen uns heute geläufigen Probleme der Logik: die Fragen nach dem Wesen des Begriffs, nach Wesen und Arten der Urteile, die Fragen der Methodenlehre. Nichtsdestoweniger kommt er auch über diese zum Teil zu tiefgründigen Einsichten. Aristoteles bereits entwickelt Ansätze zu einer Kategorienlehre; er stellt den Satz des Widerspruches und den vom ausgeschlossenen Dritten auf; er berührt und erörtert das Problem der Induktion, die er „ἐπαγωγή“ (Ĕpagōgḗ) nennt; und er ist ebenso der erste, der das Wesen der Definition und Klassifikation einer tiefergreifenden Untersuchung unterzieht. Nur eines hat Aristoteles der Logik in ihrem Aufbau mitgegeben, das ihr in ihrer späteren Entwicklung verhängnisvoll werden sollte: d. i. die Vermengung der logischen mit der metaphysischen Fragestellung. Aristoteles nämlich betrachtet die Begriffe, in denen wir die Dinge denken, schlechthin als Abbilder des Wesens der Dinge, mithin die Formen und Gesetze des Denkens (Kategorien, Axiome) als die Formen und Gesetze des Seins. Damit hat Aristoteles, der Vater der formalen Logik, auch die sog. metaphysische Logik ins Leben gerufen und so zwar die Logik begründet, aber sie bereits von vornherein in ihrer eigenen Entwicklung gehemmt, wie denn ihre Befreiung von der Metaphysik erst einer späten Zeit unter schweren Kämpfen gelingen sollte.
Die Entwicklung der Logik nach Aristoteles im Altertum und Mittelalter zeitigt keine Ergebnisse von besonderer Bedeutung. Seine Schüler — Theophrast, Eudemos, Andronikos von Rhodus, Alexander von Aphrodisias u. a. — begnügen sich im allgemeinen damit, die Lehre[S. 10] des Meisters zu kommentieren und zu verbreiten; nur einige von ihnen ergänzen sie durch unwesentliche Einzelheiten. Sowohl die Epikureer wie die Stoiker und Neuplatoniker beschäftigen sich mit logischen Fragen. Insbesondere die Stoiker (Zenon, Chrysippos) erweitern die Aristotelische Schlußlehre um die Arten der hypothetischen und disjunktiven Schlüsse und stellen eine neue reifere Kategorienlehre auf. Dennoch bleibt das Fundament der Aristotelischen Logik im wesentlichen unberührt und unverändert. Nicht viel anders liegen die Dinge während des gesamten Mittelalters. Selbst die bedeutendsten Vertreter der Scholastik (Albertus Magnus; Thomas von Aquino; Duns Scotus) schöpfen wie in der Metaphysik so in der Logik aus den Schriften des Aristoteles und vermengen mehr noch als dieser selbst — (der gesamte Universalienstreit ist dafür der beste Beweis) — die logischen Fragen mit metaphysischen und grammatischen. Dennoch hat das Mittelalter das unbestreitbare Verdienst, die Aristotelische Logik im Bewußtsein der denkenden Menschheit lebendig erhalten zu haben. Besonders Petrus Ramus (aus der Übergangsepoche zwischen Mittelalter und Neuzeit) ist hier zu nennen, der der Logik als erster eine Einteilung gegeben hat, die zum Teil noch bis heute die gebräuchliche geblieben ist.
Die Geschichte der neueren Logik beginnt mit der Geschichte der neueren Philosophie. Bacons großangelegtes Programm einer neuen Wissenschaft auf Grund einer neuen wissenschaftlichen Methode (vgl. sein Hauptwerk „Novum Organon“, 1620), sein Kampf gegen die Herrschaft des Aristoteles bleiben im Stimmengewühl der Zeit nicht ungehört. Und wenn Bacon selbst auch nur umzustürzen, nicht aufzubauen versteht, so verbindet er sich doch dem Geiste nach mit denen, die den Ruf nach Reformen im wissenschaftlichen Denken nicht nur laut werden lassen, sondern auch in die Tat umsetzen. Auf dem Boden des Cartesianischen Rationalismus, in Verbindung mit der altaristotelischen Tradition, und befruchtet durch den englischen Empirismus, besonders durch Locke und Hume, wächst wie die neuere Philosophie auch die neuere Logik[1].
Descartes selbst hat der Logik kein besonderes Werk gewidmet; dennoch beschäftigt er sich in fast allen seinen Schriften — so besonders[S. 11] in der ersten, betitelt: „Regulae ad directionem ingenii“ (Regeln zur Leistung des Verstandes) — mit logischen Fragen und weist damit seine Schüler unausgesprochen direkt auf ein neu zu schaffendes System der Logik hin. Tatsächlich erwachsen aus der Cartesianischen Schule drei Logiken von Bedeutung: 1. die sog. „Logik von Port-Royal“, als deren Verfasser Antoine Arnauld und Pierre Nicole gelten (zuerst erschienen 1662); 2. die Logik des als Okkasionalisten bekannten Arnold Geulincx und 3. die Logik des als deutschen Cartesianers bekannten Johannes Clauberg. Die speziellen Anregungen, die Descartes für eine Reform der Logik gegeben hat, gehen fast durch den ganzen Bestand seines Systems hindurch. Descartes untersucht den Begriff der Wahrheit und stellt als Kriterien der wahren Erkenntnis die klare und deutliche Einsicht auf. Er untersucht die Methoden der wissenschaftlichen Forschung und unterscheidet als solche die Intuition, Deduktion und Induktion: die Intuition als Quelle absolut-gewisser, weil unmittelbar-einleuchtender Wahrheiten; die Deduktion als Ableitung spezieller Erkenntnisse aus allgemeinen und die Induktion als eine Art vollständiger, methodisch-geordneter Aufzählung (enumeratio) von Gegenständen (die Epagoge des Aristoteles). Er entwickelt ferner eine eigene Theorie des Urteils und des Irrtums (die im Kern freilich mit ähnlich-gewendeten Gedanken bei Augustin übereinstimmt), wonach nicht der Verstand das eigentlich urteilende Element in uns ist, sondern der Wille, der das vom Verstande klar und deutlich oder auch verworren bzw. dunkel Erkannte bejaht oder verneint.
Andere wesentliche Anregungen kommen der Logik etwa gleichzeitig aus England. Dort beschäftigt sich Thomas Hobbes (1588-1679) mit logischen Problemen, so mit der Frage nach dem Wesen des Denkens, das er als eine Form des Rechnens (Addierens und Subtrahierens von Begriffen und Definitionen) faßt, ferner mit dem Verhältnis von Sprechen und Denken, wobei er die Worte (terms; nomina) als Zeichen oder Symbole der Vorstellungen deutet. Von größerer Bedeutung als er ist für die Entwicklung der Logik John Locke (1632 bis 1704[2]), der diese durch seine grundlegenden Untersuchungen über Ursprung, Arten und Gewißheit der Erkenntnis in mannigfacher Weise[S. 12] bereichert, wenngleich er — infolge der von ihm auch gegenüber logischen Problemen angewandten psychologischen Methode — ungewollt der eigentliche Begründer der sog. psychologisierenden Logik geworden ist, einer heute noch nicht erstorbenen Richtung, die die Logik entweder ganz in eine psychologische Disziplin umzugestalten sucht oder doch zum wenigsten die oben gekennzeichneten Aufgaben der Psychologie des Denkens und der Logik nicht reinlich voneinander scheidet. Psychologisierend ist, was die Logik betrifft, auch das Verfahren David Humes (1711-1776); dennoch hat Hume in der Entwicklung der Logik das große Verdienst, in seinen grundlegenden Untersuchungen über das Problem der Kausalität die moderne Theorie der Induktion vorbereitet zu haben, als deren unmittelbarer Vorläufer, wenn nicht gar Begründer, er darum bezeichnet werden muß (vgl. B. Erdmann, Logik I2, S. 781).
Auch die deutsche Philosophie des 17. und 18. Jahrhunderts weist eine reiche logische Entwicklung auf. Dem im Geiste Descartes’ gehaltenen Werke Claubergs folgt wenig später die auch Spinozistische Einflüsse verratende „Medicina mentis“ (Gesundheitslehre des Geistes) des Grafen Ehrenfried Walter von Tschirnhausen; und zur gleichen Zeit etwa beginnt auch Leibniz durch den gewaltigen Bau seines philosophischen Systems auf die Entwicklung der Logik befruchtend einzuwirken. Leibniz (1646-1716) selbst hat zwar ebensowenig wie Descartes die Grundlagen der Logik systematisch abgehandelt; aber er hat doch fast alle logischen Probleme der Zeit, wenn nicht direkt erörtert, so doch zum mindesten gestreift. Er fügt dem von Aristoteles aufgestellten Satz des Widerspruchs den sog. logischen Satz vom zureichenden Grunde hinzu und scheidet entsprechend diesen beiden Grundsätzen die wissenschaftlichen Erkenntnisse in zwei Gruppen: in die „vérités de fait“ (Tatsachenwahrheiten) und die „vérités de raisonnement“ (Vernunftwahrheiten). Er nimmt Stellung zu dem Descartes-Lockeschen Problem der angeborenen Ideen und Wahrheiten; er klassifiziert — gründlicher als vor ihm Descartes und Locke — die Erkenntnisse in klare und dunkle bzw. deutliche und verworrene und betont nachdrücklich die für die Logik zu begründende Lehre von der Wahrscheinlichkeit.
Was die Verfasser der Logik von Port-Royal gegenüber Descartes, dasselbe leistet Christian Wolff (1679-1754) gegenüber Leibniz. Wolff bringt die Gedanken, die er bei Leibniz gefunden hat (wobei[S. 13] übrigens auch gewisse andersher gerichtete Einflüsse nicht übersehen werden dürfen), in ein System. Durch die breite, ausführliche, das Wesentliche wie das Unwesentliche gleichermaßen erschöpfend behandelnde Darstellung, die er der Logik sowohl in seinem lateinischen Werke „Logica“ (zuerst 1728) wie in dem deutschen, betitelt: „Vernünftige Gedanken von den Kräften des menschlichen Verstandes“ (zuerst 1712), angedeihen läßt, popularisiert er die Grundlagen des logischen Lehrbestandes seiner Zeit und wird damit zum Urheber einer ausgebreiteten logischen Literatur, die zwar ihre Wissenschaft nur wenig zu bereichern oder zu verbessern vermag, aber sie doch zum Gemeingut aller in jener Zeit wissenschaftlich interessierten Kreise der Bevölkerung macht. Aus der Reihe der Logiker dieser Epoche, die übrigens die Logik fast ausnahmslos als eine normative Disziplin abhandeln, deren Aufgabe darin bestehe, richtiges Denken zu lehren, ragen als die bekanntesten hervor: Georg Friedrich Meier; Hermann Samuel Reimarus; Gottfried Ploucquet; Johann Heinrich Lambert sowie Christian August Crusius.
Es muß beinahe als eine besondere Eigentümlichkeit in der Geschichte der Logik angesprochen werden, daß gerade die Männer, die diese Disziplin am meisten angeregt und gefördert haben, ihr selbst kein besonderes oder doch zum mindesten kein größeres Werk gewidmet haben. Wie das für Descartes, Locke und Leibniz gilt, so auch für Kant[3]. Wie durch Kant für die Philosophie überhaupt, so beginnt auch für die Logik eine neue Epoche. Kant selbst hat zwar vermeint, daß die Logik bereits durch Aristoteles einen so vollendeten Ausbau gefunden habe, daß sie seitdem weder einen Schritt vorwärts habe tun können noch auch einen Schritt zurück habe tun müssen. Nichtsdestoweniger ist gerade er es, der die Logik weit über Aristoteles hinaushebt. Kant betont in erster Linie den formalen Charakter der eigentlich und so zu nennenden Logik, die er als allgemeine von der sog. transzendentalen Logik scheidet. Die transzendentale Logik, die er in der „Kritik der reinen Vernunft“ abhandelt, untersucht das Erkenntnisvermögen des Menschen auf seine apriorischen Elemente, soweit diese dem Verstande angehören, d. h. auf diejenigen Elemente der Erkenntnis, die als reine Verstandesbegriffe unabhängig von der[S. 14] Erfahrung sind und als solche dieser Gesetz und Regel vorschreiben; eine Disziplin, die zu einem Teil etwa der heute sog. Erkenntnistheorie entspricht. Die allgemeine Logik, die Kant des öfteren in Vorlesungen an der Königsberger Universität behandelt hat (unzulänglich herausgegeben von Jäsche, 1800), ist demgegenüber die Wissenschaft von den formalen Regeln alles Denkens — es mag dieses apriorisch oder empirisch sein — und untersucht das Denken, indem sie von allen Objekten der Erkenntnis und ihrem Unterschiede abstrahiert, so daß der Verstand es in ihr mit nichts anderem wie mit sich selbst und seiner Form zu tun hat. Sie erörtert und prüft also die Formen des Denkens (Begriff, Urteil, Schluß), ferner die formalen Kriterien der Wahrheit (den Satz der Identität und des zureichenden Grundes, des Widerspruches und des ausgeschlossenen Dritten). Ungeachtet dieser strengen begrifflichen Scheidung gehen die Anregungen, die Kant der Logik gegeben hat, mehr von der in der Kritik d. r. Vern. entwickelten Transzendentalphilosophie als von den Vorlesungen über die formale Logik aus. Kant stellt in der Elementarlehre der Kritik d. r. Vern. wie eine Tafel der Urteile, so auch eine Kategorientafel auf, indem er die letztere aus der ersteren ableitet. Das Schema der Urteile hat noch bis in die Gegenwart hinein für die meisten Logiker als grundlegende Einteilung der Lehre vom Urteil gegolten.
Die Geschichte der nachkantischen Logik ist von dem gleichen wechselvollen Charakter wie die Geschichte der nachkantischen Philosophie überhaupt. Fichte betrachtet die formale Logik durch die Transzendentalphilosophie, die er seinerseits durch die Wissenschaftslehre ersetzt, als überwunden (vgl. die Vorlesungen Fichtes über das Verhältnis der Logik zur Philosophie, 1812, Nachgel. Werke I). Hegel stürzt das bis dahin mühsam aufgerichtete Gebäude der Logik um, indem er diese von neuem mit metaphysischen Erörterungen durchsetzt (metaphysische Logik auf der Grundlage der Identität von Denken und Sein). Und Fries macht den Versuch, die logischen Probleme ganz und gar zu psychologisch-genetischen (nach Friesscher Terminologie: zu anthropologischen) zu gestalten. Erst Herbart und seine Schüler (besonders Drobisch) bemühen sich wieder, die Logik von ihrer Vermengung mit der Psychologie und Metaphysik zu befreien, und betonen nachdrücklich ihren formalen Charakter.
In der neueren Logik — etwa seit der Mitte des 19. Jahrhunderts — sind wieder alle Richtungen vertreten, die auch in der älteren Geschichte[S. 15] miteinander um die Palme ringen. Neu zu nennen sind nur gewisse Versuche in der englischen Logik seit William Hamilton und George Boole, die allerdings in älteren Denkern wie Raymundus Lullus, Leibniz und Ploucquet Vorläufer haben, die Logik im Sinne einer der Mathematik verwandten Wissenschaft abzuhandeln, worin an Stelle der Zahlen und Größen die Begriffe treten, eine Auffassungsart, die man als algebraische, arithmetische oder auch allgemeiner als mathematische Logik (Lehre vom logischen Kalkül, vom logischen Algorithmus) zu bezeichnen pflegt. In Deutschland haben diese (durch Jevons und andere in England und Amerika weitergeführten) Versuche, die das Wesen der Denkoperationen eher verdunkeln als erhellen, nur wenig anregend und fördernd gewirkt (vereinzelte Anhänger sind Rob. Graßmann, Joseph Hontheim, besonders Ernst Schröder); um so mehr jedoch andere aus England kommende philosophische Strömungen, wie z. B. die grundlegenden Untersuchungen von John Stuart Mill, dem Hauptvertreter der sog. induktiven Logik, sowie von Herbert Spencer und William Stanley Jevons zur wissenschaftlichen Methodenlehre.
Wie das Problem der Methode so steht auch das Problem des Urteils im Mittelpunkte der neueren logischen Untersuchungen. Die Frage nach dem Wesen des Urteils, d. h. nach dem Sinne der prädikativen Beziehung zwischen Subjekt und Prädikat, wird zum Hauptproblem der Elementarlehre. Aber ihre Erörterung begegnet durch die immer wieder nachhaltende, vornehmlich von Husserl mit Erfolg bekämpfte Vermengung der psychologischen mit der logischen Fragestellung zunächst großen Schwierigkeiten. Die psychologisierende Logik zeigt ihren Einfluß auch gegenwärtig allerorten; sie findet sich nicht nur herrschend bei solchen Denkern, die wie ursprünglich Theodor Lipps sich offen zu ihr bekennen, sondern auch zum Teil bei solchen, die mit gutem Glauben vorgeben, eine psychologiefreie formale Logik zu vertreten. Anderseits aber tritt an Stelle der metaphysischen Logik im Sinne Hegels neuerdings die sog. erkenntnistheoretische Logik, die zwischen der erkenntnistheoretischen und logischen Problemstellung keinen prinzipiellen Unterschied anerkennt (Trendelenburg; Überweg; Schuppe; ebenso Wundt; in anderer Hinsicht auch: Cohen und Natorp). Gegenüber diesen Richtungen haben die Vertreter der formalen Logik im Sinne der Kant-Herbartschen Tradition nicht immer leichten Stand. Die fundamentalen[S. 16] Hauptarbeiten dieser Richtung sind die Werke von Chr. Sigwart und B. Erdmann. So sehr auch diese wiederum in wesentlichen Punkten voneinander abweichen, so ist doch das ihnen richtunggebende Ziel das gleiche: die Ausschließung alles Metaphysischen aus der Logik und die möglichst reinliche Trennung der logischen von der erkenntnistheoretischen und psychologischen Problemstellung. Diesem Ziel ist von den zuletzt genannten Denkern B. Erdmann am nächsten gekommen. Darin vor allem sowie in der von ihm aufgestellten Theorie des Urteils, des Syllogismus und der Induktion, liegt das besondere Verdienst Erdmanns; in der mannigfachen Förderung der wissenschaftlichen Methodenlehre das besondere Verdienst Sigwarts um die Fortbildung der Logik.
[1] Über die Entwicklung der neueren Philosophie im allgemeinen vgl. Ludwig Busse. Die Weltanschauungen der großen Philosophen der Neuzeit (ANuG Bd. 56).
[2] Zum folgenden vergleiche man P. Thormeyer, Locke, Berkeley, Hume (ANuG Bd. 481).
[3] Man vergleiche zum folgenden Oswald Külpe, Immanuel Kant (ANuG Bd. 146).
Die Beziehungen zwischen Sprechen und Denken bilden ein altes philosophisches Problem. Schon Platon hat gelegentlich bemerkt, daß das Sprechen ein lautgewordenes Denken, das Denken ein stilles Sprechen sei (Sophistes). Dieser Identifizierung von Sprechen und Denken, die beides solchermaßen in eins setzt, daß eines ohne das andere unmöglich erscheint, steht jene Auffassung gegenüber, die zwischen dem Denken und Sprechen streng scheidet und die Sprache nur als eine Art Gewand oder äußere Hülle des Gedankens ansieht, welche dem Denken lediglich zum Zwecke der Mitteilung gegeben und ihm unabhängig davon eher schädlich sei als nütze (Lehre der Mystiker).
Wie man zwischen diesen extremen Theorien entscheiden soll, hängt von den Ergebnissen einer anzustellenden psychologischen Analyse ab. Wenn wir auf uns achten, sobald wir mit einer Sache gedanklich beschäftigt sind, so finden wir, daß die Funktionen des Denkens meist an die Elemente der Sprache gebunden sind. Wir denken vermittels der Worte, die wir zu Sätzen aneinanderreihen und deren Sinn wir verstehen. Auch dann, wenn wir den Verlauf unserer Gedanken nicht anderen mitteilen, sondern still für uns denken (stilles Denken),[S. 17] ist dieser Prozeß meist an Worte und daraus gebildete Sätze geknüpft. Danach würde Platon recht zu haben scheinen, daß alles Denken ein sprachliches, ein Denken ohne Sprache mithin nicht möglich sei. Nun aber gibt es in unserem Bewußtsein zweifellos gewisse dem sprachlichen Denken verwandte Vorgänge, die sich ohne jede Hilfe von Worten lediglich durch Verknüpfungen von Vorstellungen auf Grund der Inhalte der Wahrnehmung und des Gedächtnisses vollziehen. Beispiele dafür sind die Fülle von Vorstellungen der Erinnerung und Einbildung, die in jemandem erwachen, der etwa in reifem Alter die Stätten seiner Jugend betritt, oder der Pläne zu einer Reise zurechtlegt in Gegenden, die ihm durch früheren Aufenthalt ganz oder zum Teil bekannt sind. In diesen und ähnlichen Fällen können alle Wortvorstellungen im Bewußtsein fehlen, und doch in dem Vorstellenden Erkenntnisse und Entschlüsse von Bedeutung reifen. Will er diese freilich sich völlig klar zu Bewußtsein bringen oder gar anderen mitteilen, so muß er sie in Worte fassen (sprachlich formulieren); konzipiert aber hat er sie doch ohne jede Beihilfe der Sprache.
Damit hätte die psychologische Analyse des Verhältnisses von Denken und Sprechen zwei verschiedene Arten des Denkens ergeben: ein sprachliches und ein unsprachliches, in der neueren Psychologie (so von B. Erdmann) als formuliertes und intuitives Denken bezeichnet. Diese beiden Arten des Denkens sind jedoch nicht gleichwertig. Ohne Zweifel steht das formulierte Denken seinen Leistungen nach unvergleichlich über dem intuitiven, und dem letzteren kommt ein gewisser Wert überhaupt nur dadurch zu, daß uns die Möglichkeit gegeben ist, das bloß intuitiv Gedachte in Worten zu formulieren. Wäre diese Möglichkeit uns versagt, so ständen wir darin auf der Stufe der Tiere, die — ebenso wie die Kinder vor Beginn der Spracherlernung — nur die Fähigkeit des intuitiven, nicht aber des formulierten Denkens besitzen. Aus diesem Grunde haben manche Psychologen es vermieden, das intuitive Denken überhaupt als ein Denken im eigentlichen Sinne zu bezeichnen, und den Begriff Denken auf das formulierte beschränkt. Wie man sich in der Psychologie zu dieser rein terminologischen Frage stellen mag, soll hier nicht weiter erörtert werden. Den Zwecken der Logik jedenfalls, bei deren Untersuchung der Formen des Denkens allein das formulierte in Betracht kommt, ist es angepaßter, den Begriff des Denkens, wo er verwandt wird, stets im Sinne des formulierten zu verstehen.
[S. 18]
Diese propädeutisch für die Logik entwickelte Bestimmung, die das Denken ganz allgemein als einen Inbegriff von an die Funktionen der Sprache gebundenen Vorgängen kennzeichnet, betont zwar die Bedeutung der Sprache für das Denken, identifiziert diese mit jenem aber keineswegs. Hören wir beispielsweise einen Vortrag in einer uns unbekannten Sprache, so werden unseren Ohren zwar Schallwirkungen, dem Gehörsinn zwar Geräusche, die wir als Worte deuten, dem Verstande aber keine Gedanken vermittelt. Das Denken (sowohl das stille, das wir für uns vollziehen, wie das laute formulierte Denken) ist also wohl an die Mittel der Sprache gebunden, seinem Wesen nach aber ganz etwas anderes als diese. Das bloße Wort ist an und für sich Schall und Rauch; erst das Verständnis des Wortes ermöglicht den Gedanken. Worte sind mithin Träger, wenn wir zu anderen sprechen, Vermittler von Gedanken; nicht sie, sondern ihre Bedeutungsinhalte bilden die Grundlagen des Denkens. Darum rufen zwei- oder mehrdeutige Worte (Äquivokationen) leicht Mißverständnisse hervor; darum bedarf jede auf genaues Verständnis der Teilnehmer abzielende Erörterung oder Auseinandersetzung einer Terminologie, innerhalb deren jedes nicht eindeutige Wort in fest umgrenztem, nicht mißzuverstehendem Sinne bestimmt ist.
Nichtsdestoweniger sind die Elemente der Sprache für das Denken in seinen beiden Formen des Eigendenkens und des Nachdenkens (das letztere im Sinne des Verständnisses von Gehörtem und Gelesenem) so bedeutungsvoll, daß andere wie Wortvorstellungen dabei im Bewußtseinsbestande völlig fehlen können. Diese Auffassung widerspricht einer bereits alten, weit verbreiteten Theorie, die das Denken — wenn nicht etwa ganz in ein Verknüpfen bzw. Trennen oder Zerlegen von Vorstellungen auflöst — so doch ohne das Vorhandensein von Vorstellungen der gedachten Gegenstände als unmöglich erklärt[4]. Demnach komme das Verständnis der Worte in uns dadurch zustande, daß wir uns die durch sie bezeichneten Objekte anschaulich vorstellen, und zwar gemeinhin durch abstrakte Allgemeinvorstellungen jener Objekte. So hat z. B. Locke gelegentlich gemeint, der Gattungsbegriff „Dreieck“ werde gedacht durch die abstrakte Allgemeinvorstellung eines Dreiecks, welches weder schiefwinklig noch[S. 19] rechtwinklig, weder gleichseitig noch gleichschenklig noch ungleichseitig, sondern dieses alles und zugleich nichts davon sei.
Schon George Berkeley (1684-1753) hat gegenüber dieser Theorie darauf hingewiesen, daß es nach einer sorgfältigen Prüfung, die er angestellt habe, abstrakte Allgemeinvorstellungen dieser Art nicht gebe. Was man mit der Vorstellung eines Dreiecks, das weder schiefwinklig noch rechtwinklig, weder gleichseitig noch gleichschenklig noch ungleichseitig sei, meine, wisse er nicht. Er seinerseits könne in seinem Bewußtsein beim Denken nur Einzelvorstellungen entdecken, die als solche Repräsentanten der gesamten Gattung bilden. Der Sinn des Wortes „Dreieck“ z. B. könne verstanden werden durch die Vorstellung eines beliebigen Dreiecks, das in sich die gesamte Gattung „Dreieck“ repräsentiere. Aber es sei auch sehr wohl möglich, ihn lediglich auf Grund des Wortes zu erfassen und ohne jegliche Vermittlung einer Vorstellung. (Ähnliches später bei Schopenhauer.)
Die neuere experimentelle Psychologie des Denkens hat diese Auffassung glänzend bestätigt. Arbeiten von Bühler, Messer, Ach u. a. haben einwandfrei erwiesen, daß wir ganze Zusammenhänge denken können, ohne daß auch nur die geringste Vorstellung der gedachten Objekte in unserem Bewußtsein wach wird, dergestalt, daß Sinn und Verständnis lediglich in und mit den Worten gegeben ist[5]. Daraus folgt, daß das Wort für das Denken — zum mindesten für das entwickelte Denken — einen ungleich wichtigeren Faktor bedeutet als die Vorstellung. Wort und Begriff verhalten sich — nach einem treffenden Ausspruch Riehls — zueinander wie Organ und Funktion. Wohl ist es beinahe die Regel, daß — infolge der Tatsachen der Assoziation und Reproduktion — Vorstellungen unser Denken begleiten, die uns die gedachten Gegenstände optisch, akustisch oder wie sonst immer repräsentieren. Aber diese Vorstellungen sind nicht Bedingungen des Denkens: d. h. sie gehören nicht notwendig dazu; sondern sie bilden lediglich eine Art Denk-Hilfen zum schnelleren und besseren Verständnis, die je nach dem Gegenstande des Denkens und den individuellen Eigentümlichkeiten des Denkenden fehlen können, ja sogar beim entwickelten Denken des reifen Menschen, besonders[S. 20] wo es sich um abstrakte oder häufig wiederholte Gedankengänge handelt, überaus oft fehlen. Demgegenüber wird natürlich das Kind erheblich mehr Sachvorstellungen im Bewußtsein haben als der Erwachsene; denn hier sind die Assoziationen zwischen Wort und Vorstellung noch frisch und nicht durch jahrelange Übung und Gewohnheit so mechanisiert, daß dem Worte das Verständnis unmittelbar, nicht durch die Hilfe einer Vorstellung folgt.
Gegenstand des Denkens kann alles werden, was in irgendeiner Gestalt in unser Bewußtsein eingeht: die räumlich-ausgedehnten Objekte der sog. „Außenwelt“ mit ihren Farben, Tönen, Gerüchen und deren Beziehungen untereinander ebenso wie die psychischen Phänomene des Denkens und Vorstellens, Fühlen und Wollens. Sieht man von der oben gekennzeichneten Art des intuitiven Denkens ab, so kann ein Gegenstand erst dann von uns gedacht werden, wenn er benannt ist. Für das Denken ist es an und für sich gleichgültig, wie man einen Gegenstand bezeichnet. Wenn es jemandem einfiele, der erfinderisch genug dazu wäre, sich eine eigene Sprache zu schaffen, so könnte er darin auf seine Weise alles ausdrücken, wie es ihm beliebte (Geheimsprachen, Diplomatensprachen); nur die Möglichkeit einer Verständigung mit anderen wie Eingeweihten wäre für ihn dann aufgehoben. Da aber die Sprache gemeinhin den Bedürfnissen der Mitteilung dient, ist es erforderlich, daß die Verbindung zwischen Wort und Bedeutung für alle die, welche Gedachtes mitteilen und Mitgeteiltes verstehen wollen, eine den Sprachgewohnheiten nach in gewissen Grenzen beharrende sei.
Gegenüber der gewaltigen Fülle von Objekten, die als mögliche Gegenstände des Denkens in unser Bewußtsein eingehen, hat das menschliche Denken eine Leistung von hervorragender Ökonomie geschaffen. Die psychologischen Tatsachen der Erinnerung und des Wiedererkennens, des Vergleichens und Unterscheidens, der Abstraktion und Determination haben es mit sich gebracht, daß das Denken nicht je ein besonderes Wort für jeden einzelnen Inhalt des Bewußtseins geprägt, sondern immer ganze Gruppen ähnlicher Objekte unter einem gemeinsamen Namen zusammengefaßt hat. Diesem allmählich[S. 21] sich entwickelnden Prozeß der Benennung der Gegenstände analytisch nachzugehen, ist Sache der Psychologie, speziell dort, wo sie über den Ursprung und die Entwicklung der Sprache zu handeln hat, und führt über den Rahmen einer rein logischen Untersuchung hinaus. Was man gemeinhin in der Logik als Frage nach dem Ursprung der Begriffe bezeichnet, ist nichts anderes wie dieses Problem der Zusammenfassung ganzer Gruppen von Objekten unter einem Namen. Denn als Begriff bezeichnet die neuere Logik gemeinhin die Bedeutung eines Wortes, mithin das, was wir verstehen, wenn wir die Worte einer uns bekannten Sprache vernehmen (... „doch ein Begriff muß bei dem Worte sein“; Goethe, Faust). Der Prozeß der Begriffsbildung ist danach mit dem der Spracherzeugung und Sprachentwicklung aufs engste verwachsen und die Frage nach der Entstehung der Begriffe kein eigentlich logisches, sondern psychologisches Problem.
Um so mehr ist für die Logik die Frage nach der Leistung und dem Wert der Begriffe wesentlich. Verstehen wir zunächst ganz allgemein unter einem Begriff den Bedeutungsinhalt eines bekannten Wortes, so besteht die Leistung eines Begriffes darin, einen größeren oder kleineren Ausschnitt aus der Welt der Objekte durch ein einziges Wort bequem für das Denken zugänglich zu machen. In dieser Beziehung des Begriffes auf einen engeren oder weiteren Kreis von Gegenständen vermittels eines einzigen Wortes liegt seine Bedeutung; zugleich wurzelt darin seine wesentlichste Eigenschaft, der Charakter der Abstraktheit. Alle Begriffe an und für sich sind ihrem Wesen nach abstrakt. Die übliche Unterscheidung zwischen Konkret und Abstrakt bezieht sich nicht auf Begriffe, sondern auf Gegenstände (Riehl). Begriffe haben stets abstrakten Charakter, selbst diejenigen, in denen wir die konkretesten Dinge denken. Begriffe von Individuen sind dabei weniger abstrakt als Begriffe, die sich auf Arten oder Gattungen beziehen (z. B. Napoleon, Verona im Vergleich zu: Türke, Koralle); Begriffe von der Allgemeinheit wie Menschheit, Schönheit, Wachstum (sog. Kollektivbegriffe) sind wiederum von abstrakterer Natur als Gattungsbegriffe wie: Mensch, schön und wachsen. Der Grad der Abstraktheit eines Begriffes richtet sich dabei nach dem Maße, in dem sein Gegenstand der Anschauung näher oder ferner steht. Die höchsten und allgemeinsten Begriffe sind mithin die am meisten, die niedersten und speziellsten die am wenigsten abstrakten.
[S. 22]
Heben wir aus dem Bisherigen das Wesentliche hervor und ziehen wir daraus die notwendigen Konsequenzen. Wir denken die Objekte der äußeren und inneren Welt mit ihren Qualitäten und Beziehungen nicht in den Wahrnehmungen der Sinne, nicht in den Vorstellungen der Erinnerung, Einbildung oder Abstraktion, die unser Bewußtsein erfüllen, auch nicht in den Worten, mit denen wir diese Objekte bezeichnen, sondern in und mit den Begriffen, die uns durch Worte vermittelt und gegeben, einen mehr oder weniger großen Umkreis von Objekten zu einem einzigen Gegenstand des Denkens erheben. Was Begriffe sind, kann jeder an sich selbst beobachten, der den Sinn der Bezeichnungen einer ihm bekannten Sprache versteht. Den Begriff „Lieblichkeit“ versteht jeder, der ihn hört und mit der deutschen Sprache vertraut ist, auch ohne daß er sich etwa irgendwelche Objekte von lieblichem Aussehen oder Klange vorstellte, oder eine daraus gebildete abstrakte Allgemeinvorstellung in ihm wach würde. Was in mir vorgeht, wenn ich das Wort „Lieblichkeit“ in dem Urteil: „Lieblichkeit ist ein Geschenk Gottes“ denke, ist in der Tat keine besondere Vorstellung (obschon das wohl der Fall sein könnte!), insbesondere keine abstrakte Allgemeinvorstellung, die durch Abstraktion und Determination aus tausend oder noch mehr lieblichen Gegenständen meiner Wahrnehmungen und Erinnerungen gewonnen wäre, sondern ist ein unmittelbares Wissen und Verstehen dessen, was mit dem Worte gemeint ist (in der neueren Psychologie bei Bühler benannt als: „Gedanke“; bei Ach als: „Bewußtheit“). Ich könnte die Bedeutung des Wortes, wenn man es von mir verlangte, definieren; ich könnte, falls diese Definition nicht exakt genug ausfiele, zum mindesten den Sinn des Wortes beschreiben, durch Beispiele erläutern oder durch Gleichnisse versinnbildlichen. Kurzum: dieses Wissen um die Bedeutung des Wortes macht seinen Begriff aus. Der Begriff ist danach logisch seiner Definition gleich zu erachten, nur daß der Begriff implicite (unentfaltet) enthält, was die Definition (oder Begriffsbestimmung) explicite (entfaltet) darlegt (vgl. A. Riehl, Beiträge zur Logik, 2. A. S. 12 f.). An dieser Theorie wird auch dadurch nichts erschüttert, daß die Begriffe des gemeinen Volkes andere sind wie die der Wissenschaft. Den vollkommenen Begriff eines Gegenstandes hat nur der, der ihn in wissenschaftlicher Weise zu bestimmen vermag. Dem nichtwissenschaftlichen Zwecken angepaßten Denken der großen Menge genügt es, wenn es den Sinn der sprachlichen Bezeichnungen, die seinen Wortschatz bilden,[S. 23] in nichtwissenschaftlicher Weise zu bestimmen weiß. Es ist ein ideales Ziel aller Volksbildungsversuche, die unklaren Begriffe der Menge zu immer klareren zu erheben. Ein Begriff des praktischen Denkens ist um so klarer, je mehr seine Definition den wissenschaftlich gesicherten Ergebnissen über seinen Gegenstand entspricht. Alle Popularisierung von wissenschaftlichen Resultaten führt darum, wo es maßvoll und zweckentsprechend geschieht, zu einer Klärung der Begriffe des Volkes und damit zu einem höheren Stande der Volksbildung überhaupt. „Vollkommen“ sind die Begriffe der Wissenschaft (mit Ausnahme gewisser grundlegender mathematischer Begriffe) auch nur in relativem Sinne oder ihrer idealen Forderung nach. Gilberts Begriff der elektrischen Anziehung (vor 1600) — für seine Zeit höchst bedeutsam — ist nach Lage der Dinge unendlich viel ärmer als der moderne Begriff der Elektrizität. Aber auch dieser Begriff wiederum ist nur in höchst relativem Sinne als „vollkommen“ zu bezeichnen, wie wir denn hoffen dürfen, daß eine fortschreitende Erkenntnis auch unseren Begriff der Elektrizität einmal als ärmlich und unzureichend erkennen wird.
In und mit jedem Begriff, der in unser Denken eingeht, erfassen wir einen eigentümlichen Inhalt, der diesen Begriff bestimmt, ihn zugleich als besonderen Begriff kennzeichnet und von allen anderen Begriffen unterscheidet. Nehmen wir beispielsweise den Begriff „Schwan“, so versteht man darunter, wofern man mit den zoologischen Eigentümlichkeiten dieses Tieres vertraut ist, einen großen, sehr langhalsigen, aber kurzbeinigen Schwimmvogel von der Art der Entenvögel, mit an der Spitze abgeplattetem Schnabel, der in der gemäßigten und kalten Zone lebt, in der nördlichen Halbkugel weiß, in der südlichen ganz oder teilweise schwarz gefärbt ist. Der Begriff „Schwan“ hat mithin zum Gegenstand eine Art der Schwimm-, genauer der Entenvögel; als Inhalt die besonderen Eigenschaften des sehr langen Halses, der kurzen Beine, des abgeplatteten Schnabels usw., die den Schwan von anderen Schwimmvögeln unterscheiden und ihn als Schwan kenntlich machen.
Der Inhalt eines Begriffes ist es danach, der das Wesen des Begriffes ausmacht. Bestehend aus dem Inbegriff der Merkmale, die den betreffenden Gegenstand charakterisieren, bildet er dasjenige Element, durch das wir den Begriff als das, was er ist, denken und[S. 24] ihn von allen anderen Begriffen absondern. Der sog. logische Grundsatz der Identität (in der traditionellen Logik zumeist an unpassendem Platze in der Urteilslehre erwähnt), dargestellt durch die Formel: „A ist A“, besagt nichts anderes wie, daß jeder Begriff, bestimmt und gekennzeichnet durch einen ihm zugehörigen Inhalt, von uns als mit sich selbst identisch und verschieden von allen anderen Begriffen gedacht wird. („Jeder Begriff ist mit sich selbst identisch.“)
Ein Begriff ist das, was er ist, durch seinen Inhalt. Begriffe sind einander gleich (identisch), auch wenn sie mittels verschiedener Worte sprachlich fixiert sind, sofern in ihnen der gleiche Inhalt gedacht wird (Grundsatz der Synonyme). Begriffe sind verschieden, auch wenn sie durch ein und dasselbe Wort ausgedrückt werden, wofern in ihnen ein verschiedener Inhalt gedacht wird (Grundsatz der Äquivokationen). Der Begriff darf also nicht etwa als eine Art „stetiger Funktion“ des Wortes gedeutet werden, an das er geknüpft ist. Worte können abweichende Bedeutung haben je nach dem Zusammenhang, in den sie eingeordnet sind, und damit also auch verschiedenen, wenn auch zumeist verwandten Begriffen dienen. Schon daraus allein ergibt sich, was sich in einem späteren Zusammenhange noch deutlicher erweisen wird, daß Begriffe an und für sich unselbständige Elemente des Denkens sind. Alles Denken geschieht durch Urteilen oder Fragen, und das Fragen hat, wie sich noch zeigen wird, seiner logischen Funktion nach selbst wieder Urteilscharakter. Das Urteil ist, logisch wie psychologisch genommen, dem Begriff (und auch dem Schluß) gegenüber das Ursprünglichere; es ist mithin das Formelement des Denkens, zu dem sich die Begriffe etwa verhalten wie Protoplasma, Kern und Membran zur Zelle als dem Formelement des organischen Lebens.
Der Inhalt eines Begriffes zerfällt nach den Merkmalen, die in ihm enthalten sind, in einen Inhalt im engeren und im weiteren Sinne. Der Inhalt im engeren Sinne oder konstituierende Inhalt ist der Inbegriff der Merkmale eines Gegenstandes, ohne die dieser schlechthin nicht gedacht werden kann, weil sie ihm seinem Wesen nach als bestimmend und darum notwendig zugehören (wesentliche oder notwendige Merkmale); der Inhalt im weiteren Sinne oder auch mögliche Inhalt ist der Inbegriff derjenigen Merkmale, die dem Gegenstande seinem Wesen nach zukommen können, aber nicht notwendig zukommen müssen (mögliche oder unwesentliche[S. 25] Merkmale). Insofern nun alles, was von einem Gegenstand urteilsmäßig ausgesagt werden kann, entweder dem Inhalt im engeren oder dem Inhalt im weiteren Sinne angehören muß, nennt man den Inbegriff dieser beiden auch den prädikativen (aussagbaren) Inhalt eines Begriffes.
Diese Scheidung sei durch ein Beispiel verdeutlicht. Unter dem Begriff „Uhr“ versteht man ganz allgemein eine von Menschen geschaffene Einrichtung, deren Zweck es ist, entsprechend der Einteilung des Tages in 24 Stunden, der Stunde in 60 Minuten usw. die Zeit anzugeben. Diese beiden Eigenheiten (1. Einrichtung durch den Menschen und 2. zeitmessender Zweck) bilden die wesentlichen Merkmale des Begriffes „Uhr“, die dessen konstituierenden Inhalt ausmachen, ganz gleich, ob es sich um eine Sonnenuhr, Sanduhr, Pendeluhr oder Federwerkuhr handelt. Der mögliche Inhalt des Begriffes ist dahingegen unendlich viel reicher. Man kann je nach den besonderen Umständen von der Uhr aussagen, daß sie ein nützliches oder wertloses Geschenk für die Menschheit sei; daß sie als zeitmessendes Instrument ein zweckmäßiges oder unzweckmäßiges Zahlensystem als Einteilungsmaßstab zu ihrer Voraussetzung habe, daß sie aus Gold, Silber, Kupfer, Stahl gefertigt sei u. a. m. Kurzum: der mögliche Inhalt des Begriffes umfaßt alle Merkmale, die ihm unter Umständen zukommen können, d. h. mit seinen wesentlichen Merkmalen verträglich sind.
Zu dieser Unterscheidung kommen noch fernere. Die Merkmale, die den Inhalt eines Begriffes bilden, sind entweder innere, d. h. solche, die man gewinnt, wenn man den Gegenstand des Begriffes in sich selbst analysiert („innere Analyse“); oder auch äußere (besser: Beziehungsmerkmale, Relationsmerkmale), d. h. solche, die sich aus der Vergleichung des betreffenden Gegenstandes mit anderen ergeben. Mit Rücksicht auf die letzteren hat man auch von einem „relativen Inhalt“ gesprochen, der gleich dem Inbegriff der Beziehungsmerkmale eines Begriffes ist. Endlich sind die Merkmale eines Begriffes entweder qualitative oder quantitative; ursprüngliche oder abgeleitete; eigene oder gemeinsame (vgl. B. Erdmann, Logik I2, Kap. 23).
Es ist ersichtlich, daß für die Bestimmung eines Begriffes nicht der mögliche, sondern der konstituierende Inhalt in Frage kommt. Der konstituierende Inhalt als Inbegriff der notwendigen Merkmale begründet den Begriff; der mögliche Inhalt ist demgegenüber logisch als vom konstituierenden abhängig und ableitbar zu bezeichnen. Will ich einen Begriff denken, so ist es nötig, daß ich mit seinen konstituierenden Merkmalen vertraut bin (d. h. ich muß sie wissen, obschon es nicht notwendig ist, daß sie mir alle zugleich bewußt sind); will ich einen Begriff definieren, so ist es nötig, daß ich seine konstituierenden[S. 26] Merkmale angebe. Es ist demgegenüber aber weder für das Denken noch die Definition eines Begriffes erforderlich, daß ich auch alle seine möglichen Merkmale kenne oder anzugeben weiß; denn diese sind jederzeit aus dem Inbegriff der wesentlichen Merkmale ableitbar, insofern als zum möglichen Inhalt alles gehört, was dem notwendigen nicht widerspricht. Darum haben manche Logiker unter dem „Inhalt“ eines Begriffes überhaupt nur den konstituierenden verstanden. Darum soll auch hier, wo nicht ausdrücklich zwischen beiden Arten des Inhalts unterschieden wird, überall, wo vom Inhalt schlechthin die Rede ist, der konstituierende gemeint sein.
Konstituierender und möglicher Inhalt eines Begriffes stehen zueinander in relativem Verhältnis. Der Wandel der Begriffe im Laufe der Zeiten bringt es mit sich, daß heute als einem Begriff notwendiges Merkmal gedacht wird, was gestern noch als möglich und darum unwesentlich galt und umgekehrt. Ebenso können Merkmale — entsprechend der Verschiedenheit der menschlichen Kenntnisse und Erfahrungen — dem einen als konstituierende gelten, die dem anderen als nur mögliche und darum unwesentliche erscheinen.
Die Zahl der notwendigen Merkmale, die den konstituierenden Inhalt eines Begriffes bilden, ist entsprechend der Verschiedenheit der Begriffe verschieden groß. Je nach der Größe dieser Zahl ist der Umkreis der Objekte, auf die der Begriff sinngemäß Anwendung findet, kleiner oder größer. Bezeichnet man den Inbegriff der Merkmale eines Begriffes als dessen Inhalt, so den Inbegriff der Arten (Unterarten, bzw. Exemplare), auf die der Begriff sich bezieht, als seinen Umfang, sein Anwendungsgebiet oder auch, wie neuerdings vorgeschlagen worden ist, sein Geltungsbereich (Riehl). Der Umfang des Begriffes ist keine Zahlengröße; er wird nicht dadurch vermehrt oder vermindert, daß es eines der unter ihm gedachten Objekte mehr oder weniger auf der Welt gibt; er ist vielmehr eine logische Größe die — in funktionaler Abhängigkeit von der Größe des Inhalts stehend — dadurch größer oder kleiner wird, daß der Begriff seinem Inhalt nach auf einen größeren oder kleineren Umkreis von Objekten bezogen werden muß.
Die Beziehungen zwischen dem Inhalt und dem Umfang eines Begriffes lassen sich leicht an der Hand eines Beispiels ableiten. Determiniert man etwa den Begriff „Uhr“ durch das Merkmal der besonderen[S. 27] Herstellungsweise seines Gegenstandes, so wird dadurch sein Inhalt reicher, sein Umfang ärmer; determiniert man den so gewonnenen Begriff (Ankeruhr, Pendeluhr usw.) etwa durch die Angabe des Materials, aus dem der Gegenstand gebildet ist (Gold, Silber, Stahl usw.), so wird abermals der Inhalt reicher, der Umfang ärmer. Setzt man das fort, so findet man stets, daß mit der Bereicherung des Inhalts (Determination) der Umfang vermindert; mit der Verringerung des Inhalts (im Gegensatz zur Determination das Verfahren der Abstraktion) der Umfang vermehrt wird. Für das Verhältnis von Inhalt und Umfang eines Begriffes ergibt sich danach das logische Gesetz, daß der Umfang — als vom Inhalt abhängige Größe — um so ärmer ist, je reicher der Inhalt, und umgekehrt um so reicher, je ärmer der Inhalt.
Inhalt und Umfang haben in ihrer Größe sowohl nach oben wie nach unten hin Grenzen. Da ein Begriff ohne Inhalt nicht denkbar ist, so bildet ein einziges konstituierendes Merkmal den kleinsten Inhalt eines Begriffes. Diese inhaltsärmsten Begriffe mit nur einem einzigen konstituierenden Merkmal haben den größten Umfang. Also: der Umfang eines Begriffes kann nie größer werden, als wenn sein Inhalt bei dem Minimum „ein Merkmal“ angekommen ist. Und umgekehrt: die Begriffe mit dem ärmsten Umfang, also diejenigen, die sich nur noch auf einen einzigen raum-zeitlich bestimmten Gegenstand beziehen (z. B. auf die blaue Grotte bei Capri in dem Augenblicke ihrer Entdeckung durch Kopisch im Jahre 1826; auf Cäsar im Augenblicke seiner Ermordung; auf den ersten geschichtlich bekannten Ausbruch des Vesuvs im Jahre 79 v. Chr.) haben den reichsten Inhalt, den ein Begriff haben kann. Dem ärmsten Inhalt (= 1) entspricht demnach der reichste Umfang; dem ärmsten Umfang (= 1) der reichste Inhalt. Oder: zwischen Inhalt und Umfang eines Begriffes besteht eine Beziehung, die wir in einer Formel ausgedrückt schreiben können: 1maximum = maximum1, wobei 1 = minimum ist.
Für die Einteilung der Begriffe können mehrfache Gesichtspunkte in Betracht kommen. Wenn wir Begriffe mit nur einem einzigen Merkmale einfache nennen, dann können Begriffe, deren Inhalt aus einer Mehrheit von Merkmalen besteht (ungeachtet ihrer Einheitlichkeit[S. 28] als Begriffsformen), zusammengesetzte heißen. Ein Begriff nähert sich also der Einfachheit durch Abstraktion, wird dagegen um so zusammengesetzter, je mehr man ihn determiniert. Zusammengesetzte Begriffe sind nach der Art ihrer Zusammensetzung entweder möglich oder unmöglich. Das unterscheidet sie von Vorstellungen und Urteilen. Vorstellungen sind wirklich oder nichtwirklich; Urteile wahr oder falsch; Begriffe allein sind möglich oder unmöglich (Verwandtes bei J. Geyser). Mögliche Begriffe sind solche, deren Inhalt aus miteinander verträglichen Merkmalen, unmögliche solche, deren Inhalt aus miteinander unverträglichen Merkmalen zusammengesetzt ist. Da nun die Merkmale, die den Inhalt eines Begriffes bilden, selbst wiederum Begriffe sind, die einen bestimmten Inhalt haben, so sind damit auch die Begriffe in miteinander verträgliche und unverträgliche eingeteilt. Unverträgliche Begriffe sind z. B. alle, wie man sagt, kontradiktorisch-entgegengesetzten Begriffe, das sind solche, deren einer ausschließt, was in dem Inhalt des anderen gedacht ist (z. B. schön und nichtschön; frei und nichtfrei; Sklave und Nichtsklave). Dabei nennt man schön und frei wohl auch positive, nichtschön und nichtfrei negative, unfrei und unschön limitative (privative) Begriffe, obschon die letzteren nur ihrer Form, nicht ihrem Inhalt nach von den negativen abweichen. Ein aus kontradiktorisch-entgegengesetzten Merkmalen zusammengesetzter Begriff bildet eine sog. „contradictio in adiecto“ (zu deutsch: „Widerspruch im Beiwort“; z. B. „nichtfremder Fremdling“, „unbekannter Bekannter“). Eine „contradictio in adiecto“ kann auch zustande kommen durch die Verbindung zweier sog. konträr-entgegengesetzter Merkmale im Inhalt eines Begriffes. Konträr-entgegengesetzte Begriffe sind solche, deren Inhalt gegensätzliche Bestimmungen enthält, die sich zumeist einander ausschließen, ohne daß sie sich aber immer einander ausschließen müßten (z. B. schön und häßlich; hoch und niedrig; gut und schlecht; links und rechts; gesund und krank; Mann und Weib). Der Begriff „schwarzer Schimmel“ bildet eine „contradictio in adiecto“, weil das Merkmal „schwarz“ das in „Schimmel“ gedachte wesentliche Merkmal „weiß“ ausschließt. Analoges gilt für Begriffe wie „weißer Neger“, „viereckiger Kreis“, „rundes Quadrat“. Wohl aber sind Begriffe wie „guter Bösewicht“, „reitender Fußgänger“, „wacher Träumer“ gelegentlich möglich, weil ein Bösewicht eben unter Umständen auch[S. 29] einmal gut, ein Fußgänger auch einmal reiten, ein Träumer auch einmal wach sein kann. Zu den unmöglichen Begriffen gehören schließlich diejenigen, in denen durch Determination ein Merkmal hinzugefügt wird, das schon im Stammbegriff selbst als wesentlich enthalten ist (z. B. „weißer Schimmel“, „toter Leichnam“, „kahle Glatze“, „alter Greis“).
Mit dem Vorstehenden ist die Einteilung der Begriffe noch nicht beschlossen. Der Begriff „Körper“ ist, wie man sagt, nach seinen konstitutiven Merkmalen Gattungsbegriff gegenüber den verschiedenen Arten der Körper (feste, flüssige, gasförmige); diese wiederum sind Artbegriffe gegenüber jenem. Begriffe stehen also nach der Beschaffenheit ihres Inhalts (und demzufolge auch ihres Umfangs) zueinander in dem Verhältnis der Über- und Unter- sowie der Nebenordnung. Gattungsbegriffe sind ihren Artbegriffen übergeordnet; Artbegriffe ihrem Gattungsbegriffe untergeordnet; Artbegriffe einer und derselben Gattung sind einander nebengeordnet. Hierzu kommt noch eine weitere Scheidung: die in Individual- und Kollektivbegriffe. Individual- (oder Einzel-) begriffe sind solche, deren Gegenstand ein nicht mehr in Arten einzuteilendes Individuum ist (z. B. Helmholtz, Gaurisankar, Madrid, Schlacht an der Lorettohöhe im Mai 1915). Diese sind wiederum entweder allgemeine (Gesamtbegriffe), wenn in ihnen das Individuum schlechthin und ganz im allgemeinen gedacht ist; oder spezielle (Spezialbegriffe), wofern in ihnen das Individuum raum-zeitlich oder wie sonst immer speziell bestimmt gedacht ist. So umfaßt der Gesamtbegriff „Napoleon“ eine Reihe von Spezialbegriffen, wie z. B.: Napoleon als Knabe, als Feldherr, als Kaiser, als Gatte und Vater, als Schriftsteller, als Verbannter u. a. m. Kollektivbegriffe sind demgegenüber solche, deren Gegenstand durch die Zusammenfassung einer Anzahl von Gegenständen zu einem Gegenstand gebildet ist (so z. B. häufig durch die Zusammenfassung von Merkmalen, die bestimmten Gattungen oder Arten gemeinsam sind). Beispiele dafür sind: Staat; Papsttum; Schönheit; Reichtum; Menschheit; Weisheit; Religiosität; Freiheit.
Die Unterschiede der Über- und Unterordnung haben nur relativen Charakter: ein und derselbe Begriff kann seinem übergeordneten gegenüber Art, seinem untergeordneten gegenüber Gattung sein. Nur die Einzelbegriffe, in welche die Artbegriffe allmählich durch immer zunehmende Determinierung ihres Inhaltes auslaufen, sind[S. 30] frei von dieser Relativität. Sie bleiben als Individualbegriffe allen höheren Arten und Gattungen untergeordnet und können nicht mehr zu Art- oder Gattungsbegriffen selbst werden. Das gleiche gilt im umgekehrten Sinne von den höchsten Begriffen, also denen, die den ärmsten Inhalt und weitesten Umfang haben: sie bleiben gegenüber allen anderen Begriffen immer Gattungen, weil es ihnen gegenüber keine höheren Gattungen mehr gibt.
Über das Verhältnis von Gattungs- und Artbegriffen lassen sich unter Hinzunahme der oben dargestellten Beziehungen zwischen Inhalt und Umfang der Begriffe leicht folgende Tatsachen ableiten: Gattungsbegriffe haben gegenüber ihren Artbegriffen einen ärmeren Inhalt, aber reicheren Umfang; Artbegriffe haben gegenüber ihrem Gattungsbegriffe einen reicheren Inhalt, aber ärmeren Umfang. Die Bestimmungen, um die der konstituierende Inhalt eines Artbegriffes reicher ist als der seines Gattungsbegriffes, gehören dem Inhalt des Gattungsbegriffes bereits als mögliche Merkmale an; denn ein Gattungsbegriff wird zum Artbegriff nur durch Determinierung seines Inhalts, und die Merkmale, durch die man ihn determiniert, müssen ihm folglich schon vordem als mögliche Merkmale zugehören. Der Inhalt eines Gattungsbegriffes umfaßt die seinen Arten gemeinsamen wesentlichen Merkmale, unter Abstraktion von den nichtgemeinsamen, die in den Arten, wie man zu sagen pflegt, die „artbildenden Unterschiede“ (differentiae specificae) bilden. Der Umfang eines Gattungsbegriffes ist gleich dem Inbegriff der Umfänge aller seiner Arten. Der Umfang eines Artbegriffes deckt sich also mit einem Teil des Umfangs seines Gattungsbegriffes und ist selbst gleich dem Inbegriff der Umfänge aller der ihm untergeordneten Arten (Unterarten oder Individuen). Artbegriffe sind ihrem Gattungsbegriffe unmittelbar untergeordnet; die Individuen dieser Arten ebendemselben Gattungsbegriffe mittelbar; und ebenso: Gattungsbegriffe sind ihren Arten unmittelbar, den Individuen dieser Arten mittelbar übergeordnet.
Durch die Beziehungen der Über- und Unterordnung schließen sich die Begriffe miteinander zu Reihen zusammen, in denen man von immer inhaltsärmeren und umfangsreicheren zu immer inhaltsreicheren und umfangsärmeren Begriffen hinauf- und hinabsteigen kann. Nennen wir den Inbegriff aller in solchem Verhältnis zueinander stehender Begriffe eine Ordnungsreihe des Denkens, so ergibt sich, daß wir die Begriffe noch in solche gleicher und verschiedener Ordnungen scheiden können. Aber auch diese Scheidung ist nur in relativem Sinne gültig; denn nach oben laufen ja die Ordnungsreihen des Denkens durch immer höhere Gattungsbegriffe mehr und mehr zusammen, um schließlich in einer höchsten gleichwie gearteten Spitze zu enden. Nach unten gehen sie im Gegensatz dazu in immer breitere Verzweigungen auseinander, die sich mit zunehmender Determinierung[S. 31] immer mehr verästeln. Diese Verzweigungen darf man sich nun nicht etwa als voneinander getrennte und streng geschiedene vorstellen. Man muß sie vielmehr so versinnbildlichen, daß sie einander beständig kreuzen, ineinander übergehen und miteinander in mannigfach verschlungene Beziehungen treten. Ein und derselbe Begriff kann entsprechend seinem Inhalt verschiedenen Ordnungsreihen angehören, je nach dem Gesichtspunkte, von dem aus man ihn zum Gliede einer Einteilung macht, und bildet damit allemal einen Kreuzungspunkt, an dem die Reihen ineinander überfließen.
Das Ganze der menschlichen Begriffe bildet also ein anschaulich kaum zu versinnbildlichendes System, in dem die untere Grenze durch jene Begriffe gebildet wird, in denen wir bei dem reichsten Inhalt und dem ärmsten Umfang gewisse raumzeitlich bestimmte individuelle Gegenstände denken (z. B. Cäsar im Augenblicke seiner Ermordung, die Zerstörung des Tempels zu Jerusalem im Jahre 70 n. Chr. Geb., den Abbruch der diplomatischen Verhandlungen zwischen Österreich-Ungarn und Serbien am 25. Juli 1914). Ihnen gegenüber stehen an der Spitze aller Begriffe die sog. Kategorien (oberste Denkformen), die bei dem ärmsten Inhalt den größten Umfang haben. Das Wort „Kategorien“ (zu deutsch: Aussageformen) stammt von Aristoteles, der in seinen logischen Schriften zehn solcher höchsten Begriffe aufzählt, und zwar: „Substanz, Quantität, Qualität, Relation, Raum, Zeit, Lage, haben, tun, leiden“. Demgegenüber versuchen bereits die Stoiker eine Verbesserung, indem sie erklären, der höchste Begriff sei der des „etwas überhaupt“; dieser wiederum zerfalle in vier Unterabteilungen, die da sind: „Substanz oder Ding, notwendige Eigenschaft, unwesentliche Beschaffenheit, Beziehung“. Kant stellt zwölf Kategorien auf, und zwar als Kategorien der Quantität: Einheit, Vielheit, Allheit; als Kategorien der Qualität: Realität, Negation, Einschränkung; als Kategorien der Relation: Substanz, Ursache, Gemeinschaft; als Kategorien der Modalität: Möglichkeit, Dasein und Notwendigkeit; während Schopenhauer glaubt, alle Kategorien auf eine einzige, auf die der Kausalität, reduzieren zu können. — In der neueren Logik werden zumeist drei Arten oberster Begriffe angenommen, und zwar am häufigsten: 1. Begriffe von Dingen (Substanzen) als dem selbständigen Sein; 2. Begriffe von Eigenschaften einschließlich Zuständen und Veränderungen (Akzidentien) als dem unselbständigen Sein oder Sein in einem anderen;[S. 32] 3. Begriffe von Beziehungen (Relationen) als den Verhältnissen, die zwischen mindestens zwei Dingen, Eigenschaften oder Beziehungen durch Unterscheidung und Vergleichung gedacht werden. Damit ist gesagt: alle Begriffe, in denen wir denken, sind entweder Ding-, Eigenschafts- oder Beziehungsbegriffe, haben also zu Gegenständen entweder Dinge oder Eigenschaften (bzw. Zustände und Veränderungen) oder Beziehungen. Demgegenüber darf aber nicht übersehen werden, daß diese drei Kategorien wiederum unter einer höheren Gattung zusammenfallen, worauf bereits die Stoiker, neuerdings Hamilton, aufmerksam gemacht haben: unter der des Gegenstandes oder des Seienden überhaupt. Alle Begriffe sind — insofern etwas in ihnen gedacht werden muß, wenn sie mit Recht diesen Namen tragen sollen — Begriffe von einem Etwas überhaupt oder, wie wir dafür sagen wollen, Begriffe von Gegenständen überhaupt. Die Gegenstände zerfallen dann in die obersten Arten der Dinge, Eigenschaften und Beziehungen.
[4] So schon Aristoteles in seinem Satze: „οὐδέποτε ἄνευ φαντάσματος ἡ ψυχὴ νοεῖ“ (niemals denkt die Seele ohne Vorstellungen).
[5] Zur Orientierung sei empfohlen: Joseph Geyser, Einführung in die Psychologie der Denkvorgänge, Paderborn 1909, ferner: N. Braunshausen, Einführung in die experimentelle Psychologie (ANuG Bd. 484); E. v. Aster, Einführung in die Psychologie (ANuG Bd. 492).
Alles Denken ist in seinem weitesten Sinne Urteilen oder Fragen. (Das Schließen ist keine selbständige Art des Denkens, sondern, wie sich zeigen wird, eine Art des Urteilens, und zwar ein mittelbares oder vermitteltes Urteilen im Gegensatz zum unmittelbaren.) Der Frage gegenüber ist das Urteil das Ursprünglichere; denn die Frage hat, wie zu erörtern sein wird, ihrer logischen Beschaffenheit nach das Urteil zur Voraussetzung. Die traditionelle Logik hat die Bedeutung der Frage für das Denken und ihr Verhältnis zum Urteil im allgemeinen stiefmütterlich behandelt. Das soll hier vermieden werden; indessen setzt die logische Analyse der Frage die des Urteils voraus und muß darum zweckmäßig an den Schluß der Urteilslehre gestellt werden.
Urteilen heißt, um es zunächst allgemein zu sagen, von einem Gegenstande als logischem Subjekt etwas aussagen, was diesem — sei es eine Eigenschaft (Zustand, Veränderung) oder eine Beziehung — als logisches Prädikat zukommt. In dieser Beziehung zwischen dem Gegenstand der Aussage (Subjekt = S) und der eigentlichen Aussage selbst (Prädikat = P) liegt das Wesen des Urteils; sie macht seinen Charakter aus und bedingt seine Verschiedenheit von anderen[S. 33] Faktoren des Seelenlebens, von Vorstellungen und Begriffen. Vorstellungen — seien es solche der Wahrnehmung, Erinnerung oder Einbildung — sind, wie schon in anderem Zusammenhange betont, wirklich oder nichtwirklich; Begriffe sind der Zusammensetzung ihres Inhalts nach möglich oder nichtmöglich; Urteile allein sind wahr oder falsch. Wahrheit und Falschheit sind also kennzeichnende Eigentümlichkeiten, die von allen Produkten unseres Seelenlebens allein dem Urteil zukommen.
Die traditionelle Logik pflegt für die Einteilung der Urteile das von Kant im Anschluß an scholastische Unterscheidungen entworfene Schema zugrunde zu legen, das besagt: Urteile sind der Quantität nach: allgemeine (alle S sind P) oder besondere (einige S sind P) oder einzelne (S ist P); der Qualität nach: bejahende (S ist P) oder verneinende (S ist nicht P) oder unendliche (S ist non-P); der Relation nach: kategorische (S ist P) oder hypothetische (wenn Q R, dann S P) oder disjunktive (S ist entweder P oder P1); der Modalität nach: problematische (S kann P sein) oder assertorische (S ist tatsächlich P) oder apodiktische (S muß P sein)[6]. Dieses Schema hat indessen durch die neuere Logik (so schon durch Schopenhauer, durch Herbart) so zahlreiche Umgestaltungen erfahren, daß es auch hier in veränderter Fassung zugrunde gelegt werden darf.
Urteile sind nach ihrem Bestande entweder einfache oder zusammengesetzte; nach ihrer Beziehung auf das Wirkliche entweder Real- oder Idealurteile. Einfache Urteile sind solche, deren Analyse nur ein Subjekt und ein Prädikat; zusammengesetzte solche, deren Analyse entweder mehrere Subjekte oder mehrere Prädikate, im ganzen also mehrere einfache Urteile als Glieder des Bestandes ergibt. Realurteile sind solche, in denen wir die ausgesagte Beziehung als vom Denken unabhängig wirklich, Idealurteile solche, in denen wir diese nur im Gedachtwerden wirklich voraussetzen. Von den[S. 34] Idealurteilen kommen für die logische Analyse vor allem die mathematischen und logischen Urteile in Betracht. Diese sollen als Urteile über die Beziehungen zwischen Formen und Größen Formalurteile heißen, im Gegensatz zu den Realurteilen als Urteilen über die Vorgänge und Beziehungen der Wirklichkeit (daher: Wirklichkeitsurteile, Tatsachenurteile). Die Scheidung der Urteile in Real- und Idealurteile wird erst in einem späteren Zusammenhange Bedeutung gewinnen; die in einfache und zusammengesetzte ist bereits hier wichtig.
Für die logische Gliederung der Urteile nach Gattungen und Arten ist die Einteilung der einfachen Urteile grundlegend; sie gilt mittelbar auch für die zusammengesetzten, insofern als diese ja aus einfachen Urteilen gebildet sind. Die einfachen Urteile sind nach der Inhaltsbestimmung ihres Subjektsbegriffes entweder Subjekt-unbestimmte, auch Impersonalien genannt (z. B. „es regnet, es klopft“) oder Subjekt-bestimmte (S ist P); die Subjekt-bestimmten Urteile wieder nach der Beschaffenheit ihres Subjekts entweder Gattungs- oder Einzel- (generelle oder individuelle) Urteile, nach der Beschaffenheit ihres Prädikats entweder Inhärenz- oder Relationsurteile. Inhärenzurteile sind ferner entweder Qualitätsurteile (z. B. „Die Bienen sammeln Honig“) oder klassifikatorische (z. B. „Bienen sind Insekten“) oder normative Urteile (z. B. „Du sollst lernen“); Relationsurteile sind entweder quantitative oder qualitative (S ist größer, schöner als P) sowie entweder kausale (S bewirkt P) oder existentiale (S existiert). In einem Schema angeordnet sieht demnach die Einteilung der einfachen Urteile folgendermaßen aus:
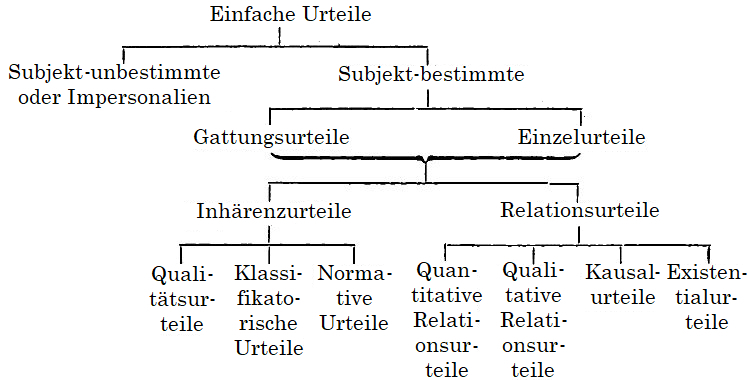
[S. 35]
Die zusammengesetzten Urteile sind je nach der Art ihrer Zusammensetzung entweder Beurteilungen oder Urteilsverbindungen oder Urteilsgefüge. Beurteilungen — auf der Grenze der zusammengesetzten Urteile zu den einfachen stehend — sind solche Aussagen, deren Subjekt selbst wieder ein Urteil ist. Sie zerfallen in die Arten der verneinenden (S ist nicht P), quantitativ- und modal-bestimmenden Urteile; die zu zweit genannten wieder in universale und partikuläre (alle S sind P; einige S sind P); die zuletzt genannten in apodiktische, assertorische und problematische Behauptungen (S ist notwendig, tatsächlich, möglicherweise P). Urteilsverbindungen sind solche zusammengesetzte Urteile, in denen mehrere einfache Urteile entweder kopulativ (S1 und S2 sind P) oder konjunktiv (S ist P1 und P2) oder divisiv (S ist teils P1, teils P2) miteinander verknüpft sind. Urteilsgefüge endlich sind Urteilszusammensetzungen, in denen eine Mehrheit von Urteilen in eine entweder ausschließende oder begründende Beziehung zueinander gerückt sind; die ersteren (S ist entweder P1 oder P2) heißen disjunktive, die letzteren (wenn Q R, dann S P) hypothetische Urteilsgefüge. Verdeutlichen wir die Arten der zusammengesetzten Urteile gleichfalls an Hand eines Schemas, dann ergibt sich:
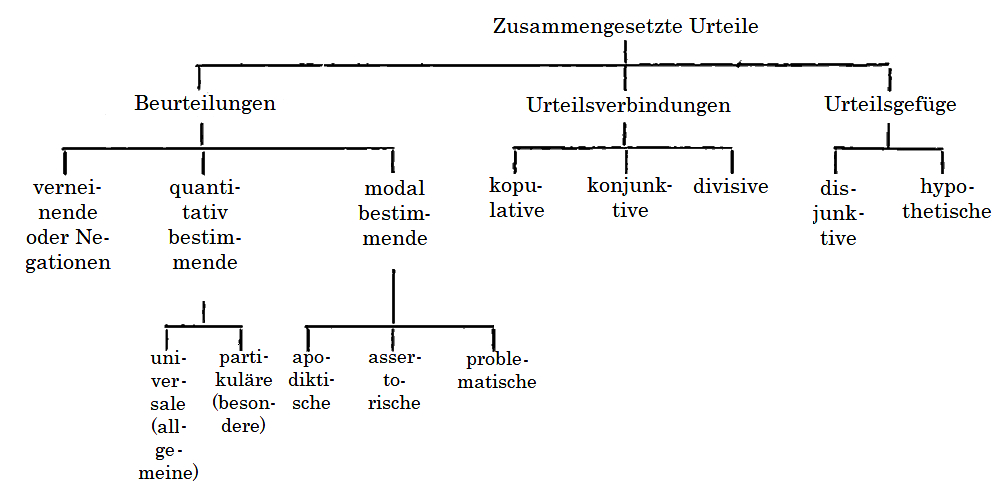
Die logische Analyse des Urteils legt ihrer Untersuchung das elementare bejahende Urteil von der Form „S ist P“ zugrunde. Was für dieses als gültig erwiesen ist, muß mutatis mutandis auch für die noch[S. 36] so kompliziert zusammengesetzten Urteile gelten, da jene aus diesen gebildet sind.
Das Urteil verhält sich zum Satz wie der Begriff zum Worte, mit dem er verbunden ist. Der Satz ist also mehr als die äußere Hülle des Urteils; er ist Träger, Vermittler des im Urteil enthaltenen Gedankens, wie das Wort Träger, Vermittler des mit ihm verknüpften Begriffes ist. Nichtsdestoweniger ist zwischen der grammatischen Analyse des Satzes und der logischen Analyse des Urteils ein strenger Unterschied zu ziehen. Grammatisch mag ein Satz auch aus noch so vielen Bestandteilen zusammengesetzt sein (Subjekt, Prädikat, Objekt, näheren Bestimmungen des Ortes, der Zeit usw. als grammatischen Kategorien); logisch sind alle Urteile zweigliedrig (so schon Beneke; auch Wundt, Erdmann, Geyser). Nur eine grammatisierende Logik, (welche die Logik entweder mit der Grammatik identifiziert oder beider Grenzen durcheinanderfließen läßt), vermag die Annahme zu vertreten, daß ein Urteil logisch mehr oder weniger als zwei Glieder haben könne. Und nur eine psychologisierende Logik vermag der grammatisierenden darin beizupflichten, indem sie nämlich die psychologische Frage nach dem Vorstellungsbestande des Urteilens der logischen Frage nach dem Aufbau des Urteils substituiert. In dem elementaren Urteil: „S ist P“ ist „S“ grammatisch Subjekt, „ist“ Kopula und „P“ Prädikat oder Objekt; logisch dagegen „S“ Subjekt und das „P-sein des S“ Prädikat. Mögen wir von hier aus auch zu den grammatisch verwickeltsten Urteilsformen aufsteigen, logisch wird sich allemal zeigen, daß sie nur aus zwei Gliedern bestehen: dem Subjekt als dem Gegenstand, über den, und dem Prädikat, als dem Gegenstand, der ausgesagt wird.
| logisches Subjekt: | logisches Prädikat: |
| ↓ | ↓ |
| ein Knabe | starb |
| ein siebenjähriger Knabe |
starb nach kurzer Krankheit
|
| ein siebenjähriger blonder Knabe |
starb nach kurzer Krankheit in den Armen seiner
Mutter
|
| ein siebenjähriger blonder Knabe, der sich beim Baden erkältet hatte |
starb nach kurzer Krankheit in den Armen seiner Mutter an einer
Lungenentzündung
|
[S. 37]
Das gleiche gilt auch, obwohl es gelegentlich bestritten worden ist, für die sog. „verkürzten Urteile“ oder „Urteilsworte“ (z. B. „komm“, „bleibe“, „Hilfe!“, „stirb“), deren logischer Sinn soviel ist wie „ich will, daß du kommst“, „ich will, daß du bleibst, hilfst“ usw., wobei „ich“ logisches Subjekt, „will, daß du kommst“ logisches Prädikat ist. Noch an Hand einer anderen Art von Urteilen hat man versucht, die Zweigliedrigkeit der Urteile in Zweifel zu ziehen, und zwar an der Hand der Subjekt-unbestimmten Urteile oder Impersonalien. Inwiefern auch hier der erhobene Einwand haltlos ist, wird sich zeigen, wenn von dieser Urteilsart im speziellen die Rede sein wird.
Damit ist für die Frage nach dem Wesen des Urteils zunächst so viel gewonnen, daß jedes Urteil seinem logischen Aufbau nach aus zwei materialen Gliedern bestehe, die im Urteilsakt in eine bestimmte Beziehung zueinander gerückt werden. Diese Beziehung zwischen Subjekt und Prädikat, d. i. die eigentlich prädikative (aussagende) Beziehung oder Form des Urteils ihrem Wesen nach zu bestimmen, ist die weitere Aufgabe der logischen Analyse des Urteils.
Sieht man von allen Besonderheiten psychologisierender oder grammatisierender Urteilstheorien ab[7], so kann man die bisher entwickelten Auffassungen in zwei Gruppen scheiden. Die eine glaubt, die Inhalts-, die andere die Umfangsbeziehungen zwischen dem Subjekts- und dem Prädikatsbegriff als die für die Theorie des Urteils maßgebenden betrachten zu müssen. Die ersteren werden danach als Inhaltstheorien, die zweiten als Umfangstheorien bezeichnet. Der Gegensatz dieser Auffassungen ist ein so weit reichender, daß sich im Anschluß daran geradezu von verschiedenen Richtungen der Logik sprechen läßt, deren eine als Inhaltslogik, deren andere als Umfangslogik anzusprechen ist.
Zu den Umfangstheorien gehört die älteste und verbreitetste Annahme über das Wesen des Urteils, die sog. Subsumtionstheorie (vertreten durch Aristoteles, Lambert, Kant, Hegel). Sie deutet die Urteilsbeziehung zwischen Subjekt und Prädikat so, daß der Umfang des Subjektsbegriffes unter den Umfang des Prädikatsbegriffes subsumiert sei. Das Subjekt werde also als Art zu dem Prädikat als Gattung gedacht. In dem Urteil „Kunst bringt Gunst“ z. B. sei „das Gunst-bringende“ Gattungsbegriff gegenüber dem[S. 38] Begriff „Kunst“ als einer seiner Arten; „die Kunst“ mithin unter den Begriff „Gunst-bringendes“ subsumiert. — Dieser Theorie verwandt ist eine zweite, die sog. Identitätstheorie des Umfangs (vertreten z. B. durch Ploucquet; in reiferer Form durch W. Hamilton in der sog. Lehre von der Quantifikation des Prädikats und deren Anhängern Thompson, de Morgan). Ihr zufolge seien im Urteil Subjekts- und Prädikatsbegriff ihrem Umfang nach als gleich groß (identisch) gedacht. In der Behauptung „Alle Rosen tragen Dornen“ sei der Umfang des Begriffes „Dornen-tragendes“ nicht größer als der des Begriffes „alle Rosen“; denn der Subjektsbegriff „alle Rosen“ schränke den sonst weiteren Umfang des Begriffes „Dornen-tragendes“ auf seinen eigenen Umfang ein. Das Urteil müsse genau genommen also heißen: „Alle Rosen sind dornentragende Rosen.“ — Als Vertreter der Umfangslogik kommen neben den Genannten auch alle Anhänger der mathematischen Logik in Betracht. Diese deuten das Urteil sowohl im Sinne der Subsumtions- wie der Identitätstheorie des Umfangs, wobei die Inhaltsbeziehungen völlig verloren gehen. Sie schreiben in mathematischem Gewande für Urteile wie „Kochsalz ist Chlornatrium“: „S = P“, für Urteile wie „Silber ist ein Metall“: „S ( P“, indem sie die Gleichheitsbeziehungen des Umfangs durch =, die Subsumtionsbeziehungen durch ( wiedergeben. Nehme man beide Symbole zusammen, dann lasse sich das Wesen des Urteils darstellen durch den Ausdruck: S ( P. — Von den Inhaltstheorien sei hier nur die sog. Identitätstheorie des Inhalts erwähnt (vertreten durch H. St. Jevons, in anderer Gestalt durch Lotze). Nach ihr sei das Wesen des Urteils darin zu suchen, daß in ihm Subjekt und Prädikat als inhaltsgleich (inhaltsidentisch) gedacht werde. Die Behauptung: „Ein Teil der Menschen ist farbenblind“ bedeute mithin soviel wie: „Einige Menschen (unter denen jedoch nur die Farbenblinden zu verstehen sind) sind farbenblinde Menschen.“ — (Ausführliche Darstellung und Kritik dieser Urteilstheorien bei B. Erdmann, Logik I2, Kap. 43.)
Für die Bestimmung des Wesens des Urteils ist zunächst davon auszugehen, daß sowohl dem Subjekts- wie dem Prädikatsbegriff ein Inhalt und ein Umfang zukommt, die im Urteil zueinander in eine bestimmte logische Beziehung treten. Wie aber schon die Lehre vom Begriff zeigte, daß der Umfang eine vom Inhalt abhängige Größe sei, so ergibt auch die Analyse des Urteils, daß die Umfangsbeziehungen eine Folge der Inhaltsbeziehungen, diese mithin die primären und für die Theorie des Urteils maßgebenden sind. Darüber, ob zwei Begriffe miteinander in das Verhältnis von Subjekt und Prädikat treten können, entscheiden nicht die Beziehungen ihres Umfangs, sondern ihres Inhalts. Die Begriffe „Gold“ und „Metall“ haben nur darum einen Teil ihres Umfangs gemeinsam, weil sie einen Teil ihrer konstituierenden Merkmale gemeinsam haben, dergestalt, daß „Gold“ zur Art gegenüber der Gattung „Metall“ wird. Daß sie also miteinander zu dem Urteil „Gold ist ein Metall“ zusammentreten[S. 39] können, hängt von der Beschaffenheit ihrer Merkmale, mithin ihres Inhalts, nicht von der ihres Umfangs ab.
Die sich daraus ergebende Auffassung des Urteils erweist sich mithin als eine Inhaltstheorie. Die Frage, vor der die logische Analyse nunmehr steht, lautet: Welcher Art sind im Urteil die Inhaltsbeziehungen zwischen Subjekts- und Prädikatsbegriff?
Der Erörterung dieser Frage seien drei elementare Urteile von der Form „S ist P“ zugrunde gelegt: 1. Atome (im Sinne der Lehre Demokrits) sind unteilbar; 2. ebene Dreiecke sind Flächen, die von drei geraden Linien begrenzt werden; 3. der brave Mann denkt an sich selbst zuletzt. Nehmen wir das erste dieser Urteile, so erweist sich der Prädikatsbegriff „unteilbar“ als ein notwendiges Merkmal des Subjektsbegriffes „Atom“. Alle Merkmale des Unteilbaren sind also in dem Inhalt des Begriffes „Atom“ enthalten. Der Inhalt des Subjektsbegriffes „Atom“ ist aber reicher als der des Prädikats. „Unteilbar“ kann als Merkmal auch dem Unkörperlichen zukommen; das Atom dagegen ist gerade dadurch gekennzeichnet, daß es körperlich, d. h. ausgedehnt ist. Der Inhalt des Prädikatsbegriffes verhält sich also zu dem des Subjektsbegriffes so, daß er mit einem Teil dieses identisch ist; und die Beziehung zwischen Subjekts- und Prädikatsinhalt ergibt sich als eine Beziehung unvollständiger Gleichheit. Nehmen wir das zweite Urteil: „Ebene Dreiecke sind Flächen, die von drei geraden Linien begrenzt werden.“ In diesem enthält das Prädikat alle notwendigen Merkmale, die dem Subjektsbegriff zukommen, mit anderen Worten: es definiert diesen. Nicht im Prädikat enthalten, obschon daraus ableitbar, sind dagegen alle möglichen Merkmale des Subjekts, die dessen Inhalt im weiteren Sinne bilden. Auch hier also herrscht die Beziehung vor, daß der Prädikatsbegriff mit einem Teil des Gesamtinhalts des Subjektsbegriffes (und zwar mit dem Inhalt im engeren Sinne) identisch ist, abermals eine Beziehung unvollständiger Gleichheit. Ebendasselbe ergibt sich an Hand des dritten Beispiels: „Der brave Mann denkt an sich selbst zuletzt.“ In diesem ist das Prädikat ein abgeleitetes oder mögliches Merkmal des Subjektsbegriffes; es hat also zu diesem die Beziehung, daß es mit einem Teil von dessen Inhalt (und zwar mit einem Teil des Inhalts im weiteren Sinne) identisch ist, wiederum also wie oben die Beziehung unvollständiger Gleichheit. Sehen wir von den Differenzen dieser drei Beziehungsarten ab, dann muß das Verhältnis unvollständiger[S. 40] Inhaltsgleichheit zwischen Subjekts- und Prädikatsbegriff als ein dem Urteil eigentümliches anerkannt werden.
Die Frage nach dem Wesen des Urteils ist damit aber nicht gelöst. Auch zwei nicht im Urteil aufeinander bezogene Begriffe können miteinander in dem Verhältnis unvollständiger Inhaltsgleichheit stehen, nämlich dann, wenn sie einen Teil ihrer Merkmale gemeinsam haben (z. B. Kranich und Vogel [gemeinsam alle Merkmale des Vogels]; Empfindung und Atom [gemeinsam das Merkmal der Einfachheit]; Schimmel und Schnee [gemeinsam das Merkmal des Weißen]). Was unterscheidet die Beziehung unvollständiger Inhaltsgleichheit im Urteil von dieser vom Urteil unabhängigen? — Die Antwort auf diese Frage hat davon auszugehen, daß in jedem Urteil der Prädikatsbegriff den Subjektsbegriff in und vermöge jener unvollständigen Gleichheit ihrer Inhalte determiniert. Wann und wie wir auch urteilen, immer hat die Beziehung zwischen Subjekt und Prädikat den Zweck, den Inhalt des Subjekts für den vorliegenden Fall um den Inhalt des Prädikats zu bereichern. Einen Begriff um ein Merkmal „bereichern“ heißt dabei: ihn so denken, daß sein Inhalt den Inhalt jenes Merkmals in sich enthält, wobei notwendige Merkmale notwendige bleiben, mögliche zu wirklichen werden. Heiße der Begriff, der determiniert wird, „S“, der, durch welchen determiniert wird, „P“, so bedeutet die Determination des „S“ durch „P“ soviel wie: „P ist in S enthalten“ oder: „P bildet einen Teil des Inhalts von S“. Alle Determination von Begriffen erfolgt also durch Urteile, und Urteilen ist selbst nichts anderes als Determinieren. Die Begriffsbildung als Vorgang der Determination setzt mithin das Urteilen voraus; oder, wie schon früher betont: Urteile, nicht Begriffe, sind die Formelemente des Denkens. Kurz gesagt: Zu der Beziehung unvollständiger Inhaltsgleichheit zwischen zwei Begriffen kommt im Urteil noch das hinzu, daß der Subjektsbegriff durch das Prädikat determiniert wird; oder: der Inhalt des Prädikatsbegriffes ist nicht nur einem Teile des Subjektsinhaltes gleich, sondern er bildet selbst diesen Teil. Er ist mithin dem Subjektsinhalt logisch immanent oder auch, wie wir dafür sagen können: er ist vermöge des Urteilsgedankens diesem logisch eingeordnet. Damit ergibt sich als Wesen des Urteils die Einordnung des Prädikats- in den Subjektsinhalt; als Theorie des Urteils eine Einordnungstheorie, wie wir sie im Anschluß an die Namengebung ihres Begründers B. Erdmann[S. 41] (vgl. Logik I2, S. 358 f.) nennen wollen. Drücken wir die Einordnungsbeziehung zwischen Subjekt und Prädikat symbolisierend durch einen Pfeil aus, dann können wir als Form des elementaren Urteils schreiben: „S ← P“, wobei die Pfeilrichtung andeutet, daß das „P“ dem „S“ eingeordnet ist, nicht umgekehrt[8].
Daraus ergibt sich, daß das Urteil keine Verbindung oder Trennung von Begriffen, keine Zerlegung eines Begriffes in seine Teilbestimmungen ist, sondern vielmehr das eigentümliche logische Verhältnis zweier Begriffe, durch das der Inhalt des einen (Prädikat) als ein Teil des Inhalts des anderen (Subjekt) gedacht wird. Die vermeintliche analysierende Trennung von Subjekt und Prädikat als Voraussetzung des Urteils und ihre im Urteil selbst erfolgende Ineinssetzung ist also kein logischer, sondern lediglich ein sprachlicher Vorgang, dem gewisse, für die Logik bedeutungslose psychologische Funktionen vorangehen. Begriff und Urteil sind nichts prinzipiell voneinander Verschiedenes. In und mit jedem Begriff denken wir einen bestimmten Inhalt, dem ein ganzer Inbegriff von Merkmalen, in und mit jedem Urteil einen Inhalt, dem dieses oder jenes bestimmte Merkmal logisch immanent ist. Begriffe sind mithin sozusagen kristallisierte Urteile, Urteile sich bildende Begriffe. Mögliche Begriffe entsprechen formal-gültigen, unmögliche formal-ungültigen Urteilen.
Nach dem Gesagten dürfen die Ausführungen über die Umfangsbeziehungen zwischen Subjekt und Prädikat, die sich aus der Beziehung der Einordnung ergeben, kurz sein. Bildet das Prädikat einen Teil des Subjektsinhaltes, so kann sein Umfang — als der eines Gliedes im Urteil — nicht kleiner und nicht größer sein als der des Subjekts. Die Umfangsbeziehungen sind mithin die der Identität, wobei der Prädikatsbegriff vom Subjekt, nicht dieses von jenem abhängt. „Gold ist ein Metall“ bedeutet soviel wie: alle Merkmale des Begriffes „Metall“ kommen dem Begriff „Gold“ zu und gelten dementsprechend von dem gesamten Umfang, von dem der Begriff „Gold“ gilt. Jede Einschränkung des Subjektsumfanges (z. B. im partikulären Urteil „einige S ← P“) schränkt also entsprechend auch den Umfang des Prädikats ein; denn dieses wird vom Subjekt nur soweit als gültig ausgesagt, wie das Subjekt selbst seinem Umfang nach Anwendung findet.
Alle Urteile — (sofern wir von dem in der Lüge enthaltenen Spezialfall beabsichtigter Täuschung absehen) — sind psychologisch[S. 42] mit dem Bewußtsein der Wahrheit verbunden (Gewißheit; Überzeugtheit; Geltungsbewußtsein; Glaube; englisch = belief) und erheben den Anspruch darauf, von anderen als wahr angenommen zu werden. Das Denken ist seinem Wesen und Ziel nach wahres Denken, und wo es dieses Ziel nicht erreicht, da hat es seinen ihm ursprünglich eigenen Zweck verfehlt.
Wahr nennen wir Urteile, wenn sie sowohl ihrer Form wie ihrem Inhalt nach gültig, unwahr (oder falsch), wenn sie entweder ihrer Form oder ihrem Inhalt nach ungültig sind. An jedem Urteil also läßt sich wie zwischen Form und Inhalt so auch zwischen formaler und materialer Gültigkeit unterscheiden. Die formale Gültigkeit betrifft die logische Beziehung zwischen Subjekt und Prädikat; die materiale die materialen Urteilsglieder, d. h. den Subjekts- und Prädikatsbegriff selbst. Ein Urteil wie: „Voltaire telegraphierte von Berlin nach Potsdam ...“ ist formal gültig, aber material ungültig, weil es einen Anachronismus enthält, daher falsch. Das Urteil: „Die Leiche erhebt sich und spricht ...“ ist bereits formal ungültig, weil sein Prädikat dem konstituierenden Inhalt seines Subjektes widerspricht, mithin auch material ungültig, also falsch. Daraus ergibt sich, daß Urteile material ungültig und doch formal gültig sein können — (nur für die mathematischen Urteile fällt formale und materiale Gültigkeit zusammen); daß aber umgekehrt Urteile nicht formal ungültig sein können, ohne es auch material zu sein. Die Bedingungen der formalen Gültigkeit der Urteile sind mithin zugleich mittelbare Bedingungen ihrer materialen Gültigkeit; die Bedingungen der materialen Gültigkeit nicht aber solche der formalen.
Besteht das Wesen des Urteils in der Einordnung des Prädikats in den Subjektsinhalt, so können wir als erste vornehmlichste Bedingung der formalen Gültigkeit eines Urteils die aufstellen, daß einem Subjekt als Prädikat nur eingeordnet werden darf, was mit den Merkmalen, die seinen konstituierenden Inhalt bilden, verträglich ist. Das Subjekt also entscheidet darüber, was von ihm ausgesagt werden kann und was nicht. Urteile sind demnach formal ungültig, mithin falsch, wenn ihr Prädikat dem konstituierenden Inhalt des Subjektsbegriffes irgendwie widerspricht. Diese Bedingung stellt den allgemeinen logischen Grundsatz der Prädikation dar, den wir kurz formulieren können: „Keinem Subjekt kann als Prädikat[S. 43] zukommen, was seinem konstituierenden Inhalt irgendwie widerspricht.“
Dem allgemeinen Grundsatz der Prädikation nahe verwandt ist eine zweite formale Bedingung der Urteilsgültigkeit, die besagt, daß einem und demselben Subjekt in mehreren Urteilen nur solche Merkmale als Prädikate eingeordnet werden dürfen, die einander nicht ausschließen. Nehmen wir hinzu, daß solche Begriffe, deren einer ausschließt, was in dem anderen als wesentlich gedacht ist, kontradiktorisch-entgegengesetzte heißen, dann können wir im Sinne dieser Bedingung auch schreiben: „Einem und demselben Subjekt dürfen in mehreren Urteilen nicht einander kontradiktorisch-entgegengesetzte Bestimmungen als Prädikate eingeordnet werden.“ Die Formulierung dieser Bedingung bezeichnet die traditionelle Logik als logischen Grundsatz des Widerspruches. Schon Aristoteles hat ihn als ersten und gewissesten Grundsatz der Gültigkeit der Urteile erkannt und ihn in den Worten zum Ausdruck gebracht: „Es ist unmöglich, daß etwas ebendemselben unter den gleichen Voraussetzungen zukomme und auch nicht zukomme.“ Leibniz erwähnt ihn in der Monadologie; Wolff gibt ihm die Fassung: „Es kann etwas nicht zugleich sein und auch nicht sein.“ In der neueren Logik hat er eine wechselvolle Geschichte gehabt, die bisher nicht geschrieben ist. Erdmann formuliert ihn: „Es ist undenkbar, daß dasselbe demselben unter denselben Voraussetzungen zukomme und auch nicht zukomme.“
An der Hand des logischen Grundsatzes des Widerspruches läßt sich ein dritter formaler Grundsatz der Urteilsgültigkeit leicht ableiten. Von den beiden Urteilen der Form „S ← P“ und „S ← nicht-P“ ist gesagt worden, daß sie als einander ausschließend nicht zugleich gültig sein können. Eine geringe Überlegung lehrt weiter, daß, wo eines dieser Urteile gültig ist, das andere ungültig sein muß. Überall also, wo von einem und demselben Subjekt in mehreren Urteilen kontradiktorisch-entgegengesetzte Bestimmungen ausgesagt werden, ist, wenn eines dieser Urteile gültig, das andere notwendig ungültig und umgekehrt. Eine dritte Möglichkeit gibt es nicht; das folgt aus der Natur unseres Denkens ebenso unmittelbar, wie daß 2 × 2 = 4 und nicht = nicht-4 ist. Die traditionelle Logik nennt diesen Satz den logischen Grundsatz vom ausgeschlossenen Dritten. Wir können ihn kurz aussprechen in der Form: „Wenn von zwei Urteilen, deren eines bejaht, was das andere verneint, eines als wahr gegeben ist, dann ist[S. 44] notwendig das andere falsch und umgekehrt“; oder: „Wenn von zwei Urteilen mit einem und demselben Subjekt, aber einander kontradiktorisch-entgegengesetzten Prädikaten eines wahr ist, dann ist notwendig das andere falsch und umgekehrt.“ — (Auch dieser Grundsatz, zuerst aufgestellt von Aristoteles in mehreren abweichenden Formulierungen, hat in der Geschichte der Logik mannigfach wechselnde Auffassungen gefunden, die ihn zum Streitobjekt gemacht haben. Die vorstehend entwickelte Fassung lehnt sich dem Inhalt nach an die von Erdmann gegebene an.)
Wenden wir uns zu den Bedingungen der materialen Gültigkeit der Urteile, dann können wir fürs erste festlegen: „Urteile sind material gültig, wenn ihr Inhalt als unmittelbar gewiß einleuchtet“ (logischer Grundsatz der unmittelbaren Gewißheit). Daß es solche Urteile gibt, hat bereits Aristoteles erkannt (Lehre von den unbeweisbaren Wahrheiten). Descartes und Locke nennen sie intuitive Erkenntnisse, weil sie sich dem Verstande unmittelbar als gültig aufdrängen. Ein kennzeichnendes Merkmal besteht für sie allemal in der Denkwidrigkeit ihres kontradiktorischen Gegenteils. Das Urteil: „Gleiches zu Gleichem addiert gibt Gleiches“ ist unmittelbar-gewiß für jeden, der den Sinn der Worte versteht; denn sein kontradiktorisches Gegenteil ist ebenso unmittelbar jedem als ungültig bewußt. Die unmittelbar-gewissen Urteile sind daher für alles menschliche Denken notwendige und allgemeingültige Wahrheiten. Beispiele für sie finden sich besonders unter den Urteilen der Mathematik und Logik, also den Formalurteilen, und werden gemeinhin als Axiome (Grundsätze) bezeichnet. Hierhin gehören der logische und mathematische Grundsatz der Identität (als mathematischer Satz: „Jede Größe ist sich selbst gleich“); der Grundsatz der Drittengleichheit („Sind zwei Größen einer dritten gleich, so sind sie untereinander gleich“); das Geradenaxiom („Zwischen zwei Punkten ist die Gerade der kürzeste Weg“); das sog. Parallelenaxiom („Durch einen Punkt läßt sich in einer Ebene zu einer Geraden nur eine Parallele ziehen“); der allgemeine logische Grundsatz der Prädikation; die logischen Grundsätze des Widerspruches, vom ausgeschlossenen Dritten, der unmittelbaren Gewißheit u. a. m.
Von den unmittelbar-gewissen Urteilen zu scheiden ist eine zweite Gruppe der Formalurteile, die wir — als aus den unmittelbar-gewissen notwendig abgeleitete — mit dem Namen „mittelbar-gewisse Urteile“[S. 45] bezeichnen wollen. Bilden die unmittelbar- und mittelbar-gewissen Urteile zusammen das Reich der Gewißheit (Verstandeswahrheiten, Vernunftwahrheiten; bei Leibniz: „vérités de raison“), so steht diesen ein zweites Reich von Urteilen gegenüber, das der Erfahrung. Erfahrungsurteile (Wirklichkeitsurteile, Tatsachenurteile; bei Leibniz: „vérités de fait“) sind solche, deren materiale Glieder irgendwie unmittelbar oder mittelbar dem Bestande der Wahrnehmung oder Erinnerung entnommen sind, wobei als Arten der Wahrnehmung vom logischen Standpunkte aus die eigene und die fremde (mitgeteilte, überlieferte, geschichtliche) Wahrnehmung zu unterscheiden sind. Mittelbar-gewisse und Erfahrungsurteile haben nun miteinander gemeinsam, daß sie als Bedingung ihrer materialen Gültigkeit einer zureichenden Begründung bedürfen. Diese Bedingung können wir — als logischen Grundsatz der zureichenden Begründung — formulieren: „Jedes Urteil, das nicht unmittelbar gewiß ist, bedarf zum Erweise seiner materialen Gültigkeit einer zureichenden Begründung.“ Die spezielle Art der zureichenden Begründung von mittelbar-gewissen und Tatsachenurteilen ist entsprechend dem Unterschiede dieser Urteilsarten verschieden. Geht bei den mittelbar gewissen die Begründung als deduktive Ableitung auf Urteile intuitiver Gewißheit sowie auf letzte Definitionen zurück (ableitende Begründung), so besteht sie bei den Erfahrungsurteilen entweder geradesweges in dem Hinweis auf die Daten der Wahrnehmung (hinweisende Begründung), oder sie stützt sich — ob als deduktive, induktive oder analogiemäßige Ableitung — letzten Endes doch immer auf solche Urteile, deren Begründung nicht anders als hinweisend gegeben werden kann. Spezielles darüber kann sich erst in der Lehre vom Schlußverfahren sowie in der Methodenlehre ergeben.
Auch der logische Grundsatz der zureichenden Begründung hat eine weit zurückreichende Geschichte. Angedeutet bei Plato und Aristoteles, wird er zuerst von Leibniz als „Gesetz des zureichenden oder bestimmenden Grundes“ („loi de la raison suffisante ou déterminante“) ausdrücklich formuliert und als logisches Prinzip der Tatsachenwahrheiten dem Satz des Widerspruches als dem logischen Prinzip der Vernunftwahrheiten gegenüberstellt. Leibniz aber wie sein gelehriger Schüler Christian Wolff vermengen noch den logischen Grundsatz der zureichenden Begründung mit dem allgemeinen Kausalgesetz (welches besagt, daß nichts, was geschieht, ohne zureichende Ursachen ist, durch die es geschieht), eine Unzulänglichkeit der logischen Analyse, die bereits von Crusius, ebenso von Kant bemerkt, nichtsdestoweniger aber erst im neunzehnten Jahrhundert (Schopenhauer) endgültig überwunden worden ist.
[S. 46]
Logisches Subjekt eines Urteils ist dasjenige Glied, von dem ausgesagt, genauer: dem nach der Immanenz des Prädikats im Subjekt ein Merkmal inhaltlich eingeordnet ist. Mag das Subjekt sprachlich — nach dem Bestande der Worte, durch die es im Satze formuliert ist — noch so zusammengesetzt sein, ja mag es grammatisch selbst in einem vollständigen Satze bestehen: logisch ist es als Subjekt der Aussage eine Einheit. Der Subjektsbegriff bildet den Gegenstand der Aussage; dieser wiederum kann nach dem kategorialen Bestande des Denkens ein Ding, eine Eigenschaft (einschließlich Zuständen und Veränderungen) oder auch eine Beziehung sein. Der Subjektsbegriff ist mithin entweder ein Ding-, ein Eigenschafts- oder ein Beziehungsbegriff. Auch da, wo das logische Subjekt des Urteils selbst wieder in einem Urteil besteht (z. B. bei den sog. „Beurteilungen“), bleibt es begrifflich eine Einheit, der wie allen Begriffen nur ein Inhalt zukommt, zu dem das Prädikat in der Urteilsbeziehung der Einordnung gedacht ist.
Urteile sind als Subjekt-bestimmte nach der Beschaffenheit dieses Subjekts entweder Gattungs- (generelle) oder Einzel- (individuelle) Urteile. Beispiele der ersteren sind alle diejenigen, deren Subjekt ein Gattungsbegriff („Der Wolf ist ein Raubtier“), Beispiele der letzteren alle diejenigen, deren Subjekt ein Einzel- — sei es ein Gesamt- oder Spezialbegriff — ist („Goethe hat ein hohes Alter erreicht“).
Zu dieser Einteilung pflegt man in der traditionellen Logik (seit Aristoteles und Apulejus) noch eine weitere hinzuzufügen, d. i. die Scheidung der Urteile nach ihrer Quantität in allgemeine (universale) und besondere (partikuläre) (alle, einige S ← P). Der Versuch einer Deutung dieser Urteilsarten bildet eines der umstrittensten logischen Probleme. Sigwart hat die Theorie aufgestellt, daß die Quantitätsbestimmung in den Urteilen „einige, alle S ← P“ nicht ein zum Subjekt gehöriges logisches Attribut, sondern vielmehr das Prädikat des Urteils sei (Prädikatstheorie der quantitativen Bestimmung des Subjekts). Der Sinn des Urteils „alle S ← P“ sei soviel wie: „die S, die P sind, sind alle S“; der Sinn des Urteils „einige S ← P“ soviel wie: „die S, die P sind, sind einige S“. Diese Auffassung hat[S. 47] zahlreiche Anhänger gefunden (u. a. Riehl). — Demgegenüber hat B. Erdmann treffend darauf hingewiesen, es sei unerfindlich, warum die Sprache, die sonst so logisch zu Werke gehe, diese Verdrehung vornehme. Habe das Urteil „alle S ← P“ den Sinn: „die S, die P sind, sind alle S“, dann sei das scheinbare Prädikat „P“ nicht Prädikat, sondern ein von vornherein zum Subjekt gehöriges logisches Attribut und die Umfangsbestimmung des Subjekts (alle, einige) — scheinbar Attribut des Subjekts — das Prädikat. Überprüfe man aber den Sachverhalt, so ergebe sich, daß die beiden Urteile „alle S ← P“ und „einige S ← P“ sich nicht durch ihr Prädikat, sondern durch ihr Subjekt unterscheiden. In beiden werde ein und dasselbe Prädikat „P“ einmal dem Subjekt „alle S“, das anderemal dem Subjekt „einige S“ eingeordnet. Die Quantitätsbestimmung „alle — einige“ habe demnach als quantitatives Attribut des Subjekts keine prinzipiell andere logische Funktion wie etwa die qualitativen Attribute „schön, gut, häßlich“ (Attributstheorie der quantitativen Bestimmung des Subjekts). Die quantitativ bestimmten Urteile seien mithin als Umfangsurteile von den nicht quantitativ bestimmten — den Gattungs- und Einzelurteilen — als Inhaltsurteilen zu scheiden (vgl. B. Erdmann, Logik I2, S. 468 ff.).
Demgegenüber ließe sich nun darauf hinweisen, daß die quantitativen Bestimmungen „alle, einige“ nicht in ebendemselben Sinne Inhaltsbestimmungen des Subjekts bilden können wie die qualitativen Attribute „schön, häßlich“, weil sie ja nicht auf den Inhalt, sondern auf den Umfang des Begriffes gehen. Auch ist offenbar die Annahme von Umfangsurteilen schwer mit der Theorie des Urteils in Einklang zu bringen, die, wie wir sahen, als Einordnungstheorie zu den Inhaltstheorien des Urteils gehört. Aus diesen Schwierigkeiten führt die dritte und letzte Theorie heraus, die darum hier vertreten sei. Nach dieser sind die universalen und partikulären Urteile nicht Urteile schlechthin, sondern Beurteilungen, und zwar quantitativ bestimmende Beurteilungen. Der Sinn der Aussage: „Alle S ← P“ ist soviel wie: das Urteil S ← P gilt für alle S; der Sinn des Urteils „einige S ← P“ soviel wie: das Urteil S ← P gilt für einige S (Beurteilungstheorie der quantitativen Bestimmung des Subjekts). Aus diesem Grunde gehört die Besprechung der universalen und partikulären Urteile nicht in den vorstehenden Zusammenhang, sondern erst zu dem Abschnitt über Beurteilungen.
[S. 48]
Die bisherigen Ausführungen über das Subjektsglied des Urteils beziehen sich durchgehends auf jene Art von Aussagen, die wir als Subjekt-bestimmte bezeichnet haben. Von ihnen unterscheiden wir nun diejenigen Urteile, denen zwar das Subjekt — wie man vielfach angenommen hat, so Herbart (Lehrb. z. Einl. i. d. Phil. 5. A. § 63) — nicht fehlt, bei denen es aber inhaltlich unbestimmt gelassen ist. Die traditionelle Logik hat diese Urteile nicht sehr kennzeichnend „Impersonalien“ genannt (so auch Sigwart); andere — mit dieser Namengebung nicht zufrieden — haben sie ganz unzutreffend als „subjektslose Sätze“ gedeutet (Miklosisch, Marty). Glücklicher ist demgegenüber die Bezeichnung von B. Erdmann, der „Prädikatsurteile“ vorschlägt. Aber auch diese Benennung ist hier nicht gewählt worden: denn sie benutzt als Gesichtspunkt der Namengebung nicht, was die vorliegende Art der Urteile von anderen scheidet, sondern was sie mit anderen gemeinsam hat. Besteht das Wesen dieser Urteile darin, daß sie das logische Subjekt, also das Glied, von dem ausgesagt wird, inhaltlich unbestimmt lassen, so nennen wir sie zweckmäßig „Subjekt-unbestimmte Urteile“.
Mit der Wahl des Namens ist gleichzeitig eine Theorie dieses Urteils gegeben. Der entwickelten Lehre, daß alle Urteile zweigliedrig seien, widersprechen die Subjekt-unbestimmten Aussagen nicht nur nicht, sondern sie bestätigen sie gerade. Betrachten wir eine Reihe dieser Urteile, so finden wir, daß in fast allen der Inhalt der Aussage in einem Vorgang oder in einer Veränderung besteht, die von dem Urteilenden wahrgenommen wird, ohne daß ihm die Ursache und damit das Subjekt dieser Veränderung bekannt wäre. Aussagend formuliert er dann: „es regnet, es schneit, es wetterleuchtet, es wird Frühling.“ Das menschliche Denken kann, wo es Vorgänge findet, deren Ursachen ihm unbekannt bleiben, nicht umhin, diesen Vorgängen zureichende Ursachen zugrunde zu legen, als deren Wirkungen es diese deutet. Es urteilt in solchen Fällen, indem es das Subjekt der Aussage unbestimmt läßt. Nur die dichtende Phantasie der Volksseele sprengt bisweilen diese Fessel der Unwissenheit; dann entstehen Urteile wie: „Gott läßt regnen, Frau Holle schüttelt die Federn aus“ oder auch, wenn es gewittert: „Gott zürnt, grollt, schilt“. Subjekt-unbestimmte Urteile sind demnach gemeinhin Aussagen über Vorgänge der Wahrnehmung, deren Ursachen unbekannt, aber als existierend vorausgesetzt werden. Insofern diese Vorgänge stets als Wirkungen unbekannter[S. 49] Ursachen gefaßt werden, sind die Subjekt-unbestimmten Urteile eine Art der Kausalurteile (über die erst an späterer Stelle zu sprechen sein wird), und zwar der Beschaffenheit ihres Subjekts nach unbestimmte Kausalurteile (vgl. B. Erdmann, Logik I2, S. 435 ff.).
Als Arten der Subjekt-unbestimmten Urteile können wir einmal solche mit meteorologischem und chronologischem Inhalt; das andere Mal solche unterscheiden, die auf unvollständigen Wahrnehmungen der Sinne oder der Selbstbeobachtung beruhen, wie sie das tägliche Leben zahlreich nahelegt. Als Beispiele der ersteren seien genannt: „es regnet, es schneit, es blitzt, es donnert“ (meteorologischer Inhalt); „es ist spät, es ist 7 Uhr, es ist Nacht, es wird Morgen, es ist Herbst, es ist Feiertag, es ist zwei Jahre her“ (chronologischer Inhalt). Als Beispiele der letzteren: „es klopft, es klingelt, es raschelt, es spukt“ (Sinneswahrnehmung); „es geht gut, es geht schlecht, es friert mich, es hungert mich, es juckt, es brennt, es reut mich, es gelüstet mich“ (Selbstwahrnehmung).
Logisches Prädikat eines Urteils ist dasjenige Glied, welches ausgesagt, genauer: welches dem Inhalt des Subjektbegriffes logisch eingeordnet ist. Auch das Prädikat kann logisch mannigfach zusammengesetzt, grammatisch aus mehreren Worten und Wortverbindungen bestehen: in seiner Eigenschaft als Prädikat nach dem Wesen der Urteilsfunktion ist es eine Einheit, eben der eigentlich aussagende Bestandteil des Urteils.
In jedem Urteil sind Subjekt und Prädikat zueinander in eine Beziehung gerückt, die wir oben als die logische Beziehung der Einordnung erkannt haben. Darum sind aber nicht alle Urteile gleich Beziehungsurteile, d. h. solche, die von ihrem Subjekt irgendwelche Beziehungen aussagen. Die Arten der Prädizierungen lassen sich vielmehr in zwei große Gruppen teilen, die wiederum in verschiedene Unterarten zerfallen. Wird von einem Subjekt als Gegenstand des Urteils etwas ausgesagt, was diesem als inneres Merkmal zugehört, ihm also inhäriert, wie das Akzidenz der Substanz, so haben wir ein Urteil der ersten Gruppe, der sog. Inhärenzurteile; wird von einem Subjekt als Gegenstand des Urteils irgendeine Beziehung zu einem anderen Gegenstande ausgesagt, dergestalt, daß beide Gegenstände als selbständige, zum mindesten trennbare gedacht und als solche voneinander unterschieden und miteinander verglichen werden, so haben wir ein Urteil der zweiten Gruppe, der sog. Relationsurteile.[S. 50] Als Arten der Inhärenzurteile unterscheiden wir die Qualitäts-, die klassifikatorischen und die normativen Urteile; als Arten der Relationsurteile die Aussagen über quantitative, qualitative und kausale Beziehungen, sowie über Existenz und Nichtexistenz.
Besprechen wir zunächst die Arten der Inhärenzurteile. Qualitätsurteile sind solche, in denen von dem Subjekt eine Eigenschaft (ein Zustand oder eine Veränderung) ausgesagt wird. Beispiele dafür sind: „die Blätter des Efeus sind grün; der Mohr hat seine Arbeit getan; die Glocken läuten; veni, vidi, vici“. Das Prädikat des Qualitätsurteils kann sowohl eine Eigenschaft im engeren Sinne wie auch eine Größen- oder Maßbestimmung sein („der Schnee ist weiß; Körper sind dreidimensional“). Ebenso können die Eigenschaften als dem Gegenstand der Aussage objektiv zugehörig gedacht oder auch lediglich als subjektive Wertschätzung des Urteilenden ausgesagt werden. Das Urteil: „die Kuppel des Berliner Domes ist vergoldet“ ist ein objektives; das Urteil: „der Vortrag war ergreifend schön“ ein subjektives Qualitätsurteil oder, wie man für die letzteren sagt, ein Werturteil. Tätigkeiten oder Zustände werden von Gegenständen ausgesagt, um diese entweder als wirkend oder leidend zu kennzeichnen. Schließlich können Qualitätsurteile auch zeitlich- und räumlich-individualisierende Bestimmungen haben (Angaben des Wann, Wo, Unter-welchen-Umständen usw.).
Klassifikatorische Urteile sind solche, in denen das Prädikat eine Bestimmung über den logischen Ort des Subjekts in den Ordnungsreihen des Denkens enthält. Das klassifikatorische Urteil „Zink ist ein Metall“ besagt soviel wie: Zink ist eine der Arten der Gattung Metall; als solcher kommen ihr alle die Merkmale zu, die dem Gattungsbegriff Metall zukommen. Das gleiche gilt analog für alle klassifikatorischen Urteile. Beispiele solcher sind: „Der Mensch ist ein Säugetier; H2SO₄ ist eine Schwefelwasserstoffverbindung; Geld ist ein Tauschmittel; das ist eine Gänseblume“. — Kurz hingewiesen sei hier auf das Verhältnis der klassifikatorischen Urteile zu den Definitionen der Wissenschaften, über die erst in der Methodenlehre zu sprechen sein wird. Von den beiden Arten zu definieren, der genetischen und systematischen Definition, kommt hier nur die letzte in Frage. Das systematische Definitionsurteil bestimmt (gleich dem klassifikatorischen Urteil) den logischen Ort des Subjekts in den Ordnungsreihen des Denkens, indem es den nächsthöheren Gattungsbegriff angibt; aber[S. 51] es geht in seinem Prädikat weiter als dieses, indem es dazu noch die spezifischen Unterschiede hinzufügt, durch welche die zu definierende Art sich von anderen Arten der gleichen Gattung abhebt. Das Urteil: „Dreiecke sind ebene Flächen“ ist ein klassifikatorisches; das Urteil: „Dreiecke sind ebene Flächen, die von drei geraden Linien eingeschlossen werden“ eine systematische Definition. Insofern kann das klassifikatorische Urteil sehr wohl als eine Vorstufe der systematischen Definition betrachtet werden.
Etwas mühsamer als bei den Qualitäts- und klassifikatorischen Urteilen gestaltet sich die logische Analyse bei den sog. normativen Urteilen. Beispiele dieser sind: „Der Herr sei Herr, der Diener diene; im Schweiße deines Angesichts sollst du dein Brot verdienen; bete und arbeite; fiat iustitia, pereat mundus“. In ihnen ist nicht wie in den eben besprochenen Arten der Inhärenzurteile eine Seinsbestimmung von dem Subjekt ausgesagt, sondern ein Sollen, ein Wunsch, eine Aufforderung, ein Befehl, eine Bitte des Urteilenden enthalten. Aber das Fehlen dieser Seinsbestimmung ist nur scheinbar. Der Imperativ ist logisch immer die Form des „ich will“. In der Bitte Wallensteins: „Max, bleibe bei mir, geh nicht von mir, Max“ ist Subjekt des Urteils der Urteilende, genauer der Bittende selbst, Prädikat seine Bitte bzw. sein Wunsch. Das gilt für alle normativen Urteile. Sie enthalten ebenso eine Seinsbestimmung wie die anderen Arten der Inhärenzurteile. Subjekt ist in ihnen der Bittende, Befehlende, Wünschende selbst. Wo dieses kein reales Wesen ist, wie in ethischen Geboten und Gesetzen („Du sollst nicht töten, du sollst nicht ehebrechen“), da ist es in idealen Faktoren zu suchen wie: Humanität, Recht, Sitte, Anstand oder auch: Gott, Religion, Tradition u. a. m.
In diesem Zusammenhange soll kurz der sog. Benennungsurteile gedacht werden. Schon ein beliebiges Beispiel (etwa das Urteil: „Nennen wir diese Art von Aussagen, die das Subjekt unbestimmt lassen, Subjekt-unbestimmte Urteile“) lehrt, daß es sich hier um eine normative Urteilsform handelt. Das gegebene Beispiel enthält eine Aufforderung, in der der Urteilende etwa sagt: „ich schlage vor, diese Art von Urteilen usw. ... zu nennen“. Das gilt für alle diejenigen Benennungsurteile, die einen Vorschlag, also die Empfehlung einer Namensgebung, enthalten. Anders verhält es sich mit denjenigen Urteilen, die nicht eine bestimmte Benennung vorschlagen, sondern lediglich deren Vorhandensein aussagen. Urteile wie: „Die Griechen bezeichnen den Zustand reiner, ungetrübter innerer Zufriedenheit als „εὐφρωσύνη“ oder: „Die Hebräer nannten die Stätte der Toten das Scheol“ oder: „Aussagen dieser[S. 52] Art heißen Inhärenzurteile“ sind keine normativen, sondern Qualitätsurteile, die besagen, wie dieser oder jener etwas bezeichnet oder bezeichnet hat, bzw. wie dieser oder jener Gegenstand heißt oder bezeichnet worden ist.
Kommen wir zu den Relationsurteilen. Quantitative Relationsurteile sind solche, deren Prädikat besagt, in welchem Verhältnis des Raumes, der Zeit, der Zahl, des Maßes, des Grades usw. der Gegenstand der Aussage zu einem anderen Gegenstande steht. Beispiele dieser Urteile sind: „Der Außenwinkel an der Spitze eines gleichschenkligen Dreiecks ist doppelt so groß wie jeder der beiden Basiswinkel; Schiller ist zehn Jahre später geboren als Goethe und dreißig als Lessing; Erziehungsfähigkeit ist ein höherer Grad der Gelehrigkeit“. Alle diese Urteile setzen ein Unterscheiden und Vergleichen zweier Gegenstände voraus, über deren Gleichheit oder Verschiedenheit in bezug auf Raum, Zeit, Zahl, Maß und Grad sie eine Bestimmung enthalten. Als einfachste Form der Relationsurteile mögen sie die Grundlage bilden für die allgemeinen Bestimmungen über das Wesen der Relationsbehauptungen überhaupt.
Alle Relationsurteile setzen zwei Gegenstände voraus, die voneinander unterschieden und miteinander verglichen werden. Alle Relationsurteile ferner sind korrelativer Natur; d. h.: die Beziehung, in die in ihnen die beiden Gegenstände (Beziehungsglieder) gerückt sind, gilt in entsprechendem Sinne auch umgekehrt. Ist A größer als B, dann ist B kleiner als A; ist A zahlreicher als B, dann ist B an Zahl geringer als A. Als Urteil entspricht das Relationsurteil der oben entwickelten Theorie des Urteils vollständig. Es ist fürs erste logisch zweigliedrig. Nehmen wir das Beispiel: „Ein schneller Tod ist besser als langes Siechtum“, so ist darin Subjekt: „ein schneller Tod“, Prädikat: „das Bessersein (des Todes) als ein langes Siechtum“. Und die Beziehung zwischen Subjekt und Prädikat ist auch hier die der Einordnung des Prädikats- in den Inhalt des Subjektsbegriffes.
Diese allgemeinen Bestimmungen über das Wesen der Relationsurteile finden sich bei allen ihren Arten bestätigt. Qualitative Relationsurteile sind solche, deren Prädikat besagt, in welchem Verhältnis qualitativer (nicht quantitativer) Gleichheit, Ähnlichkeit oder Verschiedenheit der Gegenstand der Aussage zu einem anderen steht. Beispiele solcher Urteile sind: „Beethovens neunte Symphonie ist die weitaus großartigste unter seinen Symphonien; die Luft in den Großstädten ist morgens reiner als abends; du bist wie eine Blume,[S. 53] so hold, so schön, so rein; Napoleon Bonaparte hat einige verwandte Züge mit Alexander dem Großen.“ Wie wir oben subjektive und objektive Qualitätsurteile unterschieden, so sind auch die qualitativen Relationsurteile in subjektive und objektive zu teilen. Ein subjektives Relationsurteil ist z. B. ein Urteil wie: „Das Leben ist wertvoller als der Tod; aber das sündhafte Leben ist wertloser als dieser“ (Wertrelationsurteil); ein objektives Relationsurteil: „Die Farbe der Eichenblätter ist heller als die der Kastanienblätter.“ Der korrelative Charakter der qualitativen Relationsurteile ist leicht ersichtlich. Das Urteil: „Geben macht seliger denn Nehmen“ gilt auch entsprechend in der Fassung: „Nehmen macht weniger selig als Geben“.
Die kausalen Relationsurteile bedürfen gleichfalls nur kurzer Besprechung. Beispiele dieser sind: „Steter Tropfen höhlt den Stein; viele Köche verderben den Brei; allzu scharf macht schartig; Adam und Eva wurden von Gott aus dem Paradiese vertrieben.“ Kausale Relationsurteile sind also solche, in denen entweder das Subjekt als Ursache irgendeines Vorganges oder irgendein Vorgang als Wirkungsweise einer im Prädikat bezeichneten Ursache gefaßt wird. Auf das erkenntnistheoretische Kausalproblem (die Frage, ob und inwieweit das menschliche Denken berechtigt sei, gewisse Vorgänge, die ihm nur als zeitlich regelmäßig folgende gegeben sind, in die Beziehung von Ursache und Wirkung zueinander zu setzen) soll hier nicht eingegangen werden[9]. Für die Logik genügt es festzustellen, daß das menschliche Denken, einem ihm innewohnenden Zwange gehorchend, nicht umhin kann, Vorgänge, die immer zusammen oder als einander folgende wahrgenommen sind (z. B. den Eintritt des Todes nach dem Genuß vergifteter Speisen; das Auftreten von Erschöpfungszuständen nach größeren Arbeitsleistungen), als durch das Verhältnis von Ursache und Wirkung verbunden aufzufassen. Ein ursachloses Geschehen ist ihm undenkbar. Alles, was geschieht, hat vielmehr zureichende Ursachen, durch die es geschieht; das gilt für die psychische Welt ebenso wie für die physische (Grundsatz der Kausalität). Auch Kausalurteile sind entsprechend der oben gegebenen Bestimmung korrelativen Charakters. Ist A die Ursache von B, dann ist B die Wirkung von A. Oder an Hand eines Beispiels: „Kain erschlug Abel“ ist inhaltsgleich[S. 54] mit „Abel wurde von Kain erschlagen“. Daß die sog. „Impersonalien“ kausale Relationsurteile sind, ist bereits oben erwähnt worden. Sie bilden Aussagen über einen (entweder gegenwärtigen oder erinnerten oder eingebildeten) Vorgang, der als Wirkung einer unbekannten Ursache gedacht und so prädiziert wird, daß das Subjekt logisch unbestimmt bleibt. Wir nannten sie aus diesem Grunde: Subjekt-unbestimmte kausale Relationsurteile.
Zu den Relationsurteilen gehört endlich eine letzte Art von Urteilen, deren Prädikat von ihrem Subjekt lediglich besagt, daß es Existenz habe (sog. Existentialurteile). Beispiele dafür sind: „Es war einmal eine Prinzessin; wahrlich, es gibt noch gerechte Richter; es gibt schwarze Schwäne; es gibt irrationale Zahlen; es gibt einen Gott; ich, der ich denke, existiere“. Der Urteilscharakter dieser Behauptungen steht fürs erste außer Frage. Zweifelhaft könnte dagegen sein, ob es sich hier um eine Art der Relationsurteile handelt. Denn es ist zunächst nicht ohne weiteres ersichtlich, welches der Beziehungspunkt ist, zu dem das Subjekt, von dem im Urteil die Existenz behauptet wird, in Relation gestellt wird. Eine geringe Überlegung lehrt jedoch, daß das allemal der Urteilende selbst ist. Die Gegenstände, deren Existenz wir aussagen, sind entweder ideale, d. h. solche, denen wir Existenz nur im Denken oder Vorstellen beimessen; oder reale, d. h. solche, die wir als unabhängig vom Vorstellen und Denken existierend voraussetzen. Die letzteren sind als Subjekte von Existentialurteilen entweder Gegenstände der Wahrnehmung oder Gegenstände möglicher Wahrnehmung oder auch nach Analogie der Gegenstände möglicher Wahrnehmung gedachte Gegenstände. Demnach heißt urteilen, daß ein solcher Gegenstand Existenz habe, entweder soviel wie urteilen, daß er in der Wahrnehmung gegenwärtig sei; oder daß er Gegenstand der Wahrnehmung werden könnte, wenn man ihn aufsuchte; oder auch, daß er nach Analogie der Gegenstände möglicher Wahrnehmung gedacht werden müsse. Damit ist der korrelative Charakter der Existentialurteile erwiesen. Bedeuten die Aussagen über Existenz, daß der Gegenstand des Urteils als idealer entweder im Denken oder Vorstellen wirklich oder aber als realer in einem der aufgeführten Verhältnisse zur Wahrnehmung stehe, so ergibt sich daraus eine Beziehung zwischen dem Subjekt der Aussage und dem Urteilenden selbst, die deutlich das Verhältnis der Wechselseitigkeit aufweist. Das Urteil: „Gott existiert“ rückt den Begriff „Gott“ zu dem Urteilenden[S. 55] selbst in eine Relation, die sich in den einander entsprechenden Formulierungen: „Ich muß Gott als existierend denken“ und: „Gott muß von mir als existierend gedacht werden“ darstellt.
Auf das erkenntnistheoretische Problem, das in dem Begriff der Existenz enthalten ist (das sog. „Realitätsproblem“, das in der Frage gipfelt, ob wir ein Recht haben, zu den in der Wahrnehmung gegebenen Objekten irgendwelche Korrelate als Ursachen dieser unabhängig von allem Bewußtsein anzunehmen, und wenn ja, von welcher Art diese — die sog. „Dinge an sich“ — gedacht werden müssen), soll hier nicht eingegangen werden; ebensowenig auf das psychologische, erkenntnistheoretische und logische Problem, das in dem Urteile „ich, der ich denke, existiere“ (Descartes’ „cogito ergo sum“) wurzelt, ein Problem, in dem sich Psychologie, Erkenntnistheorie und Logik am innigsten berühren (Problem des Selbstbewußtseins). Nur auf ein anderes soll noch kurz hingewiesen werden: Existentialurteile bedürfen wie alle Urteile über Tatsachen zum Erweise ihrer Gültigkeit einer zureichenden Begründung. Existentialurteile können also niemals Aussagen von unmittelbarer Gewißheit sein; lediglich das oben erwähnte Urteil „ich bin“ bildet als „cognitio intuitiva“ eine eigentümliche Ausnahme. Ideale Gegenstände sind als existierend zureichend begründet, wenn sie — wie die Begriffe der Mathematik — als formal denkmöglich oder wie die Vorstellungen der Phantasie als wirklich in unserem Bewußtsein angetroffen werden. Die Existenz realer Gegenstände dagegen kann nur durch Hinweis auf die Daten der Erfahrung begründet werden. In dem bloßen Begriff eines realen oder besser: real gedachten Gegenstandes ist niemals enthalten, ob diesem Existenz zukomme oder nicht. Es war ein Fehler Anselm von Canterburys und Descartes’, zu glauben, daß aus dem Begriff Gottes als des allervollkommensten Wesens die Tatsache seiner Existenz logisch notwendig gefolgert werden könne, da die Nichtexistenz seiner Vollkommenheit widerspräche (ontologischer Gottesbeweis). Die zureichende Begründung eines realen Existentialurteiles kann nie anders als durch Hinweis — sei es auf eigene, sei es auf fremde Wahrnehmung — gegeben werden, und wo in einer solchen Ableitungen aus anderen Urteilen eine Rolle spielen, gehen diese zuletzt doch auf Urteile zurück, deren Begründung in dem Hinweis auf die Wahrnehmung besteht. Das letztere ist z. B. der Fall, wenn wir aus gewissen gut erhaltenen Skeletten als überkommenen[S. 56] Resten einer prähistorischen Zeit schließen, daß es in jener eine andere Tierwelt gegeben habe wie heute.
Die entwickelte Theorie der Existentialurteile, die das Prädikat des Seins unmittelbar oder mittelbar in eine enge Beziehung zum Denken bzw. wahrnehmenden Erkennen rückt, geht im Prinzip auf die idealistische Formel der Berkeleyschen Lehre zurück, nach der alles Sein im Wahrgenommenwerden besteht („esse est percipi“), sowie auf die bereits mehr logisch fundierte Lehre David Humes, nach der alles Perzipieren Perzeption eines Seienden, der Begriff des Seins also der eines seiend Perzipierten ist. Wir nennen sie daher vielleicht am zweckmäßigsten „Perzeptionstheorie“ der Existentialurteile. In der neueren Logik findet sie sich in verwandter Form bei J. Geyser (Grdlgen. d. Log., 1909, S. 57 ff.) — Von dieser zu scheiden ist die sog. „Kausaltheorie“ des Existentialurteils, die im Prädikat der Existenz das Prädikat des Wirkens findet, die Aussagen über Sein oder Nichtsein also als kausale Relationsurteile deutet. Diese Auffassung geht ihrem Prinzip nach auf Leibniz zurück; sie findet sich in der neuen Logik vornehmlich vertreten durch B. Erdmann (Logik I2, S. 453 ff.).
Urteile, deren Subjekt selbst ein Urteil bildet, nennen wir Beurteilungen. Diese sind mithin Urteile über ein Urteil. Sie scheiden sich in drei Hauptgruppen: erstens in solche, die die Gültigkeit eines Urteils verneinen (verneinende Beurteilungen oder Negationen); zweitens in solche, die besagen, in welchem Umfange eine Urteilsbeziehung für ihr eigenes Subjekt gilt (quantitativ-bestimmende Beurteilungen); und drittens in solche, die über den Grad der Gültigkeit eines Urteils eine Entscheidung treffen (modal-bestimmende Beurteilungen).
Besprechen wir zunächst die erste Gruppe. Die logische Tradition seit Aristoteles faßt die bejahenden (positiven) und verneinenden (negativen) Aussagen als einander nebengeordnete Arten der Gattung Urteil auf (Koordinationstheorie). Seit dem Mittelalter (Apuleius) bezeichnet man den bejahenden und verneinenden Charakter des Urteils als dessen Qualität. Auch die meisten Logiker der neueren Zeit (so Wolff, Kant, Herbart, Lotze, Cohen, Windelband) halten an dieser Einteilung fest. Demgegenüber haben Chr. Sigwart und B. Erdmann (bei dem Cartesianer Arn. Geulincx angelegte Gedanken aufnehmend) darauf hingewiesen, daß das negative Urteil nicht eine dem positiven nebengeordnete Art des Urteils bilde, sondern daß vielmehr das positive Urteil das ursprüngliche von beiden sei und als solches dem negativen als Voraussetzung vorangehe[S. 57] (so auch Fr. Ed. Beneke; Wundt; Geyser). Nehmen wir als Beispiel der negativen Urteile die Aussage: „Bewußtseinsinhalte sind als solche nicht irgendwelche Erregungen der Nerven“, so wird darin nicht etwa dem Subjekt „Bewußtseinsinhalte als solche“ ein negatives Prädikat eingeordnet, sondern es wird die vorausgesetzte, vielleicht nur zum Zweck der Prüfung aufgestellte, in jedem Falle bestehende Behauptung, Bewußtseinsinhalte seien Erregungen der Nerven, als ungültig erklärt. Gegenstand der Verneinung ist also nicht das Subjekt des positiven Urteils („Bewußtseinsinhalte als solche“), nicht dessen Prädikat („sind irgendwelche Erregungen der Nerven“), sondern die in dem Urteil vollzogene Beziehung zwischen eben diesem Prädikat und dem Subjekt. Gegenstand der Verneinung ist mithin das positive Urteil, dem als Subjekt der Negation das Merkmal der Nichtgültigkeit als Prädikat eingeordnet wird ([S ← P] ← nicht-gültig). Die verneinende Beurteilung setzt demnach das positive Urteil voraus; sie nimmt Stellung zu einem bereits vollzogenen Urteil, dergestalt, daß sie dieses als nichtgültig erklärt (Primorditätstheorie des positiven Urteils).
Gegenüber dieser Deutung der verneinenden Urteile ist es belanglos, in welcher Form sprachlich die Verneinung zum Ausdruck gebracht wird. Ob ein Urteil eine verneinende Aussage bildet oder nicht, darüber entscheidet nicht der grammatische Bestand des Satzes, sondern der logische seines Inhalts. Grammatisch und ihrer Form nach können Urteile sehr wohl positiv sein, die ihrem Inhalt nach negativ sind. Denn die Verneinung braucht keineswegs immer durch die Partikel „nicht“ zum Ausdruck gebracht zu werden; sie kann vielmehr bereits in dem verbalen Bestande des Subjekts oder Prädikats selbst mitenthalten sein. Beispiele verneinender Beurteilungen sind demnach: „Kein Sterblicher hat noch des Lebens letzten Grund erfahren; und Roß und Reiter sah man niemals wieder; die Verurteilung des Sokrates war ungerecht; die meisten Menschen sind undankbar; Spinozas Dasein war glück- und freudelos.“ Verneinungen sind also nicht nur die Urteile von der Form „S ← nicht-P“, sondern auch die von der Form „S ← non-P“ (von Kant als limitative, d. h. einschränkende Urteile bezeichnet; von B. Erdmann neuerdings sehr treffend mittelbare Verneinungen genannt).
Ist die Negation ein Urteil über ein Urteil, so kann als Subjekt der Verneinung selbst wiederum eine Verneinung in Betracht kommen. Beispiele dafür sind: „Keine Rose ohne Dornen; kein schändlich’ Tun[S. 58] bleibt ungesühnt; keine Schrift des Aristoteles ist ohne Fehler überliefert worden; keine Möglichkeit einer Rettung wurde unversucht gelassen.“ Es ist ersichtlich, daß diese Urteile, Verneinungen einer Verneinung, ihrer Form nach negativ, ihrem Inhalte nach aber positiv sind. Sie sind nicht Bejahungen schlechthin, sondern verstärkte Bejahungen; und insofern sie sich dazu einer doppelten Negation bedienen, nicht unmittelbare Bejahungen wie die positiven Urteile im allgemeinen, sondern mittelbar bejahende Urteile. Als solche bilden sie ein Gegenstück zu den (eben erwähnten) mittelbar-verneinenden Urteilen, den Verneinungen von der Form S ← non-P. Diese Verhältnisse können wir als logischen Grundsatz der doppelten Verneinung formulieren: „Die Verneinung einer Verneinung ist eine mittelbare Bejahung“ (nach der scholastischen Formel: „duplex negatio: affirmatio“).
Kommen wir zur Besprechung der zweiten Gruppe: Quantitativ-bestimmende Beurteilungen sind solche, in denen darüber ausgesagt wird, in welchem Umfange das Prädikat eines vollzogenen Urteils von seinem Subjekt gilt. Sie zerfallen in die Arten der universalen (allgemeinen) und partikulären (besonderen) Urteile; das erstere besagt, daß die prädikative Beziehung zwischen S und P von dem ganzen Umfang des Begriffes S; das letztere, daß diese nur von einem Teil des Umfanges von S Gültigkeit habe ([S ← P] ← für alleeinige S gültig). Quantitativ-bestimmend ist dabei nur die Beurteilung; ihr Subjekt ist demgegenüber quantitativ-bestimmt; ihr Prädikat die quantitative Bestimmung selbst.
Universale Urteile sind entweder ursprünglich- oder empirisch-allgemein. Ursprünglich-allgemein sind Urteile, in denen die quantitative Bestimmung des Universalen lediglich auf Grund der in dem Subjekt des beurteilten Urteils enthaltenen Merkmale erfolgt (z. B. „alle Dreiecke mit gleicher Grundseite und Höhe sind flächengleich; alle Körper sind dreidimensional“). Empirisch-allgemein sind Urteile, deren Ursprung auf die Erfahrung gegründet ist. Die empirische Allgemeinheit ist entweder eine registrierende oder erweiternde. Registrierend-allgemein heißt ein Erfahrungsurteil, in dem lediglich das für eine Reihe von Arten der gleichen Gattung als gültig Erkannte in einem Urteil zusammengefaßt ist (alle bekannten S ← P); erweiternd-allgemein dasjenige,[S. 59] in dem — darüber hinausgehend — nicht nur den bekannten, sondern auch den noch unbekannten Arten einer Gattung insgesamt ein den bekannten Arten zukommendes Prädikat beigelegt wird (alle S schlechthin ← P). Beispiele für diese beiden Arten sind: 1. „Alle Bäume, die ich pflanzte, tragen reife Frucht“; — 2. „Alle Planeten drehen sich in Ellipsen um die Sonne“. — Dem allgemeinen Urteil „alle S ← P“ ist das Urteil „einige S ← nicht-P“ kontradiktorisch-entgegengesetzt; von beiden kann mithin nach dem Satze des Widerspruches nur eines gültig sein. Um das Urteil „alle S ← P“ zu widerlegen, genügt es also, daß man das Urteil „ein S ← nicht-P“ durch zureichende Begründung als gültig erweise. Demnach können wir den logischen Grundsatz aufstellen: das allgemein-bejahende Urteil (alle S ← P) wird durch das partikulär-verneinende (einige S ← nicht-P); das allgemein-verneinende Urteil (kein S ← P) durch das partikulär-bejahende (einige S ← P) mit zureichender Begründung widerlegt.
Partikuläre Urteile haben zumeist die Aufgabe, das entsprechende allgemeine entweder vorzubereiten („schon einige S ← P“) oder zu widerlegen (nur einige, also nicht alle S ← P). Ihnen kommt also gemeinhin entweder eine zum Allgemeinen aufsteigende oder das Allgemeine aufs Besondere einschränkende logische Funktion zu. Beispiele der ersteren Art sind: „einige Bienen haben bereits ihr Nest verlassen; einige Bestrebungen der sozialistischen Politiker sind bereits geglückt“; Beispiele der letzteren: „einige Gedanken Nietzsches haben in unreifen Köpfen unheilvolle Verwirrung angerichtet; einige der erlesensten Geister des Menschengeschlechtes sind von ihren Mitmenschen hingerichtet worden“. — Eine andere logische Funktion des partikulären Urteils ist die Kontrastierung. Diese kommt zum Ausdruck in der Ergänzung, auf die viele besondere Urteile ungesagt hinweisen; z. B. „einige neuere Ethiker sind Utilitaristen“ [ergänze: andere Idealisten oder Materialisten]; „wenige Menschen sind Linkshänder“ [ergänze: die meisten Rechtshänder].
Das partikuläre Urteil wird zum Grenzfall des singulären, wo die prädikative Beziehung eines Urteils als nur für eine einzige Art seines Subjektsbegriffes gültig beurteilt wird (z. B. „ein einziges Wort zur rechten Zeit hätte viel Unheil verhütet“). Die singulären Urteile ([S ← P] ← nur (oder: schon) für ein einziges S gültig) sind als quantitativ-bestimmende Beurteilungen von den individuellen oder Einzelurteilen als einfachen Aussagen streng zu scheiden. Ihre wesentlichen Unterschiede ergeben sich nach dem Gesagten von selbst.
[S. 60]
Wenden wir uns zur Besprechung der modal-bestimmenden Beurteilungen. Diese sind Urteile, in denen über den Grad der Gültigkeit eines Urteils ausgesagt wird. Dadurch sind sie von den Negationen charakteristisch verschieden. Das verneinende Urteil hebt die Gültigkeit des sein Subjekt bildenden Urteils auf; das modal-bestimmende dagegen gibt an, in welchem Grade das sein Subjekt bildende Urteil Geltung habe: und zwar, ob es entweder notwendig (apodiktisch) oder tatsächlich (assertorisch) oder auch nur möglicherweise (problematisch) gültig sei.
Apodiktische Beurteilungen sind also solche, deren Prädikat besagt, daß die in ihrem Subjekt gedachte Urteilsbeziehung denknotwendig gültig sei ([S ← P] ← notwendig gültig). Subjekte solcher Beurteilungen können alle unmittelbar-gewissen Urteile werden (z. B. die Axiome der Logik und reinen Mathematik), ebenso die mittelbar-gewissen (d. h. durch Ableitung aus unmittelbar-gewissen zureichend begründeten) Behauptungen. Diesen Urteilen ist ihrem Wesen nach das Merkmal apodiktischer Gültigkeit immanent. Aber auch nur diesen. Alle anderen Urteile (also diejenigen, die nicht dem Bereich der Gewißheit, sondern dem der Erfahrung angehören) können nicht Subjekte apodiktischer Beurteilung werden, weil das Merkmal der Denknotwendigkeit ihnen fehlt. Ein Zeichen für die Apodiktizität eines Urteils ist die Denkwidrigkeit (Denkunmöglichkeit) seines kontradiktorischen Gegenteils. 2 × 2 ist notwendig 4; denn der Gedanke, daß 2 × 2 nicht 4 sei, ist denkunmöglich. Verneinungen von apodiktischen Beurteilungen schließen nur die denknotwendige, nicht aber die tatsächliche und mögliche Gültigkeit des Urteils aus. Urteile ich: „es ist nicht denknotwendig, daß S ← P“, dann lasse ich jedenfalls die Möglichkeit zu, daß S ← P tatsächliche, bzw. mögliche Gültigkeit habe. (Für die Verneinungen modal-bestimmender Beurteilungen gilt im übrigen, was oben über Verneinungen im allgemeinen gesagt worden ist.)
Assertorische Beurteilungen sind solche, deren Prädikat besagt, daß die in ihrem Subjekt gedachte Beziehung tatsächlich gültig sei ([S ← P] ← tatsächlich gültig). Beispiele dieser sind: „es ist Tatsache, daß Napoleon nicht 1769, sondern 1768 geboren ist; tatsächlich gehören die Walfische nicht zu den Fischen, sondern zu den Säugetieren; es ist Tatsache, daß Christus gelebt hat“. Subjekte solcher Beurteilungen können alle Aussagen über Tatsachen (Realurteile, Wirklichkeitsbehauptungen)[S. 61] werden, deren Gültigkeit durch die Daten eigener oder überlieferter Erfahrung zureichend begründet ist. Ihr kontradiktorisches Gegenteil ist zwar denkmöglich, aber durch ebendieselben Daten der Erfahrung widerlegt. Die Behauptung, die Aussage S ← P sei tatsächlich gültig, schließt die Behauptung, daß sie überhaupt nicht gültig sei, aus, dagegen die Behauptung ihrer möglichen Gültigkeit ein; denn die tatsächliche Gültigkeit hat die mögliche zu ihrer Voraussetzung. Verneinungen assertorischer Beurteilungen verneinen zugleich die Möglichkeit apodiktischer Gültigkeit; denn was nicht als wirklich oder tatsächlich, das ist erst recht nicht als notwendig anzuerkennen. Sie lassen dagegen die Möglichkeit problematischer Geltung zu; denn, wo ich nur aussage, daß etwas sich in Wirklichkeit nicht zugetragen hat, schließe ich noch keineswegs aus, daß es sich hätte zugetragen haben können.
Problematische Beurteilungen endlich sind solche, deren Prädikat besagt, daß die in ihrem Subjekt gedachte Beziehung möglicherweise gültig sei ([S ← P] ← möglicherweise gültig). Beispiele dieser sind: „Licht ist möglicherweise eine Art der Elektrizität; Arminius der Cherusker und Sigfried, der Held der Nibelungen, sind möglicherweise eine und dieselbe Person; Homer kann gelebt haben; Ach, vielleicht, indem wir hoffen, hat uns Unheil schon betroffen; Epikur ist möglicherweise stark von Demokrit beeinflußt“[10]. Ohne auf das logisch mannigfach verwickelte Problem des Möglichen einzugehen, seien die Richtlinien zur Analyse der problematischen Beurteilungen kurz entwickelt. Subjekte solcher können alle Aussagen über Tatsachen werden, deren kontradiktorisches Gegenteil durch die Daten der Erfahrung nicht völlig widerlegt ist. Das Urteil: „Homer kann gelebt haben“ läßt die Möglichkeit offen, daß es einen Menschen dieses Namens nie gegeben hat. Die Urteile „Homer kann gelebt haben“ und „Homer hat vielleicht nicht gelebt“ schließen einander nicht aus, sondern bedingen geradezu einander. Die problematische Beurteilung steht also immer in einem korrelativem Verhältnis zu einem ihm entsprechenden Urteil, das logisch seine Ergänzung bildet. Das Urteil: „es ist[S. 62] möglich, daß es allwissende Wesen gibt“ ist logisch nur so lange gültig, wie auch das Urteil: „es ist möglich, daß es keine allwissenden Wesen gibt“ Gültigkeit hat. Beweisen, daß eine von beiden Beurteilungen falsch ist, heißt zugleich immer beweisen, daß die andere tatsächlich (nicht nur möglicherweise) gilt. Verneinungen problematischer Beurteilungen ([S ← P] ← unmöglich gültig = 〈[S ← P] ← möglicherweise gültig〉 ← nichtgültig) schließen auch die tatsächliche und notwendige Gültigkeit ihres Subjekts aus. Denn ein Urteil, dessen Gültigkeit denkunmöglich ist, kann auch nicht tatsächlich und ebensowenig notwendig gültig sein.
In der Mitte zwischen dem Möglichen und Tatsächlichen, aber eine Art des Möglichen bildend, steht das Wahrscheinliche. Wahrscheinlichkeit ist ein höherer Grad des Möglichen, ein niederer des Tatsächlichen. Urteile wie: „es ist wahrscheinlich, daß S ← P“ lassen das dazu korrelative: „es ist möglich, daß [S ← P] ← nichtgültig“ zwar zu; dieses erscheint ihnen gegenüber aber in der Form: „es ist nicht wahrscheinlich, daß [S ← P] ← nichtgültig.“ Aus diesen Unterscheidungen ergeben sich für die Logik Gradabstufungen des Möglichen von der durch geringfügigste Hoffnung getragenen bloßen Annahme bis zu den von stärkster Überzeugtheit durchdrungenen, fast an das Bewußtsein tatsächlicher Gültigkeit heranreichenden Wahrscheinlichkeitsbehauptungen. Dieses große Gebiet von modal-bestimmten Urteilen zwischen Möglichkeit und Tatsächlichkeit wollen wir als das der approximativen Beurteilungen (Wahrscheinlichkeitsbeurteilungen) bezeichnen.
Zusammengesetzte Urteile sind solche, die aus einer Mehrheit einfacher, einander koordinierter Urteile gebildet sind. Bereits die Beurteilungen sind als zusammengesetzte Urteile anzusprechen. Denn da in diesen das Subjekt selbst ein Urteil ist, gehen sie über den materialen Bestand des einfachen Urteils (S ← P) hinaus. Sie stehen aber kraft der besonderen Beziehung, in die in ihnen das beurteilte Urteil und die Beurteilung selbst zueinander treten, den einfachen Urteilen näher als die jetzt zu besprechenden Arten der zusammengesetzten Urteile, bilden mithin die Grenze dieser zu den einfachen.
[S. 63]
Sehen wir von den Beurteilungen ab, so ist es zweckmäßig, die zusammengesetzten Urteile in zwei Hauptarten zu scheiden. Sie sind Urteilsverbindungen, wo das die einfachen Urteile miteinander verknüpfende Band in einem gemeinsamen materialen Urteilsbestandteil (Subjekt oder Prädikat) zu suchen ist; diese zerfallen in kopulative, konjunktive und divisive Verbindungen. Sie sind Urteilsgefüge, wo das die einfachen Urteile miteinander verknüpfende Band in der formal-logischen Beziehung, die zwischen diesen Urteilen besteht, zu suchen ist; sie zerfallen in disjunktive und hypothetische Gefüge.
Besprechen wir zuerst die Urteilsverbindungen. Kopulative Urteilsverbindungen sind solche, in denen eine Mehrheit von Urteilen mit gleichem Prädikat, aber verschiedenen Subjekten zu einem Urteil verknüpft ist ([S1 und S2 und S3 ... Sn] ← P). Beispiele dafür sind: „Lust und Liebe sind die Fittiche zu großen Taten; vom Eise befreit sind Strom und Bäche; Berlin, Bonn, Königsberg, Halle, Jena ... sind Universitätsstädte“ (Verneinungen: „Weder Reichtum noch Macht stellen verlorene Ehre wieder her“). Die Zahl der einfachen Urteile, die in eine kopulative Urteilsverbindung eingehen können, darf nicht geringer sein als zwei, kann nach oben aber ins Unendliche gehen; denn, wenn nicht praktische und ästhetische Gründe es verböten: logischerseits wäre es angängig, eine beliebig große Anzahl von Urteilen mit gleichem Prädikat, aber verschiedenen Subjekten zu einem Urteil zu verbinden. — Konjunktive Urteilsverbindungen sind solche, in denen eine Mehrheit von Urteilen mit gleichem Subjekt, aber verschiedenen Prädikaten zu einem Urteil verknüpft ist (S ← [P1 und P2 und P3 ... Pn]). Beispiele dieser sind: „Alles rennet, rettet, flüchtet; etwas fürchten, hoffen und sorgen muß der Mensch für den kommenden Morgen; er lebte, nahm ein Weib und starb; edel sei der Mensch, hilfreich und gut“ (Verneinungen: „Bin weder Fräulein weder schön; Kants kritische Hauptwerke sind weder leicht zu verstehen noch leicht darzustellen“). Für die Zahl der einfachen Urteile, welche die konjunktiven Verbindungen bilden, gilt das gleiche wie das oben für die kopulativen Verbindungen Gesagte. — Divisive Urteilsverbindungen sind solche, in denen eine Mehrheit koordinierter partikulärer Urteile mit verschiedenem Subjekt, aber gleichem Prädikat zu einem Urteil verknüpft ist (S ← [teils P1, teils P2, teils P3 ... Pn]). Die logische Analyse ergibt als Elemente der divisiven Urteilsverbindung[S. 64] die partikulär-bestimmenden Beurteilungen: [S ← P1] ← gilt für einige S; [S ← P2] ← gilt für einige S; [S ← P3] ← gilt für einige S usw., die miteinander verknüpft ergeben: S ← teils P1, teils P2, teils P3 ... usw. Beispiele dafür sind: „Körper sind ihrem Aggregatzustande nach teils feste, teils flüssige, teils gasförmige; die Inhalte des Bewußtseins sind teils gegenständliche (Vorstellungen oder Begriffe), teils zuständliche (Lust oder Unlust); Bakterien sind teils Kokken, teils Bazillen, teils Spirillen.“ Das Prädikat diviser Verbindungen enthält also die Arten, welche ihrem Subjekt als deren Gattungsbegriff zukommen, entwickelt mithin eine vollständige Einteilung des Umfangs ihres Subjekts. Als spezielle Bedingungen der formalen Gültigkeit der divisiven Verbindung seien hier genannt: 1. Divisive Urteilsverbindungen müssen erschöpfend sein (d. h.: die ausgesagten Arten müssen den ganzen Umfang des Subjektsbegriffes umfassen); 2. die ausgesagten Arten müssen nach einem und demselben Gesichtspunkte der Einteilung gewählt und einander koordiniert sein.
Kommen wir zu den Gefügen. Disjunktive Urteilsgefüge sind solche, die aus einer Mehrheit koordinierter, sich in ihrer Gültigkeit einander ausschließender problematischer Beurteilungen mit gleichem Subjekt oder Prädikat gebildet sind ([entweder S1 oder S2 oder S3 ... Sn] ← P; S ← [entweder P1 oder P2 oder P3 ... Pn]). Beispiele dafür sind: „Der Raum ist entweder ein reales Wesen oder eine Form sinnlicher Anschauung; entweder Newton oder Leibniz hat die Unendlichkeitsrechnung zuerst begründet.“ Die disjunktiven Gefüge sind den Urteilsverbindungen verwandt, insofern als die Elemente, aus denen sie bestehen, gleichfalls einander koordiniert sind. Sie unterscheiden sich aber von diesen charakteristisch dadurch, daß in ihnen die Glieder der Zusammensetzung zueinander in einem bestimmten logischen Verhältnis stehen, das beiden Urteilsverbindungen fehlt. Urteilt man: S ← [P1 und P2 und P3] oder [S1 und S2 und S3] ← P, so gilt jedes der einfachen Urteile, aus denen diese Verbindungen zusammengesetzt sind, unabhängig vom anderen. Zerlegt man die divisive Verbindung S ← [teils P1, teils P2, teils P3] in ihre Bestandteile (einige S ← P1, einige S ← P2 usw.), so kommt jedem dieser Urteile eine Gültigkeit zu, die von der Gültigkeit des anderen unabhängig ist. Nicht so bei den disjunktiven Gefügen. Das Urteil: S ← [entweder P1 oder P2] besagt: S kann entweder P1 oder P2 sein; und mehr noch: wenn S ← P1 [S. 65]gültig, dann S ← P2 nichtgültig; und wenn S ← P2 nichtgültig, dann S ← P1 gültig und umgekehrt. Daraus ergibt sich fürs erste, daß die elementaren Glieder des disjunktiven Gefüges problematische Beurteilungen sind, und zum zweiten, daß diese sich einander in ihrer Gültigkeit ausschließen, dergestalt, daß, wenn eines von ihnen gültig ist, die anderen ungültig sein müssen; wenn alle bis auf eines ungültig sind, dieses letzte gültig sein muß.
Disjunktive Gefüge sind geradeso wie die divisiven Verbindungen formal nur gültig, wenn sie erschöpfend sind, d. h.: wenn die in ihnen enthaltenen einander ausschließenden Prädizierungen das ganze Gebiet der vorhandenen Möglichkeiten umfassen. Kontradiktorische Disjunktionen nennen wir alle diejenigen disjunktiven Gefüge, deren Elemente kontradiktorisch-entgegengesetzte Urteile sind (S ← [entweder P oder nicht-P]). Beispiele dafür sind: „Der Wille des Menschen ist entweder frei oder nicht frei; der Angeklagte ist entweder schuldig oder nicht schuldig.“ Konträre Disjunktionen heißen dementsprechend alle diejenigen, die aus konträr-entgegengesetzten Urteilen zusammengesetzt sind, d. h. solchen, die bei gleichem Subjekt konträr-entgegengesetzte Prädikate haben. Als Beispiele dieser seien angeführt: „Die Welt ist entweder geschaffen oder von Ewigkeit her vorhanden; Schauspiele sind entweder Lust- oder Trauerspiele.“ Spezifische Disjunktionen nennen wir endlich (mit B. Erdmann) alle diejenigen disjunktiven Gefüge, deren Elemente weder kontradiktorisch- noch konträr-entgegengesetzte Urteile sind. Als Beispiele dieser seien genannt: „Jene spartanische Mutter wollte, daß ihr Sohn entweder mit dem Schilde oder auf dem Schilde aus der Schlacht heimkehre; die Verfassung eines Staatswesens ist nach Aristoteles entweder monarchisch oder oligarchisch oder demokratisch; ich wünschte, die Nacht oder die Preußen kämen.“ Ohne besondere logische Bedeutung sind Disjunktionen wie: „Der Mensch ist entweder von Natur gut oder schlecht oder beides nicht“ (Mischform der konträren und kontradiktorischen Disjunktion), sowie: „Gefühle sind entweder Zustände der Lust oder Unlust oder eigentümliche Mischungen beider“ (Mischform der konträren und spezifischen Disjunktion). Disjunktive Gefüge sind schließlich auch in komplizierteren Formen möglich, dergestalt, daß die Elemente ihrer Zusammensetzung weder Subjekt noch Prädikat miteinander gemeinsam haben, so also, daß die materialen Urteilsglieder in diesen völlig wechseln (entweder S ← P oder Q ← R). An der Hand eines Beispiels: „Entweder du trittst für ihn ein, oder es gibt keine Dankbarkeit mehr; Entweder wir siegen, oder das Leben ist nicht mehr lebenswert.“ Diese Gefüge sind als verwickelte von den oben besprochenen als reinlichen zu scheiden. Ihre logische Analyse führt auf folgende Urteile als einfache Bestandteile: 1. S ← [entweder P oder nicht-P], 2. wenn [S ← P] ← nichtgültig, dann Q ← R. Zusammengezogen: entweder S ← P oder Q ← R. Sie setzen mithin die hypothetischen Gefüge voraus, die erst jetzt zur Besprechung kommen. Betont sei noch, daß disjunktive Gefüge als Urteile auch Subjekte von Beurteilungen sein können. In sich zusammengesetzt aus problematischen Beurteilungen, vermögen sie selbst wiederum Gegenstände problematischer, assertorischer[S. 66] oder apodiktischer Beurteilung zu werden (es ist möglich, tatsächlich, notwendig, daß S ← [entweder P1 oder P2 oder P3]). An Beispielen: „Der Wille des Menschen kann entweder frei oder gebunden sein (problematisch); tatsächlich ist der Krieg entweder ein Segen oder ein Unheil für die Menschheit (assertorisch); ganze Zahlen sind notwendigerweise entweder gerade oder ungerade (apodiktisch).“
Hypothetische Urteilsgefüge sind solche, die aus zwei miteinander in dem Verhältnis von Grund und Folge verbundenen Urteilen bestehen (wenn Q ← R, dann S ← P; oder, indem wir Q ← R = G (Grund) und S ← P = F (Folge) setzen: wenn G, dann F). Beispiele dafür sind: „Wenn die Könige bauen, haben die Kärrner zu tun; wenn du den Halys überschreitest, wirst du ein großes Reich zerstören; wenn der Mantel fällt, muß der Herzog nach; Raffael wäre ein großer Maler geworden, selbst wenn er ohne Hände auf die Welt gekommen wäre.“ Hypothetische Gefüge sind ihrem Sinn nach auch Urteile wie: „Wer gut schmiert, fährt gut; ein jeder kehre vor seiner Tür, und rein ist jedes Stadtquartier; willst du dich selber erkennen, so sieh, wie die andern es treiben; man fühlt die Absicht, und man wird verstimmt; allzu straff gespannt zerspringt der Bogen.“ Die eigentümliche — als „hypothetisch“ bezeichnete — Beziehung, in die in den hypothetischen Gefügen der in der traditionellen Logik sog. „Vordersatz“ (wenn Q ← R = Hypothesis) zu dem sog. „Nachsatz“ (dann S ← P = Thesis) gerückt wird, bedarf besonderer Erörterung. Die geläufige Auffassung der hypothetischen Gefüge geht dahin, daß der Nachsatz als durch die Gültigkeit des Vordersatzes bedingt ausgesagt werde (sog. „Nachsatztheorie“). Diese Deutung der hypothetischen Gefüge (vertreten z. B. durch Chr. Wolff) scheitert aber an denjenigen Aussagen, in denen ersichtlich jedes der beiden Urteile für sich als nichtgültig bewußt ist, und doch das Ganze, d. h. der logische Zusammenhang beider Urteile mit dem Bewußtsein der Gültigkeit gedacht wird (z. B.: „Bestände das Glück in körperlichen Lustgefühlen, so müßte man die Ochsen glücklich nennen, wenn sie Erbsen fressen“ [Heraklit]). Ausgesagt ist also in den hypothetischen Gefügen nicht ein Urteil, das in seiner Gültigkeit durch die eines anderen bedingt ist, sondern ein Urteilszusammenhang, in dem die beiden Elemente als im Verhältnis von Grund und Folge, mithin im Verhältnis logischer Konsequenz zueinander stehend gedacht sind („Konsequenztheorie des hypothetischen Gefüges“ nach der Namengebung B. Erdmanns). — „Sagen wir: ‚Wenn der Koran von[S. 67] Gott herrührt, so ist Muhammed der Prophet Gottes‘ (heißt es bei John Stuart Mill), so wollen wir damit weder behaupten, daß der Koran von Gott herrührt noch auch, daß Muhammed in Wahrheit sein Prophet ist. Keiner von diesen beiden einfachen Sätzen mag wahr sein, und doch kann die Wahrheit des hypothetischen Satzes unbestreitbar sein. Was ausgesagt wird, ist nicht die Wahrheit irgendeines von den beiden Sätzen, sondern die Tatsache, daß der eine aus dem anderen gefolgert werden kann. Was ist also das Subjekt und was ist das Prädikat des hypothetischen Satzes? Der Koran ist nicht sein Subjekt, und ebensowenig ist es Muhammed. Denn es wird weder vom Koran noch von Muhammed etwas bejaht oder verneint. Das wahrhafte Subjekt der Prädizierung ist der ganze Satz: ‚Muhammed ist der Prophet Gottes‘, und die Aussage ist die, daß dies eine berechtigte Folgerung aus dem Satze ist: ‚der Koran rührt von Gott her‘.“ — Im hypothetischen Gefüge besteht also kurz gesagt das Subjekt in der Thesis (S ← P), das Prädikat in der Aussage, daß die Thesis von der Hypothesis (wenn Q ← R) so abhängt wie die logische Folge von ihrem Grunde.
Entsprechend der oben entwickelten Scheidung der Urteile in Formal- und Realbehauptungen zerfallen auch die hypothetischen Gefüge in formale und reale. Beispiele formaler hypothetischer Gefüge sind: „Wenn zwei Geraden ins Unendliche verlängert sich nirgends einander schneiden, so sind sie parallel; wenn zwei Kegel Grundfläche und Höhe miteinander gemeinsam haben, so haben sie gleichen Rauminhalt; wenn ein Dreieck spitzwinklig ist, so kann keiner seiner Winkel einen Rechten und mehr betragen; wenn von zwei kontradiktorisch-entgegengesetzten Urteilen eines als gültig erwiesen ist, dann ist das andere notwendig ungültig.“ Diese sind hypothetische Gefüge formal-logischer Konsequenz. Der Zusammenhang zwischen Grund und Folge in ihnen ist ein unmittelbar oder mittelbar gewisser, mithin denknotwendiger; ihr kontradiktorisches Gegenteil ist daher denkunmöglich. Sie können also auch Gegenstände apodiktischer Beurteilung werden (wenn G, so notwendig F); sie sind ferner umkehrbar, d. h. auch dann gültig, wenn man Grund und Folge miteinander vertauscht (darüber an späterer Stelle). — Beispiele hypothetischer Gefüge über Tatsachen sind bereits oben gegeben worden. Diese bedürfen wie alle Urteile über Tatsachen einer zureichenden Begründung, die sich letzten Endes auf die Elemente der Wahrnehmung stützt. Sie sind ihrer Konsequenzbeziehung nach nicht alle von der gleichen Art. Wir können vielmehr hypothetische Gefüge zeitlicher, kausaler und teleologischer Konsequenz scheiden. Hypothetische Gefüge zeitlicher Konsequenz sind: „Wenn die Schule beendet ist, bevölkern sich Straßen und Plätze mit Knaben und Mädchen; wenn die Schwalben nach südlicheren Ländern ziehen, naht der Herbst.“ Hypothetische Gefüge kausaler Konsequenz — mit den eben erwähnten durch mannigfache Übergangsformen verbunden und nicht reinlich von diesen zu scheiden — sind:[S. 68] „Wenn man einen Wurm tritt, krümmt er sich; wenn man Wasser bis auf 100° erwärmt, verdampft es; wenn man Sand, Soda und Marmor in bestimmten Mengen in einem Tiegel schmilzt, erhält man eine feste, farblose Masse, die man Glas nennt.“ Hypothetische Gefüge teleologischer Konsequenz — ihrem Wesen nach teils theoretischer (Normen des Denkens), teils praktischer Natur (Normen des Handelns) — sind: „Wenn Urteile wahr sein sollen, müssen sie sowohl den Bedingungen der formalen wie materialen Gültigkeit entsprechen; wenn es Gerechtigkeit im Staate geben soll, müssen Gesetze nicht nur da sein, sondern auch befolgt werden; willst du genau erfahren, was sich ziemt, so frage nur bei edlen Frauen an.“ Hypothetische Gefüge über Tatsachen können sowohl Gegenstände assertorischer wie auch problematischer Beurteilungen werden (wenn G, so tatsächlich F; wenn G, so möglicherweise F). Verneinungen hypothetischer Gefüge sind jene Formen, in denen die Konsequenzbeziehung zwischen G und F geleugnet ist (wenn G, so nicht F = [wenn G, so F] ← nichtgültig); z. B. „wenn der Herr mit uns ist, wird der Segen unserem Werke nicht fehlen.“ Die hypothetischen Gefüge der Form: ‚wenn G nicht, so F‘ und ‚wenn G nicht, so F nicht‘, sind mithin nicht Verneinungen hypothetischer Gefüge, sondern bejahenden Charakters, das letztere ein bejahendes hypothetisches Gefüge durch doppelte Verneinung. — Sofern in hypothetischen Behauptungen der angegebene Grund als der allein mögliche für die ausgesagte Konsequenz gedacht ist, heißen diese „hypothetische Gefüge ausschließlicher Konsequenz“ (nur wenn G, dann F).
Aus den hypothetischen Gefügen logisch ableitbar sind Urteilsformen wie: weil Q ← R, darum S ← P und: obschon Q ← R, dennoch S ← P. Setzen wir z. B. den in dem logischen Grund eines hypothetischen Gefüges (wenn Q ← R) enthaltenen Urteilsgedanken als gültig voraus, so entsteht die kausale Urteilsform: weil Q ← R, darum S ← P; setzen wir z. B. den in der Folge (S ← P) enthaltenen Urteilsgedanken als gültig, den im Grunde enthaltenen dagegen als nichtgültig, dann entsteht die konzessive Form: obschon [Q ← R] ← nichtgültig, S ← P. An diesen Formen überwiegt das grammatische Interesse das logische; darum sei ihrer Erörterung kein weiterer Raum gewährt.
Prüfen wir das Verhältnis von Urteil und Frage logisch, so ergibt sich — wie schon früher betont —, daß die Frage das Urteil voraussetzt. Aus dem mißglückten Versuch, ein Urteil zu vollziehen — oder auch, was damit der Sache nach übereinkommt, aus dem Zweifel an der Gültigkeit eines vollzogenen Urteils — ergibt sich eine Ungewißheit, die wir durch das Mittel der Fragestellung zu überwinden trachten. Der Ursprung der Frage liegt mithin logisch in einer Urteilshemmung;[S. 69] sie selbst ist der Ausdruck einer Ungewißheit, verbunden mit dem Wunsche, diese zu überwinden. Insofern kommt ihr selbst Urteilscharakter zu. Die Frage: „Ist S ← P?“ bedeutet logisch soviel wie: „Ich weiß nicht, ob S ← P gültig ist, und wünsche es zu wissen.“ Das aussagende Element liegt darin in dem Zugeständnis der Unwissenheit und dem Ausdruck des Wunsches. Demnach steht die Frage den Beurteilungen näher als den Urteilen im eigentlichen Sinne. Die den Inhalt der Frage bildende Aussage: „ich weiß nicht, ob S ← P gültig ist, und wünsche es zu wissen“ ist ein Urteil über ein Urteil, von dem ausgesagt wird, daß seine Gültigkeit ungewiß sei, und daß die Gewißheit über Gültigkeit oder Ungültigkeit gewünscht werde. Sind die Fragen mithin ihrem aussagenden Charakter nach nicht Urteile schlechthin, sondern Beurteilungen, so stimmt das treffend mit der aufgestellten Theorie überein, daß die Frage nicht dem Urteil vorangehe, sondern dieses voraussetze.
Der Urteilscharakter der Frage darf indessen den charakteristischen Unterschied zwischen Urteil und Frage nicht verschleiern. Ein Urteil ist immer die vollzogene Einordnung eines Prädikats- in den Inhalt eines Subjektsbegriffes, verbunden mit dem Bewußtsein, daß die ausgesagte Beziehung zwischen S und P gültig sei. Das gilt für alle Urteile, sowohl für die einfachen wie für die zusammengesetzten, seien sie Beurteilungen, Verbindungen oder Gefüge. Eine Frage dagegen ist immer der Ausdruck einer Ungewißheit, verbunden mit dem Wunsche, diese zu überwinden. Insofern ist die Frage trotz ihres Urteilscharakters von dem Urteil wesentlich verschieden und am ehesten noch als dessen Gegenteil zu bezeichnen. Will man beide, Urteil und Frage, unter einem höheren Gattungsbegriff zusammenfassen, dann kann man sagen, es gibt zweierlei Aussagen: behauptende Aussagen oder Urteile; fragende Aussagen oder Fragen.
Ob eine Aussage eine behauptende oder fragende ist, darüber entscheidet nicht deren sprachliche Formulierung, sondern deren logischer Sinn. Man nehme etwa Aussagen wie: „Kann ich Armeen aus der Erde stampfen, wächst mir ein Kornfeld in der flachen Hand?; was ist göttlicher als vergeben?; was ist das Leben ohne Liebesglanz?; und muß ich so dich wiederfinden?; wie kommt mir solcher Glanz in meine Hütte?“, so bedarf es keiner näheren Begründung, daß es sich hier um nur scheinbare Fragen, um in das Gewand der Frage gehüllte behauptende Aussagen handelt. Indem sie entweder die auf die Frage zu erteilende allein mögliche Antwort in dem Sinn der Frage und der Art ihrer Formulierung deutlich zum Ausdruck bringen oder aber als Ausdruck der Klage, des Schmerzes, der Verwunderung, der Verzweiflung[S. 70] überhaupt keinerlei Antwort bedürfen, sind sie Urteile besonders betonter Gewißheit, nicht Fragen. Der Ausruf: „Was sind Hoffnungen, was sind Entwürfe ...?“ z. B. ist ein Urteil über die Nichtigkeit des menschlichen Hoffens und Planens; der Ausruf: „Und muß ich so dich wiederfinden?“ ein Urteil, dessen Prädikat die Klage über das „So-wiederfinden“, dessen Subjekt der Urteilende selbst ist. Für die Formulierung solcher — meist subjektiver und subjektiv-gültiger — Ausbrüche der Leidenschaft in Form von Fragen sind übrigens weniger logische als psychologische und ästhetische Gründe maßgebend. (Scheinbare Fragen sind auch die sog. prüfenden Fragen, die etwa von einem Lehrer einem Schüler gestellt werden, um zu erfahren, ob der Schüler die darauf gültige Antwort weiß. Ihnen kommt nur psychologische und pädagogische, keine logische Bedeutung zu.)
Die Einteilung der Fragen richtet sich nach demjenigen Urteilselement, durch dessen Mangel der Versuch zu urteilen unausführbar wird. Fehlen kann in ihnen entweder eines der materialen Bestandteile des gewünschten Urteils (Subjekt, Prädikat) — (sie sollen danach materiale Fragen heißen) — oder auch das Bewußtsein, daß die in einem Urteil vollzogene Beziehung zwischen Subjekt und Prädikat gültig sei; wir nennen diese daher Gültigkeitsfragen.
Wenden wir uns zu den ersteren. Materiale Fragen sind solche, in denen entweder Auskunft gewünscht wird über das Subjekt, dem ein gegebenes Prädikat, oder über ein Prädikat, das einem gegebenen Subjekt eingeordnet werden soll. Sie sind danach teils Subjekts-, teils Prädikatsfragen. Die Form der ersteren ist: Wer (was) ← P?; die Form der zweiten: S ← was (wie beschaffen)? Dabei braucht bei den Subjekts- und Prädikatsfragen durchaus nicht das ganze Subjekt oder Prädikat unbekannt zu sein. Es kann z. B. die Gattung bekannt sein und nur die spezielle Art fehlen; ja, es kann sogar die spezielle Art gegeben sein, und der gewünschte Urteilsbestandteil nur in einer näheren Bestimmung des Subjekts oder Prädikats bestehen, beim Subjekt etwa in der Quantität (wie viele S ← P?), beim Prädikat in der Angabe von Ort, Zeit, Beschaffenheit usw. (wann, wo, wie beschaffen). Die Frage: wie viele S ← P? entspricht dabei den quantitativ-bestimmenden Beurteilungen; sie muß also genau genommen lauten: [S ← P] gilt für wie viele S? und gehört mithin nicht zu den Subjekts-, sondern zu den Prädikatsfragen.
Beispiele von Subjektsfragen sind: „wer lacht da?; wer tat mir das?; was ist geschehen?; welches Buch fehlt dir?; wer will ihn wiederholen?; wessen Haus brennt?; wer von ihnen war dabei?“; Beispiele von Prädikatsfragen: „was ist der langen Rede kurzer Sinn?; was sagte der Vater?; was willst du mit dem Dolche? sprich; von wannen kommt dir diese Wissenschaft?;[S. 71] wem gab er das Buch?; wann wird der Retter kommen diesem Lande?“ — Hypothetische Subjektsfragen sind: wenn Q ← R, was dann? (z. B.: „Wenn es nun nicht gelingt, was dann?“); hypothetische Prädikatsfragen: wann oder unter welcher Bedingung ist S ← P gültig? (z. B.: „Unter welcher Bedingung ist der Feind geneigt, Frieden zu schließen?“ Antwort: ... wenn wir ... usw.). Zu den materialen Fragen gehören auch kausale Fragen wie: warum ist S P? (weil Q ← R), ebenso finale Fragen: wozu ist S P? (damit Q ← R).
Gültigkeitsfragen sind im Unterschied zu den materialen alle diejenigen, in denen darüber Auskunft gewünscht wird, ob die in einem Urteil vorhandene prädikative Beziehung zwischen Subjekt und Prädikat gültig sei. Die einfachste Form dieser Fragen ist die elementare Gültigkeitsfrage von der Form: ist S ← P gültig? (Antwort: ja — nein). Diese geht in die Form der disjunktiven Gültigkeitsfrage über, wo wir die in einem disjunktiven Gefüge zugestandene Unwissenheit, welche von mehreren einander ausschließenden Urteilsmöglichkeiten gültig sei (S ← [entweder P1 oder P2]; entweder S1 oder S2 ← P), in Gestalt einer Frage formulieren (ist S ← P1 oder P2?; ist S1 oder S2 ← P?). Dem hypothetischen Urteilsgefüge, in dem die Beziehung von Grund und Folge ungewiß ist, entspricht die hypothetische Gültigkeitsfrage (ist S ← P, wenn Q ← R?). Mischformen hypothetischer und disjunktiver Gültigkeitsfragen endlich sind Fragen von der Form: wenn Q ← R, ist dann S ← P1 oder P2?
Beispiele elementarer Gültigkeitsfragen sind: „Ist es geschehen?; bist du’s, Hermann, mein Rabe?; hat die Vorstellung schon begonnen?“; Beispiele disjunktiver (1) und hypothetischer (2) Gültigkeitsfragen sowie deren Mischformen (3): 1. „Bist untreu, Wilhelm, oder tot?; wer wagt es, Rittersmann oder Knapp, zu tauchen in diesen Schlund?“ — 2. „Wird er kommen, wenn ich ihn bitte?; würde er gesiegt haben, wenn er die Schlacht begonnen hätte?“ — 3. „Wenn er nun vor Gericht kommt, wird er verurteilt oder freigesprochen werden?“ — Aus der Ungewißheit der Beziehungen kausaler, finaler und konzessiver Urteilszusammenhänge erwachsen ferner Fragen von der Form: ist S ← P, weil Q ← R?; ist S ← P, damit Q ← R; ist S ← P, obgleich Q ← R?; wir nennen diese entsprechend der bisherigen Namengebung: kausale, finale und konzessive Gültigkeitsfragen.
Liegt es im Wesen der Frage, daß sie als Ausdruck einer Ungewißheit zugleich das Begehren nach Gewißheit in sich befaßt, so kann naturgemäß das Verlangen des Fragenden erst befriedigt sein, wenn die erteilte Antwort dasjenige Element enthält, das dem Fragenden beim Vollzug des versuchten Urteils gefehlt hat. Die Bedingungen der Gültigkeit der Antwort auf eine Frage sind den formalen und[S. 72] materialen Bedingungen der Gültigkeit von Urteilen überhaupt gleich; denn die Antwort ergänzt den der Frage zugrunde liegenden mißglückten Urteilsversuch zu dem gewünschten Urteil; sie ist insofern, unabhängig von ihrem grammatischen Bestand, ja unabhängig von ihrer sprachlichen Ausdrucksform (sie kann eine Handbewegung ebenso sein wie ein Kopfnicken), ein Urteil.
Die logische Bedeutung der Frage liegt darin, daß sie als Ausdruck eines nach Gewißheit verlangenden Zustandes unbefriedigender Ungewißheit das Denken von unzulänglichen oder zweifelhaften Urteilen zu immer erneuten Urteilsversuchen hinleitet. Auch Fragen bedürfen wie Urteile einer zureichenden Begründung. Eine Frage ist zureichend begründet, wenn sie richtig gestellt ist; sie ist unzureichend begründet, wenn sie den Bedingungen einer richtigen Fragestellung nicht entspricht. Insbesondere für das wissenschaftliche Denken, in dem die Fragestellung zur Problemstellung wird, ist die Forderung einer zureichenden Begründung auch für die Frage außerordentlich wichtig; daher wird in der logischen Methodenlehre darauf noch zurückzukommen sein.
[6] Kants fernere Scheidung der Urteile in analytische und synthetische hat nicht logische, sondern transzendental-philosophische Bedeutung. Unter analytischen Urteilen versteht Kant solche, die im Prädikat nur enthalten, was im Begriff des Subjekts schon als notwendiges Merkmal gedacht ist (erläuternde Urteile; z. B.: „Alle Körper sind ausgedehnt“); unter synthetischen Urteilen solche, die im Prädikat enthalten, was im Begriff des Subjekts noch nicht notwendig gedacht ist (erweiternde Urteile; z. B. „Einige Körper sind schwer“). Zur Kritik dieser Scheidung vgl. B. Erdmann, Logik I2, Kap. 38.
[7] So z. B. von der „Anerkennungstheorie“ des Urteils bei Franz Brentano, die historisch genommen bis auf die Stoa, Augustin, Thomas von Aquino, Descartes, Malebranche und Hume (Lehre vom belief) zurückgeht, in der neuen Logik in verwandter Form auch von W. Hamilton und Al. Bain in England, von A. Marty, W. Windelband und H. Rickert in Deutschland vertreten wird. Vgl. dazu Näheres bei B. Erdmann, Logik I2, Kap. 46: Jos. Geyser, Grundlagen d. Logik, 1909, S. 157 ff., 163 ff.
[8] Bei der Lektüre mag dieses logische Symbol getrost durch die grammatische Kopula „ist“ (bzw. „sind“) ausgedrückt werden.
[9] Man vergleiche zu Problemstellung und Lösung: B. Erdmann, Über Inhalt und Geltung des Kausalgesetzes, Halle 1904.
[10] Man beachte: Nicht alle Urteile, deren Prädikat das Wort „können“ enthält, sind problematische. „Können“ bedeutet im Deutschen ebenso ein „fähig-sein“ wie ein „möglich-sein“. Problematische Urteile sind also nicht Urteile wie: „ich kann Französisch, ich kann laufen, ich kann dichten, ich kann singen, Kinder können erzogen werden“.
Schließen heißt im logischen Sinne des Wortes: aus einem oder mehreren gegebenen Urteilen ein davon verschiedenes denknotwendig ableiten. Ein Schluß ist demnach derjenige Denkprozeß, durch den aus einem oder mehreren gegebenen Urteilen ein davon verschiedenes denknotwendig abgeleitet wird. Die überlieferte Logik unterscheidet zweierlei Hauptarten von Schlüssen: unmittelbare oder Folgerungen und mittelbare oder Schlüsse im eigentlichen Sinne. Unmittelbare Schlüsse sind solche, in denen die Ableitung aus einem, mittelbare solche, in denen die Ableitung aus einer Mehrheit von Urteilen erfolgt.
Ist die Folgerung die denknotwendige Ableitung eines Urteils aus einem davon verschiedenen gegebenen Urteil, so ist sie als Ganzes aus zwei Urteilen zusammengesetzt: dem Folgerungsurteil als demjenigen, welches — dem Grundurteil als demjenigen, aus welchem gefolgert wird[11]. Es ist ersichtlich, daß für das Folgerungsurteil[S. 73] zwei spezielle Bedingungen seiner formalen und materialen Gültigkeit in Betracht kommen: 1. die formale und materiale Gültigkeit seines Grundurteils, 2. die formale Gültigkeit des Folgerungsprozesses selbst. Die Gültigkeit des Folgerungsurteils — unter der Voraussetzung einer formal gültigen Ableitung — steht und fällt also mit der Gültigkeit des Grundurteils.
Die speziellen Arten der Folgerungen ergeben sich aus der Verschiedenheit der formalen Veränderungen, durch die aus dem Grundurteil das Folgerungsurteil gewonnen wird. Die traditionelle Logik unterscheidet als Hauptarten der Folgerungen solche durch: formale Äquipollenz; Konversion; Kontraposition; Subalternation und Opposition; zu diesen kommen noch zwei weniger wichtige Arten durch Modalitätswechsel und gleichsinnige Inhaltsänderung.
Folgerungen durch formale Äquipollenz (formale Gleichwertung) sind solche, bei denen aus einem gegebenen Urteil bei gleicher Stellung der materialen Urteilsglieder ein Urteil abgeleitet wird, das von dem Grundurteil nur seiner Form nach verschieden ist. Spezielle Fälle solcher Folgerungen sind[12]:
1. Die Ableitung eines mittelbar bejahenden Urteils durch doppelte Verneinung aus einem unmittelbar bejahenden und umgekehrt (z. B. Grundurteil: S ← P; Folgerungsurteil: S ← nicht non-P; Grdurt.: jedes S ← P; Flgsurt.: kein S ← nicht-P; Grdurt.: S ← P, wenn Q ← R; Flgsurt.: S ← nicht P, wenn Q ← nicht R).
2. Die Ableitung einer mittelbaren Verneinung aus dem unmittelbar verneinenden Urteil und umgekehrt (z. B. Grdurt.: S ← nicht P; Flgsurt.: S ← non-P).
3. Die Ableitung einer apodiktischen Beurteilung aus einem unmittelbar gewissen Urteil (Grdurt.: 2 × 2 = 4; Flgsurt.: 2 × 2 ist notwendig 4).
4. Die Ableitung eines allgemeinen aus dem generellen Urteil und umgekehrt (Grdurt.: „Gestrenge Herren regieren nicht lange“; Flgsurt.: „kein gestrenger Herr regiert lange“).
5. Die Ableitung eines hypothetischen aus einem disjunktiven Gefüge (Grdurt.: S ← [entweder P1 oder P2]; Flgsurt.: wenn S ← P1, dann nicht S ← P2 usw.).
Wichtiger als die Folgerungen durch formale Äquipollenz sind die durch Konversion (Umkehrung). Sie bestehen darin, daß das Folgerungsurteil durch Vertauschung der materialen Glieder des Grundurteils[S. 74] gewonnen wird, wobei die Qualität der Aussage bestehen bleibt. Jenachdem ob die quantitative Bestimmtheit des Subjekts im Folgerungsurteil dieselbe bleibt wie im Grundurteil oder sich verändert, nennt man die Konversion eine reine (conversio pura, simplex) oder unreine bzw. veränderte (conversio impura, per accidens). — Folgerungen durch reine Umkehrung sind möglich:
1. aus partikulär bejahenden Urteilen (Grdurt.: „einige Säugetiere leben im Wasser“, Flgsurt.: „einige im Wasser lebende Tiere sind Säugetiere“).
2. aus allgemein verneinenden Urteilen (Grdurt.: „kein Sterblicher ist allwissend“, Flgsurt.: „kein Allwissender ist ein Sterblicher“).
Keinerlei denknotwendige Folgerungen durch Umkehrung sind möglich aus partikulär verneinenden, während allgemein bejahende Urteile Folgerungen teils durch reine, teils durch unreine Umkehrung zulassen. Beispiele von Folgerungen durch unreine Umkehrung aus allgemein bejahenden Urteilen sind: Grdurt.: „alle Wissenschaften sind Zeichen des menschlichen Dranges nach Erkenntnis“; Flgsurt.: „einige Zeichen des menschlichen Dranges nach Erkenntnis sind die Wissenschaften“. Beispiele von Folgerungen durch reine Umkehrung aus allgemein bejahenden Urteilen bieten die sog. reziprokablen Urteile, die Gleichungen oder Definitionen enthalten: Grdurt.: „alle Dreiecke von gleicher Höhe und Grundseite sind flächengleich“; Flgsurt.: „alle flächengleichen Dreiecke haben gleiche Grundseite und Höhe“. — Eine besondere Besprechung verlangen die Folgerungen durch Konversion aus hypothetischen Gefügen. Hypothetische Gefüge heißen rein umkehrbar, wenn ihre modale Bestimmtheit dieselbe bleibt, unrein umkehrbar, wenn diese sich verändert. Rein umkehrbar sind:
1. alle hypothetischen Gefüge, die unmittelbar oder mittelbar gewisse Gültigkeit haben (Grdurt.: „wenn in einem Dreieck zwei Winkel einander gleich sind, so ist es gleichschenklig“; Flgsurt.: „wenn ein Dreieck gleichschenklig ist, so sind darin zwei Winkel einander gleich“).
2. alle hypothetischen Gefüge über Tatsachen, die Gefüge ausschließlicher Konsequenz bilden (Grdurt.: „nur wenn ein luftleerer Raum hergestellt ist, fallen Körper verschiedenen Gewichts mit gleicher Geschwindigkeit“; Flgsurt.: „wenn Körper verschiedenen Gewichts mit gleicher Geschwindigkeit fallen, so ist der Raum, in dem das geschieht, luftleer“).
3. alle Verneinungen von hypothetischen Gefügen über Tatsachen (z. B. Grdurt.: „wenn ein Mensch behauptet, Gott zu sein, dann ist er nicht bei Verstand“; Flgsurt.: „wenn ein Mensch bei Verstand ist, dann behauptet er nicht, Gott zu sein“).
Unrein umkehrbar sind schließlich hypothetische Gefüge über Tatsachen wie: Grdurt.: „Wer nichts wagt, der nichts gewinnt“; Flgsurt.: „wer nichts gewinnt, der wagt möglicherweise nichts“. Hier hat die Konversion die Form: Grdurt.: wenn G, dann F, Flgsurt.: wenn F, dann möglicherweise G; in ihr geht also die assertorische Modalität des Grundurteils im Folgerungsurteil in eine problematische über.
[S. 75]
Aus dem Verfahren der formalen Äquipollenz und Konversion zusammengesetzt ist die Folgerungsweise durch Kontraposition (Umwendung). Diese geschieht, indem die materialen Glieder des Grundurteils miteinander die Stelle wechseln und die bejahenden Urteile ihrer Form nach verneinende, die verneinenden ihrer Form nach bejahende werden. Folgerungen durch Kontraposition sind rein möglich: 1. aus allgemein bejahenden Urteilen (Grdurt.: „alle Werke Schopenhauers sind stilistisch gewandt geschrieben“; Flgsurt.: „keine stilistisch ungewandte Schrift ist ein Werk Schopenhauers“); 2. aus partikulär verneinenden Urteilen (Grdurt.: „manche Völker Asiens sind in der Kultur nicht mitfortgeschritten“; Flgsurt.: „ein Teil der in der Kultur nicht mitfortgeschrittenen sind die Völker Asiens“). Nur unrein oder verändert sind Folgerungen durch Kontraposition möglich aus allgemein verneinenden Urteilen; während sich aus partikulär bejahenden Urteilen keinerlei denknotwendige Folgerungen herleiten lassen:
Allgemein verneinende Urteile gehen durch Kontraposition in partikuläre ihrer Form nach bejahende Urteile über (Grdurt.: „kein Verbrecher ist ein nützliches Mitglied der menschlichen Gesellschaft“; Flgsurt.: „ein Teil der unnützen Glieder der menschlichen Gesellschaft sind die Verbrecher“). — Nur geringe Bedeutung kommt den Folgerungen durch Kontraposition aus hypothetischen Gefügen zu. Hier herrschen analoge Verhältnisse vor wie bei den Folgerungen aus hypothetischen Gefügen durch Konversion. Als Beispiele solcher seien aufgeführt: 1. Grdurt.: „wenn Zahlen durch zwei teilbar sind, dann sind sie gerade Zahlen“; Flgsurt.: „wenn Zahlen ungerade sind, dann sind sie durch zwei nicht teilbar“ (reine Kontraposition); 2. Grdurt.: „wenn das Leben nach dem Tode paradiesisch ist, dann ist der Tod ein Beglücker der Menschheit“; Flgsurt.: „wenn es falsch ist, daß der Tod kein Beglücker der Menschheit ist, dann kann das Leben nach dem Tode paradiesisch sein“ (unreine Kontraposition).
Auf anderem Wege als bei den Folgerungen durch Konversion und Kontraposition kommen die Folgerungen durch Subalternation (Umordnung) zustande. Diese sind denknotwendige Ableitungen aus einem als wahr oder falsch beurteilten allgemeinen oder partikulären Urteil, dessen quantitative Bestimmtheit im Folgerungsurteil verändert, dessen Qualität aber dieselbe bleibt. Wenn es wahr ist, daß alle S ← P sind, dann ist es auch wahr, daß einige S ← P sind; und wenn es wahr ist, daß kein S ← P ist, dann ist es auch wahr, daß einige S ← nicht P sind. Wir nennen diese Ableitung von partikulären Urteilen aus allgemeinen Folgerungen durch Unterordnung,[S. 76] und können — da aus der Falschheit eines allgemeinen Urteils auf die Falschheit des ihm untergeordneten partikulären nicht denknotwendig geschlossen werden kann — sagen: Die Folgerungen aus der Wahrheit eines allgemeinen Urteils auf die Wahrheit des ihm untergeordneten sind gültig, die gleichen Folgerungen aus der Falschheit ungültig (in scholastischer Sprache bezeichnet als „Dictum de omni et nullo“)[13]. — Umgekehrt verhalten sich die Dinge bei den Folgerungen durch Überordnung (d. h. den Ableitungen allgemeiner aus partikulären Urteilen). Wenn es falsch ist, daß einige S ← P sind, dann ist es auch falsch, daß alle S ← P sind; und wenn es falsch ist, daß einige S ← nicht P sind, dann ist es auch falsch, daß alle S ← nicht P sind. Wir können also — da aus der Wahrheit eines partikulären Urteils auf die Wahrheit des entsprechenden übergeordneten nicht denknotwendig geschlossen werden kann — sagen: Die Folgerungen aus der Falschheit eines partikulären Urteils auf die Falschheit des ihm übergeordneten sind gültig, die gleichen Folgerungen aus der Wahrheit ungültig. Beide Gesetze kurz zusammengefaßt: Gültige Ableitungen durch Subalternation sind die Folgerungen durch Unterordnung aus der Wahrheit, durch Überordnung aus der Falschheit.
Den Folgerungen durch Subalternation verwandt sind die Folgerungen durch Opposition (Entgegensetzung). Darunter versteht man solche unmittelbaren Schlüsse, durch die aus der Wahrheit (oder Falschheit) eines quantitativ bestimmten Urteils auf die Falschheit (oder Wahrheit) des entsprechenden Urteils von entgegengesetzter Qualität gefolgert wird. Vorerst ist hierbei folgendes zu bemerken: Die Urteile: „alle S ← P“ und „einige S ← nicht P“, sowie: „kein S ← P“ und „einige S ← P“ heißen nach alter logischer Tradition kontradiktorisch-entgegengesetzte; die Urteile: „alle S ← P“ und „alle S ← nicht P“ konträr-entgegengesetzte und die Urteile: „einige S ← P“ und „einige S ← nicht P“ subkonträr-entgegengesetzte. Unter Zugrundelegung dieser Bezeichnungen ergibt sich: Wenn eines der Urteile „alle S ← P“ und „kein S ← P“ als wahr (oder falsch) gegeben ist, dann ist das ihnen kontradiktorisch-entgegengesetzte Urteil „einige S ← nicht P“ bzw. „einige S ← P“ falsch (oder wahr). Diese[S. 77] Tatsachen folgen unmittelbar aus den logischen Grundsätzen des Widerspruches und vom ausgeschlossenen Dritten. Danach können wir sagen: Die Folgerungen durch kontradiktorische Opposition sind durchweg gültig. Nicht ebenso liegen die Dinge bei den Folgerungen durch konträre und subkonträre Opposition. Wenn das Urteil „alle S ← P“ wahr ist, dann ist das Urteil „alle S ← nicht P“ falsch; wenn das Urteil „alle S ← P“ aber falsch ist, dann braucht es darum noch nicht wahr zu sein, daß „alle S ← nicht P“ sind. Mithin können wir sagen: Die Folgerungen durch konträre Opposition sind nur gültig aus der Wahrheit. Und weiter: Wenn es falsch ist, daß „einige S ← P“ sind, dann ist es wahr, daß „einige S ← nicht P“ sind; wenn es aber wahr ist, daß „einige S ← P“ sind, dann braucht es deswegen noch nicht falsch zu sein, daß „einige S ← nicht P“ sind. Die Folgerungen durch subkonträre Opposition sind also nur gültig aus der Falschheit. Alle drei Regeln kurz zusammengefaßt, gewinnen wir die logische Formel: Gültige Ableitungen sind die Folgerungen durch kontradiktorische Opposition aus der Wahrheit und Falschheit, durch konträre Opposition aus der Wahrheit und subkonträre Opposition aus der Falschheit.
Nur kurzer Besprechung bedürfen noch die unmittelbaren Schlüsse durch Modalitätswechsel und durch gleichsinnige Inhaltsänderung. Wenn es notwendig ist, daß S ← P ist, dann ist es auch Tatsache, daß S ← P ist; und wenn es nicht möglich ist, daß S ← P ist, dann ist es auch tatsächlich nicht der Fall usw. Mit Worten: Aus der Gültigkeit des apodiktischen Urteils folgt durch Modalitätswechsel die Gültigkeit des entsprechenden assertorischen und problematischen; aus der Ungültigkeit des problematischen Urteils folgt die Ungültigkeit des entsprechenden assertorischen und apodiktischen. — Und endlich: Folgerungen durch gleichsinnige Inhaltsänderung kommen zustande, wenn die materialen Glieder eines Urteils in gleichem Sinne inhaltlich verändert werden. Um das an Beispielen zu erläutern: Grdurt.: Alles Denken ist Urteilen oder Fragen; Flgsurt.: alles wissenschaftliche Denken ist wissenschaftliches Urteilen oder Fragen; Grdurt.: die Geschichte eines Volkes ist ein Spiegel seiner Entwicklung; Flgsurt.: die Kulturgeschichte eines Volkes ist ein Spiegel seiner kulturellen Entwicklung.
Mittelbare Schlüsse (oder Schlüsse im eigentlichen Sinne) sind solche, in denen aus einer Mehrheit gegebener Urteile ein davon verschiedenes denknotwendig abgeleitet wird. Die Urteile, aus denen abgeleitet wird, nennen wir Grundurteile oder Prämissen (die[S. 78] traditionelle Logik nennt sie grammatisierend „Vordersätze“), das Urteil, das abgeleitet wird, Schlußurteil oder Konklusio (Schlußsatz). Wo mittelbare Schlüsse nicht mehr als zwei Prämissen haben, nennt man die eine die obere (Obersatz), die andere die untere (Untersatz). So ist z. B. in dem Schlußverfahren: „Alle Körper ziehen einander an; Erde und Mars sind Körper; also ziehen Erde und Mars einander an“ das allgemeine Urteil: „alle Körper ziehen einander an“ die obere Prämisse (Obersatz), das spezielle Urteil: „Erde und Mars sind Körper“ die untere Prämisse (Untersatz) und das Endurteil: „also ziehen Erde und Mars einander an“ die Konklusio (Schlußsatz). Es ist ohne weiteres ersichtlich, daß nicht beliebig gewählte Urteile Prämissen für einen Schluß bilden können. Ein Schluß ist nur möglich, wenn die Grundurteile eine bestimmte logische Beziehung zueinander haben, oder genauer gesagt: einen denknotwendigen Zusammenhang untereinander herleiten. So wird z. B. in dem angeführten Beispiel ein denknotwendiger Zusammenhang hergestellt durch den in beiden Grundurteilen als gemeinsames materiales Glied enthaltenen Begriff „Körper“, indem zunächst ein allgemeines Gesetz über die Anziehung von Körpern aufgestellt, dann Erde und Mars als der Gattung Körper zugehörig bezeichnet und daraus geschlossen wird, daß Erde und Mars als Körper aufeinander nach dem Gesetz der Anziehung aller Körper einwirken. Auch hier wiederum liegen die Dinge so, daß die Gültigkeit des Schlußurteils — die formal-gültige Ableitung vorausgesetzt — mit der Gültigkeit der Prämissen steht und fällt.
Jenachdem ein Schluß von einem allgemeinen Urteil als Obersatz zu einem besonderen Urteil als Schlußsatz oder aber von besonderen Urteilen als Prämissen zu einem allgemeinen als Konklusio übergeht, nennt man ihn einen Schluß entweder vom Allgemeinen aufs Besondere oder vom Besonderen aufs Allgemeine. Zu diesen zählt die überlieferte Logik noch eine dritte Art von Schlüssen: die vom Besonderen aufs Besondere. Nach herkömmlicher Weise bezeichnet man die Schlüsse vom Allgemeinen aufs Besondere als deduktive oder Deduktionen, die Schlüsse vom Besonderen aufs Allgemeine als induktive oder Induktionen und die Schlüsse vom Besonderen aufs Besondere als Schlüsse per analogiam oder Analogieschlüsse.
Besprechen wir zunächst die deduktiven Schlüsse. Die überlieferte Lehre von den Schlußformen teilt die Deduktionen in die drei Hauptarten der kategorischen, hypothetischen und disjunktiven Schlüsse.[S. 79] Beispiele dafür sind: 1. Kategorischer Schluß: „Alle Römer waren kriegerisch; Cäsar war ein Römer; also war Cäsar kriegerisch“; 2. hypothetischer Schluß: „Wenn Cäsar ein Römer war, war er kriegerisch; Cäsar war ein Römer; also war Cäsar kriegerisch“; 3. disjunktiver Schluß: „Soldaten sind entweder tapfer oder keine Soldaten; Cäsar war tapfer; also war Cäsar ein Soldat.“ Diese Einteilung besteht jedoch nicht zu Recht. Es wird sich zeigen, daß die disjunktiven Schlüsse den kategorischen und hypothetischen nicht schlechthin koordiniert werden dürfen, da sie nicht wie diese einfach, sondern eigentümliche Zusammensetzungen von kategorischen und hypothetischen Schlüssen bilden. Demnach sind die deduktiven Schlüsse einzuteilen in einfache Deduktionen und Zusammensetzungen von solchen. Einfache Deduktionen sind teils die von der elementaren Form der eben erwähnten kategorischen Schlüsse (wir nennen sie kategorische oder elementare Deduktionen oder mit Aristoteles Syllogismen), teils die angeführten hypothetischen Schlüsse; Zusammensetzungen von deduktiven Schlüssen, sog. Ketten, sind teils reinliche, d. h. solche, die nur aus kategorischen Deduktionen gebildet sind, teils gemischte, d. h. solche, deren Analyse sowohl kategorische wie hypothetische Schlüsse als Bestandteile aufweist. Ordnen wir die Arten der deduktiven Schlüsse in einem übersichtlichen Schema, dann ergibt sich:
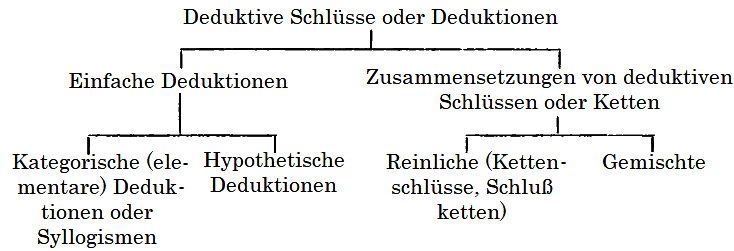
Erörtern wir fürs erste die Arten der kategorischen Deduktion. Als solche unterscheidet man nach Aristotelischem Vorbilde drei gültige Formen, die man von alters her als syllogistische Figuren (figurae Aristotelicae) bezeichnet[14]. Diese sind nach ihrer allgemeinsten Form:
[S. 80]
|
I. Figur:
|
II. Figur:
|
III. Figur:
|
|
|
Obers.:
|
Alle M ← P
|
Kein P ← M
|
Alle M ← P
|
|
Obers.:
|
Alle S ← M
|
Alle S ← M
|
Alle M ← S
|
|
Schlußs.:
|
Alle S ← P
|
Kein S ← P
|
Einige S ← P
|
Die materialen Bestandteile sind in allen drei Schlußformen dieselben: S, P und M, wobei M dasjenige Urteilselement bildet, das als beiden Prämissen gemeinsam den denknotwendigen Zusammenhang herstellt, aus welchem das Schlußurteil folgt. Man nennt dieses daher den Mittelbegriff (terminus medius), die beiden anderen materialen Glieder des Schlusses, die übereinstimmend in allen drei Figuren das Subjekt und Prädikat des Schlußurteils bilden, die äußeren Begriffe (termini externi). Von der Stellung des Mittelbegriffes in den Prämissen hängt die Einteilung der kategorischen Deduktionen ab. In der ersten Figur ist der Mittelbegriff Subjekt des Obersatzes und Prädikat des Untersatzes, in der zweiten Prädikat und in der dritten Subjekt beider Prämissen. Will man sich die Arten der Syllogismen hiernach durch ein einfaches Hilfsmittel der Anschauung mnemotechnisch näher bringen, so kann man die Stellung des Mittelbegriffes durch einen Pfeil symbolisieren, woraus das Bild entsteht:
|
I. Figur:
|
II. Figur:
|
II. Figur:
|
|
IV.(überflüssige)
Figur |
|
Zusammen-
fassung: |
|
|
O.:
|
M ← P
|
P ← M
|
M ← P
|
P ← M
|
|
||
|
U.:
|
S ← M
|
S ← M
|
M ← S
|
M ← S
|
|||
|
S.:
|
S ← P
|
S ← P
|
S ← P
|
S ← P
|
|||
|
(Pfeil schräg
von rechts unten nach links oben |
(Pfeil rechts,
nach oben |
(Pfeil links,
nach oben |
|||||
Der Mittelbegriff ist bildlich gesprochen die Seele des syllogistischen Schlußverfahrens. Ohne Mittelbegriff kein syllogistischer Schluß; und jeder Syllogismus wird zum Fehlschluß (Paralogismus), in dem mit dem Mittelbegriff in den beiden Prämissen nicht ein und derselbe Inhalt gedacht wird. Nach der Bedeutung des Mittelbegriffes können wir den Syllogismus auch definieren als dasjenige Schlußverfahren, in dem aus zwei Urteilen, die eines ihrer materialen Glieder gemeinsam haben, ein drittes über deren nichtgemeinsame Bestandteile notwendig abgeleitet wird.
[S. 81]
Besprechen wir die syllogistischen Figuren im einzelnen:
I. Als Grundform der ersten syllogistischen Figur haben wir genannt: M ← P; S ← M; also S ← P. Diese Grundform hat vier Modifikationen:
|
I. Figur:
|
a)
|
b)
|
c)
|
d)
|
|
Alle M ← P
|
Alle M ← P
|
Kein M ← P
|
Kein M ← P
|
|
|
Alle S ← M
|
Einige S ← M
|
Alle S ← M
|
Einige S ← M
|
|
|
Alle S ← P
|
Einige S ← P
|
Kein S ← P
|
Einige S ← nichtP
|
|

|

|
|||
Es ist ohne weiteres ersichtlich, daß in dieser Aufstellung die Modifikationen a und b sowie c und d zusammengehören. Wir können sagen: a und b machen die erste, c und d die zweite Schlußweise der ersten Figur aus. Der Gedankengang der ersten Schlußweise ist folgender: Wenn einem Subjekt S das Prädikat M zukommt, dem Prädikat M ein Prädikat P, so kommt auch dem Subjekt S mittelbar das Prädikat P zu. Demnach können wir als logisches Prinzip der ersten Schlußweise der ersten Figur den Grundsatz aufstellen: Jedem Subjekt kommt mittelbar das Prädikat seines Prädikats zu. Der Gedankengang der zweiten Schlußweise der ersten Figur ist dem der ersten analog: wenn einem Subjekt S ein Prädikat M zukommt, ein Prädikat P von diesem M aber ausgeschlossen ist, so ist dieses P auch von S ausgeschlossen. Als logisches Prinzip der zweiten Schlußweise der ersten Figur können wir mithin schreiben: Keinem Subjekt kommt mittelbar als Prädikat zu, was nicht Prädikat eines Prädikats von ihm ist. — Als spezielle Bedingungen des Schlußverfahrens der ersten Figur lassen sich folgende zusammenstellen: 1. Die obere Prämisse muß allgemein sein, kann jedoch bejahend oder verneinend sein; 2. die untere Prämisse kann allgemein oder partikulär, muß jedoch bejahend sein. (Sind beide Prämissen negativ, so ist überhaupt kein Schluß möglich.) 3. Der Subjektsumfang des Schlußurteils richtet sich nach dem der unteren Prämisse, seine Qualität nach der der oberen. Beispiele der beiden Schlußweisen der ersten Figur sind:
|
I a.
|
I c.
|
|
Alle Säugetiere atmen durch Lungen.
|
Kein Inhalt des Bewußtseins ist als
solcher der Seele angeboren. |
|
Alle Walfische sind Säugetiere.
|
Alle Begriffe sind Inhalte des
Bewußtseins. |
|
Alle Walfische atmen durch Lungen.
|
Kein Begriff ist der Seele angeboren.
|
(Entsprechende Beispiele für die Modifikationen b und d ergeben sich leicht.)
II. Die Grundform der zweiten syllogistischen Figur lautet: P ← M; S ← M; also S ← P. In ihren Modifikationen ergibt sie folgendes Bild:
|
II. Figur:
|
a)
|
b)
|
c)
|
d)
|
|
Kein P ← M
|
Kein P ← M
|
Alle P ← M
|
Alle P ← M
|
|
|
Alle S ← M
|
Einige S ← M
|
Kein S ← M
|
Einige S ← nicht M
|
|
|
Kein S ← P
|
Einige S ← nicht P
|
Kein S ← P
|
Einige S ← nichtP
|
|

|

|
|||
[S. 82]
Auch hier sind a und b gültige Möglichkeiten einer ersten, c und d gültige Möglichkeiten einer zweiten Schlußweise. Der Gedankengang der ersten ist: Wenn einem Subjekt S das Prädikat M zukommt, einem Subjekt P dasselbe Prädikat M aber nicht, dann kann P als Prädikat nicht dem Subjekt S zukommen. Als logisches Prinzip der ersten Schlußweise der zweiten Figur ergibt sich also der Grundsatz: Keinem Subjekt kommt mittelbar ein Prädikat zu, von dem ein dem Subjekt zukommendes Prädikat allgemein ausgeschlossen ist. Der Gedankengang der zweiten Schlußweise lautet: Wenn einem Subjekt S ein Prädikat M nicht zukommt, das einem Subjekt P nach seinem ganzen Umfange zukommt, dann kann P nicht Prädikat von S sein. Als logischer Grundsatz der zweiten Schlußweise der zweiten Figur ausgesprochen: Keinem Subjekt kommt mittelbar ein Prädikat zu, von dem ein dem Subjekt nicht zukommendes Prädikat allgemein gilt. — Die speziellen Bedingungen möglicher Schlußweisen der zweiten Figur sind: 1. Die obere Prämisse muß allgemein, kann aber verneinend oder bejahend sein; 2. die untere Prämisse kann allgemein oder partikulär, muß aber in ihrer Qualität der der oberen Prämisse entgegengesetzt sein. (Sind beide Prämissen bejahend oder beide verneinend, so ist nach der zweiten Figur überhaupt kein Schluß möglich.) 3. Das Schlußurteil ist stets negativ; sein Subjektsumfang richtet sich nach dem der unteren Prämisse. Um wiederum Beispiele zu geben:
|
II a.
|
II c.
|
|
Keine wissenschaftlich-begründete Weltauffassung
dient ausschließlich dazu, die Gemütsbedürfnisse des Menschen
zu befriedigen.
|
Alle brauchbaren Mitglieder des
Staates gehorchen den Gesetzen.
|
|
Alle Religionen dienen ausschließlich
diesem Zwecke.
|
Kein revolutionär gesinnter Geist gehorcht
den Gesetzen.
|
|
Keine Religion ist eine wissenschaftlich-begründete
Weltauffassung.
|
Kein revolutionär gesinnter Geist ist
ein brauchbares Mitglied des Staates.
|
(Man ergänze hierzu die Beispiele für die Modifikationen b und d.)
III. Die Grundform der dritten syllogistischen Figur heißt: M ← P; M ← S; also S ← P. Entwickeln wir diese in ihren Modifikationen, dann ergibt sich:
| III. Fig.: |
|
a)
|
b)
|
c)
|
|
Alle M ← P
|
Alle M ← P
|
Einige M ← P
|
||
|
Alle M ← S
|
Einige M ← S
|
Alle M ← S
|
||
|
Einige S ← P
|
Einige S ← P
|
Einige S ← P
|
||

|
|
|||
|
d)
|
e)
|
f)
|
||
|
Kein M ← P
|
Kein M ← P
|
Einige M ← nicht P
|
||
|
Alle M ← S
|
Einige M ← S
|
Alle M ← S
|
||
|
Einige S ← nicht P
|
Einige S ← nicht P
|
Einige S ← nicht P
|
||

|
|
|||
[S. 83]
Hier zeigt sich leicht, daß a und b die erste, c die zweite, d und e die dritte und f die vierte selbständige Schlußweise bilden. Der Gedankengang der ersten Schlußweise ist: Wenn alle M P sind und alle (oder auch nur einige) M außerdem S, dann kommt notwendig denjenigen S, die M sind, also einigen S gleichfalls P zu. In Worten — als logischer Grundsatz der ersten Schlußweise der dritten Figur — formuliert: Jedem Subjekt (S), das wiederum Prädikat eines Subjekts (M) ist, welches durch ein anderes Prädikat (P) allgemein bestimmt wird, kommt mittelbar auch dieses andere Prädikat (P) zu. Analysieren wir den Gedankengang der zweiten Schlußweise: Wenn alle M S sind und einige M P, dann sind notwendig einige der S, und zwar diejenigen, die M sind, auch P. Als logischen Grundsatz der zweiten Schlußweise der dritten Figur dürfen wir demnach schreiben: Jedem Subjekt (S), das wiederum allgemeines Prädikat eines Subjekts (M) ist, welches durch ein anderes Prädikat (P) partikulär bestimmt wird, kommt mittelbar auch dieses andere Prädikat (P) zu. Die dritte Schlußweise enthält folgenden Gedankengang: Wenn alle oder einige M S sind, kein M aber P, dann sind notwendig diejenigen S, die M sind, also einige S nicht P. Der Grundsatz der dritten Schlußweise der dritten Figur lautet also: Keinem Subjekt (S), das zugleich Prädikat eines Subjekts (M) ist, von dem ein anderes Prädikat (P) allgemein ausgeschlossen ist, kommt mittelbar dieses andere Prädikat zu. Und endlich die vierte Schlußweise: Wenn alle M S sind, einige M aber nicht P, dann sind notwendig diejenigen S, die M sind, also einige S nicht P. Mithin ergibt sich als Grundsatz der vierten Schlußweise der dritten Figur: Keinem Subjekt (S), das zugleich allgemeines Prädikat eines Subjekts (M) ist, von dem ein anderes Prädikat (P) partikulär ausgeschlossen ist, kommt mittelbar dieses andere Prädikat zu. — Als spezielle Bedingungen möglicher Schlußweisen der dritten Figur müssen gelten: 1. Die obere Prämisse kann allgemein oder partikulär, bejahend oder verneinend sein; 2. die untere Prämisse muß allgemein, wenn die obere partikulär, kann aber sowohl partikulär wie allgemein sein, wenn die obere allgemein ist (sind beide Prämissen partikulär, so ist überhaupt kein Schluß möglich); ferner muß die untere Prämisse stets bejahend sein; 3. das Schlußurteil ist stets partikulär, seine Qualität richtet sich nach der der oberen Prämisse. Beispiele der vier Schlußweisen der dritten Figur sind:
|
III a.
|
III c.
|
|
Alle Regungen des Neides und der Mißgunst sind
verwerflich.
|
Einige Christen tun Sünde.
|
|
Alle Regungen des Neides und der Mißgunst sind
Affekte.
|
Alle Christen sind gottesfürchtig.
|
|
Einige Affekte sind verwerflich.
|
Einige Gottesfürchtige tun Sünde.
|
|
III d.
|
III f.
|
|
Keine Rose ist frei von Dornen.
|
Einige Chroniken des Mittelalters sind
nicht erhalten.
|
|
Alle Rosen sind Zierpflanzen.
|
Alle Chroniken des Mittelalters sind
wertvolle historische Dokumente.
|
|
Einige Zierpflanzen sind nicht frei
von Dornen.
|
Einige wertvolle historische Dokumente
des Mittelalters sind nicht erhalten.
|
(Man suche auch hier entsprechende Beispiele für III b und III e.)
[S. 84]
Die oben erwähnte vierte syllogistische Figur wurde zuerst von Galenus (um 150 n. Chr. Geb.) den Aristotelischen hinzugefügt; man nennt sie aus diesem Grunde die Galenische Schlußweise. Sie ist, wie bereits betont, keine selbständige Form des Schließens, sondern läßt sich auf die Modifikationen der Aristotelischen Syllogismen zurückführen. Tatsächlich pflegt das Denken sich ihrer nicht zu bedienen; und alle Logik, die sie aus formalistischen Gründen den drei Aristotelischen Figuren als vierte nebenordnet, tut den normalen Verhältnissen des Schließens Zwang an. Das braucht nur an ihrer Grundform: Alle P ← M; alle M ← S; also einige S ← P gezeigt zu werden. Als Beispiel dafür diene: „Alle Strafgefängnisse sind Besserungsanstalten; alle Besserungsanstalten sind soziale Institutionen: also: einige soziale Institutionen sind Strafgefängnisse.“ Der natürliche Verlauf des Denkens pflegt nicht so vorzugehen, sondern vielmehr aus den gegebenen Prämissen nach der ersten Aristotelischen Figur das Schlußurteil abzuleiten: „Alle Strafgefängnisse sind soziale Institutionen.“ Daraus ergibt sich in unmittelbarer Folgerung durch conversio impura das Urteil: „Einige soziale Institutionen sind Strafgefängnisse.“ (Über die Zurückführbarkeit der modifizierten Formen der Galenischen Figur auf die Aristotelischen Syllogismen vgl. B. Erdmann, Logik I2 S. 677 ff.)
Einer besonderen Erwähnung bedürfen diejenigen Syllogismen, in denen beide Prämissen und demzufolge auch die Konklusio aus Relationsurteilen bestehen. Hierhin gehören z. B. viele mathematische Schlüsse (auch die Formen des Rechnens), ferner alle diejenigen Deduktionen, in denen aus dem Verhältnis der Gleichheit, Ähnlichkeit oder Verschiedenheit zweier Gegenstände zu einem dritten auf die Gleichheit, Ähnlichkeit oder Verschiedenheit untereinander geschlossen wird (Grundform: S = M, M = P, also S = P). In diesen Formen ist der Mittelbegriff M der gemeinsame Beziehungspunkt, zu dem die materialen Glieder des Schlußurteils (S und P) in Relation gesetzt werden. Ihr logisches Prinzip ist also: Stehen zwei Begriffe zu einem dritten unmittelbar in logischer Relation, so stehen sie mittelbar auch untereinander in einer solchen. Daß es sich hier um Syllogismen handelt, kann nicht in Zweifel gezogen werden; wenngleich diese Formen von den oben besprochenen, deren Prämissen als Inhärenzurteile gedacht waren, charakteristisch abweichen. Man könnte jene geradezu Inhärenzsyllogismen, diese Relationssyllogismen nennen. Daß sie nicht, wie oben vom Syllogismus gesagt, Schlüsse vom Allgemeinen aufs Besondere bilden, beweist nicht, daß sie keine Syllogismen, wohl aber, daß die überlieferte Lehre, die im Syllogismus allemal einen Schluß vom Allgemeinen aufs Besondere sieht, einer Revision bedarf. — Als Beispiele der mannigfachen Formen von Relationssyllogismen seien hier aufgeführt:
[S. 85]
| 1. |
S = M
|
2. |
S ähnlich M
|
3. |
S größer als M
|
4. |
S früher als M
|
|
M = P
|
M ähnlich P
|
M größer als P
|
M früher als P
|
||||
|
S = P
|
S ähnlich P
|
S größer als P
|
S früher als P
|
| 5. |
S Ursache von M
|
6. |
S liegt südlich von M
|
7. |
S Vater von M
|
|
M Ursache von P
|
M liegt westlich von P
|
M Vater von P
|
|||
|
S Ursache von P
|
S lieg südwestlich von P
|
S Großvater P
|
Die gegebenen Ausführungen über die kategorischen Deduktionen beziehen sich durchgehends auf solche Fälle, in denen die Prämissen aus einfachen Urteilen gebildet sind. Demgegenüber muß betont werden, daß diese auch aus zusammengesetzten Urteilen, sowohl aus Beurteilungen wie Urteilsverbindungen und -gefügen, bestehen können. Die Schlußformen selbst erleiden dadurch keine Veränderung. Daß aus zwei verneinenden Beurteilungen als Grundurteilen kein Schluß möglich sei, ist bereits früher hervorgehoben worden. Sind beide Prämissen Beurteilungen apodiktischer Gültigkeit, dann ist auch das Schlußurteil apodiktisch; sind beide als assertorisch oder beide als problematisch beurteilt, dann hat auch das Schlußurteil assertorische oder problematische Modalität. Ist eine der Prämissen nur problematisch gültig, dann ist das Schlußurteil stets problematisch, selbst dann, wenn die andere Prämisse apodiktisch gilt. Und endlich: Ist die obere Prämisse tatsächlich, die untere notwendig gültig, dann ist das Schlußurteil assertorisch; ist jedoch die obere Prämisse notwendig, die untere tatsächlich gültig, dann kommt auch dem Schlußurteil apodiktische Modalität zu. Beispiele für diese Möglichkeiten ergeben sich dem, der ihrer bedarf, mit leichter Mühe.
Eine kurze Besprechung erfordern noch die Schlüsse, bei denen beide Prämissen hypothetische Gefüge sind. Sie sind Syllogismen, wenn sie (gleich den kategorischen Deduktionen aus einfachen Urteilen) drei materiale Bestandteile enthalten, deren einer das Mittelglied bildet (G = Grund; M = Mittelbegriff; F = Folge). Stellen wir bei ihrer Darstellung aus Gründen der Deutlichkeit die untere vor die obere Prämisse, dann ergibt sich folgendes Bild:
Syllogismen aus hypothetischen Prämissen:
|
I.
|
Figur:
|
a)
|
Wenn G, dann M
|
b)
|
Wenn G, dann M
|
|
Wenn M, dann F
|
Wenn M, dann F nicht
|
||||
|
Wenn G, dann F
|
Wenn G, dann F nicht
|
||||
|
[S. 86]
II.
|
Figur:
|
a)
|
Wenn G, dann M
|
b)
|
Wenn G, dann M nicht
|
|
Wenn F, dann M nicht
|
Wenn F, dann M nicht
|
||||
|
Wenn G, dann F nicht
|
Wenn G, dann F nicht
|
||||
|
III.
|
Figur:
|
a)
|
Wenn M, dann G
|
b)
|
Wenn M, dann G
|
|
Wenn M, dann F
|
Wenn M, dann F nicht
|
||||
|
Wenn G, dann möglicherweise F
|
Wenn G, dann möglicherweise F nicht
|
Bei der dritten Figur reduzieren sich die möglichen Schlußweisen aus hypothetischen Prämissen auf zwei, weil die Quantitätsverhältnisse, die bei den kategorischen Urteilen spezifische Unterschiede erzeugen, hier fortfallen. An deren Stelle treten, wie schon bei der Besprechung der Folgerungen durch Konversion erwähnt, Modalitätsunterschiede. Bei der dritten Figur z. B. sind aus hypothetischen Prämissen apodiktischer und assertorischer Gültigkeit nur problematische Schlußurteile ableitbar, während bei den beiden anderen syllogistischen Figuren aus hypothetischen Prämissen die apodiktische oder assertorische Modalität der Grundurteile unverändert auf das Schlußurteil übergeht. (Genaueres über diese Formen bei B. Erdmann, a. a. O., Kap. 81)
Von den Syllogismen aus hypothetischen Prämissen (als einer Unterart der kategorischen Deduktionen) sind streng zu scheiden die hypothetischen Deduktionen, die wir oben als zweite Art der einfachen deduktiven Schlüsse den elementaren Deduktionen entgegengesetzt haben. Hypothetische Deduktionen sind einfache Schlüsse, deren obere Prämisse ein hypothetisches Gefüge ist, während die untere Prämisse das eine Glied, das Schlußurteil das andere Glied dieses Gefüges enthalten, die darin entweder als gültig oder als ungültig beurteilt werden. Als Beispiel dieser diene zunächst ihre einfachste Form: „Wenn Q ← R, dann S ← P; nun Q ← R gültig; also S ← P gültig.“ Deduktive Schlüsse sind die hypothetischen Ableitungen, weil die obere Prämisse in der ausgesagten Beziehung von Grund und Folge eine Regel ausdrückt, aus der an der Hand der bejahenden oder verneinenden Beurteilung eines ihrer Glieder die Gültigkeit oder Ungültigkeit des anderen Gliedes des Gefüges geschlossen wird.
Entsprechend den in der Urteilslehre angeführten Grundformen hypothetischer Gefüge, von denen die vierte und letzte die Form der Verneinung hypothetischer Urteile darstellt [1. wenn G, dann F; 2. wenn G nicht, dann F; 3. wenn G nicht, dann F nicht;[S. 87] 4. wenn G, dann F nicht], ergeben sich folgende Hauptformen hypothetischer Deduktionen mit ihren Modifikationen, die man als „modi ponentes“ und „modi tollentes“ (setzende und aufhebende Möglichkeiten) bezeichnet:
|
a)
|
b)
|
|||||
|
I.
|
|
modus
ponens: |
Wenn
|
G, dann
F
|
Wenn
|
G nicht, dann
F
|
|
G ist wahr
|
|
G nicht, ist wahr
|
||||
|
|
F ist wahr
|
|
F ist wahr
|
|||
|
|
c)
|
d)
|
||||
|
Wenn
|
G nicht, dann
F nicht
|
Wenn
|
G, dann
F nicht
|
|||
|
G ist wahr
|
G ist wahr
|
|||||
|
|
F ist wahr
|
|
F nicht, ist wahr
|
|||
|
a)
|
b)
|
|||||
|
II.
|
|
modus
tollens: |
Wenn
|
G, dann
F
|
Wenn
|
G nicht, dann
F
|
|
F ist falsch
|
|
F ist falsch
|
||||
|
|
G ist falsch
|
|
G nicht, ist falsch
|
|||
|
|
c)
|
d)
|
||||
|
Wenn
|
G nicht, dann
F nicht
|
Wenn
|
G, dann
F nicht
|
|||
|
F ist falsch
|
F nicht, ist falsch
|
|||||
|
|
G ist falsch
|
|
G ist falsch
|
|||
Die Schlußweise der hypothetischen Deduktionen geht also immer von der Wahrheit des Grundes auf die Wahrheit der Folge, von der Falschheit der Folge auf die Falschheit des Grundes. Die Voraussetzung der Gültigkeit des Schlußurteils ist neben der formalgültigen Ableitung wie bei allen Schlüssen die Gültigkeit der Prämissen. Ist z. B. das hypothetische Gefüge der oberen Prämisse falsch, so kann auch das Schlußurteil falsch sein; und ganz dasselbe gilt, wenn die untere Prämisse des hypothetischen Schlusses falsch ist. — Als Beispiel der Grundformen des „modus ponens“ (I) und des „modus tollens“ (II) seien angeführt:
|
I a.
|
II a.
|
|
Wenn es tatsächlich wahr ist, daß Pythagoras den
nach ihm benannten Lehrsatz gefunden hat, dann muß er als ein
bedeutender Mathematikerangesehen werden.
|
Wenn der Reichtum eine Bedingung des
Glücks wäre, dann müßten die Menschen umso glücklicher sein, je
reicher sie sind.
|
|
Es ist tatsächlich wahr, daß Pythagoras
diesen Lehrsatz gefunden hat.
|
Es ist falsch, daß die Menschen umso glücklicher
sind, je reicher sie sind.
|
|
Pythagoras muß als ein bedeutender
Mathematiker angesehen werden.
|
Es ist falsch, daß Reichtum eine Bedingung des
Glücks ist.
|
[S. 88]
Die traditionelle Logik hat den kategorischen und hypothetischen Deduktionen den disjunktiven Schluß als dritte einfache Form der deduktiven Schlüsse koordiniert. Schon oben war dagegen zu betonen gewesen, daß diese Einteilung falsch ist, weil die disjunktiven Schlüsse nicht einfache, sondern gemischte Zusammensetzungen einfacher Schlüsse sind. Das sei hier näher begründet:
Unter einem disjunktiven Schluß versteht man im allgemeinen eine Ableitung, bei der die obere Prämisse ein disjunktives Gefüge, die untere die bejahende oder verneinende Beurteilung eines (oder mehrerer) Glieder dieses Gefüges und das Schlußurteil die verneinende oder bejahende Beurteilung der übrigbleibenden Glieder desselben Gefüges bilden. Beispiele ihrer Form nach sind dafür:
|
I.
|
|
modus
ponens: |
S ← [entweder P1 oder P2]
|
|
S ← P1 ist wahr
|
|||
|
S ← P2 ist falsch
|
|||
|
II.
|
|
modus
tollens: |
S ← [entweder P1 oder P2]
|
|
S ← P1 ist falsch
|
|||
|
S ← P2 ist wahr
|
An diesen Formen deutet schon der in den Prämissen scheinbar enthaltene Widerspruch darauf hin, daß der vorliegende Schluß verwickelter sei, als es nach dem gegebenen Buchstabenschema scheint: Wenn nämlich in der unteren Prämisse behauptet wird, daß S ← P1 wahr, in der oberen, daß S entweder P1 oder P2 sei, dann hebt das untere Grundurteil anscheinend die Gültigkeit des oberen auf, indem es als wahr behauptet, was dort nur als eine der möglichen, einander ausschließenden Prädizierungen gegeben ist. Analysieren wir daher den logischen Aufbau dieser Art Schlüsse an einem Beispiel genauer, dann ergibt sich:
|
Beispiel:
|
Form:
|
|||||
|
Alle Farbenblindheit ist entweder eine
partielle oder totale. |
|
|
Syllogismus
der I. Figur. |
Alle
|
Sm ← [entweder P1
oder P2]
|
|
|
Die Grünrotblindheit ist eine
Farbenblindheit. |
S ← Sm
|
|||||
|
Die Grünrotblindheit ist entweder
eine partielle oder totale Farbenblindheit. |
S ← [entweder
P1 oder P2]
|
|||||
|
Folgerung
durch formale Äquipollenz. |
||||||
|
Also: Wenn die Gr. eine part. F. ist,
dann ist sie keine totale |
|
also:
|
Wenn
dann |
S ← P1 wahr,
S ← P2 falsch |
||
|
und: Wenn die Gr. eine totale F. ist,
dann ist sie keine partielle. |
Hypothetischer
Schluß (modus ponens). |
und:
|
Wenn
dann |
S ← P2 wahr,
S ← P2 falsch |
||
|
Nun ist die Gr. eine partielle Farbenbl.
|
S ← P1 wahr
|
|||||
|
Die Grünrotblindheit ist keine totale
Farbenblindheit. |
S ← P2 falsch.
|
|||||
Daraus erweist sich, daß der sog. disjunktive Schluß keine einfache deduktive Form des Schließens bildet, sondern eine Zusammensetzung von Schlüssen, deren Elemente ein Syllogismus der ersten Figur, ein unmittelbarer [S. 89]Schluß durch formale Äquipollenz und eine hypothetische Deduktion sind. Disjunktive Schlüsse sind mithin (nach der früher entwickelten Scheidung) nicht reinliche, sondern gemischte Zusammensetzungen von Schlüssen. Bevor diese behandelt werden, sei zunächst den Arten der reinlichen Zusammensetzungen deduktiver Schlüsse eine kurze Besprechung gewährt.
Reinliche Zusammensetzungen deduktiver Schlüsse sind solche, die nur aus kategorischen Schlüssen zusammengesetzt sind; (reinliche Zusammensetzungen aus hypothetischen Schlüssen sind nach dem Wesen dieser nicht möglich). Die einfachste Form reinlicher Zusammensetzungen sind diejenigen Verbindungen von Schlüssen, in denen der Schlußsatz eines Syllogismus gleichzeitig den Obersatz eines anderen Syllogismus bildet; der in seiner Stellung vordere Syllogismus heißt dabei Prosyllogismus, der hintere Episyllogismus. Jenachdem die ganze Ableitung aus zwei, drei, vier oder mehr Syllogismen zusammengesetzt ist, heißt sie eine zwei-, drei-, vier- oder vielgliedrige Schlußkette (Polysyllogismus).
Von den Schlußketten scheidet man die sog. Kettenschlüsse (Sorites), die im Grunde jedoch lediglich verkürzte Schlußketten sind. In ihnen werden nämlich die Schlußsätze der einzelnen syllogistischen Glieder einfach übersprungen. Dem Verlauf des natürlichen Denkens stehen sie darum näher als die zuerst erwähnten Schlußketten. Zeigt doch dieses immer die Tendenz, das irgend Entbehrliche auszuscheiden und den Gesamtprozeß der Ableitung zu verkürzen. Nach alter logischer Tradition zerfallen die Kettenschlüsse in zwei Arten, deren erste man nach ihrem Entdecker den Aristotelischen, deren zweite man nach ihrem Entdecker Rudolf Goclenius, einem Marburger Philosophen aus den Jahren 1547-1628, den Goclenischen Sorites nennt. (B. Erdmann schlägt nach ihrem Wesen für den Goclenischen den Namen subsumierender, für den Aristotelischen den Namen analysierender Sorites vor.) Ihrer logischen Grundform nach sehen Schlußkette, Aristotelischer und Goclenischer Kettenschluß folgendermaßen aus:
|
I. Schlußketten:
|
|
|
a)
|
b)
|
|
Alle Ma ← P
|
Alle S ← Ma
|
|
Alle Mb ← Ma
|
Alle Ma ← Mb
|
|
Alle Mb ← P
|
Alle S ← Mb
|
|
Alle Mc ← Mb
|
Alle Mb ← Mc
|
|
Alle Mc ← P
|
Alle S ← Mc
|
|
Alle Md ← Mc
|
Alle Mc ← Md
|
|
Alle Md ← P
|
Alle S ← Md
|
|
Alle S ← Md
|
Alle Md ← P
|
|
Alle S ← P
|
Alle S ← P
|
|
II. Kettenschlüsse:
|
|
|
a)
|
b)
|
|
Goclenischer
Sorites. |
Aristotelischer
Sorites. |
|
Alle Ma ← P
|
Alle S ← Ma
|
|
Alle Mb ← Ma
|
Alle Ma ← Mb
|
|
Alle Mc ← Mb
|
Alle Mb ← Mc
|
|
Alle Md ← Mc
|
Alle Mc ← Mb
|
|
Alle S ← Md
|
Alle Md ← P
|
|
Alle S ← P
|
Alle S ← P
|
[S. 90]
Aus der Schlußkette a ist durch Ausfall der Schlußurteile der einzelnen Glieder der Goclenische, aus der Schlußkette b der Aristotelische Kettenschluß ableitbar. Darum gelten für beide Arten von Ketten die gleichen allgemeinen Regeln, deren wichtigste besagen: Das Schlußurteil einer Kette kann nur allgemein sein, wenn alle Prämissen allgemein sind, ist aber partikulär, sobald eine ihrer Prämissen partikuläre Quantität hat. Ferner: das Schlußurteil einer Kette kann nur bejahend sein, wenn alle ihre Prämissen bejahend sind, ist aber verneinend, wenn eine ihrer Prämissen negativ ist. Wie es Syllogismen aus beurteilenden, Syllogismen aus hypothetischen Grundurteilen gibt, so auch Schlußketten und Kettenschlüsse. Als Hauptformen der Kettenschlüsse aus hypothetischen Gefügen seien aufgeführt: 1. wenn G, dann M1; wenn M1, dann M2; wenn M2, dann M3; wenn M3, dann F; also: wenn G, dann F; 2. wenn G, dann M1; wenn M1, dann M2; wenn M2, dann M3; wenn M3, dann nicht F; also: wenn G, dann nicht F. Die Modalität des Schlußurteiles einer Kette ist problematisch, wenn eines ihrer Glieder ein problematisches Urteil ist. Formen von Schlußketten und Kettenschlüssen aus Relationsurteilen sind nach den oben angeführten Beispielen von Polysyllogismen leicht aufzustellen. (Ausführliches hierzu bei Drobisch, Neue Darstellung der Logik, 4. Aufl. 1875, § 105 ff.)
Die gemischten Zusammensetzungen deduktiver Schlüsse bedürfen nach den dargestellten Voraussetzungen keiner näheren Erörterung mehr. Schon oberflächliche Prüfung ergibt das Vorhandensein einer Mannigfaltigkeit von möglichen Verbindungen hypothetischer mit kategorischen Deduktionen, mit Schlußketten und Kettenschlüssen, zum Teil — wie bei den oben besprochenen disjunktiven Zusammensetzungen — solche, in denen außer mittelbaren Schlüssen deduktiver Konsequenz unmittelbare Schlüsse oder Folgerungen mit eingewebt sind. Als Beispiele gemischter Zusammensetzungen deduktiver Schlüsse seien ihrer Form nach noch aufgeführt:
|
I.
|
Wenn
|
Q ← R,
dann alle M ← P
|
|
Kettenschluß aus
hypothetischen Prämissen. |
|
|
Wenn
|
T ← V,
dann alle V ← W
|
||||
|
Wenn
|
V ← W,
dann alle X ← Y
|
||||
|
Wenn
|
X ← Y,
dann alle M ← P
|
||||
|
Wenn
|
Q ← R,
dann alle M ← P
|
|
Hypothetische Deduktion.
|
||
|
|
Alle Q ← R
wahr
|
|
|||
|
|
Alle M ← P
wahr
|
Syllogismus der ersten
Schlußweite der ersten Fig. |
|||
|
|
Alle S ← M
|
||||
|
|
Alle S ← P,
|
[S. 91]
|
II.
|
Wenn
|
alle Q ← R,
dann alle M ← P
|
|
Hypothetische Deduktion.
|
|
|
alle Q ← R
wahr
|
|||||
|
|
alle M ← P
wahr
|
|
Goclenischer Sorites mit
allgemein-bejahenden Pro- syllogismen u. partikulär- bejahendem, problematischem Episyllogismus. |
||
|
Alle Ma ← M
|
|||||
|
Alle Mb ← Ma
|
|||||
|
Alle Mc ← Mb
|
|||||
|
Einige O vielleicht ← Mc
|
|||||
|
Einige O vielleicht ← P
|
|
Syllogismus der zweiten
Schlußweite der dritten Fig. |
|||
|
Alle O ← S
|
|||||
|
Einige S vielleicht ← P
|
Wie es verkürzte Urteile gibt („Hilfe“; „Feuer“; die meisten Kommandorufe bei turnerischen und militärischen Übungen), so auch verkürzte Schlußformen, sog. Enthymeme — z. B.: „Alle Menschen sind bisher gestorben, also wird Schreiber dieser Zeilen auch sterben.“ Diese Verkürzungen — am häufigsten durch Ausfall einer Prämisse in einfachen Schlüssen oder Ketten, meistens der unteren Prämisse — betreffen indessen nicht den logischen Aufbau eines Schlusses, sondern psychologische Eigenheiten des Denkens oder grammatische Besonderheiten des sprachlichen Ausdruckes der Sätze. Ihre Erörterung gehört also nicht zu den Aufgaben der Logik.
Die logische Theorie des deduktiven Schließens hat Antwort zu geben auf die Frage: Welcher Art sind in den deduktiven Schlußweisen die Beziehungen zwischen den Prämissen und der Konklusio, genauer gesagt: die Beziehungen zwischen den einzelnen materialen Gliedern des ganzen Schlußverfahrens?
Bei den hypothetischen Deduktionen ergeben sich die hierher gehörigen Bestimmungen leicht. Sind im hypothetischen Gefüge die beiden Elemente im logischen Verhältnis von Grund und Folge zueinander gedacht, dann besteht zwischen ihnen das Verhältnis, daß in der Gültigkeit des Grundes die der Folge, in der Ungültigkeit der Folge die des Grundes notwendig eingeschlossen ist. Diese logische Tatsache bildet das Fundament der hypothetischen Schlüsse und begründet zugleich ihre Berechtigung. Als logischen Grundsatz der hypothetischen Deduktionen können wir mithin den Satz aufstellen: Mit dem Grunde ist die Folge denknotwendig gesetzt, mit der Folge der Grund denknotwendig aufgehoben.
Nicht so einfach liegen die Dinge bei den kategorischen Deduktionen. Den mannigfachen Theorien des Urteils entsprechen ebenso viele Theorien des syllogistischen Schließens, die kurz skizziert seien:
[S. 92]
Die Auffassungen vom Wesen des syllogistischen Schließens zerfallen (wie beim Urteil) in Umfangs- und Inhaltstheorien. Die Anhänger der Umfangslogik vertreten entweder die Subsumtions- oder Substitutionstheorie des Syllogismus. Nach der Subsumtionstheorie kommt dieser dadurch zustande, daß der Umfang von S in dem von M, der Umfang von M in dem von P und damit der Umfang von S mittelbar in dem von P enthalten gedacht werde (S eine Art der Gattung M, M eine Art der Gattung P; Aristoteles); diese Theorie heißt nach der üblichen Symbolisierung der Umfangsverhältnisse durch Kreise auch „Sphärentheorie“ des Syllogismus. Nach der Substitutionstheorie dagegen, der beim Urteil die Identitätstheorie des Umfangs entspricht, wird der Umfang der drei Begriffe S, M und P nicht untereinander subsumiert, sondern einander substituiert, d. h. als identisch gedacht. Ihr Grundsatz lautet: Gleiches Gleichem substituiert gibt Gleiches; also: S = M, M = P, mithin S = P (Beneke). Diese Deutungen genügen den Erfordernissen der Logik indessen so wenig wie die Umfangstheorien des Urteils. Das gleiche gilt — hier auf den Syllogismus bezogen — auch für die Identitätstheorie des Inhalts, nach der die logische Schlußfolgerung aus der Inhaltsgleichheit von S, M und P hervorgehen müßte.
Der oben entwickelten logischen Theorie des Urteils entspricht eine Einordnungstheorie des Syllogismus. Kommt einem Subjekt das Prädikat M, diesem das Prädikat P zu oder auch nicht zu, dann kommt eben diesem Subjekt mittelbar auch das Prädikat P zu oder nicht zu (S ← M ← P = S (M)← P). Das syllogistische Schließen ist demnach ein Urteilen, und zwar ein mittelbares (d. h. ein durch Urteile vermitteltes) Urteilen. Als Grundsatz der kategorischen Deduktionen können wir mithin schreiben: Jedem Subjekt kommt mittelbar das Prädikat seines Prädikats zu, und keinem Subjekt kommt mittelbar zu, was nicht Prädikat eines Prädikats von ihm ist (Erdmann).
Diese Formulierung gilt aber ersichtlich nur für solche Syllogismen, deren Prämissen fürs erste einfache, zum zweiten Inhärenzurteile sind (Prinzip der mittelbaren Inhärenz). Für die oben sog. Relationssyllogismen und Syllogismen aus hypothetischen Prämissen haben wir mithin den entwickelten Grundsatz noch zu erweitern. Daraus ergeben sich die logischen Grundsätze: Stehen zwei Begriffe zu einem dritten in logischer Relation, so stehen sie mittelbar auch untereinander in einer solchen (Prinzip der mittelbaren Relation); und: Mit dem Grunde ist wie die Folge auch die Folge seiner Folge mittelbar gesetzt; von dem Grunde ist als mittelbare Folge alles ausgeschlossen, was von einer seiner Folgen als Folge ausgeschlossen ist (Prinzip der mittelbaren Folge).
[S. 93]
Prämissen und Konklusio verhalten sich in allen deduktiven Schlüssen wie logischer Grund und Folge. Wie aus der Wahrheit der Prämissen bei formal gültiger Ableitung die Wahrheit des Schlußsatzes, so folgt aus der Falschheit des Schlußsatzes umgekehrt, daß entweder die Ableitung formal ungültig oder aber eine der Prämissen falsch ist. Daß aus falschen Prämissen gelegentlich auch Richtiges folgen kann, beweist gegen diese Tatsachen so wenig, wie der Umstand, daß bei mehreren Fehlern in einer Rechnung gelegentlich Richtiges herauskommt, gegen die Zahlenverhältnisse des kleinen Einmaleins.
Der Wert des deduktiven, speziell des syllogistischen Schließens ist seit dem klassischen Altertum (von Sextus Empiricus bis John Stuart Mill) häufig bezweifelt worden. Eines der schwerwiegendsten Bedenken besagt, daß die Prämissen im Grunde nicht das Schlußurteil begründen, sondern dessen Gültigkeit voraussetzen. In dem beliebten Beispiel: „Alle Menschen sind sterblich, Cicero ist ein Mensch, also ist Cicero sterblich“ sei sowohl die obere wie untere Prämisse nur gültig, wenn die Konklusio Gültigkeit habe. Verneine man diese, so hebe man damit auch die Prämissen auf. Der Schluß erweitere also unsere Erkenntnis nicht, sondern besage nur, was bereits im voraus bekannt ist; sei also wertlos.
Gegenüber solchen und ähnlichen Einwänden tut man gut, auf die Leistungen des deduktiven Schlußverfahrens in den mathematischen sowie den theoretischen Naturwissenschaften hinzuweisen, in denen die Obersätze entweder Definitionen oder Axiome von unmittelbarer Gewißheit oder aber aus solchen abgeleitete mittelbar-gewisse Urteile sind. Vergegenwärtigt man sich, zu welcher Fülle von Einsichten etwa die Geometrie durch syllogistisches Fortschreiten aus wenigen obersten Definitionen und Axiomen gelangt, dann kann von einer Unterschätzung des deduktiven Schließens nicht mehr die Rede sein.
Aber auch in den Tatsachenwissenschaften bilden Deduktionen bedeutsame Mittel der Forschung. Sei es, daß die Ableitung aus einem registrierend allgemeinen Urteil als Obersatz analysierend auf ein darin einbegriffenes Einzelne geht (analysierender Tatsachenschluß), sei es, daß wir aus einem erweiternd allgemeinen Urteil als Obersatz auf ein noch unbekanntes darin einbegriffenes Einzelne schließen und so das induktiv gewonnene Wissen deduktiv ausbeuten (erweiternder Tatsachenschluß): in keiner von beiden Formen ist das deduktive Verfahren als wertloses anzusprechen. Bringt es in dem ersten Falle zwar nur zum Bewußtsein, was in dem registrierend Allgemeinen als Einzelnes enthalten ist, so erweitert es in dem zweiten unsere Erkenntnis sehr wohl, indem es — eine „deduktive Instrumentation unseres induktiven Wissens“ (nach B. Erdmann) — das auf Grund der Erfahrung als allgemeingültig Erkannte auf einen einzelnen dahingehörigen, noch unbekannten Fall überträgt.
Induktive Schlüsse sind solche, in denen aus einer Mehrheit besonderer Urteile ein davon verschiedenes zusammenfassend- oder erweiternd-allgemeines[S. 94] Urteil abgeleitet wird. Sie sind mithin Schlüsse vom Besonderen aufs Allgemeine; ihrer Einteilung nach entweder zusammenfassende oder erweiternde Induktionen.
Das Wesen der zusammenfassenden (auch: registrierenden) Induktionen besteht darin, daß eine beliebig große Anzahl gegebener Urteile mit gleichem Subjekt oder Prädikat im Schlußurteil zu einem Urteil vereinigt wird, wobei die Konklusio in dem einen Fall eine kopulative, im anderen eine konjunktive Urteilsverbindung wird. Demnach können wir ihre Arten als kopulative und konjunktive Zusammenfassungen auseinanderhalten. Als selbständige Schlußweisen haben diese Ableitungen nur untergeordnete Bedeutung, weil ihr Schlußurteil lediglich in formaler Hinsicht von den Prämissen abweicht, dagegen material über den Bestand des in den Prämissen Ausgesagten nicht hinausgeht. Dagegen bilden sie Voraussetzungen der erweiternden Induktionen, als deren logische Vorstufe sie darum bezeichnet werden müssen. — Ihrer — positiven (a) und negativen (b) — Grundform nach lauten sie:
|
I. Kopulative
Zusammenfassungen:
|
||
|
a)
|
b)
|
|
|
S1 ← P
|
S1 ← nicht P
|
|
|
S2 ← P
|
S2 ← nicht P
|
|
|
S3 ← P
|
S3 ← nicht P
|
|
|
. . .
|
. . .
|
|
|
. . .
|
. . .
|
|
|
Sn ← P
|
Sn ← nicht P
|
|
|
[S1, S2, S3,
... und Sn] ← P
|
[S1, S2, S3,
... und Sn] ← nicht P
|
|
|
II. Konjunktive
Zusammenfassungen:
|
||
|
a)
|
b)
|
|
|
S ← P1
|
S ← nicht P1
|
|
|
S ← P2
|
S ← nicht P2
|
|
|
S ← P3
|
S ← nicht P3
|
|
|
. . .
|
. . .
|
|
|
. . .
|
. . .
|
|
|
S ← Pn
|
S ← nicht Pn
|
|
|
S ← [P1, P2, P3,
... und Pn]
|
S ← nicht [P1, P2, P3,
... und Pn]
|
|
Nicht nur formal, sondern auch material von den Prämissen verschieden ist die Konklusio in den sog. erweiternden Induktionen. Diese sind Schlußweisen, in denen aus den gegebenen besonderen[S. 95] Urteilen nicht ein zusammenfassend-, sondern ein erweiternd-allgemeines Urteil abgeleitet wird; und jenachdem ob diese Erweiterung von einigen Arten einer Gattung auf diese Gattung als Ganzes (Umfangserweiterung) oder von einigen Merkmalen eines Begriffes auf dessen Inhalt überhaupt (Inhaltserweiterung) geht, sind sie zweckmäßig teils als verallgemeinernde, teils als ergänzende Erweiterungen zu bezeichnen. Ordnet man die Arten der induktiven Schlüsse nach alledem in einem übersichtlichen Schema, dann ergibt sich folgende Tafel:
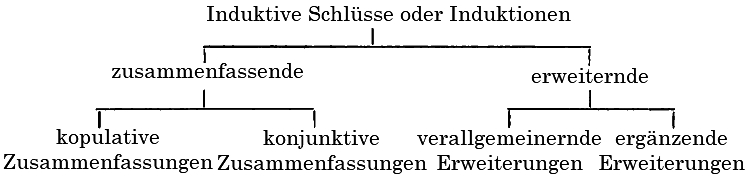
Ihrer einfachsten Form nach — mit einmal bejahenden (a), einmal verneinenden Prämissen (b) — lauten die verallgemeinernden (I) und ergänzenden Erweiterungen (II):
|
I.
|
||
|
a)
|
b)
|
|
|
S1 ← P
|
S1 ← nicht P
|
|
|
S2 ← P
|
S2 ← nicht P
|
|
|
S3 ← P
|
S3 ← nicht P
|
|
|
. . .
|
. . .
|
|
|
. . .
|
. . .
|
|
|
Sn ← P
|
Sn ← nicht P
|
|
|
Alle S ← wahrscheinlich P
|
Kein S ← wahrscheinlich nicht P
|
|
|
II. Konjunktive
Zusammenfassungen:
|
||
|
a)
|
b)
|
|
|
S ← P1
|
S ← nicht P1
|
|
|
S ← P2
|
S ← nicht P2
|
|
|
S ← P3
|
S ← nicht P3
|
|
|
. . .
|
. . .
|
|
|
. . .
|
. . .
|
|
|
S ← Pn
|
S ← nicht Pn
|
|
|
S ← wahrscheinlich
P
|
S ← wahrscheinlich
nicht P
|
|
[S. 96]
Zur Erläuterung seien Beispiele für I a und II a gegeben.
|
I a.
|
II a.
|
|||||||
|
Silber
|
ist
|
ein
|
guter
|
Wärmeleiter
|
Dieser
|
Körper
|
hat eine gelbliche Farbe
|
|
|
Kupfer
|
„
|
„
|
„
|
„
|
„
|
„
|
leuchtet im Dunkeln
|
|
|
Gold
|
„
|
„
|
„
|
„
|
„
|
„
|
ist (z.B. durch Reiben) ungemein leicht entzündlich
|
|
|
Messing
|
„
|
„
|
„
|
„
|
Dieser
|
Körper
|
brent mit helleuchtender Flamme
|
|
|
Zink
|
„
|
„
|
„
|
„
|
Dieser
|
Körper
|
ist in Wasser unlöslich
|
|
|
Zinn
|
„
|
„
|
„
|
„
|
„
|
„
|
schmilzt bei 44,4° C
|
|
|
Eisen
|
„
|
„
|
„
|
„
|
„
|
„
|
siedet bei 290° C unter Bildung farbloser
Dämpfe
|
|
|
Blei
|
„
|
„
|
„
|
„
|
Dieser
|
Körper
|
ist ungemein giftig
|
|
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
...
|
|
|
Alle Metalle werden gute
Wärmeleiter sein.
|
Dieser Körper wird gelber kristallinischer Phosphor
sein.
|
|||||||
Vergleicht man die erweiternden mit den zusammenfassenden Induktionen, so ergibt sich, daß die verallgemeinernde Induktion die kopulative, die ergänzende die konjunktive Zusammenfassung zu ihrer Voraussetzung hat. Der logische Prozeß der Induktion geht vom Einzelnen zunächst zum zusammenfassend-Allgemeinen und von da zur verallgemeinernden oder ergänzenden Erweiterung über. Die Zahl der Prämissen in erweiternden Induktionen kann nie kleiner als zwei, nach oben aber beliebig groß sein. Das Schlußurteil bleibt stets von problematischer (bzw. approximativer) Gültigkeit; denn was für den Teil eines Ganzen als gültig erwiesen ist, gilt für den übrigbleibenden, noch unbekannten Teil desselben Ganzen immer nur mit mehr oder minder großer Wahrscheinlichkeit, nie aber tatsächlich oder notwendig. Die induktiven Schlüsse sind mithin ihrem Wesen nach Wahrscheinlichkeitsschlüsse. Darin liegt ihr charakteristischer Unterschied zu den deduktiven Ableitungen, die im Gegensatz zu ihnen geradezu als Notwendigkeitsschlüsse bezeichnet werden können. Hier wie dort zwar bilden die Prämissen den logischen Grund der Konklusio. Läßt sich der Syllogismus indessen darstellen durch ein hypothetisches Gefüge apodiktischer Konsequenz (wenn S ← M und: wenn M ← P, dann notwendig S ← P), so die Induktion durch ein hypothetisches Gefüge problematischer Konsequenz (wenn S1 ← P, S2 ← P, S3 ← P usw. ..., dann wahrscheinlich alle S ← P). In dem einen ist die Ableitung also denknotwendig, in dem anderen nur wahrscheinlich.
[S. 97]
Die logische Theorie der erweiternden Induktion hat die Frage nach dem Prinzip und aus diesem heraus nach der Berechtigung dieser Schlußarten zu beantworten. Als logische Grundsätze des induktiven Schließens (unter dem jedoch hier nur die Induktion im eigentlichen Sinne, also die erweiternde, nicht deren Vorstufe, die verallgemeinernde, verstanden sei) können wir schreiben: 1. Kommt einer Reihe von Arten gleicher Gattung ein Merkmal als Prädikat zu, dann ist es wahrscheinlich, daß dieses Merkmal allen Arten, mithin der ganzen Gattung, als Prädikat zukommt (Prinzip der verallgemeinernden Induktion); 2. kommt einem Begriff eine Reihe von Merkmalen gleichermaßen als Prädikat zu, dann ist es wahrscheinlich, daß ihm der ganze Inhalt, von dem diese Merkmale einen Teil bilden, als Prädikat zukommt (Prinzip der ergänzenden Induktion). Indem wir versuchen, beide Grundsätze zu einem zusammenzufassen, formulieren wir: Wenn etwas für den Teil eines Ganzen als zutreffend erwiesen ist, dann ist es wahrscheinlich, daß ebendasselbe auch für den übrigbleibenden, noch ununtersuchten Teil dieses Ganzen, mithin für das Ganze überhaupt, Gültigkeit haben werde.
Damit erweist sich der Induktionsschluß deutlich als ein Schluß vom Bekannten aufs Unbekannte. Seine Voraussetzung ist die Hypothese einer durchgehenden kausal-bedingten Gleichartigkeit des Universums. In den nicht bekannten Teilen des Wirklichen werden dieselben Ursachen als gegeben angenommen wie in den bekannten und zugleich dem Schlusse die Annahme zugrunde gelegt, daß aus gleichen Ursachen allemal gleiche Wirkungen hervorgehen (Erdmann). Die Berechtigung des Induktionsschlusses wurzelt also zuletzt in der Berechtigung des Kausalitätsprinzips. Leugnet man, daß alles, was geschieht, zureichende Ursachen hat, durch die es geschieht, und daß aus gleichen Ursachen gleiche Wirkungen hervorgehen, dann leugnet man damit zugleich auch die Berechtigung alles induktiven Schließens; und mit dieser wiederum die Berechtigung aller Erfahrungswissenschaften, die aus dem untersuchten Einzelnen allgemeine Gesetze und Regeln über den Ablauf der Veränderungen im Universum überhaupt herleiten.
Sind die Induktionen Schlüsse vom Besonderen aufs Allgemeine, so bilden ihre Schlußsätze im natürlichen Verlauf des Denkens häufig wiederum Obersätze von deduktiven Ableitungen, die von hier aus abermals zum Besonderen herabsteigen. Diese — an sich leicht und überzeugend einleuchtende — Tatsache hat John Stuart Mill zu dem verhängnisvollen Irrtum verleitet, alle[S. 98] syllogistischen Schlüsse (auch die mathematischen, für die die Voraussetzung eines induktiv gewonnenen Obersatzes nicht einmal zutrifft!) als Schlüsse vom Besonderen aufs Besondere zu deuten, wodurch der Unterschied zwischen Deduktion und Induktion — bei Mill selbst wie seinen Anhängern — bisweilen in bedenklicher Weise verwirrt worden ist. Zur kritischen Beurteilung dieses Standpunktes sind die entscheidenden Gesichtspunkte bereits in dem früher Gesagten angedeutet.
Die induktiven Schlüsse bildeten lange ein Stiefkind der Logiker. Weder Aristoteles noch die Logik des 17. und 18. Jahrhunderts sehen in ihnen eine prinzipiell verschiedene Form gegenüber den Deduktionen. Ihre einseitige Betonung des deduktiven Schließens, die gelegentlich so weit geht, alles Schließen seinem Wesen nach in deduktives zu verwandeln, macht sie zu Vertretern jener Richtung, die wir zweckmäßig als „deduktive Logik“ bezeichnen können (Aristotelische Tradition). Erst das 19. Jahrhundert — vornehmlich John Stuart Mill (der übrigens in David Hume darin einen nicht hoch genug zu würdigenden Vorgänger hat) — weiß von einer Analyse der naturwissenschaftlichen Methoden aus den induktiven Schlüssen mehr und mehr gerecht zu werden. Dabei aber fällt man zugleich in das entgegengesetzte Extrem, indem man unter Verkennung der eigentlichen Bedeutung der Deduktion diese geringschätzig in den Hintergrund stellt oder sogar den Versuch macht, alles Schließen seinem Wesen nach aus dem induktiven abzuleiten. Man nennt diese — besonders in der neueren englischen Philosophie vertretene — Richtung daher die „induktive Logik“. Sachlich soll zu diesem Gegensatz nur bemerkt werden, daß eine den tatsächlichen Verhältnissen des Denkens gerecht werdende logische Analyse weder einen einseitig deduktiven noch einen einseitig induktiven Standpunkt vertreten könne. Deduktion und Induktion bilden ihrem Wesen nach charakteristisch verschiedene, ihrem Wert nach gleich bedeutungsvolle Formen des Denkens, deren höchste Vollendung erst in ihrem — in den neueren Naturwissenschaften in klassischer Form vollzogenen — Zusammenwirken gegeben ist. Das System der Logik darf also kein deduktives und kein induktives — es muß vielmehr ein deduktiv-induktives zugleich sein.
Von den Deduktionen — als Schlüssen vom Allgemeinen aufs Besondere —, den Induktionen — als Schlüssen vom Besonderen aufs Allgemeine — scheidet die logische Tradition die Schlüsse vom[S. 99] Besonderen aufs Besondere, die sie als Schlüsse per analogiam oder kurz als Analogieschlüsse (Ähnlichkeitsschlüsse) bezeichnet. Diese sind, wie sich zeigen wird, als Wahrscheinlichkeitsschlüsse ihrem Prinzip nach den Induktionsschlüssen verwandt, nichtsdestoweniger als besondere Art der mittelbaren Schlüsse zu betrachten. Ihre Form lautet:
|
M ← P
|
|
S ← M ähnlich
|
|
S ← wahrscheinlich P
|
|
An Beispielen:
|
||
|
Die Erde ist von lebenden Wesen bewohnt.
|
|
Die Menschen sind beseelt.
|
|
Der Mars ist der Erde ähnlich.
|
Die Wirbeltiere sind den Menschen ähnlich.
|
|
|
Mars ist wahrscheinlich von lebenden Wesen bewohnt.
|
Die Wirbeltiere sind wahrscheinlich beseelt.
|
|
Die Analogieschlüsse sind mittelbare Schlüsse, da in ihnen das Schlußurteil aus einer Mehrheit gegebener Prämissen abgeleitet wird; sie sind erweiternde Schlüsse, insofern das Schlußurteil über den materialen Bestand der Prämissen hinausgeht; sie sind endlich Schlüsse vom Besonderen aufs Besondere, insofern aus besonderen Prämissen ein besonderes Schlußurteil gewonnen wird. Ihre Konklusio ist stets von problematischer (bzw. approximativer) Gültigkeit; denn aus der Ähnlichkeit zweier Objekte kann nie assertorisch oder apodiktisch, stets nur möglich oder wahrscheinlich geschlossen werden.
Die Analyse der Schlüsse per analogiam führt auf das logische Problem der Ähnlichkeit. Ähnlich nennen wir zwei Gegenstände, wenn sie in ihrer begrifflichen Bestimmung ein oder mehrere wesentliche Merkmale miteinander gemeinsam haben, in anderen wesentlichen oder unwesentlichen Merkmalen aber voneinander abweichen. Die Ähnlichkeit hat dabei einen um so höheren Grad, je mehr Merkmale gleich, je weniger verschieden sind. Der Analogieschluß geht nun den Weg, daß er aus der Ähnlichkeit von S und M das Schlußurteil ableitet, daß ein M zukommendes Prädikat wahrscheinlich auch S zukommen werde; und der Grad dieser Wahrscheinlichkeit ist im allgemeinen um so höher, je größer die Ähnlichkeit ist. Das Prinzip dieser Schlußformen ist also: Kommt einem Begriff ein Merkmal zu, der mit einem anderen Begriffe wesentliche Merkmale gemeinsam hat, so ist es wahrscheinlich, daß ebendieses Merkmal auch jenem anderen[S. 100] Begriffe zukommt. Die Analyse dieses Prozesses führt etwa auf folgenden Gedankengang: In M sind gewisse Ursachen gegeben, aus denen das P-sein als Prädikat folgt; S hat mit M wesentliche Merkmale gemeinsam; also werden auch in S gewisse Ursachen für ein P-sein gegeben sein; also wird S auch P sein. Aus dieser Aufstellung wird ersichtlich, wie nahe verwandt die Ähnlichkeitsschlüsse den induktiven sind, aber auch in welcher Hinsicht sie von ihnen charakteristisch abweichen. Die Analogieschlüsse sind Wahrscheinlichkeitsschlüsse geradeso wie die induktiven; wie diese setzen auch sie die Gültigkeit des Kausalprinzips in dem oben erörterten Sinne voraus. Ist aber das Denkverfahren bei jenen ein Schluß vom Bekannten aufs Unbekannte und von da aus aufs Allgemeine (Bekannte wie Unbekannte zugleich), so hier ein Schluß vom gegebenen Bekannten auf ein unzureichend, aber dem Gegebenen als ähnlich Bekanntes, ein Schluß also, der vom Besonderen ausgehend beim Besonderen stehen bleibt. Insofern nun in allen Induktionen dem Schluß vom Besonderen aufs Allgemeine ein Schluß vom Besonderen aufs Besondere immanent ist, kann man sagen, daß das Verfahren der Analogieschlüsse seinem Wesen nach bereits in dem Verfahren der Induktion enthalten sei. Das darf aber nicht dazu führen, Induktions- und Analogieschluß — wenn sie auch nahe verwandte Formen des Schließens sind — als unterschiedslos ansprechen oder gar diesen aus jenem ableiten zu wollen. Schon daß der eine beim Besonderen halt macht, während für den anderen der Schluß vom Besonderen aufs Besondere nur der Durchgangspunkt für die Ableitung des Allgemeinen ist, begründet genügend ihre Verschiedenheit. Der eine ist ferner ein Schluß vom Bekannten aufs Ähnliche, der andere vom Bekannten aufs Gleichartige. Und: wohl ist alles Gleichartige ähnlich, aber nicht alles Ähnliche auch gleichartig!
Nicht schwer ist es, zu erkennen, daß das Verfahren der Schlüsse per analogiam, geradeso wie das induktive, von dem deduktiven, speziell dem syllogistischen, wesensverschieden ist. Das ist darum wichtig zu betonen, weil die Form der Ähnlichkeitsschlüsse leicht den Schein erwecken könnte, daß es sich hier um eine Art der sog. Relationssyllogismen handelt. Stellen wir beide Formen nebeneinander, dann ergibt sich:
| I. |
M ← ähnlich P
|
|
Relationssyllogismus
aus Ähnlichkeitsbeziehung. |
|
S ← ähnlich M
|
|||
|
S ← ähnlich P
|
| II. |
M ← P
|
|
Analogieschluß.
|
|
S ← ähnlich M
|
|||
|
S ← wahrscheinlich P
|
[S. 101]
Eine Vergleichung beider Schlußformen zeigt deutlich ihre Verschiedenheit. Relationssyllogismen sind solche, bei denen 1. aus Relationsurteilen als Prämissen ein Relationsurteil als Konklusio folgt, und bei denen 2. die Modalität der Prämissen im Schlußurteil erhalten bleibt. Beide Bedingungen treffen aber für die Analogieschlüsse nicht zu. Also sind Analogieschlüsse keine Relationssyllogismen. Ebensowenig sind sie nun syllogistische Formen überhaupt. Wäre das der Fall, dann müßte sich aus den Grundsätzen des syllogistischen Schließens ein Prinzip ableiten lassen, das für Analogieschlüsse Gültigkeit hat und etwa lautete: Einem Subjekt kommt wahrscheinlich als Prädikat zu, was einem mit ihm als ähnlich erkannten Subjekt als Prädikat zukommt. Dieses Prinzip aber läßt sich aus keinem der angeführten Grundsätze syllogistischer Schlußweisen ableiten. Mithin sind Analogieschlüsse keine Syllogismen[15].
Den Analogieschlüssen kommt sowohl im praktischen wie im wissenschaftlichen Denken eine hohe Bedeutung zu. Wo wir die Ausdrucksbewegungen eines Tieres oder Menschen als durch Schmerz, Freude, Trauer, Mitleid, Haß usw. bewirkt deuten, da bewegen wir uns auf dem Gebiete der Analogien. Alle wissenschaftliche Psychologie, die über das in der Selbstwahrnehmung Gegebene hinausgeht, beruht auf Schlüssen per analogiam. Analogieschlüsse bilden demnach das wesentliche methodische Fundament der Kinderpsychologie und die ausschließliche Grundlage der Psychologie der Tiere, der wilden Völker, der geistig-Minderwertigen oder -Gestörten (Psychopathologie). Als mittelbare methodische Voraussetzungen spielen sie ferner in der Geschichtswissenschaft und der Völkerkunde eine Rolle, insofern als wir in diesen überall stillschweigend voraussetzen, daß die Menschen früherer Zeiten in ebender Weise gedacht und gefühlt haben wie wir selbst, nicht qualitativ, sondern höchstens graduell von uns verschieden. Damit ist die hohe Bedeutung der Ähnlichkeitsschlüsse trotz des relativ geringen Grades ihrer Gültigkeit prinzipiell erwiesen und ihnen unter den Arten der mittelbaren Schlüsse die Stellung zugewiesen, die ihnen ihrem Wesen und ihrer Leistung nach gebührt.
[11] Dafür im folgenden meistens die Abkürzungen: „Grdurt.“ und „Flgsurt.“
[12] Lediglich aus Zweckmäßigkeitsgründen der Darstellung werden im folgenden allgemeines und generelles, modal-bestimmendes und elementares, verneinendes und bejahendes Urteil wie einander koordinierte Urteilsformen behandelt.
[13] „Quidquid de omnibus valet, valet et de quibusdam et singulis: quidquid de nullo valet, nec de quibusdam vel singulis valet.“ (Was allgemein gilt, gilt auch für das Besondere und Einzelne; was für nichts gilt, gilt auch nicht für das Besondere und Einzelne.)
[14] Aristoteles freilich versteht unter „Syllogismus“ zugleich auch die induktiven und Analogieschlüsse, die er irrtümlich aus dem deduktiven Verfahren ableitet. Hypothetische und disjunktive Deduktionen im Unterschied zu den kategorischen kennt er überhaupt noch nicht.
[15] Der Schüler stelle übungshalber fest, nach welchen Schlußformen in diesem Absatz geschlossen worden ist.
[S. 102]
Historisch betrachtet ist das unwissenschaftliche oder praktisch gerichtete Denken des gemeinen Volkes älter als das wissenschaftliche und zugleich der Mutterboden, auf dem jenes unter allmählichen charakteristischen Veränderungen sich entwickelt hat. Die Formen, in denen beide sich vollziehen, sind dieselben: hier wie dort Urteile über Gegenstände, die zuvor durch andere Urteile begrifflich fixiert sind, und Schlüsse, die aus gegebenen Urteilen neue gewinnen lassen. Ziel und Mittel beider sind dagegen wesentlich verschieden. Dient das unwissenschaftliche Denken vorwiegend praktischen Zwecken der Lebensführung, so das wissenschaftliche — seinen unmittelbaren Aufgaben nach — theoretischen der Erkenntnis. Jenes ist einseitig, subjektiv-individuell und dem Augenblick angehörend, dieses umfassend, objektiv-allgemein und dem Ideal nach für die Ewigkeit bestimmt. Und dem Zweck entsprechen die Mittel: unwissenschaftliches Denken ist unkritisch und unsystematisch, allen Verführungen des Hoffens, Meinens und Glaubens willfährig hingegeben; wissenschaftliches dagegen eine kritisch-systematische Reflexion des Bewußtseins auf seine Gegenstände, in der an die Stelle des Hoffens das Forschen, an die Stelle des Meinens das Beweisen, an die Stelle des Glaubens das Wissen tritt. Wissenschaftliches Denken ist also kurz gesagt solches, das seinen Gegenständen nach einen möglichst vollständigen, seinem Erkenntniswert nach einen möglichst allgemeingültigen Bestand von Urteilen über das Wirkliche erstrebt. Zu diesem Zwecke hat es zwei miteinander eng zusammenhängende Aufgaben zu erfüllen: 1. seine Gegenstände systematisch zu untersuchen; 2. die Ergebnisse dieser Untersuchung in ihrem Zusammenhange zureichend zu begründen. Entsprechend diesen beiden Aufgaben zerfällt die logische Methodenlehre — als wissenschaftliche Reflexion auf die methodischen Formen des wissenschaftlichen Denkens — in zwei Hauptteile, deren ersten die Lehre[S. 103] vom wissenschaftlichen Untersuchungs-, deren zweiten die Lehre vom wissenschaftlichen Beweisverfahren bildet. Nicht selten wird zu diesen beiden Teilen noch ein dritter hinzugesellt: die Lehre von der systematischen Darstellung wissenschaftlicher Ergebnisse. Dieser ist jedoch — soweit er logisch- (und nicht praktisch-didaktisch-) Wertvolles enthält — bereits völlig in den beiden anderen Teilen der Methodenlehre enthalten; denn jede wissenschaftliche Untersuchung, die zu Ergebnissen gelangt, muß, um diese festzuhalten, zu deren systematischer Darstellung fortschreiten, und jeder Versuch, wissenschaftliche Ergebnisse in ihrem Zusammenhange zureichend zu begründen, muß von einer systematischen Darstellung dieser Ergebnisse seinen Ausgangspunkt nehmen.
Die Aufgaben der logischen Methodenlehre werden dadurch verwickelter, daß das wissenschaftliche Denken seiner Form nach nicht ein einheitliches, sondern vielmehr ein in vielen Richtungen auseinanderstrebendes Ganze bildet. Mit der Differenzierung der Wissenschaften haben sich auch ihre methodischen Formen zu immer feineren voneinander abweichenden Gestaltungen entwickelt. Das wissenschaftliche Denken ist also wie nach seinen Gegenständen so auch nach seinen Methoden charakteristisch verschieden, und es fragt sich, wie die logische Methodenlehre sich diesen methodischen Verzweigungen gegenüber zu verhalten habe.
Während die älteren Logiker sich darauf beschränkten, lediglich die allgemeinen Grundlagen des wissenschaftlichen Untersuchungs- und Beweisverfahrens festzulegen, haben sich in der jüngeren Logik — namentlich durch den (trotz aller Schwächen im einzelnen) epochemachenden Entwurf Wundts — Ansätze entwickelt, die von der allgemeinen auf eine spezielle Methodenlehre des einzelwissenschaftlichen Denkens hinstreben. In diesen Versuchen zeigt sich die Tendenz, wie eine Logik des mathematischen so auch eine solche des naturwissenschaftlichen und davon wieder unterschieden eine solche des geisteswissenschaftlichen (bsd. des historischen) Denkens zu begründen. Diese — z. B. von Windelband, von Rickert angeregten und geförderten — Bestrebungen sind indessen noch zu jung, um bereits anerkannte Ergebnisse von bleibender Bedeutung aufzuweisen. Für künftige Logiker jedoch — gleich gut geschult auf einzelwissenschaftlichem wie philosophischem Gebiete — eröffnen sich hier weite, noch ungepflügte Gebiete der Forschung, die reichen Ertrag versprechen.
[S. 104]
Gegenwärtig und im besonderen für den vorliegenden Zweck muß die Darstellung der logischen Methodenlehre sich auf die Skizzierung der allgemeinsten methodischen Grundlagen des wissenschaftlichen Denkens beschränken, nur daß sie gut tut, gegebenen Ortes auch der wichtigsten Differenzierungen kurz Erwähnung zu tun.
Das wissenschaftliche Denken zerfällt nach seinen Gegenständen in so viel Arten, wie man Arten der Wissenschaften nach ihren Untersuchungsgebieten unterscheidet. Zufolge der überlieferten — in der Gegenwart zum Teil heftig angegriffenen — Klassifikation der wissenschaftlichen Disziplinen zerfallen diese in Formal- und Realwissenschaften. Die Formalwissenschaften sind der Inbegriff der mathematischen Wissenschaften; sie zerfallen in die beiden Hauptarten der Geometrie und Arithmetik. Die Realwissenschaften sind der Inbegriff der Tatsachenwissenschaften; sie zerfallen nach der herkömmlichen Scheidung in die beiden Hauptarten der Natur- und Geisteswissenschaften. Die Naturwissenschaften sind wieder entweder systematische (Gesetzes-) oder genetische (Entwicklungs-) Wissenschaften; die systematischen entweder: beschreibende und erklärende oder: beschreibende und klassifizierende. Zu den ersteren gehören Physik, Chemie, Astronomie und Physiologie; zu den letzteren Zoologie, Botanik, Mineralogie, wohl auch Ethnologie und Anthropologie, Geographie, Anatomie und vergleichende Morphologie. Die genetischen Naturwissenschaften dagegen sind die Wissenschaften von dem Entwicklungszusammenhang der Natur, also Kosmologie, Geologie, genetische Biologie (Entwicklungslehre). — Schwankender als diese ist die Einteilung der Geisteswissenschaften. Diese sind, sofern sich in ihnen die Untersuchung unmittelbar auf das Geistige als solches richtet, psychologische, sofern sie das Geistige in dem durch Menschenhand Geschaffenen, also mittelbar, zum Gegenstand hat, Kulturwissenschaften. Auch hier wiederum zeigt sich bei beiden der Unterschied zwischen den systematisch- und genetisch-gerichteten Disziplinen. Systematisch-psychologische Forschungszweige sind die allgemeine Psychologie des normalen Bewußtseins, die Charakterpsychologie oder Psychologie der individuellen Differenzen, die Rassen- und Völker- sowie die Tier-, die Kinder- und die noch unbegründete Greisenpsychologie (die die charakteristisch seelischen Veränderungen des zunehmenden Alters zum Gegenstand hat); genetisch-psychologische dagegen die biologische Psychologie, die die Entwicklung des[S. 105] Seelischen überhaupt, sowie die ethnologische und biographische Psychologie, die die seelische Entwicklung entweder bestimmter Völker oder bestimmter Individuen zum Gegenstand haben. Systematische Kulturwissenschaften endlich sind Wissenschaften wie die allgemeine und vergleichende Staats-, Rechts- und Wirtschaftswissenschaft, Literatur- und Sprach-, Kunst- und Moral-, Religionswissenschaft und Pädagogik; genetische Kulturwissenschaften alle historischen Disziplinen, als da sind: politische und Kulturgeschichte, Sprach- und Literatur-, Kunst- und Religionsgeschichte sowie die Geschichte der Philosophie und der Wissenschaften selbst.
Für die Anordnung der Wissenschaften nach methodischem Gesichtspunkte gibt einmal die Einteilung der Urteile in Formal- und Realbehauptungen, zum anderen die durchgehende Scheidung der Tatsachenwissenschaften nach systematischem und genetischem Gesichtspunkte genügenden Anhalt. Die mathematischen Wissenschaften sind entsprechend alt-überlieferten Annahmen ihrer Methode nach wesentlich rational-deduktive, die Tatsachenwissenschaften empirisch-induktive. Alle empirisch-induktiven Wissenschaften wiederum sind ihrer Methode nach entweder systematische oder genetische, d. h. entweder gesetzbildende oder Entwicklungswissenschaften (in Windelbandscher Terminologie: nomothetische oder idiologische Disziplinen). Diese Scheidung ist indessen nur eine Typeneinteilung, d. h. eine solche, zwischen deren Einteilungsgliedern fließende Grenzen bestehen; denn es muß anerkannt werden, daß es sowohl in gewissen Entwicklungswissenschaften Gesetze wie in gewissen Gesetzeswissenschaften untersuchte Entwicklungszusammenhänge gibt (ein Faktum, für dessen Begründung im einzelnen hier nicht der Ort ist).
Das wissenschaftliche Denken baut nicht überall von Anfang an auf eigenem Grunde. Es findet, indem es an die Untersuchung seiner Gegenstände herantritt, in den Begriffen, in denen diese gemeinhin gedacht werden, einen Bestand von Urteilen vor, die, dem unwissenschaftlichen (oder vorwissenschaftlichen) Denken entstammend, nicht unbesehen in das wissenschaftliche einfließen dürfen. Hier ergibt sich für den Forscher die Aufgabe, die Begriffe, die er aus dem praktischen[S. 106] Denken übernimmt, einer wissenschaftlichen Kritik zu unterziehen und sie damit zu wissenschaftlichen zu erheben.
Alle wissenschaftliche Begriffsbildung geht von einer planmäßig-geordneten Untersuchung derjenigen Gegenstände aus, die zu dem in Betracht kommenden Forschungsgebiet gehören. Die Gegenstände der Forschung sind nicht alle solche der Wahrnehmung; vielmehr haben wir neben diesen auch andere anzuerkennen, die das Denken auf Grund der Inhalte der Wahrnehmung selbsttätig bildet. Dahin gehören z. B. die Gegenstände der mathematischen Wissenschaften. Ein Dreieck, ein Kreis, eine Zahl sind niemals Objekte der Wahrnehmung, sondern immer Produkte des Denkens. Man kann sich diese wohl durch eine äußerlich wahrnehmbare Zeichnung versinnbildlichen: die Zeichnung aber ist stets nur das Abbild des Dreiecks, des Kreises, nie diese selbst. Hieraus erklärt sich die Klarheit und Stetigkeit der mathematischen Begriffe. Um den Begriff des Dreiecks, des Kreises zu bilden, braucht man nicht alle die verschiedenen Arten möglicher Dreiecke, möglicher Kreise einzeln durchzugehen. Die logische Reflexion auf das Wesen eines einzigen von ihnen ergibt vielmehr die Wesensbestimmung aller. Darum bleibt der Begriff des Dreiecks, des Kreises, einmal gebildet, immer derselbe. Erfahrungsbegriffe können sich wandeln: Verstandesbegriffe bleiben konstant.
Die Gegenstände der Tatsachenwissenschaften sind zwar in der Wahrnehmung, aber nicht alle in gleicher Weise in dieser gegeben. Bilden die Objekte der systematischen Wissenschaften unmittelbare, so die der genetischen nur mittelbare Gegenstände der Wahrnehmung. Die Sauerstoffverbindung, die elektrische Strahlenart, die besondere Tier- oder Pflanzenspezies, die ich untersuche, sind mir in der sinnlichen, die Tonempfindung, das Unlustgefühl des Zornes in der Selbstwahrnehmung unmittelbar präsent[16]. Die Beschaffenheit der Erdoberfläche in der Eiszeit dagegen, die kulturellen Verhältnisse in Europa zur Zeit Heinrichs IV., die Faktoren, die den Ausbruch des Siebenjährigen Krieges herbeiführten, sind mir nicht unmittelbar gegeben, sondern müssen als nach Analogie der unmittelbaren Wahrnehmungsobjekte[S. 107] gedachte Gegenstände aus den Resten und Zeugnissen dieser Perioden von mir erschlossen werden. Hier tritt als methodischer Faktor an die Stelle der Wahrnehmung und der auf ihr beruhenden Erinnerung die wissenschaftlich-geleitete Einbildungskraft (vgl. B. Erdmann, Die Funktionen der Phantasie im wissenschaftlichen Denken, Berlin 1913).
Alle Begriffsbildung geschieht durch Urteile; die wissenschaftliche mithin durch wissenschaftliche Urteile. Wissenschaftliche Begriffe sind also nicht Voraussetzungen, sondern vielmehr Produkte wissenschaftlicher Arbeit. Sie wandeln sich — abgesehen von der den Grundbegriffen der Mathematik eigenen Konstanz — in und mit dem Fortschreiten der Forschung, indem die spezielleren Begriffsformen an Zahl immer zunehmen, an Inhalt dabei reicher, an Umfang ärmer werden, während sich darüber ein wachsendes, immer verwickelter sich gestaltendes System von Art- und Gattungsbegriffen aufbaut. In den systematischen und genetischen Disziplinen ist der Vorgang der Begriffsbildung dabei nicht wesentlich voneinander verschieden: die ersten gehen — um es nur in allgemeinster Form anzudeuten — von Individuen zu Arten und Gattungen, suchen also das Allgemeine aus dem Einzelnen zu gewinnen; die anderen gehen von Spezialbegriffen zu Gesamtbegriffen, suchen also das Allgemeine im Einzelnen. Aus diesen im Prinzip übereinstimmenden Verfahrungsweisen ergibt sich zugleich die spezifische Differenz beider: die systematische Forschung untersucht das Einzelne um des Allgemeinen willen; sie strebt nach dem Gesetz der Veränderung, also nach dem Sein im Werden, dem „Immer-so-Seienden“; die genetische Forschung dagegen untersucht das Einzelne um seiner selbst willen; sie strebt nach der Feststellung der Entwicklung selber, also nicht nach dem Sein im Werden, sondern nach dem Werden an und für sich selbst, nach dem „Einmal-so-Gewesenen“.
Wissenschaftliche Begriffe sind logisch eindeutig bestimmt, wenn ihnen durch die Spezifikation ihres Inhalts im Gesamtsystem der Wissenschaft ein logischer Ort zugewiesen ist, durch den ihr Umfang deutlich hervortritt. Die Bestimmung eines wissenschaftlichen Begriffes oder seine Definition geschieht, wie bereits früher erwähnt, auf die Weise, daß durch Angabe der nächsthöheren Gattung (Klassifikation) der logische Ort und der Umfang, durch Angabe der wesentlichen Merkmale, zufolge deren er sich von anderen Arten derselben Gattung[S. 108] unterscheidet (diese heißen artbildende Unterschiede [differentiae specificae], das ganze Verfahren Spezifikation), sein notwendiger Inhalt festgelegt ist. Die Definition besteht also in einer konjunktiven Urteilsverbindung, deren Subjekt den zu definierenden Begriff (definiendum), deren Prädikat die Angabe der nächsthöheren Gattung und die der artbildenden Unterschiede enthält. (Eine alte Schulregel besagt: „Definitio fit per genus proximum et per differentiam specificam“[17].) Beispiele dafür sind: „Ein ebenes Dreieck ist eine Fläche, die von drei geraden Linien begrenzt ist; eine Kalorie ist diejenige Wärmemenge, die erforderlich ist, um die Temperatur eines Gramm Wassers von 15° auf 16° Celsius zu erhöhen.“
Aus dieser Regel folgt, daß solche Begriffe undefinierbar sind, denen keine höhere Gattung mehr zukommt (z. B. der Begriff des Seins oder des Etwas überhaupt als der höchsten Gattung gegenüber den Kategorien und allen anderen Begriffen). Individualbegriffe sind dagegen wohl definierbar; denn Individuen sind allemal Arten einer Gattung, als solche von den ihnen nebengeordneten Arten spezifisch verschieden (z. B.: „Faust war ein Mensch, der in der ersten Hälfte des 16. Jahrhunderts lebend als umherziehender Zauberkünstler Aufsehen erregte, so daß sich Sage und Dichtung seiner Gestalt bemächtigte“).
Jede Definition oder Begriffsbestimmung setzt als Urteil die Kenntnis und eindeutige Bestimmtheit anderer Begriffe voraus, die Definition des Begriffes „Dreieck“ z. B. die Kenntnis der Begriffe: Fläche, drei, gerade Linie und begrenzen. Das ist eine der Natur der Sache nach nicht zu vermeidende Unvollkommenheit des Denkens. Wollte man alle Begriffe, durch die man definiert, wiederum definieren, so würde das ein ins Unendliche gehender Prozeß werden. Als praktische Forderung aber darf gelten, nur solche Begriffe als bekannt vorauszusetzen, die in der Tat eindeutig bestimmt Allgemeingut des Denkens geworden sind.
Als häufigste Fehler des Definierens pflegt die traditionelle Logik vier aufzuzählen. Eine Definition ist formal unzulänglich, wenn sie 1. einen Zirkel beschreibt, d. h. wenn sie den zu definierenden Begriff in der Definition selbst als bekannt voraussetzt (idem per idem[S. 109] definit; Diallele); 2. wenn sie abundant ist, d. h. außer den wesentlichen auch daraus abgeleitete unwesentliche Merkmale angibt, wodurch sie zur aufzählenden Beschreibung wird (abundatio notarum); 3. wenn sie zu weit oder zu eng ist, d. h. wenn sie wesentliche Merkmale zuwenig oder zuviel angibt, wodurch der Inhalt entweder zu arm oder zu reich, der Umfang zu reich oder zu arm wird; und endlich 4. wenn sie eine Negation bildet, d. h. wenn sie lediglich die Zugehörigkeit von Merkmalen zu dem Inhalt ihres Subjekts aufhebt und dadurch zwar angibt, was der Gegenstand der Definition seinem Wesen nach nicht ist, aber nicht, was er ist.
Die traditionelle Logik kennt außer der hier entwickelten Form der Begriffsbestimmung noch andere Arten. Einer alten, längst überholten Überlieferung gehört die Einteilung in Nominal- und Realdefinitionen an. Nominaldefinitionen oder Namenerklärungen (z. B. „Psychosen sind Geistesstörungen; herpes tonsurans heißt Bartflechte“) sind keine Definitionen, weil sie sich auf die Bedeutung von Worten, nicht aber auf die Inhaltsbestimmung von Begriffen beziehen. — Als Arten der Realdefinitionen unterscheidet die Überlieferung ferner systematische (das sind die hier besprochenen) und genetische Definitionen, die letzteren als solche, die im Prädikat eine erschöpfende Bestimmung über den Ursprung des zu definierenden Gegenstandes enthalten (z. B. „Ein Kreis entsteht, wenn man alle Punkte, die von einem gegebenen Punkte gleichen Abstand haben, durch eine Linie verbindet“). Auch die genetischen Definitionen sind indessen nicht als wissenschaftliche Begriffsbestimmungen in dem geforderten Sinne zu bezeichnen; denn sie besagen weder etwas über den logischen Ort und Umfang noch Ausreichendes über den notwendigen Inhalt des zu definierenden Begriffes.
Das wichtigste methodische Mittel wissenschaftlicher Forschung ist die Analyse der Untersuchungsobjekte. Einen Gegenstand analysieren heißt: ihn in seine Komponenten zerlegen, ihn auflösen und zergliedern. So zerlegt die psychologische Analyse einen Wahrnehmungsinhalt in seine einfachen Empfindungsbestandteile; die anatomische einen tierischen Körper in Organe, diese in Gewebe und die Gewebe wiederum in Zellen; die historische einen Zeitabschnitt in die einzelnen Vorgänge, die die Gesamtentwicklung herbeiführen. Die letzten Teilinhalte, die sich durch Analyse ergeben, nennen wir Elemente und verstehen darunter die einfachen, d. h. nicht mehr zerlegbaren Faktoren, in die sich ein zusammengesetzter Gegenstand auflösen läßt. Der Begriff des Elementes als des einfachen Teiles eines Ganzen ist dabei relativ. Zu allen Zeiten hat man gewisse Produkte der[S. 110] analytischen Forschung für einfach gehalten, die sich im weiteren Fortgang der Erkenntnis wiederum als zusammengesetzt, ja bisweilen sogar als kompliziert aufgebaute Mischungen oder Verbindungen von Teilinhalten erwiesen haben. Als Beispiel dafür mag die Chemie gelten. Zur Zeit des Aristoteles etwa kennt man nur vier Elemente, und zwar das Feuer und die Erde als das Warme und Kalte, das Wasser und die Luft als das Feuchte und Trockene; heute zählt man in der modernen Chemie bereits etwa 80 Elemente — und man darf fragen: wieviel wird man in abermals 2000 Jahren zählen?
Das analytische Untersuchungsverfahren setzt psychologisch die Anstellung aufmerksamer, d. h. zur Beobachtung gesteigerter Wahrnehmungen voraus und, insofern diese wissenschaftlichen Zwecken dienen, die Anstellung wissenschaftlich-geleiteter, d. h. methodisch-fortschreitender Beobachtungen. Die analysierende Beobachtung hat ihren Gegenstand — teils mit, teils ohne technische Hilfsmittel — in seine Teilkomponenten zu zerlegen, d. h. in ihm das Einzelne gegenüber dem Ganzen zu unterscheiden, dieses miteinander zu vergleichen und in Beziehung zu setzen. Daraus ergeben sich durch Aufzählung der Reihe nach die Merkmale, die jenen Gegenstand kennzeichnen. Die Analyse führt also zur Beschreibung ihres Untersuchungsobjektes, indem sie dessen — wesentliche und unwesentliche — Merkmale, wie sie sich ihr ergeben, unterschiedslos festlegt.
Als Arten des analytischen Verfahrens unterscheidet man eine innere und äußere, eine qualitative und quantitative, eine genetische und systematische Analyse. Die innere (oder immanente) Analyse ist diejenige, die ihren Gegenstand in sich selbst zerlegt; sie führt zu Inhärenzurteilen, besonders zu deren erstbesprochener Art, den Qualitätsurteilen; die äußere (oder Beziehungs-) Analyse ist diejenige, die ihren Gegenstand nicht in sich selbst untersucht, sondern ihn mit anderen vergleicht und daraus Beziehungsmerkmale gewinnt; sie führt zu Relationsurteilen. Qualitativ ist die analytische Forschung — sei sie immanent oder relativ —, wenn sie nur auf das wie beschaffen ihrer Objekte; quantitativ, wenn sie auch auf das wie viel und wie groß eingeht. Danach setzt die quantitative Analyse die qualitative voraus oder kann zum mindesten nicht ohne jene vor sich gehen. Systematisch endlich nennen wir eine Analyse — sei sie immanent oder relativ, qualitativ oder quantitativ —, die ihr Untersuchungsobjekt nach seinem gegenwärtigen Bestande in die[S. 111] Elemente zerlegt; genetisch diejenige, die ihren Gegenstand auf Ursprung und Entwicklung (also das nicht-mehr-Gegenwärtige rekonstruierend) untersucht.
Überall, wo wir im analysierenden Verfahren zählen oder messen, also mathematische Einheiten anwenden (angewandte Mathematik), bewegen wir uns auf dem Boden der quantitativen Analyse. Das Pythagoreische Wort, daß die Welt aus Zahlen bestehe, bedeutet im Grunde nichts anderes: als daß sie einer exakten Maßbestimmung zugänglich sei. Astronomie, Physik und Chemie danken zum großen Teil ihre bewunderungswürdige Exaktheit der Tatsache, daß sie sich mathematischer Hilfsmittel bedienen; man nennt sie daher auch mathematische Naturwissenschaften oder exakte Wissenschaften. Es ist eine Überschätzung, aber eine solche, deren Beweggrund man verstehen kann, wenn Kant gelegentlich gemeint hat, in aller Erkenntnis werde nur so viel eigentliche Wissenschaft angetroffen, als Mathematik darinnen sei.
Quantitative Analysen finden sich auch in den Geisteswissenschaften. Man hat — seit Weber, Fechner und Wundt — mit gutem Glück den Versuch gemacht, auch die seelischen Erscheinungen einer quantitativen Bestimmung zugänglich und damit die Psychologie zur exakten Wissenschaft zu machen. Eine besondere Bedeutung kommt hierbei dem — auch in den systematischen Staatswissenschaften überaus ergebnisreich angewandten — statistischen Verfahren zu. Die Statistik ist ein wissenschaftliches Forschungsmittel, durch das komplexe Erscheinungen des politischen, wirtschaftlichen und seelischen Lebens quantitativer Bestimmung unterzogen werden. Ein englischer Arzt, William Petty, hat sie wegen ihrer eminenten Bedeutung in den Staatswissenschaften „politische Arithmetik“ genannt. Neuerdings aber hat sie sich auch durch ihre nutzbringende Aufnahme in differential- und völkerpsychologische, ästhetische und pädagogische Untersuchungen zu einer Art „Arithmetik seelischer Erscheinungen“ ausgebildet.
Wo der Forscher die Bedingungen, unter denen sein Untersuchungsobjekt steht, willkürlich und nach vorgefaßtem Plan verändert, da bedient er sich des Experiments. Dieses ist eines der wichtigsten[S. 112] methodischen Hilfsmittel des analytischen Verfahrens; ihm allein dankt die moderne Wissenschaft eine unendliche Zahl ihrer wertvollsten Ergebnisse.
Die Geschichte des experimentellen Verfahrens in der neueren wissenschaftlichen Forschung ist bisher nicht geschrieben. Seine Erfindung verdanken wir wahrscheinlich dem Zufall. Wer mit dem Spieltrieb des Kindes zum erstenmal Wachs erwärmt hat, um zu sehen, was daraus wird, oder ein Tier geschlagen, um zu sehen, wie es reagiert, der kann als Erfinder des Experiments angesehen werden. Als methodisches Werkzeug wissenschaftlicher Forschung freilich beginnt es erst seit dem 18. Jahrhundert eine bedeutungsvolle Rolle einzunehmen. In dieser Zeit entstehen die sogenannten „Experimentalwissenschaften“ (als da sind: Physik, Chemie, Geologie, Physiologie, ja auch Psychologie, Ästhetik und Pädagogik [Pädologie]), die in dem wissenschaftlich geleiteten Versuch eine wesentliche methodische Grundlage ihres Untersuchungsverfahrens ausgebildet haben.
Das Experiment ist eine Frage an die Natur. Mit ihm nähert sich der Forscher den Dingen, um von ihnen belehrt zu werden, nicht aber — nach den berühmten Worten Kants — in der Qualität eines Schülers, der sich alles vorsagen läßt, was der Lehrer will, sondern eines bestallten Richters, der die Zeugen nötigt, auf die Fragen zu antworten, die er ihnen vorlegt. Die bloße Beobachtung ergibt nur, was die Natur uns gewissermaßen von selbst hergibt; mit dem Experiment kommen wir dagegen weiter: wir legen ihr Fragen vor und zwingen sie zugleich, uns zu antworten. „L’observateur“, sagt Cuvier, écoute la nature; l’experimentateur l’interroge et la force à se d’évoiler“[18].
Den Zwecken des experimentellen Verfahrens angepaßt hat die Wissenschaft eine zahllose Reihe von Instrumenten und Apparaten ersonnen, die der Aufgabe dienen, die Beantwortung bestimmt formulierter Fragestellungen möglich zu machen. Darin offenbart sich ihr eminent konstruktiver Charakter. Wo das Auge nicht mehr hinreicht, Unterschiede zu empfinden, lehrt das Mikroskop, indem es unsere Sinne verfeinert, noch eine ganze Welt im Kleinen (man denke an die zahlreichen Ergebnisse der modernen Bakteriologie), das Fernrohr eine ganze Welt im Großen. Technische Hilfsmittel dieser[S. 113] Art dienen entweder der qualitativen oder quantitativen Analyse. Wissenschaftliche Erfindungen zum Zweck qualitativer Untersuchungen sind außer den genannten (Mikroskop, Fernrohr) schon das Skalpell des Anatomen, das Vergrößerungsglas, das Spektroskop, ferner alle Spekulatoren (einschließlich der Röntgenröhre), Resonatoren, Analysatoren, Stethoskope. Wissenschaftliche Erfindungen zum Zweck quantitativer Untersuchungen sind alle diejenigen, die ein Messen, Zählen oder Wägen der gefundenen Elemente gestatten, also neben den einfachsten, die in Zentimetermaß und Wage bestehen, kompliziertere wie Ergograph, Sphygmograph, Pneumograph, Plethysmograph, Seismograph, Thermometer, Barometer, Tonometer, Galvanometer, Amperemeter, Voltameter usw. — Eine stattliche Reihe wissenschaftlicher Resultate, die auf Grund experimenteller Analysen gewonnen worden sind, haben ihren Ursprung lediglich dieser konstruktiven Seite des wissenschaftlichen Denkens zu verdanken. Man kann geradezu sagen, daß es dem menschlichen Geiste durch sie gelungen ist, die Grenzen, die der Kraft seiner Sinne gezogen sind, ins fast Unglaubbare zu erweitern. Von der Verbesserung und Verfeinerung der instrumentellen Hilfsmittel der Analyse hängt in rein technischer Hinsicht zu einem großen Teil der künftige Fortschritt der Realwissenschaften ab.
Überall, wo wir die Einzelergebnisse analytischer Untersuchungen zu einem allgemeinen Resultat zusammenfassen, bedienen wir uns einer Methode, die wir nach überliefertem Sprachgebrauch als „synthetisch“ bezeichnen dürfen.
Das synthetische Untersuchungsverfahren hat nur in den Tatsachenwissenschaften die Analyse zu seiner Voraussetzung. In den mathematischen Disziplinen z. B. steigt es von wenigen obersten Begriffsbestimmungen und Axiomen durch deduktives Fortschreiten vermittels syllogistischer Ketten zu einer Fülle von Lehrsätzen herab, die untereinander einen denknotwendigen Zusammenhang solcher Art bilden, daß durch einen Fehler in einer der oberen Prämissen das ganze Gebäude stürzen würde. Aus der Begriffsbestimmung der geraden Linie z. B. (als der kürzesten Verbindung zweier Punkte) sowie aus der Begriffsbestimmung paralleler Geraden (als solcher, die ins Unendliche[S. 114] verlängert, sich nirgends schneiden) folgt unter Zuhilfenahme anderer Lehrsätze auf deduktivem Wege eine Reihe davon verschiedener Bestimmungen, wie z. B. daß Gegen- und Wechselwinkel an Parallelen gleich sind, daß die Summe der Winkel im Dreieck zwei Rechte betrage, daß der Außenwinkel an der Spitze eines Dreiecks gleich der Summe derjenigen Dreieckswinkel sei, die nicht seine Nebenwinkel bilden u. a. m. Das Verfahren des Mathematikers ist also im Prinzip ein synthetisches, und zwar seinem Wesen nach hauptsächlich bestehend aus rational-deduktiven Synthesen[19].
Im Gegensatz dazu ist die Methode der Realwissenschaften, in denen Analyse und Synthese sich zu dem Gesamtverfahren ergänzen, eine im wesentlichen empirisch-induktive. Nur in den genetischen Wissenschaften hat das Einzelne, wie bereits früher angedeutet, an und für sich Wert und Bedeutung einer wissenschaftlichen Erkenntnis, obgleich auch hier ein Fortstreben zum Allgemeinen (Gesamtbegriff aus Spezialbegriffen) durch Abstraktion unverkennbar ist. In den systematischen Disziplinen dagegen ist das Einzelne nur Durchgangspunkt zum Allgemeinen. So suchen Botanik, Zoologie und Mineralogie allgemeine Gattungsbegriffe aus den Bestimmungen über die einzelnen Arten; Physik, Chemie und Physiologie allgemeine Gesetze des Naturgeschehens aus den Bestimmungen über die einzelnen Veränderungen der Natur. Daß sich gerade der Begriff Naturgesetz (nicht: „Geistesgesetz“) als terminus technicus im wissenschaftlichen Denken fest eingeprägt hat, erklärt sich daraus, daß die naturwissenschaftlichen Gesetze an Zahl größer, an objektiver Gültigkeit im allgemeinen gesicherter sind als die der Geisteswissenschaften, obgleich auch in deren systematischen Disziplinen — z. B. den psychologischen, den Staats- und Wirtschafts- sowie den Kunst- und Kulturwissenschaften — allgemeine Gesetze als vorhanden zugestanden werden (z. B. die Assoziationsgesetze in der Psychologie, die Jakob Grimmschen Gesetze der Lautverschiebung in der germanischen Sprachwissenschaft u. a.).
Überall, wo wir in einer beliebigen Menge von Exemplaren auf analytischem Wege solche finden, die in einer größeren Anzahl von Merkmalen übereinstimmen, fassen wir diese — unter Abstraktion von den nichtgemeinsamen Merkmalen — synthetisch-induktiv zu einem Artbegriffe[S. 115] jener Exemplare zusammen. Auf dieselbe Weise werden dann aus Arten Gattungen, aus Gattungen höhere Gattungen usw. (verallgemeinernde Induktion)[20]. Diesem Prozeß induktiver Begriffsbildung entspricht der Prozeß induktiver Gesetzesbildung, der darum logisch damit auf die gleiche methodische Stufe zu stellen ist. Überall, wo wir in einer Reihe von Veränderungen durch analytische Untersuchung die Tatsache finden, daß gewisse Vorgänge gleicher Art (a) immer von gewissen Vorgängen einer anderen Art (b) begleitet oder gefolgt sind, stellen wir das allgemeine Erfahrungsgesetz auf: Immer wenn a, dann b. Dieses ist alsdann der zusammenfassende Ausdruck für die — sei es qualitativen, sei es quantitativen — Beziehungen der beiden Objekte oder Vorgänge. Ein Erfahrungsgesetz besteht also in einem hypothetischen Gefüge, das durch ein induktives Schlußverfahren gewonnen, nur approximative Gültigkeit beanspruchen kann. Beispiele dafür sind besonders in den systematischen Naturwissenschaften in großer Anzahl vorhanden: „Wenn man Wasser bis auf 100° erwärmt, verdampft es; wenn ein Vakuum hergestellt ist, fallen alle Körper mit gleicher Geschwindigkeit; wenn man zwei Körper aneinanderreibt, setzt sich die geleistete mechanische Energie in Wärme um; wenn man zwei Magnete einander nähert, so ist die Kraft, mit der die beiden Pole aufeinander einwirken, direkt proportional der magnetischen Kraft beider Körper, umgekehrt proportional dem Quadrate der Entfernung.“ Andere beliebig herausgegriffene Beispiele bilden: das Weber-Fechnersche psychophysische Grundgesetz; das Gesetz der multiplen Proportionen; die Avogadrosche Regel: das Gay-Lussacsche, das Boyle-Mariottesche Gesetz; Faradays Gesetze der Elektrolyse u. a. m. Alle diese Gesetze (die sprachlich übrigens durchaus nicht immer in Form eines hypothetischen Satzes ausgedrückt zu sein brauchen) sind Wahrscheinlichkeitsgesetze, d. h. ihre Gültigkeit erreicht nur einen — wenngleich bisweilen sehr hohen — Grad der Wahrscheinlichkeit. Sie sind Gesetze, die von der Vergangenheit aus zugleich das Zukünftige vorausbestimmen. Weil bis jetzt immer, wo der Vorgang a gegeben, der Vorgang b gefolgt ist, stellen wir die auch für alles kommende geltende Regel auf, daß immer wo ein a, auch ein b sei. Sie sind also wie ein Wissen des Gewesenen,[S. 116] so auch ein Vorauswissen des Bevorstehenden, entsprechend dem bekannten Worte Auguste Comtes: „Savoir c’est prévoir“ („Wissen ist Vorherwissen“). Und dieses Vorauswissen ist um so sicherer und zuverlässiger, je umfangreicher der Erfahrungsbestand, auf den es sich gründet; je zahlreicher die wirklichen Fälle und Möglichkeiten, die seine Gültigkeit immer erneut bestätigen (Verifikation empirischer Gesetze).
Eine besondere Bedeutung hat in dieser Methode induktiver Gesetzesbildung das Verfahren, wodurch innerhalb einer Mannigfaltigkeit von Vorgängen, die von einer Mannigfaltigkeit anderer Vorgänge gefolgt sind, die als Ursache und Wirkung zusammengehörigen Glieder herausgefunden werden. Hier bildet die Konstanz der Aufeinanderfolge das entscheidende Merkmal für die gesuchte Bestimmung. Wo ein Vorgang b einmal den Vorgängen a c d e, das andere Mal den Vorgängen a f g h und wieder ein anderes Mal den Vorgängen a i k l sowie a m n o usw. folgt, da liegt es nahe zu sagen: a ist die Ursache von b; b die Wirkung von a. Eine solche Bestimmung aber verlangt eine oft wiederholte, sorgfältigste Anstellung von Beobachtungen (die wenn möglich sogar experimentell die Bedingungen des zu untersuchenden Effekts in den verschiedensten Weisen verändern müssen), um aus den in Betracht kommenden Möglichkeiten die wahrscheinlichste herauszufinden. (Ausführliche logische Untersuchungen über die Feststellung empirischer Kausalzusammenhänge in der neueren englischen Logik, vornehmlich bei John Stuart Mill und W. St. Jevons.)
Von den empirischen Gesetzen, die als durch Induktion gewonnen nie mehr als einen — wenngleich oft sehr hohen — Grad der Wahrscheinlichkeit erreichen, sind streng die logischen Gesetze zu scheiden, die — nicht aus, sondern an der Hand der Erfahrung gewonnen — nicht Produkte, sondern (nach den tiefgehenden Untersuchungen Kants) Voraussetzungen (und zwar allgemein- und notwendig-gültige Voraussetzungen) aller Erfahrung bilden. Man hat sie treffend als Gesetze des Empirischen den obenbesprochenen induktiv-gewonnenen als empirischen Gesetzen entgegengestellt (Riehl). Hierhin gehört in erster Linie als oberste materiale Voraussetzung aller Erfahrung: das allgemeine Kausalgesetz (das besagt, daß alles, was ist, eine Ursache hat, durch die es ist, und nichts als ursachslos gedacht werden könne), ferner die dazugehörigen Folgesätze, die besagen, daß aus gleichen Ursachen gleiche Wirkungen, daß aus nichts nichts, daß aus dem Seienden nie ein Nichtseiendes hervorgehen könne. In engem Zusammenhange mit diesen logischen Grundsätzen aller Erfahrung stehen speziellere materiale Prinzipien wie das Gesetz der Erhaltung der Materie von Lavoisier und das Gesetz der[S. 117] Erhaltung der Energie von Rob. Jul. Mayer und Helmholtz, die zusammengenommen besagen, daß die Summe der im Universum vorhandenen Materie und Energien konstant bleibe. Die neuere Logik neigt ihren vornehmlichsten Richtungen nach dazu, auch diese allgemeinen Grundsätze wissenschaftlichen Denkens als logische (d. h. als von der Erfahrung und ihrer aufs Approximative einschränkenden Gültigkeit unabhängige, mithin allgemein- und notwendig-gültige) Gesetze zu deuten; die Diskussion darüber ist indessen zur Zeit noch nicht abgeschlossen.
Wie das menschliche Denken an keinem Punkte seiner Entwicklung zur Ruhe kommt, sondern aus allen Erkenntnissen neue Probleme, aus allen Problemen neue Erkenntnisse zu gewinnen trachtet, so strebt es auch in den Erfahrungswissenschaften über die Feststellung gesetzlicher Zusammenhänge hinaus zu der Frage nach dem Warum der Erscheinung und ihrer Regelmäßigkeit. Einer Erklärung durch Aufzeigung seiner — dem sinnlichen Wahrnehmen entzogenen — Ursachen bedarf nur das Tatsächliche, nicht das Notwendige. Wir fragen nicht, warum 2 × 2 = 4, warum Gleiches zu Gleichem addiert Gleiches ergebe, weil wir unmittelbar gewiß einsehen, daß es so ist; wir fragen nicht, warum das Quadrat über der Hypotenuse im rechtwinkligen Dreieck gleich der Summe der Quadrate über den Katheten sei, wenn wir den logischen Grund dieses zuletzt aus unmittelbar-gewissen Urteilen abgeleiteten, mittelbar gewissen Lehrsatzes eingesehen haben. Wohl aber fragen wir, warum ein Magnet in der Mitte zerbrochen wieder an beiden Bruchstücken am einen Ende einen Nord-, am anderen einen Südpol habe, warum ein in die Lüfte geworfener Körper wieder zur Erde zurückkehre, warum alle Körper des Universums sich nach den Bestimmungen des Newtonschen Gravitationsgesetzes einander anziehen, warum von zwei einmal zusammen in einem individuellen Bewußtsein gegenwärtig gewesenen Inhalten jeder bei seinem erneuten Auftreten die Tendenz habe, auch den anderen wieder hervorzurufen, warum gerade Mitteleuropa und kein anderer Teil der Erde das Mutterland der gesamten neueren Kulturentwicklung geworden sei u. a. m. Wir suchen also — unzufrieden mit der Fixierung der Tatsachen — nach ihrer Erklärung. Daraus entstehen die wissenschaftlichen Theorien, daraus — sofern diese Theorien als unbewiesen oder unbeweisbar nur Wahrscheinlichkeitsgültigkeit haben — die wissenschaftlichen Hypothesen.
Eine wissenschaftliche Theorie ist also eine Lehrmeinung, die eine gesetzlich fixierte Erscheinung des Wirklichen aus ihren dem wahrnehmenden[S. 118] Erkennen entzogenen Ursachen möglichst vollständig und im Einklang mit den bewiesenen Tatsachen der Erfahrung erklärt. So z. B. erklärt die Ampère-Webersche magnetische Molekulartheorie die Bipolarität aller Magnete durch die Annahme, daß auch schon die Moleküle eines Magneten kleinste bipolare Magnete seien; so erklärt ferner die Residualtheorie der assoziativen Reproduktion das Wiederauftreten von Bewußtseinsinhalten infolge der Reproduktion damit assoziierter Inhalte durch die Annahme assoziativ miteinander verflochtener Residuen, die je nach den Hypothesen über das Verhältnis von Leib und Seele als physiologische, psychische oder psycho-physiologische gedeutet werden. Beliebig herausgegriffene Beispiele wissenschaftlicher Theorien sind ferner: die Atomtheorie der Materie (Demokrit; Dalton); die Newtonsche Gravitationstheorie (Annahme einer Schwerkraft zur Erklärung der Anziehung der Weltkörper); die Relativitätstheorie Einsteins; die Quantentheorie Plancks; die James-Langesche Gefühlstheorie; die W. A. Wolffsche Theorie über die Entstehung der Homerischen Epen.
Eine Theorie kann als bewiesen gelten, sofern sie mit allen durch die Erfahrung zureichend begründeten Tatsachen in Einklang steht; sie ist widerlegt, wo sie zu einer oder mehreren dieser Tatsachen in Widerspruch rückt. Allemal also, wo sie eine als gültig gesicherte Tatsache nicht zu erklären weiß, macht sich das Bedürfnis nach einem neuen, besseren Erklärungsversuch fühlbar. So mußten z. B. die geozentrische Theorie des Aristoteles und Ptolemäus der heliozentrischen des Kopernikus, die Newtonsche Emissions- und Huyghenssche Undulationstheorie des Lichtes der elektromagnetischen Lichttheorie von Maxwell und Hertz, die Phlogistontheorie von Stahl und Becher der Lavoisierschen Verbrennungstheorie, die Gallsche Schädellehre sowie die Flourenssche Indifferenztheorie des Großhirns der Lokalisations- oder Zentrentheorie der neueren Physiologen weichen. Andere Theorien liegen — als mögliche, einander ausschließende Erklärungsversuche — lange Zeit hindurch miteinander im Kampfe, bis eine von ihnen — meist die einfachere — als die wahrscheinlichste die anderen verdrängt. Hierhin gehören z. B. die verschiedenen Hypothesen, die das biologische Gesetz von der Variation der Arten erklären (die Darwinsche Selektions-, die Wagnersche Migrations-, die Vriessche Mutationstheorie); ferner die nativistische (Hering) und empiristische (Helmholtz) Theorie vom Ursprung der Raumwahrnehmung; die[S. 119] vitalistischen und mechanistischen Hypothesen zur Erklärung der Lebensvorgänge; die parallelistische und Wechselwirkungstheorie des Verhältnisses von Leib und Seele; die erkenntnistheoretischen Theorien des Idealismus und Realismus, Rationalismus und Empirismus u. a. m.
Der Wert einer wissenschaftlichen Theorie ist im allgemeinen abhängig von ihrer Fruchtbarkeit. Auch später als falsch erkannte Deutungsversuche haben der Wissenschaft unschätzbare Dienste erwiesen, indem sie — eine vorübergehende Beruhigung des Geistes in den brennendsten Fragen gewährend — einen rückhaltlosen Fortschritt der Forschung ermöglichten. Von diesem Standpunkt aus ist selbst fernliegenden, uns heute vielleicht fast abenteuerlich erscheinenden Hypothesen der ihnen zukommende wissenschaftliche Wert nicht abzusprechen. Man nennt solche Erklärungsversuche, die als unbewiesen Jahrzehnte, ja vielleicht Jahrhunderte hindurch die vorübergehende Grundlage der Weiterforschung bilden, Arbeitshypothesen. Arbeitshypothesen in diesem Sinne waren in der älteren Wissenschaft die physiologische Theorie der Lebensgeister, die auf Aristoteles zurückgehend die Physiologie des 17. und 18. Jahrhunderts beherrschte; die Fluida-Theorie der magnetischen und elektrischen Erscheinungen sowie der Nervenerregung, die Mesmersche Theorie des tierischen Magnetismus u. a.; Arbeitstheorien in diesem Sinne sind in der Gegenwart die Atom- und Molekular-, die Ionen- und Elektronentheorie der modernen Physik und Chemie sowie die Parallelismustheorie des Verhältnisses von Körper und Geist in der neueren Psychologie. — „Die Laien sind darüber betroffen“ — sagt H. Poincaré gelegentlich (Wiss. u. Hyp., dtsch., 3. Aufl. 1914, S. 161) —, „wie viele wissenschaftliche Theorien vergänglich sind. Nach einigen Jahren des Gedeihens sehen sie dieselben nacheinander aufgegeben; sie sehen voraus, daß die Theorien, die heutzutage Mode sind, in kurzer Zeit vergessen werden, und sie schließen daraus, daß diese Theorien absolut eitel sind. — Aber ihr Skeptizismus ist oberflächlich; denn sie geben sich keine Rechenschaft von dem Ziele und der Rolle, welche wissenschaftliche Theorien spielen sollen ...“ — Diese Rolle besteht eben darin, gegebene Erscheinungen nach dem jeweiligen Stande der Forschung auf die einfachste und befriedigendste Weise zu erklären und dadurch dem Fortgang der wissenschaftlichen Untersuchungen Tür und Tor zu öffnen.
[S. 120]
Vermöge der logischen Beziehungen, in die die Untersuchungsobjekte eines Forschungszweiges in ihren begrifflichen Grundlagen zueinander treten, schließen sich diese zu einem wissenschaftlichen Begriffssystem zusammen, in dem man von der obersten Gattung jener Objekte nach unten hin bis zu deren niedersten Arten bzw. Exemplaren herabsteigen kann. Das Verfahren, durch das ein solches einheitliches System gewonnen wird, nennt man Klassifikation, die elementaren Akte, durch die es zustande kommt, Einteilung oder Division.
Einen Begriff einteilen heißt: die Arten, die ihm als Gattungsbegriff untergeordnet sind, vollständig und ausführlich aufzählen. Wo man von dem allgemeinsten Begriff des einer Wissenschaft eigenen Untersuchungsobjektes ausgehend (z. B. Tier, Pflanze, seelische Erscheinung) zunächst deren nächstoberste Arten angibt und diese abermals in Arten und ihre Unterarten sowie unterste Arten einteilt, entsteht aus dem Zusammenschluß dieser Einteilungen die Klassifikation und mit dieser das Begriffssystem jener Wissenschaft. So z. B. teilt die Zoologie ihr Untersuchungsgebiet, die Tiere, nach deren begrifflicher Fixierung in zwei Reiche: Protozoen (Urtiere) und Metazoen (mehrzellige Tiere); die letzteren wieder in Kreise, die Kreise in Klassen, diese in Ordnungen, diese wieder in Familien, diese in Geschlechter, Gattungen, Arten und Unterarten. Man kann Zoologie, Botanik und Mineralogie um ihres wesentlich klassifizierenden Charakters willen geradezu als klassifikatorische Wissenschaften bezeichnen, im Gegensatz zur Physik, Chemie und Physiologie, die in geringerem Maße als jene aus dem Einzelnen zu Arten und Gattungen, in stärkerem Grade zu allgemeinen Regeln und Gesetzen, nach denen sich das Einzelne vollzieht, fortschreiten.
Eine Einteilung ist nach den Elementen der Logik eine erschöpfende divisive Urteilsverbindung (S ← [teils P1, teils P2, teils P3]), die infolge der Vollständigkeit ihrer Glieder (membra divisionis) rein umkehrbar sein muß (z. B. „Die Wirbeltiere sind teils Fische, teils Lurche, teils Kriechtiere, teils Vögel, teils Säugetiere“, also: „Fische, Lurche, Kriechtiere, Vögel und Säugetiere sind die Wirbeltiere“). Weitere Beispiele sind: „Die pathologischen Verbiegungen der Wirbelsäule[S. 121] sind teils kyphotische, teils lordotische, teils skoliotische; die Inhalte des Bewußtseins sind teils gegenständliche, teils zuständliche.“ Die Einteilungsglieder umfassen — soll die Einteilung formal gültig sein — den ganzen Umfang des eingeteilten Begriffes; sie sind ferner einander nebengeordnet sowie nach einem und demselben logischen Prinzip (principium divisionis) aufgestellt.
Sind die Einteilungsglieder nicht einander nebengeordnet, sondern neben den wesentlichen Arten auch unwesentliche oder abgeleitete oder gar neben eigentlichen Arten auch diesen untergeordnete Arten oder Exemplare mit aufgeführt, dann ist die Einteilung zu weit, mithin formal ungültig und darum falsch. Und weiter: sind die Einteilungsglieder nicht nach einem und demselben Gesichtspunkt gewählt, sondern darin verschiedene Gesichtspunkte durcheinander gebracht (so z. B. wenn man die Gattung „Mensch“ in einer und derselben Einteilung teils nach ihrer Haarfarbe, teils nach ihrer Gesichtsfarbe scheidet), dann ist gleichfalls die Einteilung als Ganzes formal ungültig, mithin falsch. Nach einem und demselben Gesichtspunkt einteilen heißt: die Scheidung einer Gattung in ihre Arten nach einer und derselben Art der Merkmale vornehmen, z. B. beim Menschen entweder nach körperlichen Merkmalen, wie Schädelbildung, Hautfarbe, Größe (also anthropologischen), oder nach sozialen, wie Nationalität, Abstammung, Beruf, Vermögenslage (also soziologischen), oder nach geistigen, wie Intelligenz, Charakter, religiöser Glaube (psychologischen Eigenheiten). Linné schuf sein Pflanzensystem nach der Verschiedenheit in der Ausbildung der männlichen und weiblichen Fortpflanzungsorgane der Pflanzen (Sexualsystem), Bernard de Jussieu (sowie sein Neffe Antoine) nach der Verschiedenheit im Bau der Blüte (das „natürliche System“). Cuvier klassifizierte die Tiere nach der Verschiedenheit ihres Knochenbaus; Blainville nach der ihrer Körperbedeckung.
Nicht nur die systematischen, auch die genetischen Disziplinen bedienen sich des Verfahrens der Einteilung, mithin der Klassifikation. Der Historiker zerlegt seinen Gegenstand, die Weltgeschichte, in Zeitalter (Altertum, Mittelalter und Neuzeit), diese wieder in Perioden und Zeitabschnitte; der Biologe die Entwicklungsgeschichte der Organismen, der Psychologe die Entwicklung des Seelischen in einzelne Stufen, die sich als Glieder aus dem Gesamtzusammenhange herausheben.
[S. 122]
Je nach dem Verhältnis der Glieder einer Einteilung zueinander sind diese entweder wohl-begrenzende oder Typeneinteilungen. Wohlbegrenzende Einteilungen sind solche, deren Glieder — meist durch Unterschiede qualitativer Art — scharf voneinander getrennt sind (Beispiele dafür finden sich besonders in der Mathematik, Botanik, Zoologie, Mineralogie, wohl auch Chemie); Typeneinteilungen sind solche, deren Glieder miteinander in fließendem Zusammenhange stehen, so daß ihre Grenzen durch — nicht qualitativ, sondern graduell voneinander verschiedene — Zwischenstufen und Übergangsformen teils kontinuierlicher, teils diskontinuierlicher Art ausgefüllt werden. (Beispiele dafür sind Leibniz’ Scheidung der endlichen Monaden in nackte, Seelen und Geister sowie der diesen entsprechenden Perzeptionen; die biogenetischen Annahmen über die Entwicklungsstufen des organischen Lebens; die geläufig-gewordene Scheidung der Menschen nach ihren Rasseeigentümlichkeiten, als da sind: arisch-germanisch, slawisch, semitisch, mongolisch).
Wie die Definitionen wissenschaftlicher Begriffe und mit ihnen die Tatsachenwissenschaften selbst nichts Feststehendes, sondern ein sich ständig Wandelndes bilden, so sind auch die Einteilungen einer Wissenschaft immer nur relativ- (d. h. für den Stand der Forschung ihrer Zeit und auch das nicht einmal stets allgemein) gültig. Ein naheliegendes Beispiel dafür bilden die Klassifikationsversuche des Begriffes „Wissenschaft“ selbst, die seit dem Altertum (Platon, Aristoteles, Stoa), von Bacon zu d’Alembert und Comte sowie weiter bis zu neueren Versuchen von Spencer, Wundt, Erdmann u. a. immer veränderte Formen und Gestalten angenommen haben. Ein weiteres berühmtes Beispiel für den Wandel wissenschaftlicher Klassifikationen bildet die Geschichte der Einteilung des Seelischen, die von Platons Lehre von den Seelenteilen (Verstand, Gemüt, Begierde) sowie von Aristoteles’ Scheidung der repräsentativen Stufen der seelischen Entwicklung (Ernährung; Empfindung; Denken) über Descartes und Locke (Denken und Wollen) zur Wolffschen Lehre von den beiden Seelenvermögen (Erkennen und Begehren) und von da weiter über Sulzers, Mendelssohns und Tetens’ Dreiteilung (Denken, Fühlen und Wollen) bis zu den mannigfachen Versuchen der Gegenwart führt, die Vielheit der seelischen Erscheinungen entweder in zwei, drei oder vier Hauptarten zu zerlegen oder sie gar auf ein Urelement (z. B. das Wollen nach der Lehre der Voluntaristen) zurückzuführen.
[16] Auf die speziellen Differenzen zwischen den methodischen Voraussetzungen naturwissenschaftlicher und psychologischer Forschung kann bei dieser summarischen Übersicht über die Haupttatsachen nicht eingegangen werden. Man vgl zur Methodenlehre der Psychologie Arbeiten von Ebbinghaus, Münsterberg, Stumpf; sowie: Sigwart, Logik Bd. II.
[17] „Die Begriffsbestimmung erfolgt durch (Angabe der) nächsthöheren Gattung und der spezifischen Verschiedenheit.“
[18] „Der bloße Beobachter belauscht die Natur; der Experimentator befragt sie und zwingt sie, sich zu enthüllen.“
[19] Auf die mannigfachen methodologischen Probleme des mathematischen Denkens kann hier naturgemäß nicht eingegangen werden; vgl. dazu die Literaturnachweise am Schluß.
[20] Dem analog ist das Verfahren, durch das wir das Gesamtbild einer Persönlichkeit oder eines Einzeldinges aus seinen speziellen Seiten gewinnen (Gesamtbegriff aus Spezialbegriffen durch ergänzende Induktion).
[S. 123]
Ein wissenschaftliches System ist ein Inbegriff von zureichend begründeten Behauptungen und Problemfragen über einen Teil des Wirklichen, die untereinander in engem logischen Zusammenhange stehen.
Wo wir im Fortgange der wissenschaftlichen Untersuchung auf Erkenntnisse stoßen, deren Gültigkeit als zweifelhaft erscheint, da pflegen wir diese zunächst in Form von Fragen zu formulieren, die damit — als wissenschaftlich-gerichtete — zu Problemen werden.
Auch Problemfragen bedürfen wie Urteile einer zureichenden Begründung. Eine Frage ist logisch zureichend begründet, wenn sie richtig gestellt ist, d. h. wenn ihre Voraussetzungen dem jeweiligen Stande der Forschung entsprechen und sie sich folgerichtig aus der bisherigen Entwicklung der Wissenschaft ergibt. Eine Fragestellung ist demnach als falsch zu bezeichnen, wenn sie sich auf Voraussetzungen gründet, die durch die Geschichte der Forschung widerlegt und damit überwunden sind. Es hat keinen Sinn mehr, gegenwärtig etwa im Sinne der scholastischen Philosophie zu fragen, ob die Universalia ante oder post res seien[21]; keinen Sinn mehr, zu fragen, ob die Welt geschaffen oder von Ewigkeit vorhanden, der Geist ein einfaches oder zusammengesetztes Wesen, ob die Gottesvorstellung der Seele angeboren oder von ihr erworben sei. Diese Fragen sind für unsere Zeit anachronistisch, d. h. in ihren Grundlagen einer überholten Zeitperiode angehörend. Wer sie heute noch ernstlich erörtern wollte, indem er sich über alles hinwegsetzte, was die Jahrhunderte zu ihrer Kritik beigebracht haben, der unternähme von vornherein ein fruchtloses und darum überflüssiges Tun. Daraus erhellt der Wert historischer Studien auf wissenschaftlichem Gebiete und mit dem Werte zugleich deren Notwendigkeit.
Es ist eine oft betonte Forderung, daß man in allen wissenschaftlichen Bestrebungen nicht nur wissen müsse, was man zu urteilen, sondern[S. 124] auch, was man zu fragen habe. Von der Aufstellung begründeter Problemfragen hängt in der Tat der Fortschritt der Forschung ab. Wie jedes neue Problem neue Erkenntnisse, so gebärt jede neue Erkenntnis neue Probleme. Die Geschichte hat gelehrt, daß mit der Fülle des Wissens auch der Abgrund des Nichtwissens ins immer Unermeßlichere wächst. Indem wir dem uns innewohnenden, unwiderstehlich vorwärtsstrebenden Kausalbedürfnis willig oder nichtwillig folgen, kommen wir überall bis zu letzten Fragen der Wissenschaft, denen gegenüber der Forscher entweder resigniert sein „ignoro, ignorabo“ spricht[22], oder deren Lösung mehr dem Glauben als dem Wissen anheimfällt. Hierhin gehören Fragen wie die nach dem ersten Ursprung des organischen Lebens, nach der Entstehung des Bewußtseins innerhalb der Entwicklung organischer Wesen, nach der Erklärung des Todes oder des Überganges vom Organischen zum Anorganischen, ja auch schließlich die Fragen nach dem Verhältnis des Geistigen zur körperlichen oder räumlich-ausgedehnten Welt, nach der Natur der Gedächtnisgrundlagen, der Natur des Vererbungsvorganges u. a. m.
Wissenschaftliche Urteile bedürfen allemal dann eines Beweises, wenn ihre Gültigkeit nicht unmittelbar gewiß ist. Über die Frage freilich, ob und wann das der Fall ist, herrscht im einzelnen — wie auch unter den Logikern im Prinzipiellen — Streit. Insbesondere in der Auffassung der Grundlagen der Mathematik ist es neuerdings zu heftigen Kontroversen gekommen, und zwar dadurch, daß die einen — so z. B. John Stuart Mill, in Deutschland Herm. v. Helmholtz — lehren, die Axiome der Geometrie und Arithmetik seien Erfahrungswahrheiten (und zwar als solche durch verallgemeinernde Induktion gewonnen), die anderen, die Axiome der Geometrie und Arithmetik seien zwar an der Hand sinnlicher Wahrnehmungen entwickelt, in ihrer Gültigkeit aber — davon völlig unabhängig — unmittelbar-, darum notwendig- und allgemein-gewiß. Ohne auf das verwickelte Problem der logischen Bedeutung der mathematischen Axiome näher einzugehen, sei doch dazu bemerkt, daß die Millsche Theorie als unhaltbar gelten muß, weil sie die Frage nach dem psychologischen Ursprung mit der nach dem Wesen der mathematischen Axiome verwechselt. Die Frage nach der Entstehung eines Urteils ist eine[S. 125] quaestio facti (Tatsachenfrage); die Frage nach der Art seiner Gültigkeit eine quaestio juris (Rechtsfrage). Wohl sind Axiome wie: „Zwischen zwei Punkten ist die Gerade der kürzeste Weg“ psychologisch-genetisch genommen an der Hand sinnlicher Anschauungen entwickelt; sie sind darum logisch aber nicht Erfahrungserkenntnisse, sondern in ihrer Gültigkeit völlig unabhängig von dieser notwendig- und allgemein-gewiß — entsprechend der vortrefflichen Einsicht Kants, daß zwar alle Erkenntnis mit Eindrücken der Sinne anfange (exordium), nicht aber auch alle aus den Sinnen entstamme (origo). Die mathematischen Axiome sind mithin als Verstandeswahrheiten im Sinne Leibniz’, als synthetische Urteile a priori im Sinne Kants, in ihrer Gültigkeit unmittelbar-gewisse und darum unbeweisbare Wahrheiten, eines Beweises weder fähig noch bedürftig.
Ein wissenschaftlicher Beweis ist logisch dasjenige Verfahren, wodurch ein wissenschaftliches Urteil in seiner Gültigkeit zureichend begründet wird. Die zureichende Begründung erfolgt entweder durch den Hinweis auf die Tatsachen der Wahrnehmung (hinweisende Begründung) oder durch Ableitung des zu beweisenden Urteils als Konklusio aus seinen Gründen als Prämissen (ableitende Begründung). So z. B. geschieht die zureichende Begründung mathematischer Definitionen wie etwa der Begriffe Dreieck, Kreis, Parallelogramm, Pyramide usw. durch den Hinweis auf die Daten der Wahrnehmung bzw. auf die dieser immanenten psycho-physiologischen Gesetze der Raumanschauung; die zureichende Begründung mathematischer Lehrsätze sowie der meisten Tatsachenurteile durch Ableitung (Reduktion) aus anderen unmittelbar-gewissen oder bereits zureichend-begründeten Urteilen, sei es unmittelbar oder mittelbar, auf deduktivem, induktivem oder dem Wege der Ähnlichkeitsschlüsse. Urteile wie: „Die Farbe dieser Blätter ist gelb; die Oberfläche dieser Frucht ist rauh“ sind durch Hinweis zureichend begründet, wenn einem jeden die Möglichkeit, sich von ihrer Wahrheit zu überzeugen, unmittelbar gegeben ist; sie bedürfen aber einer induktiv-ableitenden Begründung, wenn die Möglichkeit einer Nachprüfung durch Wahrnehmung nicht mehr gegeben, der Beweis vielmehr auf die zeitlich weiter zurückliegenden, übereinstimmend-überlieferten Wahrnehmungen anderer Individuen gestützt ist (S1 gibt an, daß Q ← R, S2 gibt an, daß Q ×;R, S3 gibt an, daß Q ← R usw.; also wird Q ← R wahr sein; ein sogenannter „Indizienbeweis“). Der[S. 126] Indizienbeweis spielt — abgesehen von seiner praktischen Anwendung in der Rechtswissenschaft — besonders im historischen Denken eine wesentliche Rolle, wo auf Grund der übereinstimmenden Angaben mehrerer Quellen — unter Abstraktion von den davon abweichenden — von zwei oder mehreren möglichen Begebenheiten die eine als den Tatsachen entsprechend mit mehr oder minder großer Wahrscheinlichkeit angenommen wird.
Als Arten des auf Ableitung beruhenden wissenschaftlichen Beweisverfahrens unterscheidet die traditionelle Logik den direkten und indirekten, den progressiven und regressiven Beweis. Direkt erfolgt die Ableitung, wenn die Wahrheit des zu Beweisenden (demonstrandum; Thesis) sich in ununterbrochener logischer Folge aus der Wahrheit seiner Gründe (rationes demonstrandi) ergibt (Behauptung: wahr S ← P; Bew.: wahr S ← M, wahr M ← P, also wahr S ← P); indirekt (oder apagogisch) erfolgt die Ableitung, wenn die Wahrheit des zu Beweisenden sich aus der zureichend begründeten Falschheit seines kontradiktorischen Gegenteils ergibt (deductio ad absurdum; Beh.: wahr S ← P; Bew.: Angenommen S ← P nicht wahr, dann wäre Q ← R wahr; nun ist Q ← R, wie sich beweisen läßt, falsch; also ist es auch falsch, daß S ← P nicht wahr sei; mithin S ← P wahr). — Progressiv heißt eine Ableitung, die, wie im direkten Beweis, von der Wahrheit der Gründe auf die Wahrheit der Folge, regressiv diejenige, die — wie im indirekten Beweis sowie einer viel gebrauchten Form wissenschaftlicher Widerlegung — von der Falschheit der Folge auf die Falschheit der Gründe geht (z. B. Widerlegung in regressiver Form: Beh.: S ← P falsch; Bew.: wenn S ← P wahr, dann Q ← R wahr; nun läßt sich beweisen, daß Q ← R nicht wahr, also ist es falsch, daß S ← P wahr; mithin: S ← P falsch). Die Widerlegung ist demnach die zureichende Begründung der Falschheit eines Urteils, wie der Beweis die zureichende Begründung der Wahrheit; sie erfolgt progressiv durch die zureichende Begründung der Wahrheit des dem zu widerlegenden kontradiktorisch-entgegengesetzten Urteils.
Ein anderes ist es, wissenschaftliche Wahrheiten finden, ein anderes, sie beweisen. Maxwell stellte die elektromagnetische Lichttheorie auf; Hertz bewies sie, und zwar auf induktivem Wege durch eigens von ihm erdachte Experimente. Wohl können gelegentlich der[S. 127] Weg, auf dem man zu einer Erkenntnis gelangt, und derjenige, auf dem man sie zureichend begründet, der Sache nach miteinander übereinstimmen; in der Regel aber (und das gilt besonders für die großen, weittragenden Entdeckungen der Tatsachenwissenschaften) ist der Gedanke da, ehe auch nur ein Teil seiner Gründe annähernd übersehen werden kann (ähnlich Riehl, Robert Mayers Entdeckung und Beweis des Energieprinzips, Philos. Abh., Sigwart gew., 1910, S. 162).
In einem vollständigen System der Wissenschaft hängen alle Urteile dergestalt mit- und untereinander zusammen, daß jede neue Einsicht, die sich mit den bereits bestehenden in Übereinstimmung befindet, darin logisch ihre Stütze findet, jede aber, die dem vorhandenen Bestand der Erkenntnis widerspricht, von vornherein den Verdacht der Falschheit erweckt. Die Einheit der Wissenschaft verlangt, daß alle Erkenntnisse — gleich wie — in einem geordneten Zusammenhang stehen, in dem man von dem Allgemeinsten bis zu dem Speziellsten und umgekehrt hinauf und hinab steigen kann, ohne innerhalb der systematischen Ordnung des Ganzen auf Widersprüche zu stoßen. Ergibt der Fortgang der Forschung an irgendeinem Punkte Erkenntnisse, die entweder an sich selbst oder in ihren Folgen mit den früher gewonnenen nicht in Einklang stehen, so schließen wir daraus, daß entweder diese — die neuen — oder jene alten falsch sind, mithin daß der ganze Weg der Untersuchung einer sorgfältigen Nachprüfung bedarf. Solche Generalrevision der Wissenschaft von ihren letzten Fundamenten aus findet sich, wie die Geschichte der Wissenschaften lehrt, in den meisten Disziplinen (auch hier bis zu einem gewissen Grade mit Ausnahme der mathematischen Forschung) von Zeit zu Zeit immer wieder, und das, wie es scheint, nicht zum Nachteil, sondern zum Segen der Gesamtentwicklung des Wissens. Eine solche Generalrevision von ihren fundamentalen Grundlagen aus macht z. B. gegenwärtig die Physik durch, seit neuere Ergebnisse auf dem Gebiete der Elektrizitätslehre die Aufgabe der alten Hypothese des Äthers nahegelegt haben; eine solche Generalrevision hat gegen Ende des 18. Jahrhunderts die Philosophie durchgemacht, als Kant bewies, daß die Prinzipien der reinen Vernunft nur im immanenten Gebrauch für Erfahrungsobjekte, nicht aber im transzendenten unabhängig von der Erfahrung für die Erkenntnis des Seienden an und für sich Gültigkeit hätten, und damit die Metaphysik von einer kritiklosen Verstandeserkenntnis des objektiven Seins zu einer objektiven Kritik des Verstandes[S. 128] und seiner Anwendung auf die empirische Wirklichkeit umgestaltete[23].
Die Auffindung der wissenschaftlichen Beweisgründe, die eine gleichwie gewonnene Lehrmeinung als gültig erweisen sollen, richtet sich nach dem speziellen Charakter jener Erkenntnis, sowie demjenigen ihres wissenschaftlichen Gebietes überhaupt. Bei mathematischen Einsichten gewährt zumeist schon der Weg ihrer Entdeckung wertvolle Anhaltspunkte für die Aufstellung ihrer zureichenden Begründung. Hier hat jede Bemühung um einen Beweis die Prämissen zu suchen, aus denen sich der zu begründende Lehrsatz notwendig als Konklusio ergibt, und zwar dergestalt, daß die zu beweisende Lehrmeinung mit dem bereits bewiesenen und darum als gewiß erkannten bisherigen Bestande der Forschung so zusammenhängt, daß sie sich als notwendige Konsequenz aus jenem und zugleich darin unlösbar verankert erweist (deduktiver Beweis). Deduktion als Forschungsmethode und Deduktion als Beweismittel unterscheiden sich mithin nur insofern, als die erstere von den Prämissen aus die Konklusio, die zweite von der Konklusio aus die Prämissen sucht.
Analoges gilt für die Beweisführung in den Wissenschaften von Tatsachen. Sei es, daß wir ein einzelnes Faktum der Geschichte, eine allgemeine Regel des Naturgeschehens oder den Erklärungsversuch einer empirisch gesicherten Erscheinung des Wirklichen als wahr zu beweisen suchen, immer haben wir diese als die zu beweisenden Lehren in der Form von Schlußurteilen aus gewissen ihnen als Stütze dienenden Einzelerkenntnissen (als Prämissen) durch eine verallgemeinernde oder ergänzende Induktion (oder auch durch einen Schluß aus hinreichender Ähnlichkeit [Analogieschluß]) mit dem höchstmöglichen Grad der Wahrscheinlichkeitsgeltung herzuleiten. Daß Heinrich IV. im Jahre 1077 in der Tat seinen Bittgang nach Canossa getan hat, beweisen wir induktiv aus den im wesentlichen übereinstimmenden Angaben der wichtigsten Quellenschriften jener Zeit. Daß Körper verschiedenen Gewichts im luftleeren Raum mit gleicher Geschwindigkeit fallen, beweisen wir gleichfalls induktiv aus den übereinstimmenden Ergebnissen zahlloser Versuche, die wir angestellt haben und zur Verifikation (Gültigkeitsbestätigung) jenes Gesetzes jederzeit[S. 129] wiederholen können. Daß endlich die atomistische Theorie der Materie zur Erklärung der Bewegungserscheinungen der Körperwelt gültig sei, beweisen wir wiederum induktiv daraus, daß sie mit allen den einzelnen Faktoren, die hierhin gehören, in Einklang steht und für sie alle einen befriedigenden Maßstab zur Erklärung darbietet (Induktionsbeweis).
Das schwächste wissenschaftliche Beweismittel, das wir besitzen, ist da gegeben, wo wir die Gültigkeit eines Urteils lediglich auf die Ähnlichkeit seines Subjekts zu einem seinen Merkmalen nach ausreichend bekannten Objekte der Forschung aufbauen (Analogiebeweis). Beispiele dafür sind bereits bei der Besprechung der Analogieschlüsse gegeben worden. Hier hat die Auffindung der Beweisgründe den Weg zu gehen, daß sie Objekte sucht, die dem Subjekt des zu beweisenden Urteils wesentlich ähnlich und durch dasselbe Prädikat gekennzeichnet sind, das von jenem als gültig behauptet wird (Behptg.: wahr S ← P; Bew.: S ← M ähnlich und M ← P). Daß diese Beweisführung gegenüber den anderen Formen den geringsten Grad der Sicherheit ergibt, lehrt schon die Geschichte der Wissenschaften unzweideutig. Wie hätte sonst seit Rorarius, Descartes und Malebranche bis zur Gegenwart fort ein jahrhundertelanger Streit darüber entbrennen können, ob die Tiere beseelt seien wie wir Menschen oder aber als seelenlose Automaten, gewissermaßen als Reflexmaschinen, aus Gottes Hand ihr Dasein empfangen hätten.
Die Auffindung der Beweisgründe geht also, wenn wir kurz das Gesagte zusammenfassen wollen, dreierlei Wege: sie sucht das Allgemeine, wo sie daraus das Besondere zu begründen vermag (Deduktion); sie sucht das Besondere, wo sie daraus das Allgemeine ableiten kann (Induktion); und sie sucht das einander Ähnliche, wo sie daraus schließen darf, daß dem einen als Prädikat zukommen wird, was in dem anderen mit zureichender Begründung prädikativ enthalten ist (Analogiebeweis).
Falsche oder unzulängliche Beweise beruhen immer auf falschen oder unzulänglichen Ableitungen. Man nennt sie daher Falschschlüsse (fallaciae); und diese wiederum, sofern sie absichtlich erfolgen: Sophismen (Trugschlüsse); sofern unabsichtlich: Paralogismen (Fehlschlüsse, Vernunftwidrigkeiten). Ein Beweis ist unzulänglich,[S. 130] wenn er nicht die Wahrheit des zu beweisenden Urteils begründet, sondern vielmehr: entweder zu viel oder zu wenig (Beweisverrückung; Heterozetesis) oder auch: ein von dem zu beweisenden völlig verschiedenes Urteil (mutatio elenchi: μετάβασις εἰς ἄλλο γένος). Ein Beweis ist falsch, wenn entweder einer der Beweisgründe falsch (materialer Falschschluß; πρῶτον ψεῦδος), oder aber wenn die Ableitung der Konklusio aus den Prämissen formal ungültig ist (formaler Falschschluß).
Ein unzulänglicher Beweis ist genau genommen gar kein Beweis. Der Versuch, ein Urteil als bewiesen auszugeben, während aus den dafür aufgeführten Beweisgründen in Wahrheit ein ganz anderes folgt, wird logisch eine Erschleichung (subreptio) oder Abirrung des Beweises (aberratio elenchi) genannt. Eine alte Schulregel der Logiker besagt: „Qui nimium probat, nihil probat; qui parum probat, nihil probat“ (wer zu viel oder zu wenig beweist, beweist gar nichts). „Zu viel beweisen“ heißt dabei: etwas als einer Gattung zugehörig nachweisen, was nur für eine Art oder für ein Individuum gültig bewiesen werden soll (denn das Individuum könnte immerhin eine Ausnahme von jener Gattungsregel bilden); „zu wenig beweisen“ heißt: etwas als einer Art zugehörig nachweisen, was für deren Gattung gültig zu beweisen wäre (denn jenes Merkmal könnte ja eine der artbildenden spezifischen Differenzen sein, die der Gattung nicht zukommen).
Daß, wenn eine der Prämissen falsch (bzw. ungewiß), bei formal gültiger Ableitung auch die Konklusio falsch (bzw. ungewiß) ist, bedarf keiner näheren Erläuterung. Ebensowenig daß bei wahren Prämissen kein gültiger Beweis zustande kommt, wo ein formaler Fehler im Schlußverfahren vorliegt. Der geläufigste formale Falschschluß beruht auf dem sog. circulus vitiosus (Zirkelbeweis; petitio principii), der da gegeben ist, wo das zu beweisende Urteil (an sich selbst oder in einer seiner Folgen) irgendwie mit in die Beweisgründe aufgenommen ist, die insgesamt gerade dazu dienen sollen, ebendieses zu erhärten. Ein lehrreiches Beispiel dafür bietet sich in den grundlegenden Deduktionen der Cartesianischen Philosophie: An der Hand seiner Generalregel, daß alles klar und deutlich Erkannte wahr sei, beweist Descartes, daß Gott existiere; und auf die Frage, warum denn alles klar und deutlich Erkannte wahr sein müsse, antwortet er wiederum (man beachte den Zirkel!), weil Gott kein Betrüger sein könne! —
[S. 131]
Der häufigste formale Fehler des syllogistischen Schlußverfahrens kommt zustande durch die sog. quaternio terminorum (Vierzahl der Begriffe), die dann gegeben ist, wenn der Mittelbegriff in der oberen Prämisse in anderer Bedeutung genommen wird wie in der unteren (fallacia medii termini). An die Stelle der Identität des Begriffes, die ja von der sprachlichen Formulierung des Gedankens einigermaßen unabhängig ist, tritt hier also die Identität des Wortes, verbunden mit einer Mehrdeutigkeit seines Bedeutungsinhaltes (Äquivokation). Beispiele für diese Beweisverirrung, die gelegentlich die sinnloseste Form annehmen kann (mittels deren in der Tat alles zu „beweisen“ möglich ist), finden sich insbesondere in den Trug- und Fangschlüssen der griechischen Eristik und Sophistik in reicher Anzahl. Ein Musterbild dieser (nach Prantl von den Megarikern geprägt) bildet:
|
Behauptung: Die Homerische Dichtung ist eine geometrische Figur.
|
|
|
Beweis:
|
Alle Kreise sind geometrische Figuren.
|
|
Die Homerische Dichtung ist ein Sagenkreis.
|
|
|
also ist die Homerische Dichtung eine geometrische
Figur.
|
|
Spezielle Formfehler des induktiven und Analogiebeweises bilden voreilige Verallgemeinerung (wenn der Gattung ein Prädikat beigelegt wird, das bis dahin nur für einen sehr kleinen Teil seiner Arten als gültig erwiesen ist[24]) sowie vorschnelle Schlußfolgerung auf Grund unzureichender Ähnlichkeit. Beispiele induktiver (I) und analogiemäßiger Fehlschlüsse (II) sind:
|
I.
|
|
Lysias war ein großer Redner.
|
|
Demosthenes war ein großer Redner.
|
|
Äschines war ein großer Redner.
|
|
.......
|
|
Alle Griechen werden große Redner gewesen sein.
|
|
II.
|
|
Kirschen schmecken süß und angenehm.
|
|
Tollkirschen sind den Kirschen ähnlich.
|
|
Tollkirschen werden süß und angenehm schmecken.
|
Was sich psychologisch als eine Übertreibung auf Grund der Affekte der Hoffnung oder Furcht, das stellt sich logisch als ein übereilter Induktionsschluß —; was sich psychologisch als eine Verwechslung auf Grund ähnlicher Merkmale, das stellt sich logisch als ein verfehlter Analogieschluß dar.
[S. 132]
Vor einem mannigfach verwickelten und nicht leicht aufzulösenden Problemkreis steht die neuere Logik gegenüber methodischen Hilfsmitteln der Art, wie sie in den Fiktionen und Utopien des wissenschaftlichen Denkens gegeben sind.
Eine wissenschaftliche Fiktion ist die in bestimmter wissenschaftlicher Absicht vollzogene Annahme, daß einem gegebenen Urteil Gültigkeit zukomme, verbunden mit dem Bewußtsein seiner tatsächlichen Ungültigkeit. In dieser Begriffsbestimmung ist auf das Merkmal der Absichtlichkeit besonderes Gewicht gelegt. Soweit eine Einteilung auf diesem noch wenig untersuchten Gebiete logischer Forschung bereits möglich ist, glaube ich, nach dem Gesichtspunkte ihres Zweckes dreierlei Fiktionen unterscheiden zu müssen, und zwar: prüfende, erläuternde und beweisende Fiktionen. Von diesen kommt nur den letzteren im wissenschaftlichen Denken eine größere Bedeutung zu, während die beiden ersten demgegenüber als weniger wichtig zurücktreten.
Als Beispiele prüfender Fiktionen können diejenigen angesehen werden, die den Nicht-Euklidischen Geometrien Lobatschewskijs und Riemanns zugrunde liegen. Es ist kennzeichnend für die logische Funktion der Fiktionen, daß Lobatschewskij (ähnlich wohl schon früher Gauß) die Annahme der Ungültigkeit des Euklidischen Parallelenaxioms nicht vollzogen hat, um damit eine neue geometrische Wissenschaft zu entdecken, sondern vielmehr in der Absicht, das Parallelenaxiom Euklids durch einen indirekten Beweis zureichend zu begründen (beweisende Fiktion). Erst dadurch, daß sich der gesuchte Widerspruch, aus dem die Gültigkeit des in Rede stehenden Grundsatzes gefolgt wäre, nicht ergab, entwickelte sich dann auf der Grundlage der aufgestellten Fiktion die Lobatschewskijsche Geometrie. Verwandtes gilt mutatis mutandis für die Nicht-Euklidische Geometrie Riemanns; nimmt nämlich Lobatschewskij an, daß — abweichend von der Lehre Euklids — zu einer Geraden in einer Ebene durch einen Punkt nicht eine, sondern mehrere Parallelen — so Riemann, daß durch einen Punkt zu einer Geraden in einer Ebene gar keine Parallelen gezogen werden können. Unter der Voraussetzung des Lobatschewskijschen Satzes ergibt sich dann eine formal-logisch konsequente Geometrie, in der die Winkelsumme im Dreieck kleiner,[S. 133] unter der Voraussetzung des Riemannschen eine solche, in der die Winkelsumme im Dreieck größer ist als zwei Rechte. Beide Geometrien wurzeln nun ersichtlich in Annahmen, die dem Euklidischen Parallelenaxiom als einem logisch entwickelten Grundgesetz unserer Raumanschauung widersprechen. Indem diese hier zur Prüfung ihrer Konsequenzen als gültig vorausgesetzt werden, zugleich mit dem unzweideutigen Bewußtsein ihrer faktischen Ungültigkeit, kann man sagen, daß die Nicht-Euklidischen Geometrien der genannten Mathematiker auf prüfenden Fiktionen beruhen.
Die erläuternden Fiktionen bedürfen nur kurzer Besprechung. Sie dienen, wie der Name besagt, als bloße technische Hilfsmittel der Darstellung dazu, aufgestellte wissenschaftliche Lehrmeinungen (seien es Einzelurteile, Gesetze oder Theorien) durch denkmögliche Vorstellungen von Objekten, die aber in ihrer Realität als nichtwirklich bewußt sind, zu erläutern. Hierhin gehören die Leibnizsche Fiktion eines überlegenen Geistes, der — fähig, in dem gegenwärtigen Seelenzustande einer endlichen Monade zu lesen — darin Vergangenheit, Gegenwart und Zukunft des gesamten Universums läse; hierhin die Cartesianische Fiktion eines Dämons, der etwa den menschlichen Intellekt gerade in dem täuschen könnte, was ihm — als klar und deutlich erkannt — zweifelsfrei wahr erscheint, ein Selbsteinwurf, der dazu dient, zu zeigen, wie erhaben über alle Bedenken die Wahrheit sei, die durch das reine Licht des Geistes (lumen naturale) ihre Bürgschaft empfange.
Beweisende Fiktionen weist die Geschichte des wissenschaftlichen Denkens zahlreich auf. Sie dienen — ungeachtet ihrer ziemlich geringfügigen Argumentationskraft — meist dazu, aufgestellte Theorien, also Erklärungsversuche, durch den Nachweis ihres widerspruchslosen Zusammenstimmens mit den empirisch gesicherten Tatsachen zureichend zu begründen; im umgekehrten Falle, sie zu widerlegen (widerlegende Fiktionen). Beispiele der ersteren sind die Rousseausche Fiktion eines reinen (d. h. von aller Kultur unberührten) Naturmenschen zum Beweise der Theorie von der ursprünglichen Güte des menschlichen Charakters; die dem entgegengesetzte Fiktion eines in einsamer Wildnis zum Tier gewordenen Menschen bei Comenius zum Beweise der Notwendigkeit der Erziehung; die Condillac-Bonnetsche Fiktion eines in eine Marmorhülle gekleideten Menschen zum Beweise der sensualistischen Theorie vom Ursprung aller seelischen Erscheinungen; die[S. 134] Fiktion eines einsinnigen Menschen (nur Gesichtssinn!) bei Berkeley, Lotze und Helmholtz (zu anderem Zwecke auch schon bei Th. Hobbes) zum Beweise der empiristischen Theorie der Tiefenwahrnehmung; die Fiktion einer chaotischen Fixsternregion bei John Stuart Mill zum Beweise seiner empiristischen Theorie der Kausalität; endlich die J. H. v. Thünensche Fiktion eines isolierten Staates zum Beweis der von ihm (auf Grund praktisch gewonnener Erfahrungen) begründeten „Intensitätstheorie“ des landwirtschaftlichen Betriebes (Terminus nach Richard Krzymowski, Kl. Abh., 1900, S. 10).[25] — Beispiele widerlegender Fiktionen bilden die bekannte, aus der Scholastik stammende Fabel vom Buridanschen Esel zur Widerlegung der deterministischen Theorie des Willens; sowie die Lamettriesche Fiktion eines in völligster Einsamkeit aufgewachsenen Menschen (so schon bei Arnobius, zirka 300 n. Chr. Geb.) zum Beweis der Ungültigkeit der Lehre von den angeborenen Ideen.
Den Fiktionen der zuletzt besprochenen Art logisch verwandt, aber von noch geringerer Beweiskraft als diese, sind die staatswissenschaftlichen, pädagogischen und religiös-ethischen Utopien. Diese haben zumeist den Zweck, gewisse Theorien des politischen, sozialen oder religiösen Lebens durch die Fiktion eines auf ebendiese aufgebauten Gemeinwesens zureichend zu begründen. Aus diesem Gesichtspunkte heraus sind Staatsromane wie Platons Politeia, Thomas Morus’ „Über den besten Staat oder die neue Insel Utopia“, Campanellas Sonnenstaat und ähnliche Werke von Morelly, Fourier, Cabet u. a. entstanden; aus diesem Gesichtspunkt heraus haben auch Erziehungsromane wie Xenophons Kyropädie, Fénélons Telemaque, Rousseaus Emile sowie religiös-ethische Träumereien nach der Art von Johann Valentin Andreaes Christianopolis, ebenso die utopischen Zukunftsschilderungen Auguste Comtes, Saint-Simons u. a. ihren Ursprung genommen. — Stehen die Fiktionen bereits zu einem nicht geringen Teil hart auf der Grenze der Wissenschaft, so haben wir mit den Utopien diese schon überschritten und das breite Zwischenland betreten, das sich von der Wissenschaft zur Kunst hin dehnt.
Das logische Problem der Fiktion und Utopie ist in den letzten Jahren besonders zur Erörterung gelangt durch das Erscheinen von Hans Vaihingers umfangreichem Jugendwerk: „Die Philosophie des Als-Ob“ (2. Aufl., Berlin[S. 135] 1913), das eine in vieler Hinsicht sehr anregende, jedoch nach keiner Richtung hin abschließende Untersuchung über die „theoretischen, praktischen und religiösen Fiktionen der Menschheit“ enthält. Der Grundfehler des Vaihingerschen Werkes liegt in der mangelhaften begrifflichen Scheidung zwischen den Fiktionen im eigentlichen Sinne und gewissen damit verwandten methodischen Faktoren des wissenschaftlichen Denkens. Weder wissenschaftliche Abstraktionen (wie der Begriff des leeren Raumes, des Bewußtseins überhaupt) noch hypothetische Erklärungsversuche (wie die Annahme von Atomen, Molekülen, Elektronen, Ionen, Kräften, des Äthers, der Gedächtnisspuren usw.) sind den Fiktionen zuzurechen; denn bei den ersteren fehlt entweder die Annahme, daß dem auf sie gerichteten Existentialurteile Gültigkeit zukomme, gänzlich (so beim „Bewußtsein überhaupt“); oder aber, wo diese nicht fehlt (wie beim Begriff des leeren Raumes), ist doch zum mindesten das Bewußtsein der tatsächlichen Ungültigkeit jenes Existentialurteils keinesfalls vorhanden. Bei den letzteren fällt ferner ebendieses Bewußtsein tatsächlicher Ungültigkeit durchgängig aus, wie wir denn Kräfte, Atome und Moleküle, Gedächtnisresiduen und ähnliches zur Erklärung der physikalisch-chemischen und psychologischen Erscheinungen nicht nur zum Schein annehmen, sondern vielmehr als wirklich vorhanden postulieren.
[21] Der Universalienstreit des Mittelalters drehte sich, roh gesagt, um die Frage, ob die Allgemeinbegriffe (Universalia) als selbständige Wesenheiten (Platons und Plotins Ideen) vor den Dingen (ante res) seien oder aber dadurch, daß sie in den erkennenden Geistern gebildet würden, erst nach den Dingen (post res) kämen.
[22] „Ich weiß nicht, ich werde nicht wissen“; nach dem bekannten Vortrag Dubois-Reymonds.
[23] Vgl. dazu die schon früher erwähnte Darstellung von Oswald Külpe (ANuG Bd. 146).
[24] Analoges gilt für die ergänzende Induktion.
[25] Zum letzteren vergleiche auch Max Büchler, Joh. Heinr. v. Thünen und seine nationalökonomischen Hauptlehren, Bern 1907, S. 16 ff.
(Die für das Studium unentbehrlichen Hauptwerke sind durch ein Sternchen hinter dem Verfassernamen kenntlich gemacht.)
Carl Prantl*, Geschichte der Logik im Abendlande, 4 Bde., 1855-1870 (bis zum Ausgang des Mittelalters reichend).
Friedrich Ueberweg, System der Logik und Geschichte der logischen Lehren, 5. Aufl. von J. B. Meyer, Bonn 1882.
Friedrich Harms, Die Philosophie in ihrer Geschichte, Teil II: Geschichte der Logik, Berlin 1878 (mit Vorsicht zu benutzen).
Benno Erdmann*, Logik, Bd. I: Logische Elementarlehre, 2. Aufl, Halle 1907.
Christoph Sigwart*, Logik, 2 Bde., 4. Aufl. herausg. von Heinrich Maier, Tübingen 1911.
Wilhelm Wundt*, Logik, 3 Bde., 3. Aufl., Stuttgart 1906-1908.
Hermann Lotze, System der Philosophie, Teil I: Logik, 2. Aufl. Leipzig 1880 (neu herausgegeben in der Philosophischen Bibliothek [Bd. 141] von Georg Misch, Leipzig 1912).
Wertvoll zu Studienzwecken sind von Werken geringeren Umfanges, zum Teil solchen älteren Ursprungs, auch:
[S. 136]
Moritz Wilhelm Drobisch, Neue Darstellung der Logik, 4. Aufl., Leipzig 1875.
Alois Höfler, Grundlehren der Logik und Psychologie, 2. Aufl., 1906.
William Stanley Jevons, Leitfaden der Logik, deutsch von Hans Kleinpeter, Leipzig 1906.
August Stadler, Logik, Leipzig 1912.
Ferner das oben genannte System der Logik von Friedrich Ueberweg.
Vom katholischen Standpunkt aus haben u. a. die Logik behandelt:
Georg Hagemann, Logik und Noetik, 9. und 10. Aufl., bearb. v. Ad. Dyroff, Freiburg i. Br. 1915.
Joseph Geyser, Grundlagen der Logik und Erkenntnistheorie, Münster 1909.
B. W. Switalski, Vom Denken und Erkennen, Kempten 1914.
Spezielle Richtungen vertreten:
Theodor Lipps, Grundzüge der Logik, Hamburg 1893.
Wilhelm Schuppe, Erkenntnistheoretische Logik, Bonn 1878.
— Grundriß der Erkenntnistheorie und Logik, 2. Aufl., Berlin 1910.
Hermann Cohen, Logik der reinen Erkenntnis, Berlin 1902.
Ferner: Paul Natorp in mehreren Schriften.
Das deutsche Hauptwerk der mathematischen Logik ist:
Ernst Schröder, Vorlesungen über die Algebra der Logik, 3 Bde., Leipzig 1890-1895.
Kurze orientierende Darstellungen dieser Richtung bei:
Ernst Schröder, Abriß der Algebra der Logik, Teil I, herausg. v. Eugen Müller, Leipzig 1909.
Joseph Hontheim, Der logische Algorithmus, Berlin 1895.
Heinrich Maier*, Die Syllogistik des Aristoteles, 2 Teile in 3 Bänden. Tübingen 1896-1900.
Adolf Trendelenburg, Geschichte der Kategorienlehre, in: Hist. Beitr. z. Philos. Bd. I, Berlin 1846.
Richard Herbertz, Studien zum Methodenproblem und seiner Geschichte, Köln 1910.
Ferner: A. Riehl, Die englische Logik der Gegenwart; in: Viert. f. wiss. Philos., Bd. I, 1877.
L. Liard, Die neuere englische Logik, deutsch von J. Imelmann, 2. Aufl., Leipzig 1883.
Edmund Husserl*, Logische Untersuchungen, 2 Bde., 2. Aufl., Halle 1913.
Alois Riehl, Logik und Erkenntnistheorie, in: Die Kultur der Gegenwart, herausg. v. P. Hinneberg, Teil I, Abteilung 6, Berlin und Leipzig 1908.
Heinrich Maier, Logik und Erkenntnistheorie, in: Philos. Abhandlungen, Chr. Sigwart gewidmet, Tübingen 1900.
— Logik und Psychologie, in: Festschrift für Al. Riehl z. s. 70. Geb., Halle 1914.
[S. 137]
Wilhelm Windelband, Logik, in: Die Philosophie im Beginn des 20. Jahrh. Festschrift f. Kuno Fischer, 2. Aufl., Heidelberg 1907.
Ferner: Beiträge in der „Encyklopädie der philos. Wissensch.“ (herausg. v. Arnold Ruge, Bd. I, Tübingen 1912) von Wilh. Windelband, Josiah Royce, Louis Couturat, Benedetto Croce u. a.
Lehrreich auch noch:
Adolf Trendelenburg, Logische Untersuchungen, 3. Aufl., 2 Bde., Leipzig 1870 (verteidigt die metaphysische Logik gegen die formale).
B. Erdmann, Logische Studien, in: Viert. s. wiss. Philos., Bd. VI, 1882, Bd. VII, 1883.
— Zur Theorie des Syllogismus und der Induktion, in: Philos. Aufs., Ed. Zeller gew., Leipzig 1887.
Chr. Sigwart, Beiträge zur Lehre vom hypothetischen Urteile, Tübingen 1871.
— Die Impersonalien, eine logische Untersuchung, Freiburg 1888.
Alois Riehl, Beiträge zur Logik, 2. Aufl., Leipzig 1912.
Wilhelm Windelband, Beiträge zur Lehre vom negativen Urteil, in: Straßburger Abhandl. zur Philos., Ed. Zeller gew., Leipzig 1884.
— Vom System der Kategorien, in: Philos. Abhandlungen, Chr. Sigwart gew., Tübingen 1900.
Hans Cornelius, Versuch einer Theorie der Existentialurteile, München 1894.
Adolf Dyroff, Über den Existentialbegriff, Freiburg 1902.
Fritz Medicus, Bemerkungen zum Problem der Existenz mathematischer Gegenstände, in: Festschrift der Kantstudien zum 70. Geb. Al. Riehls, Berlin 1914.
Joh. Ed. Th. Wildschrey, Die Grundlagen einer vollständigen Syllogistik, Halle 1907.
Ferner: Friedrich Albert Lange, Logische Studien, Iserlohn 1877.
A. Marty, Über subjektlose Sätze, in: Viert. f. wiss. Philos. Bd. 8, 1884; Bd. 18, 1894.
John Stuart Mill*, System der deduktiven und induktiven Logik, 3 Bde., deutsch in: Ges. Werke, herausg. v. Theod. Gompertz, Bd. 2-4, Leipzig 1872-1873.
Richard Hönigswald, Beiträge zur Erkenntnistheorie und Methodenlehre, Leipzig 1906.
Bruno Bauch, Studien zur Philosophie der exakten Wissenschaften, Heidelberg 1911.
Johannes von Kries, Logik, Tübingen 1916.
Ferner: B. Erdmann, Theorie der Typen-Einteilungen, in: Philos. Monatshefte, Bd. 30, Berlin 1884.
— Methodologische Konsequenzen aus der Theorie der Abstraktion (Abh. d. Kgl. Pr. Akad. d. Wiss.), Berlin 1916.
[S. 138]
Heinrich Rickert, Zur Lehre von der Definition, 2. Aufl., Tübingen 1915.
Zur Einführung in die zahlreichen methodologischen Probleme des mathematischen Denkens vergleiche man: B. Erdmann, Die Axiome der Geometrie, Leipzig 1877; O. Hölder, Anschauung und Denken in der Geometrie, Leipzig 1900; Jonas Cohn, Voraussetzungen und Ziele des Erkennens, Leipzig 1908, Teil II; Richard Hönigswald, Zum Streit über die Grundlagen der Mathematik, Heidelberg 1912; A. Voß, Über das Wesen der Mathematik, Leipzig 1913; sowie die dort angeführte Literatur.
Zur neueren Logik der Geschichtswissenschaft: Wilh. Windelband, Naturwissenschaft und Geschichte, 2. Aufl., Straßburg 1900 (auch in: Präludien Bd. II, Tübingen 1915); Ed. Meyer, Zur Theorie und Methodik der Geschichte, Halle 1902; Heinrich Rickert, Die Grenzen der naturwissenschaftlichen Begriffsbildung, Tübingen 1902; Über die Aufgaben einer Logik der Geschichte, Archiv f. syst. Phil., Bd. 8, 1902; Kulturwissenschaft und Naturwissenschaft, 2. Aufl., Tübingen 1910; Geschichtsphilosophie, in: Die Philosophie im Beginn des 20. Jahrh., Festschr. f. Kuno Fischer, 2. Aufl., Heidelberg 1907; ferner: Eduard Spranger, Die Grundlagen der Geschichtswissenschaft, Berlin 1905; Kurt Sternberg, Zur Logik der Geschichtswissenschaft, Philos. Vortr. Nr. 7, Berlin 1914; Heinrich Maier, Das geschichtliche Erkennen, Göttingen 1914; sowie einzelne Schriften von Ernst Bernheim.
Zur Frage nach der systematischen Gliederung der Wissenschaften: Wilh. Wundt, Über die Einteilung der Wissenschaften, in Philos. Studien, Bd. 5, Leipzig 1888; B. Erdmann, Die Gliederung der Wissenschaften, in: Viert. f. wiss. Philos., Bd. 2, Leipzig 1878; Alfred Hettner, Das System der Wissenschaften, in: Preuß. Jahrbücher, Bd. 122, Berlin 1905; Carl Stumpf, Zur Einteilung der Wissenschaften, Berlin 1906; Richard Hönigswald, Vom allgemeinen System der Wissenschaften, in: Philos. Wochenschr., Bd. 4, Leipzig 1906; Zur Wissenschaftstheorie und -systematik, in Kant-Studien, Bd. 17, Berlin 1912.
(Aufgenommen sind lediglich die wichtigsten logischen Begriffe nach ihren Hauptstellen. Die Zahlen bezeichnen die Seiten.)
Die Sammlung
„Aus Natur und Geisteswelt“
nunmehr schon über 600 Bändchen umfassend, sucht seit ihrem Entstehen dem Gedanken zu dienen, der heute in das Wort: „Freie Bahn dem Tüchtigen!“ geprägt ist. Sie will die Errungenschaften von Wissenschaft, Kunst und Technik einem jeden zugänglich machen, ihn dabei zugleich unmittelbar im Beruf fördern, den Gesichtskreis erweiternd, die Einsicht in die Bedingungen der Berufsarbeit vertiefend.
Sie bietet wirkliche „Einführungen“ in die Hauptwissensgebiete für den Unterricht oder Selbstunterricht des Laien, wie sie den heutigen methodischen Anforderungen entsprechen. So erfüllt sie ein Bedürfnis, dem Skizzen, die den Charakter von „Auszügen“ aus großen Lehrbüchern tragen, nie entsprechen können, denn solche setzen vielmehr eine Vertrautheit mit dem Stoffe schon voraus.
Sie bietet aber auch dem Fachmann eine rasche zuverlässige Übersicht über die sich heute von Tag zu Tag weitenden Gebiete des geistigen Lebens in weitestem Umfang und vermag so vor allem auch dem immer stärker werdenden Bedürfnis des Forschers zu dienen, sich auf den Nachbargebieten auf dem laufenden zu erhalten.
In den Dienst dieser Aufgabe haben sich darum auch in dankenswerter Weise von Anfang an die besten Namen gestellt, gern die Gelegenheit benutzend, sich an weiteste Kreise zu wenden, an ihrem Teil bestrebt, der Gefahr der „Spezialisierung“ unserer Kultur entgegenzuarbeiten.
So konnte der Sammlung auch der Erfolg nicht fehlen. Mehr als die Hälfte der Bändchen liegen, bei jeder Auflage durchaus neu bearbeitet, bereits in 2. bis 6. Auflage vor, insgesamt hat die Sammlung bis jetzt eine Verbreitung von weit über 4 Millionen Exemplaren gefunden.
Alles in allem sind die schmucken, gehaltvollen Bände besonders geeignet, die Freude am Buche zu wecken und daran zu gewöhnen, einen kleinen Betrag, den man für Erfüllung körperlicher Bedürfnisse nicht anzusehen pflegt, auch für die Befriedigung geistiger anzuwenden. Durch den billigen Preis ermöglichen sie es tatsächlich jedem, auch dem wenig Begüterten, sich eine Bücherei zu schaffen, die das für ihn Wertvollste „Aus Natur und Geisteswelt“ vereinigt.
Jedes der meist reich illustrierten Bändchen
ist in sich abgeschlossen und einzeln käuflich
Jedes Bändchen geheftet M. 1.20, gebunden M. 1.50
Teuerungszuschläge 30% einschließl. 10% Zuschlag der
Buchhandlung
Leipzig, im Juni 1918. B. G. Teubner
Jedes Bändchen geheftet M. 1.20, gebunden M. 1.50
Bisher sind zur Philosophie und Psychologie erschienen:
Einführung in die Philosophie. Von Professor Dr. R. Richter. 4. Auflage von Privatdozent Dr. M. Brahn. (Bd. 155.)
Die Philosophie. Einführung in die Wissenschaft, ihr Wesen u. ihre Probleme. Von Oberrealschuldirektor H. Richert. 3. Aufl. (Bd. 186.)
Philosophisches Wörterbuch. Von Oberlehrer Dr. Paul Thormeyer. 2. Aufl. (Bd. 520.)
Grundriß der Logik. Von Dr. K. J. Grau. (Bd. 637.)
Einführung in die Psychologie. Von Prof. Dr. E. von Aster. Mit 4 Abbildungen. (Bd. 492.)
Einführung in die experimentelle Psychologie. Von Prof. Dr. N. Braunshausen. Mit 17 Abbildungen im Text. (Bd. 484.)
* Die Ergebnisse der angewandten Psychologie. Von Prof. Dr. G. Anschütz. (Bd. 678.)
Die Seele des Menschen. Von Geh. Rat Professor Dr. J. Rehmke. 4. Auflage. (Bd. 36.)
Die Mechanik des Geisteslebens. Von Geh. Med.-Rat Dir. Prof. Dr. M. Verworn. 4. Auflage. Mit Figuren. (Bd. 200.)
Psychologie des Kindes. Von Professor Dr. R. Gaupp. 4. Auflage. Mit 17 Abbildungen. (Bd. 213/14.)
Geistige Veranlagung und Vererbung. Von Dr. med. et phil. Georg Sommer. (Bd. 512.)
Handschriftenbeurteilung. Eine Einführung in die Psychologie der Handschrift. Von Prof. Dr. G. Schneidemühl. 2. Aufl. Mit 51 Handschriftennachbildungen im Text und 1 Tafel. (Bd. 514.)
Hypnotismus und Suggestion. Von Dr. E. Trömner. 3. Auflage. (Bd. 199.)
Die Psychologie des Verbrechers. Kriminalpsychologie. Von Kgl. Strafanstaltsdirektor Dr. med. P. Pollitz. 2. Auflage. Mit 5 Diagrammen. (Bd. 248.)
Grundzüge der Ethik. Mit besonderer Berücksichtigung der pädagogischen Probleme. Von E. Wentscher. (Bd. 397.)
Aufgaben und Ziele des Menschenlebens. Von Professor Dr. J. Unold. 4. Auflage. (Bd. 12.)
Sittl. Lebensanschauung. d. Gegenw. V. weil. Geh. Kirchenr. Prof. Dr. O. Kirn. 3. A., durchges. v. Prof. Dr. O. H. Stephan. (Bd. 177.)
Das Problem der Willensfreiheit. Von Professor Dr. G. F. Lipps. (Bd. 383.)
Sexualethik. Von Prof. Dr. H. E. Timerding. (Bd. 592).
* Einführung in die Geschichte der Ästhetik. Von Dr. H. Nohl. (Bd. 602.)
Ästhetik. Von Professor Dr. R. Hamann. 2. Aufl. (Bd. 345.)
Poetik. Von Dr. R. Müller-Freienfels. (Bd. 460.)
Die moderne Naturphilosophie. Von Privatdoz. Dr. J. M. Verweyen. (Bd. 491.)
Entstehung der Welt und der Erde nach Sage und Wissenschaft. Von weil. Geh. Reg.-Rat Prof. Dr. M. B. Weinstein. 2. Aufl. (Bd. 223.)
Untergang der Welt und der Erde nach Sage und Wissenschaft. Von weil. Geh. Reg.-Rat Professor Dr. M. B. Weinstein. (Bd. 470.)
Sternglaube und Sterndeutung. Die Geschichte und das Wesen der Astrologie. Unter Mitwirkung von Prof. Dr. C. Bezold dargestellt von Geh. Hofrat Prof. Dr. Fr. Boll. Mit einer Sternkarte und 20 Abb. (Bd. 638.)
Führende Denker. Geschichtliche Einleitung in die Philosophie. Von Prof. Dr. J. Cohn. 3. Aufl. Mit 6 Bildnissen. (Bd. 176.)
Die Freimaurerei. Einführung in ihre Anschauungswelt und ihre Geschichte. Von weil. Geh. Rat Dr. L. Keller. 2. Aufl. von Geh. Archivrat Dr. G. Schuster. (Bd. 463.)
Griechische Weltanschauung. Von Professor Dr. M. Wundt. 2. Aufl. (Bd. 329.)
* Religion und Philosophie im alten Orient. Von Prof. Dr. E. v. Aster. (Bd. 521.)
Die Weltanschauungen der großen Philosophen der Neuzeit. Von weil. Professor Dr. L. Busse. 6. Auflage. herausgeg. von Geh. Hofrat Professor Dr. R. Falckenberg. (Bd. 56.)
Die großen englischen Philosophen Locke, Berkeley, Hume. Von Oberlehrer Dr. P. Thormeyer. (Bd. 481.)
Rousseau. Von Professor Dr. P. Hensel. 2. Auflage. Mit 1 Bildnis. (Bd. 180.)
Immanuel Kant. Darstellung und Würdigung. Von weil. Professor Dr. O. Külpe. 4. Auflage, hrsg. von Professor Dr. A. Messer. Mit 1 Bildnis Kants. (Bd. 146.)
Schopenhauer. Seine Persönlichkeit, seine Lehre, seine Bedeutung. Von Oberrealschuldirektor H. Richert. 3. Auflage. Mit 1 Bildnis. (Bd. 81.)
Herbarts Lehren und Leben. Von weil. Pastor O. Flügel. 2. Auflage. Mit 1 Bildnis Herbarts. (Bd. 164.)
Herbert Spencer. Von Dr. K. Schwarze. Mit 1 Bildnis. (Bd. 245.)
Die Philosophie der Gegenwart in Deutschland. Eine Charakteristik ihrer Hauptrichtungen. Von weil. Prof. Dr. O. Külpe. 6. Auflage. (Bd. 41.)
Henri Bergson, der Philosoph moderner Religion. Von Pfarrer Dr. E. Ott. (Bd. 480.)
Die mit * bezeichneten und weitere Bände befinden sich in Vorbereitung.
Kurzer Abriß der Logik u. Psychologie für höhere Lehranstalten. Von Prof. Dr. Oskar Weise. 2. Aufl. Steif geh.
M. —.50
„Das Büchlein, dem in einer Zeit, die sich der Wichtigkeit der philosophischen Propädeutik allmählich wieder bewußt wird, eine besondere symptomatische Bedeutung zukommt, hat vor allem zwei Vorzüge.
Einmal ist es außerordentlich übersichtlich, ein bei logischen Definitionen wie Begriff, Urteil, Schluß oder psychologischen Erörterungen wie Erkennen, Fühlen, Wollen außerordentlich wichtiger Faktor. Sodann knüpfen die vortrefflichen Beispiele an das Naheliegende, Bekannte an, um von da zur Regel überzuleiten. Da die Arbeit den neueren Forschungen der Psychologie angepaßt ist, kann sie warm empfohlen werden.“
(Zeitschr. f. lateinl. höh. Schulen.)
Geschichte der Psychologie. Von Prof. Dr. Otto Klemm. Geb.
M. 8.—
Grundlagen der Psychologie. Von Prof. Dr. Th. Ziehen. In 2 Bänden. Buch I: Erkenntnistheoretische Grundlegung der Psychologie. Buch II: Prinzipielle Grundlegung der Psychologie. Geh. je M. 4.40, geb.
je M. 5.—
Über Vererbung psychischer Fähigkeiten. Von Prof. Dr. W. Peters. Geh.
M. 6.50
Der Wille. Versuch einer psychologischen Analyse. Von E. Wentscher. Geh. M. 2.40, geb.
M. 2.80
Experimentelle praktische Schülerkunde. Von Marx Lobsien. Mit einem Beitrag über das pathologische Kind von Direktor Dr. O. Mönkemöller. Mit 16 Figuren im Text und 1 Tafel.
Geh. M. 4.—, geb.M. 5.—
Jugendpsychologie. Von Lyzeallehrer W. Peper. Mit Abbildungen. 2. Auflage. Geb.
M. 1.80
Hierzu erschienen Quellenhefte von demselben:
1. Beobachtungen u. Untersuchungen a. d. Jugendpsychologie. Geh.
M. —.80
2. Junge Seelen. Bilder zur Jugendpsychologie aus Kinderstube, Biographie und Dichtung. 2. Auflage. Geh.
M. —.90
3. Darstellungen aus der neueren Psychologie u. Pädagogik. Geh.
M. —.80
Grundzüge der Psychologie und Logik. Von Lyzeallehrer W. Peper. 1. Hälfte. Geb.
M. 1.60
Psychologie der Sprachpädagogik. Versuche zu einer Darstellung der Prinzipien des fremdsprachlichen Unterrichts auf Grund der psychologischen Natur der Sprache von Chr. B. Flagstad, Adjunkt a. der Kgl. Metropolitanschule in Kopenhagen. Vom Verfasser aus dem Dänischen übersetzt. Geh. M. 5.—, geb.
M. 6.—
Psychologie der Kunst. Eine Darstellung ihrer Grundzüge. Von Dr. R. Müller-Freienfels. In 2 Bdn. Band I: Die Psychologie des Kunstgenießens und des Kunstschaffens. Band II: Die Formen des Kunstwerks und die Psychologie der Wertung. Geh. je M. 4.40, in 1 Band geb.
M. 10.—
Der weibliche Typus als Problem der Psychologie und Pädagogik. Ein Beitrag zur künftigen Nationalerziehung. Von Dr. K. Haase. Steif geh.
M. 2.—
Teuerungszuschlag auf sämtl. Preise (einschl. des Zuschl. der Buchhandl.) 30%
Verlag von B. G. Teubner in Leipzig und Berlin
Philosophische Propädeutik
Hrsg. von Geh. Reg.-Rat u. Oberreg.-Rat Dr. G. Lambeck. Geb. ca. M. 5.—
Inhalt: Vorwort. – Die Philosophie u. d. Einzelwissenschaften. V. Hrsgeber. – Dir. Prof. Dr. Goldbeck: Mathematik. Physik. – Prof. Dr. Gruner: Biologie. – Prof. Dr. O. Hoffmann: Die Sprache. – Geh. u. Ob.-Reg.-Rat Lambeck: Geschichte. – Gymnas.-Dir. Dr. Lorentz: Dtsche. Literatur. – Oberlehrer Dr. Hoffmann: Die Antike. – Prof. Dr. Messer: Zusammenfassung. – Register.
Auf neuem Wege will das Buch der philosophischen Propädeutik in unseren höheren Lehranstalten wieder eine feste Stellung gewinnen. In der Überzeugung, daß es in erster Linie darauf ankommt, im Schüler den Sinn für philosophische Fragestellung und Betrachtung zu wecken, sucht es aus den einzelnen Unterrichtsfächern heraus die philosophischen Probleme zu entwickeln, zu denen ein im wissenschaftlichen Geiste erteilter mathematischer, physikalischer und biologischer, deutscher, geschichtlicher und altsprachlicher Unterricht notwendiger- und natürlicherweise hinführen muß. Ein weiterer Abschnitt erörtert die mit der Entwicklung der Sprache als solcher zusammenhängenden Fragen. Ein systematischer Teil faßt das in den einzelnen Fächern Gebotene zusammen, ergänzt es soweit, daß die verschiedenen Fragen in einem gewissen Zusammenhange erscheinen u. gibt einen Überblick über die wichtigsten psychologischen Vorgänge.
Philosophisches Lesebuch
Von Professor Dr. Bastian Schmid. Zum Gebrauch an höheren Schulen und zum Selbststudium. Gebunden M. 2.60
„... Dem Zwecke, zur Kritik zu erziehen, dient in trefflicher Weise die Gegenüberstellung von Aufsätzen wie Mettries ‚Der Mensch eine Maschine,‘ Häckels ‚Die Seele‘ und Du Bois-Reymonds ‚Über die Grenzen des Naturerkennens‘. Eine Art historische Einleitung gibt ein Abschnitt aus Riehls ‚Wesen und Entwicklung der Philosophie‘; zur Verbindung der einzelnen Gedankenreihen dienen kürzere Kapitel des Verfassers. Besonders nützlich dürften die Aufsätze zur Ethik und Ästhetik sein.“
(Blätter f. das bayerische Gymnasialschulwesen.)
Zur Einführung in die Philosophie der Gegenwart
Von Geheimrat Prof. Dr. A. Riehl. 4. Aufl. Geh. M. 3.—, geb. M. 3.60
„Von den üblichen Einleitungen in die Philosophie unterscheidet sich Riehls Buch nicht bloß durch die Form der freien Rede, sondern auch durch seine ganze methodische Auffassung und Anlage. Nichts von eigenem System, nichts von langatmigen, logischen, psycholog. oder gelehrten historischen Entwicklungen, sondern eine lebendig anregende, in das Zentrum der Philosophie führende Betrachtungsweise.“
(Monatsschrift für höhere Schulen.)
Einleitung in die Philosophie
Von Prof. Dr. Hans Cornelius. 2. Aufl. Geh. M. 5.20, geb. M. 6.—
„Die gegebenen Gesichtspunkte und Einleitungen führen tief in die Erkenntnistheorie und Psychologie. Verf. sucht zu einem eigenen Standpunkt zu führen, Einsicht in die rein empirische Bedeutung und in den Mechanismus aller Naturerklärung zu geben. Leser, die einer tiefgründigen Untersuchung nicht aus dem Wege gehen, werden viel von ihm lernen.“
(Leipz. Ztg.)
Weltanschauung und modernes Bildungsideal
Von Professor Dr. G. F. Lipps. Geheftet M. 4.—, gebunden M. 5.—
„Das Buch ist interessant und fesselnd geschrieben. Wir können eine eingehende Beschäftigung mit ihm nur empfehlen. Niemals langweilig und trocken, bietet es eine Fülle von Anregungen, aus denen jeder schöpfen kann, der mitarbeiten will an der Ausbildung eines Bildungsideals der Zukunft.“
(Zeitschrift für pädagogische Psychologie.)
Hauptprobleme der Ethik
9 Vortrage v. Prof. Dr. P. Hensel. 2., erw. Aufl. M. 1.80, geb. M. 2.40
„Dieses schlicht und allgemeinverständlich geschriebene Buch darf auf das Lob, nicht nur Philosophie, sondern auch philosophieren zu lehren, Anspruch erheben. Dieses Lob ist eins der schönsten für eine philosophische Schrift. Das Buch läßt überall ein glückliches und energisches Denken spüren, das zum Selbstdenken anregt.“
(Zeitschrift f. päd. Psychol.)
Verlag von B. G. Teubner in Leipzig und Berlin
Allgem. Geschichte der Philosophie
(Die Kultur der Gegenwart, hrsg. von Prof.
P. Hinneberg. Teil I, Abt. V.)
2., verm. u. verb. Aufl. Geh. M. 14.—, geb. M. 16.—, in Halbfranz M. 18.—
Inhalt: Einleitung. Die Anfänge der Philosophie und die Philosophie der primitiven Völker: W. Wundt. A. Die orientalische (ostasiatische) Philosophie. I. Die indische Philosophie: H. Oldenberg. II. Die chinesische Philosophie: W. Grube. III. Die japanische Philosophie: T. Inouye. B. Die europäische Philosophie (und die islam.-jüd. Philosophie des Mittelalters). I. Die europäische Philosophie des Altertums: H. v. Arnim. II. Die patristische Philosophie: Cl. Baeumker. III. Die islamische und die jüdische Philosophie: J. Goldziher. IV. Die christliche Philosophie des Mittelalters: Cl. Baeumker. V. Die neuere Philosophie: W. Windelband.
Systematische Philosophie
(Die Kultur der Gegenwart, hrsg. von Prof. P. Hinneberg. Teil I,
Abt. VI.)
2. Aufl. Geheftet M. 10.—, gebunden M. 12.—, in Halbfranz M. 14.—
Inhalt: Allgemeines. Das Wesen der Philosophie: W. Dilthey. Die einzelnen Teilgebiete. I. Logik und Erkenntnistheorie: A. Riehl. II. Metaphysik: W. Wundt. III. Naturphilosophie: W. Ostwald. IV. Psychologie: H. Ebbinghaus. V. Philosophie der Geschichte: R. Eucken. VI. Ethik: Fr. Paulsen. VII. Pädagogik: W. Münch. VIII. Ästhetik: Th. Lipps. — Die Zukunftsaufgaben der Philosophie: Fr. Paulsen.
Das Grundproblem Kants
Eine kritische Untersuchung und Einführung in die
Kant-Philosophie.
Von Prof. Dr. A.
Brunswig. Geheftet M. 3.60, gebunden M. 4.20
Das Buch betrachtet als Grundproblem Kants die zentrale Frage der Kritik der reinen Vernunft nach der Möglichkeit eines allgemeingültigen, notwendigen Wissens. Es kann vermöge der zentralen Stellung seines Gegenstandes zugleich als Einführung in das Studium der Kantschen Philosophie und ihrer modernen Kritik, ja der Erkenntnistheorie und der Philosophie überhaupt dienen.
Die philosophischen Grundlagen der Wissenschaften
Vorlesungen gehalten an der Universität Berlin von Professor Dr. B. Weinstein. Gebunden M. 9.—
„W. versteht es meisterhaft, auch einen spröden Gegenstand schmackhaft zu machen. Dies liegt in seiner gegenständlichen Redeweise, die zum Hörer hinabzusteigen scheint, während sie ihn unmerklich auf die Höhe führt. Das Buch ist warm zu empfehlen.“
(Der Tag.)
Naturphilosophie
Unt. Redaktion v. Geh. Reg.-Rat Prof. Dr. C. Stumpf. Bearb. von Prof. Dr. E. Becher. (Die Kultur der Gegenwart. Hrsg. von Prof. P. Hinneberg. Teil III. Abt. VII, 1.) Geh. M. 14.—, gebunden M. 16.—, in Halbfr. M. 18.—
Einleitung. Aufgabe der Naturphilosophie. Naturerkenntnistheorie. Gesamtbild der Natur.
„Eine ungewöhnlich umfassende und eindringende Kenntnis aller Naturwissenschaften liegt dem Werke offenbar zugrunde. Bemerkenswert ist die Fähigkeit des Verfassers zu anschaulicher und gemeinverständlicher Darstellung; fast mühelos gelingt es ihm, auch sehr abstrakte und schwierige Theorien elementar und durchsichtig zu entwickeln, ohne dabei auf wissenschaftliche Genauigkeit zu verzichten. Die gründliche naturwissenschaftliche Schulung zeigt sich auch in der methodischen Art, wie der Verfasser seinen Gegenstand behandelt.“
(Literarisches Zentralblatt für Deutschland.)
Himmelsbild und Weltanschauung
im Wandel der Zeiten. Von Prof. Troels-Lund. Autorisierte, vom Verfasser durchgesehene Übersetzung von L. Bloch. 4. Aufl. Geb. M. 5.—
„... Es ist eine Lust, diesem kundigen und geistreichen Führer auf dem langen, nie ermüdenden Wege durch Asien, Afrika und Europa, durch Altertum und Mittelalter bis herab in die Neuzeit zu folgen. Es ist ein Werk aus einem Guß, in großen Zügen und ohne alle Kleinlichkeit geschrieben.“
(W. Nestle i. d. Neuen Jahrb. f. d. klass. Altertum.)
Verlag von B. G. Teubner in Leipzig und Berlin
WISSENSCHAFT UND HYPOTHESE
Sammlung von Einzeldarstellungen aus dem Gesamtgebiete der Wissenschaften mit bes. Berücksichtigung ihrer Grundlagen u. Methoden, ihrer Endziele u. Anwendungen
Die Sammlung will die in den verschiedenen Wissensgebieten durch rastlose Arbeit gewonnenen Erkenntnisse von umfassenden Gesichtspunkten aus im Zusammenhang miteinander betrachten. Die Wissenschaften werden in dem Bewußtsein ihres festen Besitzes in ihren Voraussetzungen dargestellt, ihr pulsierendes Leben, ihr Haben, Können und Wollen aufgedeckt. Andererseits aber wird in erster Linie auch auf die durch die Schranken der Sinneswahrnehmung und der Erfahrung überhaupt bedingten Hypothesen hingewiesen.
I. Wissenschaft und Hypothese. Von † Henri Poincaré. Deutsch von L. und F. Lindemann. 3. Aufl.
Geb. M. 4.80
II. Der Wert der Wissenschaft. Von † Henri Poincaré. Deutsch von E. u. H. Weber. Mit einem Bildnis. 2. Aufl.
Geb. M. 3.60
III. Mythenbildung u. Erkenntnis. Eine Abhandlung über die Grundlagen der Philosophie. Von G. F. Lipps.
Geb. M. 5.—
IV. Die nichteuklidische Geometrie. Historisch-kritische Darstellung ihrer Entwicklung. Von R. Bonola. Deutsch von H. Liebmann.
Geb. M. 5.—
V. Ebbe und Flut sowie verwandte Erscheinungen im Sonnensystem. Von G. H. Darwin. Deutsch von A. Pockels. 2. Aufl. Mit 52 Abb. Geb.
M. 8.—
VI. Das Prinzip der Erhaltung der Energie. Von M. Planck. 3. Aufl. Geb.
M. 6.—
VII. Grundlagen der Geometrie. Von D. Hilbert. 4. Aufl.
Geb. M. 6.—
VIII. Geschichte der Psychologie. Von O. Klemm.
Geb. M. 8.—
IX. Erkenntnistheoret. Grundzüge der Naturwissenschaften u. ihre Beziehungen zum Geistesleben der Gegenwart. Von P. Volkmann. 2. Aufl.
Geb. M. 6.—
X. Wissenschaft und Religion in der Philosophie unserer Zeit. Von É. Boutroux. Deutsch von E. Weber. Mit Einführungswort v. H. Holtzmann.
Geb. M. 6.—
XI. Probleme der Wissenschaft. Von E. Enriques. Deutsch von K. Grelling. 2 Teile. I. Wirklichkeit und Logik. Geb. M. 4.—. II. Die Grundbegriffe der Wissenschaft.
Geb. M. 5.—
XII. Die logischen Grundlagen der exakten Wissenschaften. Von P. Natorp.
Geb. M. 6.60
XIII. Pflanzengeographische Wandlungen der deutschen Landschaft. V. H. Hausrath.
Geb. M. 5.—
XIV. Das Weltproblem vom Standpunkte des relativistischen Positivismus aus. Von J. Petzold. 2. Aufl. Geb.
M. 3.—
XV. Wissenschaft und Wirklichkeit. V. M. Frischeisen-Köhler.
Geb. M. 8.—
XVI. Das Wissen der Gegenwart in Mathematik u. Naturwissenschaften. Von É. Picard. Deutsch von F. und L. Lindemann.
Geb. M. 6.—
XVII. Wissenschaft u. Methode. Von H. Poincaré. Deutsch von F. u. L. Lindemann.
Geb. M. 5.—
XVIII. Probleme der Sozialphilosophie. Von R. Michels.
Geb. M. 4.80
XIX. Ethik als Kritik der Weltgeschichte. Von A. Görland.
Geb. M. 7.50
XX. Die Grundlagen der Psychologie. Von Th. Ziehen. Teil I.
Geh. M. 4.40, geb. M. 5.—
XXI. —— Teil II.
Geh. M. 4.40, geb. M. 5.—
In Vorbereitung befinden sich:
Czuber, Die philosophischen Grundlagen der Wahrscheinlichkeitsrechnung. – K. Dove, Die Erde als Wohnsitz des Menschen. – Ph. Frank, Relativitätstheorie. – A. Hettner, Probleme der Morphologie des Festlandes. – W. Johannsen, Vererbungslehre. – R. Lehmann, Grundlagen der Pädagogik. – G. Linck, Die wichtigsten Probleme der Mineralogie und Petrographie. – O. Schlaginhaufen, Anthropologie und Rassenkunde. – O. Schlüter, Methoden der geographischen Forschung. – H. v. Seeliger, Grundfragen der Astronomie, Mechanik und Physik der Himmelskörper. – R. Süring, Meteorologische Zeit- und Streitfragen. – S. Tschulok, Deszendenzlehre. – Wien, Vorlesungen über neuere Probleme der theoretischen Physik. – A. Wocikof, Grundfragen der Klimatologie.
Ausführlicher Prospekt unentgeltlich und postfrei vom Verlag in Leipzig, Poststr. 3
Verlag von B. G. Teubner in Leipzig und Berlin