
TO WHICH ARE ADDED,
A History of the Restoration of Platonic Theology,
BY THE LATTER PLATONISTS:
And a Translation from the Greek of
PROCLUS’S THEOLOGICAL ELEMENTS.
IN TWO VOLUMES.

VOL I.
LONDON, PRINTED FOR THE AUTHOR:
And Sold by T. Payne and Son; B. White and Son; J. Robson; T. Cadell; Leigh and Co.; G. Nicol; R. Faulder; and T. and J. Egerton. 1792.
[Price Two Guineas in Boards.]
Extracts from Curiosities of Literature. Second Edition.
Printed for Murray. Page 385.
Mr. T. TAYLOR, the Platonic Philosopher and the modern Plethon, consonant to that philosophy, professes Polytheism.[1]
Page 4. of the Dissertation, Vol. I. line 8. for admitted, read omitted. Page 16. line 8. for from, read form. Page 51. Vol. I. of the Commentaries, line 16. instead of They are surely not the, &c. read For surely it cannot be said that there are, &c. Line 17. for but we, read but that we. And line 19. for is by much prior to, read is by a much greater priority.
Vol. II. page 18. line 26. for and one is, read and one part is. And line 27. for another, read the other. Page 114. line 13. for The angle, read Let the angle; and instead of is bisected, in the same line, read be bisected. Page 411. line 2. for is filled with intellect, read fills intellect. And line 3. for it also participates, read also it participates.
TO
THE SACRED
MAJESTY
OF
TRUTH.
The design of the present work is to bring us acquainted with the nature and end of Mathematics in general, and of Geometry in particular: and in the execution of this design our Author has displayed an uncommon elegance of composition, and a most valuable store of recondite learning. He is not content with every where unfolding the full, and most accurate meaning of Euclid; but he continually rises in his discourse, and leads us into the depths of the Pythagoric and Platonic philosophy. We are surprised to find an use in Geometry, which at present it is by no means suspected to afford. For who would conceive that it is the genuine passage to true theology, and the vestibule of divinity? This, indeed, is by no means the case when it is studied for lucre, and applied to mechanical purposes; for then the soul is neither elevated nor enlightened; but degraded and filled with material darkness. Hence these Commentaries are alone valuable to the liberal part of mankind, who look beyond sense for certainty; and who prefer things desirable for their own sakes, before such as minister to the necessities of life.
The translation of this work is attended with great difficulty and labour; not only from the sense of the philosopher, which is always profound, and frequently obscure, but from the great incorrectness of the Greek edition, in which, exclusive of numberless typographical errors, entire sentences, essential to the connection, are frequently omitted; and in one place two pages of the Latin translation are wanting in the original, as will be shewn in our following notes. Indeed, the Latin translation of Francis Barocius the Venetian, (Patav. 1560.) which was made from a variety of manuscripts, is inconceivably valuable; for the diagrams, so necessary to a work of this kind, but which are omitted in the Greek, are here inserted; and the version is every where faithful, and sufficiently perspicuous to those who are conversant in the ancient philosophy. Barocius justly cautions the reader not to compare his version with the printed Greek, which he observes is rather lacerated than printed; as indeed, without his translation, it is impossible for any one to read the half of this invaluable work, even though he should be as perfect in Greek as in his native tongue. If I had not, therefore, fortunately acquired this translation, which is at present very rare, I would have by no means engaged in this arduous undertaking. Barocius, indeed, gives evident proofs of his possessing the philosophical genius, by the excellence of his translation, and his preface to the reader; and it is greatly to be lamented that he did not adorn his version with explanatory notes, which this profound work frequently demands, and which he was doubtless well qualified to accomplish. This defect I have endeavoured, as far as I was able, to supply; and at the same time have been cautious neither to weary the reader by prolixity, nor by too much brevity to leave him destitute of proper information. In the distribution of the first book of this work into chapters, I have followed the order of Barocius, because it is natural and obvious; and must beg leave to solicit the reader’s indulgence for using the words partible and impartible, differently from their common signification. These words I have generally employed to express the meaning of μεριστός[2] and αμεριστος[3] in the Greek, as I do not conceive that the words divisible and indivisible always convey their full signification. I have likewise used quadrangle instead of square, and quinquangle for the word pentagon. For if τρίγωνος be rendered triangle, why should not τετραγώνος be rendered quadrangle? And, as Barocius observes, why, for a similar reason, should not πεντάγωνος and ἑξάγωνος be rendered quinquangle and sexangle; and so of the rest? Uniformity is always desirable when it can be obtained; and is no where so necessary as in scientifical disquisitions.
It is likewise necessary to inform the reader, that though I have always endeavoured to give the faithful meaning of my Author, yet I have occasionally paraphrased his sense, when most obscure, and added such elucidations of my own, as I either thought necessary to the full comprehension of his matter; or which were naturally excited by the fire and spirit of the Original. If it shall appear that I have succeeded in the execution of this work, and rendered it intelligible to the lovers of truth, I shall rejoice in my success, and consider my labours sufficiently rewarded. The applause of the multitude I am neither likely nor desirous to gain; but I am anxious to procure the approbation of the discerning few, who know that the age of philosophy is past; and who esteem the works of her ancient heroes as the most precious treasures which have escaped the ravages of time.
Time, indeed, is like a deep and rapid river; whatever is trifling and light, is precipitately borne on its surface, and what is valuable and weighty, sinks to its bottom. Hence, the superficial observer collects nothing more than the rubbish, which it is forever devolving into the abyss of oblivion; while the profound and contemplative genius explores the depths of the stream, and accounts himself happy if he can gather any of the pearl which its bottom contains. Thus the discoveries of experimental philosophy, float like straws on the surface, while the wisdom of Pythagoras and Plato lies concealed in the depths of the river. I am well aware it will be said, that the reverse of this similitude is true; that the modern philosophy is the pearl, and the ancient the stubble; and that the former will be celebrated by posterity, and increase in reputation when the latter shall scarcely be known. But let us attentively examine the truth of this assertion, and shut our ears to the unsubstantial echoes of popular applause. Is it reasonable to suppose that men of such exalted abilities, as the Pythagoric and Platonic philosophers possessed, even in the estimation of their opponents, accompanied with the greatest advantages of birth and fortune, and the most unwearied attention, have discovered nothing valuable, and have left nothing behind them, but jargon and reveries? Is it to be supposed, that in an age when philosophy was almost adored; when it was esteemed by kings, cultivated by noblemen, and even reverenced by the vulgar; when empire was relinquished for its pursuit, and every danger encountered for its possession: is it to be supposed, that nothing but delusion was the offspring of so glorious a period, and nothing but folly the reward of such generous endurance? Or shall we say, that the discovery of truth was reserved for the age of experiment; and that she is alone to be apprehended in the infinite labyrinth of particulars? That she is to be investigated with the corporeal senses, and not with the powers of intellect; and that the crucible, the alembic, and the air-pump, are the only mediums of detection? If this be the case, truth is material, and may be calcined, distilled, and rarefied, like any other corporeal substance. It is no longer eternal and immutable, but perishable and fluctuating; the phantastic subject of sensible inspection, and not the steady and real object of the permanent energies of science. Shall we call this the age of philosophy, in which talents are prostituted for sustenance, and learning submits to the impudence of wealth? Shall we say that we have strengthened the cause of philosophy, by demolishing her schools; and increased her independence, by enlarging the empire of commerce? Where shall we find the man, who is at present reverenced for the profession of teaching speculative truth, or indeed who teaches it at all? Or should we chance to meet with such an obsolete character, shall we find him supported by the profession? It is a well known fact, that men formerly lived in the highest esteem by its propagation: it is equally as notorious, that a man at present would starve by such an attempt. Dare we assert, that the reason of this difference must be ascribed to the greater liberality, and more philosophical spirit of the present age? Shall we not rather say, that the period, in which these ancient heroes lived, was the golden age of philosophy;—a period so different from the present, as to appear fabulous on the comparison? For mark the distinguishing characteristics of our inferiority. The great object of ancient philosophy, was an accurate speculation of principles and causes: but that of the modern, is a confused investigation of effects. And if pursuits participate of the nature of their subjects, and causes are more noble than effects, the ancient philosophy must undoubtedly be more elevated than the modern. Again, the object of the Pythagorean and Platonic philosophy was to make its possessors wise and virtuous; and to elevate them above the common frailties and imperfections of degraded humanity; and this end was happily accomplished in its votaries, as their lives abundantly evince: but the object of modern philosophy, is a promotion of the conveniencies and refinements of life, by enlarging the boundaries of traffic; and the Mathematical Sciences are studied solely with a view to this enlargement. The design of the ancient philosophy was to remove the causes of wonder, by contemplating effects in their causes: the grand object of the modern, is to increase admiration, by attempting to investigate causes through the infinity of particular effects. So that philosophy, as Mr. Harris justly observes, now ends where it formerly began. For either there is no such thing as science, or if its existence be admitted, it can never be obtained by experimental enquiries; as these must be liable to all the inaccuracy and imperfection of their material subjects.
In short, the philosophy of Pythagoras and Plato will be found, when impartially considered, to contain every thing which can enlighten the mind, improve the morals, and exalt the character of man. It is built on the steady basis of truth, and will survive the wreck of ages. Its foundation is deep, and its summit reaches the heavens. It is a mighty rock, which modern systems may assail, like a raging sea; but, like stormy waves, they will only be broken about its impenetrable sides. To war against wisdom is folly; for opposition in this case is the destruction of its author. The moderns may, indeed, expect, because their merit is raised by the present age, above that of the ancients, to appear as giants in the eyes of posterity; but they will only verify the elegant observation of the poet[4], that
[i]
A
DISSERTATION
ON THE
PLATONIC DOCTRINE OF IDEAS, &c.
The Platonic doctrine of Ideas has been, in all ages, the derision of the vulgar, and the admiration of the wise. Indeed, if we consider that ideas are the most sublime objects of speculation, and that their nature is no less bright in itself, than difficult to investigate, this opposition in the conduct of mankind will be natural and necessary; for, from our connection with a material nature, our intellectual eye, previous to the irradiations of science, is as ill adapted to objects the most splendid of all, “as the eyes of bats to the light of day[5].” And yet (as I presume, it will appear from the following discourse), unless the existence of these lucid beings is admitted, there can be no such thing as science; nor, indeed, any genuine knowledge at all. Hence, an enquiry concerning their nature and reality, is highly proper, as an introduction to the ensuing Commentaries, in which they are considered as the stable pillars of all truth, and the prolific principles of the universe.
[ii]
But previous to this enquiry, it is proper to observe, that Plato was not the inventor, though he was a strenuous asserter, of ideas; for, in the Sophista he affirms, that ideas were the discovery of men who excelled in wisdom and piety, and who contended for an invisible essence. Diogenes Laërtius, indeed, asserts, that Plato received the doctrine of ideas from Epicharmus. But Epicharmus was not their inventor, because Pythagoras, and others of still higher antiquity, were well acquainted with ideas; so that it may be affirmed, with much greater truth, that Plato was instructed in their nature by Philolaus his preceptor, and the disciple of Pythagoras. For Pythagoras, after his mysterious manner, signified ideas by numbers. But, prior to Pythagoras, Orpheus was an asserter of ideas, and called Jupiter, or the dimiurgus of the world, “the idea of all things.” And, according to Syrianus, the mundane sphere, celebrated by Empedocles, is no other than the ideal world; so that the doctrine of ideas is as ancient as that of wisdom itself.
But to begin with our enquiry: in the first place, without universals there can be no science; for the flowing and perishing nature of particulars is perfectly foreign from that stability and duration which is requisite to objects of invariable truth. Neither is it possible, that infinite individuals can exist without the subsistence of one cause endued with infinite power; for all multitude must necessarily originate from one, and must resemble its cause in as great a degree of perfection as its nature can admit; by a diffused infinity, shadowing forth that infinite power which subsists in indivisible union. Hence, if this be the case, and if infinite men, horses, and a multitude of other univocals, are produced in an infinite time, an unity of infinite power must be the source of each, according to which they are[iii] generated in a terminated manner to infinity in the universe. Again, all animals are transmuted from that which is in capacity (i. e. seed), into energy. But if this be true, it is requisite there should be some animal in the universe, subsisting in ever-vital energy, which may call forth that which is concealed in dormant capacity, into perfect actuality. Thirdly, the celestial orbs would not perpetually revolve in the same spaces, and after the same manner, unless one and the same universal number, or idea, ruled in each. So, likewise, there is a natural number in every animal; or those of the same species, would not always (when perfect) be distinguished with the same invariable organs; nor would they be subject to puberty and old age, at the same time, unless they were detained by the same measure of nature. Besides, the participation of universals, is evident in every sensible object. Thus, the rational nature is united with every individual man. Thus, animal subsists in a lion and a horse, in a man and a dog. And thus the pentad, or number five, is participated in the five fingers, and the duad in the nostrils, eyes, hands, and feet. But since these do not subsist without a cause, but are perfected by certain determinate natures, it is necessary there should be an universal animal, in the whole of nature, separate from sensibles, by means of which this sensible animal is generated. And that there should subsist in nature a pentad, through which the hands are always adorned with that number of extremities; and a duad, from which the two eyes and nostrils are derived. But if nature does not possess these numbers from herself, as she is not the first cause of all, but derives them from another cause, in the same manner as matter from nature, it is necessary there should be universals and numbers prior to nature, subsisting in far greater purity and perfection.
[iv]
Again, we may demonstrate the existence of ideas as follows: if the Deity, in fabricating the universe, operated essentially (and there is no other way in which we can conceive him to operate), he must fabricate the universe, an image of Himself. But, if this be the case, he contains in himself, in the manner of an exemplar, the causes of the universe; and these causes are no other than ideas. Besides, this consideration is not to be omitted, that the perfect must necessarily antecede and preside over the imperfect; unity over multitude; the impartible over the partible; and that which is perpetually the same, over that which admits of variation and change. From whence it may be inferred, that things do not originate from baser natures, but that their gradual processions end in these; and that they begin from the most perfect, best, and most beautiful natures. But let us pursue this reasoning more minutely, as it affords the strongest arguments for the existence of ideas.
When the Deity fabricated the various species of animals, and bestowed on them the different senses, it was doubtless with a view to the benefit of their possessors, as he foresaw, that without these, the animal could neither provide for its own support, nor defend itself from surrounding dangers. But may we not enquire from whence this previous perception originated? For it is not to be supposed, that he first made animals destitute of senses, and so, being admonished by their sudden destruction, afterwards assigned them to their nature. Shall we say, this foreknowledge was the result of a reasoning process? But then, we again ask, What were the principles of this ratiocination? For if they originated from other reasonings, it is necessary, at length, to arrive at something prior to these discursive operations, on which they ultimately depend; since all reasoning must[v] be founded on indemonstrable principles. Was sense, then, or intellect the principle of this previous perception? But, sense, in the present instance, had not then a being, for it could not exist prior to the animal nature: it was, therefore, intellect. But if intellect be the repository of certain propositions, and the conclusion be science, it must follow, that there could not then be a consultation of any thing sensible. For the principle and the conclusion must both depend on something intelligible. Besides, may we not ask, how such a habit of thought arose before the existence of a sensible nature! It is absurd in the extreme, to say from chance, and to resolve it into a sudden volition of the Deity, is an assertion that may, indeed, satisfy vulgar minds, but can by no means quiet the restless spirit of philosophical investigation. Since, to suppose the cause of the universe, actuated by sudden volitions, is to place him on a level with the vilest natures, and subject him to the irrational impulses of the brute. Hence we infer that the formation of animals, and by the same arguments of the world, was not the result of any reasoning process. For, indeed, argument and foreknowledge cannot with propriety be attributed to the Deity; but when they are ascribed to him, we must consider it as nothing more than an indication of his constituting particulars, in a manner somewhat similar to the providence of a wise man, in inferior concerns. For, in subordinate natures, whose operations cannot take effect prior to enquiry, reason is necessary, on account of the inferiority of that power which precedes the reasoning energy. In like manner, foreknowledge is necessary, because a power is wanting to its possessor, which might render him superior to its use. For foreknowledge is directed to this end, that one particular circumstance may take place in preference to another. But if it be requisite[vi] that every energy in the Deity should be void of defect, and if it is not lawful that any thing should be present with him, which is not total and universal, it is necessary that all things should be contained in every thing essential to the nature of the Deity. Hence, since even futurity is with him present, there is nothing in him posterior; but what is present in him becomes posterior, by its participation in another. If then futurity be present with the Deity, it is necessary it should be so present, as if foreknown in a posterior nature; that is, in such a manner that nothing may be wanting to any being; and that is, lastly, so that every thing may be complete.
Besides, reasoning cannot, by any means, belong to an eternal essence like the deity; for if this be admitted, he must be forgetful of his former operations. And if, in consequence of reasoning, he produces more perfect natures afterwards, his works could not be perfectly beautiful before: but if they were beautiful before, they must be co-existent with their cause, i.e. they must be eternally beautiful, antecedent to the reasoning energy. Again, if we suppose the supreme intellect, the demiurgus of the world, to operate by enquiry, his energy could not be spontaneous, and truly his own; but his essence would be similar to that of the artificer, who does not derive his productions from himself, but procures them as something adventitious by learning and enquiry. But if the universe was not formed by deliberation, it must be co-existent with its cause, and reside in his essence; for if it be not co-existent there must have been some particular time, in which its artificer determined on its production; and this determination must have been the result of a reasoning process, concluding that it would not be good to produce it before that particular time, (from whence, by the way, we infer the[vii] eternity of the world.) And if the universe be co-existent with its author, it must perpetually emanate from his nature, and be dependent on it, like the shadow on its forming substance. But in this case, its archetype must be contained in the essence of its author; for every cause is that primarily, which its effect is secondarily. And hence we infer, that if the sensible universe be replete with forms of every kind, the exemplars of those forms, must subsist in immaterial perfection, in the artificer of the world.
If this sensible world, then, be formed according to the exemplar of that which is intelligible; may we not say, with the great Plotinus, that it is requisite universal animal should there primarily subsist in perfect vital energy, containing all things in its omniform essence. “Hence (says he[6]) the heavens are there a divine animal, replete with ideal stars. Earth too does not there subsist solitary, but is much more vital than this corporeal earth, for it is full of intellectual life. The sea too is there, and all water subsisting in life, and an ever-abiding stream. For how is it possible that any thing not vital, can be the progeny of life itself? He, therefore, who enquires from whence animals originate in the intelligible world, might as well enquire from whence all life, and soul, and universal intellect, arose. For here there is nothing indigent nor defective, but every thing is perfect and exuberant. Here they all flow from one fountain, not as from a certain spirit, or heat, but as if from an universal quality, possessing and preserving in itself, all qualities; such as sweetness, accompanied with fragrance of smell, the vigour of wine, and the strength of all juices, bright colours, and whatever is perceived by the taste.”
[viii]
3. Such then are the arguments which the Platonic philosophy affords in defence of ideas; the existence of which was so evident to Plato, that, in the Sophista, he compares those who oppose the friends of ideas to the giants of old, warring, as it were, on celestial souls, and such as are engaged in sublime investigations. Let us now consider to what universals these lucid beings are confined; since, according to the Pythagoreans and Platonists, there are not ideas of all universal conceptions. “For, in the first place (says Syrianus[7]), there are no ideas of things evil and base, because these subsist in nature rather by a privation and absence of ideas. And, on this account, they are said to exist contrary to nature. Nor, secondly, of negations, for these are destructive of the bound and limitation which is attributed to every thing from the unifying and comprehending nature of ideas; and hence, separation is rather the result of material infinity than of that which is formal or ideal. Nor again, are there any ideas of things which at different times receive a variety of conditions. For these participate of transmutation from a moveable cause, but not from the immoveable and stable illustration of ideas. Nor again of parts, such as the hand, head, fingers, and the like. For the causes of things existing entire, produce whole species and forms; not divided about the parts of these, like the reasons of nature. But neither did these wise men place in intellect the determinate causes of accidents in bodies, such as sweetness and whiteness. For they considered that natural reasons were sufficient for the production of accidents. Nor again, of composites, as of a wise man. For[ix] since ideas are simple, they preside over the simple essence of every thing. But the composition and division of things is the business of our intellect; ideas, at the same time, and that intellection which is co-ordinate to ideas, being exempt from all these, on account of superlative simplicity. Neither, therefore, must we establish ideas of things generated from dissimilars, such as mules; nor of fruit produced by engrafting from different trees. For all these have a posterior and adventitious generation, and are not the work of nature alone, nor of nature proceeding according to her own reasons, but, as it were, compelled to labour contrary to her own determinations. Hence it is manifest, that all art, which imitates nature, and alone ministers to the use of mortal life, is separated from the cause of ideas. But neither are the works which, depending on the purpose of the soul, are perfected by a concourse of many causes, and which we are accustomed to call the operations of fortune, to be conjoined to the cause of ideas. For things which are there perfected, are eternal, and subsist perpetually the same, free from the nature of contingent events. It remains, therefore, that ideas must be confined to universal and perfect essences, and to whatever confers to their natural disposition; as for instance, to man, and every thing perfective of man, such as wisdom and virtue. For ideas existing as the generative and energetic causes of the perfection of every thing, distribute being to essences, and convert them to the inexhaustible plenitude of their own omniform natures.”
4. But let us now consider the nature of numbers; for as every form is a number, according to the Pythagoreans[8], a speculation of this kind must afford no small light to the[x] arduous investigation of ideas. Will it not, therefore, be proper, in the first place, to enquire, with the great Plotinus[9], whether multitude is not a departure and distance from one, so that infinity itself is a separation from unity in the extreme, because it is no other than innumerable multitude; that on this account it becomes evil; and that we contract a similar nature when departing from intellectual unity, we are divided by sensible multitude? For a being then properly becomes many, when no longer able to remain collected in itself, the same, it is diffused abroad, and thus, being dispersed, is variously extended; so that when, by diffusion, it is absolutely deprived of unity, it becomes perfect multitude, destitute of that universal cement, which unites one part with another. But whenever the conciliating one is present, then that which was scattered and diffused, becoming permanent by its bounding power, passes into magnitude. But if any one should deny the subsistence of unity, asserting that one is no where to be found, which is not some particular one; and should hence affirm, that what is called one abstractedly, is only a certain affection of the soul towards any being; we ask, what prohibits the appellation of essence, from being nothing more than an affection of the soul, and consequently the existence of being, a delusion? For we predicate unity of particulars with as great propriety as being. I am well aware, that philosophers of the present day will answer, that we have an evident proof of the reality of being, from its agitating the soul, and becoming apparent in the phantasy: to which we reply, that in like manner, the soul is agitated, and the imagination influenced about the one. For every individual as much excites the perception of one, as of being.
[xi]
Besides, it is necessary to enquire whether we behold this passion and conception of the soul, as one or multitude. And again, when we say not one, we do not then possess one from the thing itself; for we say that one is not contained in that individual. And hence we must possess one in our own nature, and this must reside in the soul, separate from that which is denominated some particular one. But here it may be objected, that the one we possess is received from externals, and is nothing more than a conception of the mind, produced by the thing itself. For it will be said, that as multitude is nothing besides a number of individuals, which are called many, so one is nothing besides one thing; and is formed by thought separating that one particular from others. To this we reply as follows:
How can it be consonant to reason to suppose that the conception of one arises from the sensation of some one particular subject? For one particular man, who is discerned by sense, is by no means the same with one itself, since, if this were the case, thought could never predicate one of that which is not a man. Besides, as cogitation, on beholding the different positions of things, affirms that this is here or there, so when it perceives an individual, pronounces one; for that passion is not vain, nor does it assert one of a non-entity. Nor must we think it predicates ones, because this individual is different from another; for when cogitation affirms such a thing is this, and not another, it declares, in the mean time, that the other is one. Likewise when it affirms that any thing is this alone, it then declares, that what is alone is one: on which account, it predicates one, prior to alone. Besides, if there be multitude, it is necessary that one should antecede; since when it predicates many, it pronounces more than one. And[xii] when it affirms that an army contains a multitude of men, it conceives the soldiers reduced to one order.
For thought, indeed, does not permit multitude to remain perfect multitude, destitute of the conciliating power of unity; in which very circumstance, the subsistence of one is evinced; for acutely and swiftly perceiving the one which results from order, it reduces the nature of the many into one. Besides, we affirm that a house and an army are each one, but that a house is more one than an army, on account of the continuity of its parts. If therefore, one is contained more in that which is continued than in that which is discrete, and still more in what is perfectly indivisible, it is evident that the one is a certain nature, and has a real being. For it is impossible that the more and the less should take place among things which have no subsistence. If then it be not possible to understand any thing without one or two, or some other number, it is by no means proper to deny existence to that, without which we cannot comprehend the existence or properties of any being: but it is requisite that nature should antecede all discourse, and intelligence, which is every where necessary to their existence.
Again, if unity has no real subsistence, and is nothing more than a name or conception of the mind, it may be destroyed without the destruction of its subject. The unity, therefore, of a house may be taken away, without the ruin of a house. But if a house is nothing more than certain materials, reduced into one form, this is impossible. And, on the contrary, the alteration of that subject, of which unity is predicated, can make no real alteration in unity (on this hypothesis) any more than the death of a man can affect his name. When, therefore, a body, of which one was predicated, is divided into a multitude of[xiii] parts, there is no real alteration made in the unity of the body, because unity is nothing more than a name.
It was in consequence of this reasoning, and perceiving that unity was participated by every being, that the Pythagoreans placed a super-essential one at the top of the universe, intelligibly abstracted from all beings in simplicity and excellence of nature. For they considered, that unless there was a self-subsisting one in all things, there could neither be universals nor particulars. Not the first, because they are by nature one and many. But it is requisite that the one itself, should preside over that which is not one alone. Nor again, the second, because they are many and one, (that is, they participate more of multitude than unity, and their nature is determined more by the many than the one.) And because of things in participation, unless an unparticipated one is added, there can be no cause of union to beings; in the same manner as the cause of essence to beings, is taken away by those who deny that being itself, is the principle of all essence. For as the good itself, is the one principle of good to the universe, and is nothing besides good; and as a self-motive nature, which is nothing besides self-motion, is the cause of motion to all things; so all things proceed from being itself, and all united natures receive their union from the one, abstracted from all things.
Hence (such is the absolute dominion of unity), continued quantities would have no existence without its participation; for when they are divided, so far as they lose unity, they change their being into some other form. Hence, the bodies of plants or animals, which are each of them one, when they fly from unity, and are dissipated into multitude, immediately lose the essence they formerly possessed, and become something else; which new state of[xiv] being they likewise possess so far as they are one. Add too, that health then flourishes in the corporeal frame, when the body is conciliated into one; then beauty flourishes, when the power of one connects the members into proportion and consent; and then virtue reigns in the soul, when the soul is reduced into one similitude with that which is divine.
5. But let us now investigate the nature of numbers. All number, according to the Pythagoreans, originates from unity and the indefinite duad; the first having the relation of form, and the second, that of matter to all the orders of numbers. But they likewise divided number into two kinds, essential and monadic. The essential number they considered as first subsisting in the intelligible world, together with being, and from thence distributed into all the various gradations of forms. But the monadic, or that which is composed from certain units, they justly considered as nothing more than the image of essential number. And with respect to the numbers which the human soul participates, these from its imperfect condition have a middle subsistence; i. e. they exist in a vital, gnostic, and speculative, but not in an operative manner. Hence, when receiving one thing with another, we affirm, that they are two, as a dog and a man, or two men; or when we compute more than two, as ten, and say that there is a decad of men, this number is not essential to the two or ten individuals, nor is it to be conceived as subsisting in sensible natures; but it is purely quantity. But when we distribute this ten, into units, we produce the principle of quantity, and generate a subject in opinion[10], capable of[xv] participating the essential decad of our soul. But when, considering man in himself, we affirm that he is a certain number, as the duad, composed of animal and rational, we do not observe one mode in this predication; but so far as by a discursive operation of the soul, we numerate, we effect a particular quantum; but so far as the subjects are two, and at the same time both one (since one fills the essence of both, and in both unity is contained), we pronounce another, and an essential number: and this duad is not of a posterior origin, nor alone signifies a certain quantity, external to the subject, but a duad subsisting in the essence of man, and containing his nature. For here we do not produce a number by a discursive operation, while we pursue essential natures. But when we number any ten things, which are not connected by any conciliating unity, like a choir, or an army, then this decad, which we predicate of the ten particulars, subsists alone in our numerating soul, which renders the ten individuals in opinion, a definite quantum. But in a choir, or an army, essential number is participated exclusive of that which subsists in our soul. And if it be enquired how number subsists in the human soul, we must say, that the soul, by her self-moving energies, procreates number, while she numerates, and by this energy, causes the existence of quantity; in the same manner as in walking, we give rise[xvi] to a certain motion. Thus, monadic number, or a collection of units of various kinds, subsists in opinion, in a manner correspondent to that of geometrical figures; and by this means participates the essential number of the soul. For as a triangular figure in the phantasy, is the recipient of a triangular nature, or of triangle itself; so every three units in opinion, receive the essential triad of the soul, and, by this means, form a definite quantum.
In short, as in every being we may discern the resemblances of matter and form, so in the pentad, or any other number, the five units, which are the subject of participation, and the quantity of the number, originate from the duad; but the form, that is the pentad itself, from unity. For every form is an unity, which unites its subject quantity, and connects it with its ideal species. It is, therefore, requisite to understand, that the two principles of mathematical numbers are resident in our souls, with which every mathematical number is co-existent; I mean unity, comprehending in itself all the forms of numbers, and which corresponds to unity in intellectual natures; and the duad, endued with a generative power, of a formless nature, and of infinite virtue; and which is called boundless, on account of its being the image of never-failing and intelligible duality. Hence, the unity of the soul, with a never-ceasing energy, continually distinguishes and forms all the orderly processions of her numbers, suffers no vacuum to intervene, and leaves no quantity formless and innumerable. Hence too, no essential number of the soul, as for instance, the pentad, is composed from substance and accident, as a white man; nor from genus and difference, as man from animal and biped; nor again, from five unities mutually touching each other, like a bundle of wood; nor from things mixt, like water and[xvii] wine, nor from things subsisting by position, in the manner that stones compose a house; nor lastly, does it subsist like things numerable; for it is not because they are composed from indivisible units, that they possess any thing besides units. For many points are indivisible, yet quantity is not produced on this account; but because they participate of two natures, the one corresponding to matter, and the other to form. Lastly, it is not proper to say, that the number seven (and so of any other number), is composed from the triad and the tetrad; for units, indeed, composed with units, form a subject adapted to the reception of the heptad, or the ideal and essential number seven; but the definite numerical quantity seven, is formed from so many units, and the ideal heptad. Hence, as the soul of the shipwright gives form to the timber, from her inherent art; so the numerative soul, from the unity endued with the relation of a principle which she possesses, gives form and subsistence to all her inherent numbers. But there is this difference between the two, that the shipwright’s art is not essential to our nature, and requires manual operation, because it is conversant with sensible matter; but the numerative art is essentially inherent in the soul, and is therefore present with all men, and possesses an intellectual matter, which it easily forms without the assistance of time. And this, perhaps, is what deceives many, who think that the heptad is nothing more than seven units. For the imagination of the vulgar, unless it first perceives a thing destitute of ornament, and afterwards the operations of the adorning artificer supervening its nature; and lastly, beholds the thing perfect, and invested with form, cannot be persuaded that it possesses two natures, the one formless, but the other endued with an energetic and forming power.
[xviii]
And here it is necessary to observe, that though unity is the form of all arithmetical forms, yet it is chiefly the form of the decad. For what unity is simply to all the series of numbers, that the decad is to the following hundreds, thousands, and millions; from whence, according to a secondary progression, it is denominated unity. As intellect, therefore, is the form of all things, but especially of the soul, so unity, though it is the idea of all numbers, yet especially of the decad. But the reason why the Pythagoreans extended ideal numbers no farther than ten, is because this number is the ultimate perfection of beings, containing all things in its omniform nature. For all proportion subsists within the number ten; the arithmetical in a natural progression of numbers from unity; the geometrical in the numbers 1, 2, 4, and 1, 3, 9, and the harmonical in the numbers 2, 3, 6, and 3, 4, 6. And since the causes of all things are contained in numbers, as far as to the decad[11], it is superfluous to suppose exemplars of the following numbers.
If it should be asked in what manner we must conceive number as subsisting in the intelligible world, we answer, with the great Plotinus, that we must conceive it as subsisting in being itself, with a power of impelling it to the production of multitude. “Hence (says he, Ennead vi. lib. vi.) number is either the essence or the energy of being, and animal itself, and intellect is number. But, perhaps, we must call being, number united (ἀριθμὸς ηνωμένος), but beings, number evolved, or unfolded; (ἐξεληλεγμένος ἀριθμὸς) intellect, number moving in itself; (ἀριθμὸς ἐν ἐαυτῶ κινούμενος)[xix] and lastly, animal, number comprehending (ἀριθμὸς περιέχων.“) It was in consequence of this reasoning, that the Pythagoreans called ideas numbers; because the gradual evolution of these from ineffable unity, produced all the beautiful variety of forms. Their exalted conceptions of numbers, likewise, originated from the same sublime theory. Hence, [12]Pythagoras, in the sacred discourse, calls number “the ruler of forms and ideas.” But [13]Philolaus, “the commanding and self-begotten container of the eternal duration of mundane concerns.” And [14]Hippasus, and all those who were called ἀκουσματικοὶ (or such as were yet under the probation of the quinquennial silence), “the first exemplar of the mundane fabric, and the judiciary instrument of its artificer.”
6. And here I cannot but take notice, with regret, of the very unphilosophical mistake committed by that great mathematician Dr. Barrow[15]: I say, with regret, on account of the extraordinary obligations I am under to his writings, for my proficiency (whatever it may be) in mathematical learning. But respect must yield to the truth. “Unity, says he, is not indivisible. (For how ex. gr. can 2/6 added to 4/6 be equal to unity, if unity be indivisible and incomposed, and represent a point) but rather only unity is properly divisible, and numbers arise from the division of unity.” Here the Doctor evidently confounds sensible units, which are the subjects of vulgar practical arithmetic, with those units which are the objects of science. Every individual sensible object, is indeed an unit, so far as it[xx] participates the connecting and conciliating power of an immaterial one: but the unity which stands at the top of speculative arithmetic, is perfectly indivisible, or arithmetic would cease to be a science. The truth of this is evident from Euclid’s definition: “Unity (says he) is that according to which each of the things which are, is called one.” But if unity be a composite, the definition is false; since a composite, or a certain multitude, can never be the cause of unity, but the contrary. And that this immaterial one subsists in sensible natures, has, I hope, been sufficiently proved in the preceding part of this discourse. But the Platonic Theo[16] of Smyrna, fully establishes the indivisibility of unity, as follows: “Unity is terminating quantity, the principle and element of numbers, which remains undiminished by the most immense multitude of subtractions, and being deprived of all number, continues firm and fixt, because it is impossible for division to proceed beyond the bound of unity. Thus, if we separate any one corporeal substance into parts, the one again becomes many; and by subtracting the several parts, we end in one part; and from this remaining part, again divided, arises multitude; and by taking away every part, we again arrive at one. So that one, considered as one, is incapable of diminution, and perfectly indivisible. On the contrary, every number is diminished by division, and is separated into parts less than itself; as the number 6 into 3 and 3, or into 4 and 2, or into 5 and 1. But unity in sensible particulars, if divided, is diminished after the manner of body, and by section is distributed into parts less than itself: but it receives increase after the manner of number; for instead of the one, multitude is produced. In this sense, therefore, is unity indivisible; for nothing is divided into parts greater than[xxi] itself. But that which is cut into parts greater than the whole, and into parts equal to the whole, is divided as number. Thus, for instance, if any one sensible body is divided into six parts, 1, 1, 1, 1, 1, 1, these shall be equal to the whole; but by a section into 4 and 2, it is divided into parts greater than the whole, considered as one; for 4 and 2 considered as numbers, exceed unity, and the body was supposed to be one. Unity, therefore, as number is perfectly indivisible. But unity is called by the Greek word μονάς, only, or alone, either because it remains immoveable, and does not desert itself, nor surpass the bounds of its nature (for it remains the same, however multiplied into itself, through an infinite progression) or because it is placed separate and apart from the multitude of other numbers, it is denominated the monad, or one.”
In consequence of this very mistaken hypothesis, which opposes not only all the wisdom of antiquity, but the sublimest truths, the Doctor asserts, that an arithmetical cypher is the principle of numbers; and that it is analogous to a point in geometry. Just as if a cypher, which is nothing more than a mark expressive by its position with numbers, of a certain quantity, had a real existence, and was productive of number: when, at the same time, any other arbitrary character would serve the same purposes, if applied in a similar manner. It must surely afflict every thinking mind, to see how dreadfully the mechanical system of philosophy, which has been so long in fashion, enslaves and perverts the minds of its votaries; for there cannot, I think, be a more egregious instance of its fatal tendency, than the present, in which nothing is considered as the foundation of that noble science, arithmetic; which was deservedly placed by the ancients, in the first rank of the mathematical disciplines. Such a foundation, indeed, may[xxii] be proper to the mechanical philosophy, but is very ill adapted to support the solid fabric of the arithmetical science. But let us attend to the arguments of this most learned man, in defence of so strange an assertion, “A cypher, or arithmetical nothing (says he) is really the bound of every number coming between it and the numbers next following, but not as a part. A cypher being added to, or taken from a number, does neither increase nor diminish it; from it is taken the beginning of computation, while itself is not computed; and it bears a manifest relation to the principal properties of a geometrical point.” But in what manner are we to conceive the nothing which intervenes between any two numbers, to be their term or boundary? For Euclid defines a term to be the extremity of any thing; implying by the extremity, something belonging to that of which it is the bound. But how can a cypher, or nothing, in any respect belong to number, or something? For if nothing be a boundary, merely from its intervention, a point existing between any two disjoined lines, though at the greatest distance from each, must be their common boundary, which is evidently absurd. Besides, what relation does it bear to a point, which is endued with a generative power, by its flux forming the simple extension of a line, and, at the same time, every where limiting its progression, and subsisting in infinite capacity in its every part? Where are the real and divine properties to be found in an arithmetical nothing, which Proclus, in the following Commentaries, exhibits in a point? And how can computation originate from a mere non-entity?
But a little consideration will convince us, that this Saracen, or Indian cypher, is nothing more than an arbitrary character, invented for the purpose of facilitating computation. For, suppose the letter (a) to be placed in[xxiii] its stead, and to signify, when connected with the mark for unity, ten, or ten multiplied by one; when connected with the mark for two, ten multiplied by two, and so on. And again, when placed twice after unity, let it express the second power of ten, or one hundred, in this manner, a a; when thrice connected, one thousand, or the third power of ten, and so on: shall we say, in consequence of this, that (a) is the bound of numbers, and the principle of arithmetic? Or, shall we not rather say, that it is an arbitrary symbol, like any other algebraic character, having no real connection with numbers, and depending, for its existence and application, entirely on the will of its inventor. But this opinion is too absurd to need any farther refutation.
7. It may here, perhaps, be expected, that I should explain how, in the language of Syrianus[17], “divine number proceeds from the immortal retreats of unity, until it arrives at the divine tetrad[18];” and that I should unfold the properties of the tetractys, according to the Pythagoreans; but an undertaking of this kind, would not only far exceed the limits of this dissertation, but, perhaps, in the present age, might be justly deemed, by the lovers of wisdom, a prostitution and profanation of the most exalted truths. Enough, I hope, has been said to excite the curiosity, and rouse the attention of the thinking and liberal part of mankind; and those who understand what is here briefly delivered, may apply themselves, with advantage, to Proclus on Plato’s Theology, where they will find all the mysteries of numbers unravelled; and to the works of the great Plotinus, who will lead them into the penetralia[xxiv] of the most recondite wisdom. But, in perusing the works of these great men, the reader must not expect to find the sublimest truths explained in a familiar manner, and adapted, like many modern publications, to the meanest capacities. For this, indeed, is impossible to be effected. “Mankind (says Petvin[19]), are not to be made any more truly knowing than happy by another’s understanding.—There is no man can at once convey light in the higher subjects, to another man’s understanding. It must come into the mind from its own motions, within itself: and the grand art of philosophy, is to set the mind a-going; and, even when we think nothing of it, to assist it in its labour.” After which he observes, that “the ancients never attempt to lead us into knowledge, by a continued chain of reasoning; on the contrary, they write in such a manner, as to force us to think for ourselves.” And, previous to this, he remarks, “that there are certain truths acquired by a long exercise of reason, both in particular, and likewise in those subjects that are most general, as much, perhaps, out of the reach of the greatest mathematician, as Sir Isaac Newton’s speculations are above the capacity of some that are now called mathematicians.” The truth of this observation is sufficiently evinced, in Plato’s definition of a philosopher (in his Sophista), “The philosopher (says he) is the man who sufficiently sees one idea every way extended through many, every one of them lying apart; and many ideas different from one another, externally comprehended under one.—And farther, one idea, throughout all manys, wrapt up in one; and many ideas, every way separate or discreet. This is to have the knowledge to discern how ideas, as they are general, agree and disagree.” Now, he who thinks that a perception of this kind may be acquired[xxv] by barely reading an accurate discourse on the nature of ideas, composed in intelligible terms, without, at the same time, employing a long course of profound meditation, and patient thought, knows but little the difficulty of the task, and until he changes his opinion will never be the wiser. But the folly and presumption of men, with respect to this sublime philosophy, is really unpardonable; for there are very few who conceive that much previous instruction is requisite to its acquisition; but almost every man decides peremptorily on the most abstract speculations, and reckons himself sufficient for the most profound investigations. In the sciences and arts they are willing to proceed to perfection by gradual advances; but they consider philosophy as easy, of instant access, and hastily approach to her embraces with an assured confidence of success. Though, like unhappy Ixion, through their presumption, instead of a goddess, they grasp nothing but an empty cloud. Plato was so sensible of this truth, that, in his seventh epistle to Dion, he expressly affirms, that he neither has written, nor ever will write explicitly concerning these sublime speculations; “For a thing of this kind (says he) cannot be expressed by words, like other disciplines, but by a lasting familiarity, and conjunction of life, with this divine object, a bright light[20][xxvi] on a sudden, as it were leaping from a fire, will illuminate the soul, and there preserve and nourish its splendor. He adds, that a publication of such concerns, is alone useful to a few of mankind, who from some small vestiges previously demonstrated, are sufficiently sagacious to their invention. But it will fill others partly with a base contempt, and partly with a rash and vain confidence, as if they had now learned some very excellent things.” He then subjoins the following instance of the difficulty attending such an undertaking: “There are three things (says he), from which science must necessarily be produced; but the fourth is science itself. And it is requisite to establish the fifth as that which is the object of knowledge, and has a true existence. One of these is the name of a thing; the second its definition; the third the resemblance; the fourth science. Now take each of these, desiring to learn what we have lately asserted, and think concerning them all, in a similar manner. A circle is called something, whose name we have just expressed. After this follows its definition, composed from nouns and verbs. For that which every where is equally distant from the extremes to the middle, is the definition of that which we signify by the name of a round, and a circumference, and[xxvii] a circle. But the third is the circle which may be painted, or blotted out, which may be made by a wheel, or destroyed. None of which affections, the circle itself, which each of these respects, suffers, as being of a different nature. But the fourth is science, and intellect, and true opinion about these. And this again must be established as one whole, which neither subsists in voice, nor in corporeal figures, but in intellect and intelligence. It is therefore manifest, that this fourth is different from the nature itself of the circle, and again different from the three we have previously mentioned. But among the number of these, intellect, by its relation and similitude, proximately adheres to the fifth, while the rest are more remote from its nature. The same may likewise be affirmed of a straight and crooked figure, of colour, and of the good, the beautiful, and the just. And again, of every body, whether fashioned by the hand, or the work of nature, whether fire or water, and the rest of this kind; likewise of every animal, and the manners of animals; and of all actions and passions. For unless, among these, some one, after a manner, receives that fourth, he will never perfectly participate the science about the fifth.” He then proceeds to shew in what respect each of the preceding four are different from the fifth. “Every circle (says he) which by the hands of men is either painted, or fashioned by a wheel, is plainly contrary to our fifth. For it every where participates of the right-line. But we must affirm, that the circle itself has neither more nor less of any thing whatever; that is, it possesses in itself, nothing of a contrary nature. Besides, none of these are endued with any stability of name. For nothing hinders our applying the appellation of straight to that which we now denominate round, and calling the straight by the denomination of the round; nor will there[xxviii] be any less stability in these, when their names are changed into the contrary. The same reasoning is likewise true of definition, since it is composed from nouns and verbs, which possess no stability. And in a variety of ways, it may be proved, that no one of these four is certain and firm.” Now, this fifth division of Plato’s entirely respects ideas, considered as flourishing in intellect; by a conjunction with which, we acquire true intelligence, and the perfection of human knowledge. The first three of the preceding are obnoxious to various mutations; the fourth less; but the last is perfectly stable and invariable. The three first are rather conversant about the qualities of things, about the image and shadow; the fourth raises us to the participation of truth; but the fifth to truth itself, and permanent essence. In the first degrees almost all are conversant; in the fourth a few; in the fifth, all the gods, but a very small part of mankind, as it is asserted in the Timæus. The four first may be known, indeed, without the fifth, confusedly; but from the knowledge of the fifth they become perfectly manifest, as effects from the knowledge of their cause. But we cannot, by any means, attain to the apprehension of the fifth, unless we have been first accurately conversant with the rest; for from our imperfect condition we are compelled to rise from difference to identity, from multitude to unity, and from shadow to substance. While we investigate the knowledge of things, if we are alone desirous to apprehend their resemblance (which is the case with the multitude) we shall be placed in the third degree, and may easily acquire the object of our pursuit. But if we should fortunately possess the true philosophical genius, which is rare in the extreme, and aspiring to the fifth degree, should, by a happy event, attain to its conjunction, though such a contact is clearer and[xxix] more certain than all knowledge; yet it is difficult to express it in words, and to manifest it to others. And the reason of this is obvious: first, because words are wanting, which exactly correspond to the essence of a thing, since these are only the symbols of shadows. Secondly, because we speak with those, who are alone conversant with shadows, and are on this account derided by them, when they find that our fifth does not, by any means, accord with material resemblances, which they consider as the only realities.
8. And here a question very naturally presents itself for our solution, whether the soul, while united with the body, is able to perceive ideas, without the assistance of the phantasy, For it seems difficult to apprehend how the soul, thus depressed and weighed down with the terrene mass, should be able to raise herself to the supernal light of ideas, and become united with their refulgence. The opinion of the Peripatetics is well known, that some phantasm must always accompany intelligence; but this is denied by the Platonists, and I think with great reason. For the operations of intellect are not dependent on the phantasy, though the perceptions of the latter proceed from the energies of the former. Besides, as Plotinus beautifully observes, our most vigorous energies are accompanied with the least animadversion; and there is no absurdity in supposing that by increasing the force of intellectual energy, we may speculate free from all imagination; since the phantasms attending our conceptions, became weak in proportion as the intellectual sight increases in vigour. On this account, the Platonists affirm, that the moral virtues free us from the vehemence of perturbations; but the contemplative from imagination, and the senses. Hence too, the sciences may be called living waters; in which the[xxx] wings of the soul being dipt, her feathers, which were either separated or broken by her lapse into body, are repaired, and restored to a resemblance of their former perfection. For the wings are the powers of the soul, leading to intelligibles: but the feathers are as well the natural instincts to good and truth, as reasons inserted in the soul; which either fall off, or are broken by her descent into body, and conjunction with its ruinous bonds. But these are repaired and invigorated by the sciences, which, like living streams, flowing from the fountains of ideas, restore life and perfection to the soul. Hence Plato, in the Phædrus, asserts that these wings of the soul are increased by every thing which confers to supernal elevation; as beauty, wisdom, and the like; and by a convenient metaphor, in the same dialogue, he considers the chariot of the souls lives, her charioteer, and the horses by which her car is drawn; and lastly, every thing which contributes to the elevation of the soul, and her conjunction with intellect and ideas. We may therefore conclude, that this conjunction is possible to be effected, though it is rarely obtained; and that it is a flight too arduous and sacred for the groveling and sordid; a splendor too bright for the sensible eye; and a contact too ineffable to be described by the unstable composition of words.
But I cannot conclude this section, without soliciting the reader’s attention to a comparison of the difference between the ancient philosophy, and that invented by Mr. Locke, and the moderns. According to Mr. Locke’s system ideas are formed from sensible particulars, by a kind of mechanical operation; so that truth is something by its nature, posterior to sensation, and entirely dependent on it for existence. According to Plato, ideas are eternal and immaterial beings, the originals of all sensible forms, and[xxxi] the fountains of all evidence and truth; so that on this system truth ranks among the first, and not in the last of things; and would still retain its nature, though the corporeal senses were no more. According to Mr. Locke, the soul is a mere rasa tabula, an empty recipient, a mechanical blank. According to Plato, she is an ever-written tablet, a plenitude of forms, a vital and intellectual energy. On the former system, she is on a level with the most degraded natures, the receptacle of material species, and the spectator of delusion and non-entity[21]. Hence, her energies are nothing but somnolent perceptions, and encumbered cogitations; for all her knowledge terminates in sense, and her science in passion. Like a man between sleeping and waking, her visions are turbid and confused, and the phantoms of a material night, continually glide before her drowsy eye. But on the latter system, the soul is the connecting medium of an intelligible and sensible nature, the bright repository of all middle forms, and the vigilant eye of all cogitative reasons. Hence she is capable of rousing herself from the sleep of a corporeal life, and emerging from this dark Cimmerian land, into the regions of light and reality. At first, indeed, before she is excited by science, she is oppressed with lethargy, and clouded with oblivion; but in proportion as learning and enquiry stimulate her dormant powers, she wakens from the dreams of ignorance, and opens her eye to the irradiations of wisdom.[xxxii] On Mr. Locke’s system, the principles of science and sense are the same, for the energies of both originate from material forms, on which they are continually employed. Hence, science is subject to the flowing and perishable nature of particulars; and if body and its attributes were destroyed, would be nothing but a name. But on the system of Plato, they differ as much as delusion and reality; for here the vital, permanent, and lucid nature of ideas is the fountain of science; and the inert, unstable, and obscure nature of sensible objects, the source of sensation. On Mr. Locke’s system, body may be modified into thought, and become an intelligent creature; it may be subtilized into life, and shrink, by its exility, into intellect. On that of Plato, body can never alter its nature by modification, however, it may be rarefied and refined, varied by the transposition of its parts, or tortured by the hand of experiment. In short, the two systems may be aptly represented by the two sections of a line, in Plato’s Republic. In the ancient, you have truth itself, and whatever participates of the brightest evidence and reality: in the modern, ignorance, and whatever belongs to obscurity and shadow. The former fills the soul with intelligible light, breaks her lethargic fetters, and elevates her to the principle of things; the latter clouds the intellectual eye of the soul, by increasing her oblivion, strengthens her corporeal bands, and hurries her downwards into the dark labyrinths of matter.
Nor is it wonderful there should be so great a difference between the two systems, and so much in favour of the ancients, if we consider the great advantages these ancients possessed over the moderns in every thing which contributes to the advancement of philosophy. For, in the first place, they lived in an age when abstract investigations[xxxiii] were in the greatest request, and the professors of such pursuits in the highest estimation. Besides this, they united the most exalted abilities with the most unwearied attention and obstinate perseverance; they devoted their whole lives to the search of truth; and relinquished every thing which might be an obstacle to its acquisition. We may add, likewise, the advantages of a language extremely philosophical; and a freedom from the toil of learning any tongue but their own. Now the reverse of all this is the portion of the moderns: for in the present age, abstract speculations are ridiculed; and its professors despised. The pursuit of truth is considered as perfectly consistent with ordinary avocations, and is rather prosecuted as a relief from the toils of business than as a thing desirable for its own sake, and of the greatest dignity and worth. Hence, a few years desultory application at a college, where language is one of the first objects of attention, qualifies a modern for philosophy, raises him above Pythagoras and Plato, and persuades him, with presumptuous confidence, to enter the lists against these venerable heroes. And lastly, all modern languages are barbarous with respect to the Greek; falling far short of its harmony and energy, its copiousness and propriety. If such then be the true state of the case, what judgment must we form of men who, with all these disadvantages, philosophized without the assistance of the ancients, despising their works, and being ignorant of their contents? Shall we call it prudence or presumption, wisdom or folly? Truth will certainly pronounce the latter; and the general voice of posterity will confirm her decision. There are two egregious instances in our own country of this daring presumption; I mean Bacon and Locke. The former of these is celebrated for having destroyed the jargon of the schoolmen, and brought[xxxiv] experimental enquiries into repute; and for attempting to investigate causes through the immensity of particular effects. Hence, he fondly expected, by experiment piled on experiment, to reach the principle of the universe; not considering that his undertaking was as ridiculous as that of the giants of old, who attempted to invade the heavens, by placing Ossa upon Pelion, and Olympus upon Ossa; and ignorant that
The latter of these, Mr. Locke, is applauded for having, without assistance from the ancients, explained the nature, and exhibited the genuine theory of human understanding. But that this applause is false, the preceding comparison between his and the ancient philosophy, may evince; and the variety of other self-taught systems which, like nocturnal meteors, blaze for a while, and then vanish in obscurity, abundantly confirms. Had these men, indeed, when they justly derided the barbarous writings of the schoolmen, explored the works of antiquity, penetrated the wisdom they contain, and enriched their native language with its illustration, they had doubtless been celebrated by the latest posterity: but, desirous of becoming masters in philosophy by intuition, they disdained the instruction of the ancients, and vainly attempted to soar on artificial wings to the very summit of science. They are, however, destined, like Icarus, to a precipitate fall; for the influence of time, which is continually dissolving the cement of their plumes, is likewise continually weakening their force, and will at last effect their final separation. And thus much concerning the doctrine of ideas, and numbers, according to Pythagoras and Plato.
[xxxv]
But let us now consider the properties of the demonstrative syllogism, and endeavour to unravel its intricate web; appointing Aristotle for our guide in this arduous investigation. For an enquiry of this kind is naturally connected with the doctrine of ideas, as it enables us to gain a glimpse of the universals participated in mathematical forms, and to rise to the principles of science. It brings us acquainted with the laws which bind demonstration; and teaches us that objects of intellect are alone the objects of science, and the sources of truth.
Previous to the acquisition of all learning and ratiocinative discipline, it is necessary we should possess certain natural principles of knowledge, as subservient to our future progress and attainments. Thus, in every science there are some things which require an immediate assent as soon as proposed; whose certainty is too evident and illustrious to stand in need of any demonstrative proof deduced from that particular science which, like stately pillars, they equally support and adorn. Hence we are informed by the geometrician, that a point is that which is destitute of all parts whatever; but we must previously understand the meaning of the word part. Thus the arithmetician defines an odd number, that which is divided according to unequal parts; but it is necessary we should antecedently know the meaning of the word unequal. Thus, too, art as well as science operates by antecedent knowledge; and hence the architect,[xxxvi] the statuary, and the shipwright, learn the names and the use of their respective implements, previous to the exercise of the materials themselves. This is particularly evident in the discursive arts of rhetoric and logic; thus the logician reasons by syllogism, the rhetorician by induction, and the sophist by digressions and examples; while each proceeds in an orderly progression from principles simple and evident, to the most remote and complicated conclusions.
2. The antecedent knowledge of things may be divided into two parts: the one a knowledge of their existence, or that they exist; the other a knowledge of the terms expressive of their existence. Thus, previous to the enquiry why iron is attracted by the magnet, it is necessary we should learn the reality of this attraction, and the general mode of its operation: thus too, in an enquiry concerning the nature of motion and time, we must be previously convinced of their existence in the nature of things. The second division of antecedent knowledge takes place in subjects whose very existence admits of a dispute: thus previous to a solution of the questions, Whether there are any gods or not? Whether there is a providence or not? and the like, it is necessary we should first understand the meaning of the terms; since we in vain investigate the nature of any thing while we are ignorant of the meaning of its name; although, on the contrary, we may have a perfect conception of the meaning of some words, and yet be totally ignorant whether the things they express have a real, or only an imaginary existence. Thus, the meaning of the word centaur is well understood by every one; but its existence is questioned by most.
3. From hence it will easily appear, that no small difference subsists between learning and knowledge. He who is about to understand the truth of any proposition, may[xxxvii] be said to possess a previous conception of its truth; while, on the contrary, it may happen that he who is in the capacity of a learner, has no antecedent knowledge of the science he is about to learn. Thus we attain to the distinct knowledge of a thing which we formerly knew in a general way; and frequently, things of which we were ignorant are learned and known in the same instant.
Of this kind are the things contained under some general idea, of which we possess a previous knowledge: thus, he who already knows that the three interior angles of every triangle are equal to two right, and is as yet ignorant that some particular figure delineated on paper is a triangle, is no sooner convinced from inspection of its being a triangle, than he immediately learns and knows: he learns it is a triangle; he knows the equality of its angles to two right ones. That it is now a triangle he both sees and learns; but the equality of its angles he previously knew in that general and comprehensive idea, which embraces every particular triangle.
Indeed, a definite knowledge of this triangle requires two conditions: the one, that it is a triangle; and the other, that it has angles equal to two right. The first we receive from inspection; the second is the result of a syllogistic process; an operation too refined for the energies of sense, and alone the province of intellect and demonstration. But demonstration without the knowledge of that which is universal, cannot subsist; and since the proposition is universal, that in every triangle the angles are equal to two right; as soon as any figure is acknowledged to be a triangle, it must necessarily possess this general property.
Hence we infer, that of the triangle delineated on paper, and concealed, we are partly ignorant of this general property, the equality of its angles (because we are ignorant[xxxviii] of its existence); and we partly understand it as included in that universal idea we previously possessed. Hence too, it is evident that actual science arises from a medium between absolute ignorance and perfect knowledge; and that he who possesses the principles of demonstration, possesses in capacity the conclusions also, however complicated and remote; and that by an evocation of these principles from dormant power into energy, we advance from general and abstracted knowledge to that which is sensible and particular.
4. Two acceptations of knowledge may be admitted; the one common and without any restriction; the other limited and peculiar. Since all knowledge, whether arising from accidents, or supported by necessary principles, is called science. Knowledge, properly so called, arises from a possession of that cause from which a thing derives its existence, and by which we infer the necessity of its existence; and this constitutes simple and absolute science. Thus too, the definitions of those general conceptions and suppositions, which from their primary nature are incapable of demonstration, are called science. But the science which treats of the method of arriving at knowledge, is called demonstration; for every demonstration is a syllogism producing science. Hence, if in every syllogism it is necessary that the propositions should be the cause of the conclusion; and to know any thing properly, a knowledge of its cause is requisite; in the propositions of demonstration, both these conditions are required: that they should be effective of the conclusion; and the causes of the thing demonstrated.
Thus, from the ruins of a stately edifice, we may justly infer, that the building was beautiful when entire; and from the smoke we may collect the existence of the fire,[xxxix] though concealed: but the ruins of the edifice are not the cause of its beauty; nor does fire originate from smoke, but, on the contrary, smoke is the natural result of fire: the inference, therefore, is in neither case a demonstrative one. Again, since every cause is both prior to, and more excellent than its effect, it is necessary that the propositions should be more peculiar, primary, and excellent than the conclusions. And because we then know a thing properly when we believe it to have a necessary existence, hence it is requisite that the propositions should be true; for if false, a false conclusion may ensue, such as, that the diameter of a square is commensurable with its side. But if every science arises from antecedent knowledge, demonstration must be founded on something previous; and on this account it is requisite that the propositions should be more known than the conclusions. The necessary properties, then, of all demonstrative propositions, are these; that they exist as causes, are primary, more excellent, peculiar, true, and known, than the conclusions. Indeed, every demonstration not only consists of principles prior to others, but of such as are eminently first; for if the assumed propositions may be demonstrated by other assumptions, such propositions may, indeed, appear prior to the conclusions, but are by no means entitled to the appellation of first. But others, on the contrary, which require no demonstration, but are of themselves probable or manifest, are deservedly esteemed the first, the truest, and the best. Such indemonstrable truths were called by the ancients, axioms, from their majesty and authority; as the assumptions which constitute the best syllogisms derive all their force and efficacy from these.
And on this account, above all others, they merit the title of the principles of demonstration. But here it is[xl] worth observing, that these primary propositions are not the first in the order of our conceptions; but first to nature, or in the nature of things. To us, that which is first is particular, and subject to sensible inspection; to nature, that which is universal, and far remote from the apprehension of sense. Demonstration does not submit itself to the measure of our ingenuity, but, with invariable rectitude, tends to truth as its ultimate aim; and without stopping to consider what our limited powers can attain, it alone explores and traces out the nature of a thing, though to us unperceived and unknown.
This demonstrative syllogism differs not a little from others, by the above property; the rest can as well educe a true conclusion from false premises, which is frequent among the rhetoricians, as that which is prior from that which is posterior; such as, Is every syllogism derived from conjecture?
With respect to the rest, as we have already confessed, they may be formed from principles that are true, but not from such as are proper and peculiar; as if a physician should endeavour to prove an orbicular wound the most difficult to coalesce and heal, because its figure is of all others, the most capacious; since the demonstration of this is not the province of the physician, but of the geometrician alone.
5. That proposition is called immediate, which has none superior to itself, and which no demonstration whatever can confirm: such as these are held together by the embraces of universals. There are some, indeed, united from that which is sensible and particular: thus, that the garment is white, is an immediate proposition, but not of that kind whose principles require to be demonstrative ones; the cause of which we shall hereafter investigate. Of immediate[xli] propositions subservient to the purposes of demonstration, some are of such a superior nature, that all men possess a knowledge of them without any previous instruction; and these are called axioms, or general notions; for without these all knowledge and enquiry is vain. Another species of immediate propositions is position; incapable of being strengthened by demonstration, yet not necessarily foreknown by the learner, but received from the teacher. With respect to the genus of position, one of its species is definition, and another hypothesis. Definition is an oration, in which we neither speak of the existence, nor non-existence of a thing; but alone determine its nature and essence. It is common to every hypothesis, not to be derived from nature, but to be the entire result of the art of the preceptor.
It likewise always affirms the existence or non-existence of its subject: such as, that motion is, and that from nothing nothing is produced. Those which are not so perspicuous are called postulates, or petitions; as that a circle may be described from any centre, and with any radius; and such as these are properly hypotheses and postulates.
6. We have now seen the privilege assigned to the principles of demonstration:—whether or no our decision has been just, the ensuing considerations will evince. We said that the assumptions in demonstration were more known than the conclusions,—not indeed without reason, since through these our knowledge and belief of the conclusion arises. For universally, that quality which is attributed to many different things so as to be assigned to one through the medium of another, abounds most in that medium by which it is transmitted to the rest.
Thus the sun, through the medium of the moon, illuminates the earth by night; thus the father loves the[xlii] preceptor through the medium of his child. And in the first instance the moon is more lucid than any object it enlightens: in the second, the child possesses more of the father’s regard than his preceptor. If then we assent to the conclusions through our belief of the principles alone, it is necessary that the principles should be more known, and inherit a greater degree of our assent. Hence, if it be true that the principles are more known than the conclusions, it follows, that either our knowledge of them is derived from demonstration, or that it is superior to any demonstrative proof; and after this manner we must conceive of those general self-evident notions which, on account of their indemonstrable certainty, are deservedly placed at the top of all human science.
These propositions not only possess greater credibility than their conclusions, they likewise inherit this property as an accession to their dignity and importance; that no contrary propositions deserve greater belief; for if you give no more assent to any principle than to its contrary, neither can you give more credit to the conclusion deduced from that principle than to its opposite. Were this the case, the doctrine of these propositions would immediately lose its invariable certainty.
7. There are, indeed, some who, from erroneously applying what we have rightly determined, endeavour to take away the possibility of demonstration. From the preceding doctrine it appears that the principles are more aptly known than the conclusions. This is not evident to some, who think nothing can be known by us without a demonstrative process; and consequently believe that the most simple principles must derive all their credit from the light of demonstration.
[xliii]
But if it be necessary that all assumptions should be demonstrated by others, and these again by others; either the enquiry must be continued to infinity, (but infinity can never be absolved), or if, wearied by the immense process, you at length stop, you must doubtless leave those propositions unknown, whose demonstration was declined through the fatigue of investigation. But how can science be derived from unknown principles? For he who is ignorant of the principles, cannot understand the conclusions which flow from these as their proper source, unless from an hypothesis or supposition of their reality.
This argument of the sophists is, indeed, so far true, that he who does not understand that which is first in the order of demonstration, must remain ignorant of that which is last:—But in this it fails, that all knowledge is demonstrative; since this is an assertion no less ridiculous than to maintain that nothing can be known. For as it is manifest that some things derive their credit and support from others, it is equally obvious that many, by their intrinsic excellence, possess indubitable certainty and truth; and command our immediate assent as soon as proposed. They inherit, indeed, a higher degree of evidence than those we assent to by the confirmation of others; and these are the first principles of demonstration: propositions indisputable, immediate, and perspicuous by that native lustre they always possess. By means of these, we advance from proposition to proposition, and from syllogism to syllogism, till we arrive at the most complicated and important conclusions. Others, willing to decline this infinite progression, defend the necessity of a circular or reciprocal demonstration. But this is nothing more than to build error upon error, in order to attain the truth; an attempt no less ridiculous than that of the giants of old. For since, as we shall hereafter[xliv] accurately prove, demonstration ought to consist from that which is first, and most known; and since it is impossible that the same thing should be to itself both prior and posterior: hence we infer the absurdity of circular demonstration; or those syllogisms in which the conclusions are alternately substituted as principles, and the principles as conclusions. It may, indeed, happen, that the same thing may be both prior and posterior to the same; but not at one and the same time, nor according to the same mode of existence. Thus, what is prior in the order of our conceptions, is posterior in the order of nature; and what is first in the arrangement of things, is last in the progressions of human understanding. But demonstration always desires that first which is prior in the order and constitution of nature. But the folly of such a method will more plainly appear from considering its result: let us suppose every a is b, and every b is c; hence we justly infer, that every a is c. In like manner, if we prove that every a is b, and by a circular demonstration, that every b is a, the consequence from the preceding is no other than that every a is a; and thus the conclusion terminates in that from which it first began; a deduction equally useless and ridiculous. However, admitting that, in the first figure, circular demonstration may be in some cases adopted, yet this can but seldom happen from the paucity of reciprocal terms.
But that reciprocal terms are very few, is plain from hence: let any species be assumed, as man; whatever is the predicate of man, is either constitutive of his essence, or expressive of some accident belonging to his nature. The superior genera and differences compose his essence, among which no equal predicate can be assigned reciprocable with man, except the ultimate differences which cannot be otherwise than one, i. e., risibility, which mutually reciprocates[xlv] with its subject; since every man is risible, and whatever is risible is man. Of accidents some are common, others peculiar; and the common are far more in number than the peculiar; consequently the predicates which reciprocate with man, are much fewer than those which do not reciprocate.
8. It is now necessary to enumerate the questions pertaining to demonstration; and for this purpose, we shall begin with propositions, since from these, syllogisms are formed; and since every proposition consists of a subject and predicate, the modes of predication must be considered, and these are three which I call total, essential, and universal; a total predication takes place when that which is affirmed or denied of one individual is affirmed or denied of every individual comprehended under the same common species.
Thus, animal is predicated of every man, and it has this farther property besides, that of whatever subject it is true to affirm man, it is at the same time true to affirm animal.
Those things are said to be essentially predicated; first, when the predicate is not only total, but constitutes the essence of the subject; instances of this kind are, animal of man; tree of the plantain; a line of a triangle; for a triangle is that which is contained under three right-lines. But here we must observe, that not every total predicate is an essential one; thus, whiteness is predicated of every swan, because it is inherent in every swan, and at every instant of time; but because whiteness does not constitute the essence of a swan, it is not essentially predicated; and this, first, is one of the modes of essential predication of the greatest importance in demonstration. The second mode is of accidents, in the definition of which their common[xlvi] subject is applied: thus, a line is essentially inherent in rectitude, because in its geometrical definition, a line is adopted; for rectitude is no other than a measure, equally extended between the points of a line. In the same manner, imparity is contained in number; for what is that which is odd, but a number divided into unequal parts? Thus, virtues are resident in the soul, because, in their definition, either some part of the soul, or some one of its powers, is always applied. The third mode of essential predicates pertains to accidents which are inseparably contained in some particular subject, so as to exclude a prior existence in any other subject; such as colour in superficies. The fourth mode is of things neither contained in another, nor predicated of others; and such are all individuals, as Callias, Socrates, Plato. Causes are likewise said to exist substantially, which operate neither from accident nor fortune.
Thus, digging up the ground for the purposes of agriculture, may be the cause of discovering a treasure, but it is only an accidental one. But the death of Socrates, in despite of vigilance, is not the result of a fortuitous cause, but of an essential one, viz. the operation of poison.
9. These posterior significations of essential predicates are added more for the sake of ornament than use; but the two former have a necessary existence, since they cannot but exist in the definition of names which predicate the essence of a thing, and in subjects which are so entirely the support of accidents, that they are always applied in their definition. But it is a doubt with some, whether those accidents are necessary, which cannot be defined independent of their common subject? To this we answer, that no such accident can, from its nature, be contained in every individual of any species; for curvature is not contained in[xlvii] every line; nor imparity in every number; from whence we infer, that neither is curvature necessarily existent in a line, nor parity in number. The truth of this is evident from considering these accidents abstracted from their subjects; for then we shall perceive that a line may exist without curvature, and number without imparity.
Again, I call that an universal predicate, which is predicated of a subject totally and essentially, and considered as primarily and inseparably inherent in that subject: for it does not follow that a predicate, which is total, should be immediately universal; for whiteness is affirmed of every swan, and blackness of every crow, yet neither universally. In like manner, a substantial predicate is not consequently an universal one; for the third mode of essential predicates, and the two following (instanced before) cannot be universal. Thus, colour, although inherent in superficies essentially, is not inherent in every superficies, and consequently not universally. Thus again, Socrates, Callias, and Plato, though they exist essentially, are not universals, but particulars; and thus, lastly, the drinking of poison was an essential cause of the death of Socrates, but not an universal one, because Socrates might have died by other means than poison. If then, we wish to render an accurate definition of an universal predicate, we must not only say it is total and essential, but that it is primarily present to its subject and no other. Thus, the possession of angles equal to two right, primarily belongs to a triangle; for this assertion is essentially predicated of triangle, and is inherent in every triangle. This property, therefore, is not universally in figure, because it is not the property of every figure, not of a square, for instance; nor as universal in a scalene triangle: for although it is contained in every scalene, and in every equilateral, and isosceles[xlviii] triangle, yet it is not primarily contained in them, but in triangle itself; because these several figures inherit this property, not from the particular species to which they belong, but from the common genus triangle. And thus much concerning total, essential, and universal predicates.
10. Concerning that which is universal, we are frequently liable to err; often from a belief that our demonstration is universal, when it is only particular; and frequently from supposing it particular when it is, on the contrary, universal. There are three causes of this mistake; the first, when we demonstrate any particular property of that which is singular and individual, as the sun, the earth, or the world. For since there is but one sun, one earth, and one world, when we demonstrate that the orb of the earth possesses the middle place, or that the heavens revolve, we do not then appear to demonstrate that which is universal.
To this we answer: when we demonstrate an eclipse of the sun to arise from the opposition of the moon, we do not consider the sun as one particular luminary, but we deduce this consequence as if many other suns existed besides the present.
Just as if there were but one species of triangles existed; for instance, the isosceles; the equality of its angles at the base would not be considered in the demonstration of the equality of all its angles to two right ones: but its triangularity would be essential, supposing every species of triangles but the isosceles extinct, and no other the subject of this affection. So when we prove that the sun is greater than the earth, our proof does not arise from considering it as this particular sun alone, but as sun in general; and by applying our reasoning to every sun, if thousands besides the present should enlighten the world. This will appear[xlix] still more evident, if we consider that such conclusions must be universal, as they are the result of an induction of particulars: thus, he who demonstrates that an eclipse of the sun arises from the opposition of the moon between the sun and earth, must previously collect, by induction, that when any luminous body is placed in a right-line with any two others opaque, the lucid body shall be prevented, in a greater or less degree, from enlightening the last of these bodies, by the intervention of the second; and by extending this reasoning to the sun and earth, the syllogism will run thus:
Every lucid body placed in a right-line with two others opaque, will be eclipsed in respect of the last by the intervention of the second;
The sun, or every sun, is a luminous body with these conditions;
And consequently the sun, and so every sun, will be eclipsed to the earth by the opposition of the moon.
Hence, in cases of this kind, we must ever remember, that we demonstrate no property of them as singulars, but as that universal conceived by the abstraction of the mind.
Another cause of deception arises, when many different species agree in one ratio or analogy, yet that in which they agree is nameless. Thus number, magnitude, and time, differ by the diversities of species; but agree in this, that as any four comparable numbers correspond in their proportions to each other, so that as the first is to the second, so is the third to the fourth; or alternately, as the first to the third; so is the second to the fourth: in a similar manner, four magnitudes, or four times, accord in their mutual analogies and proportions. Hence, alternate proportion may be attributed to lines as they are lines, to numbers as they are numbers, and afterwards to times and[l] to bodies, as the demonstration of these is usually separate and singular; when the same property might be proved of all these by one comprehensive demonstration, if the common name of their genus could be obtained: but since this is wanting, and the species are different, we are obliged to consider them separately and apart; and as we are now speaking of that universal demonstration which is properly one, as arising from one first subject; hence none of these obtain an universal demonstration, because this affection of alternate proportion is not restricted to numbers or lines, considered in themselves, but to that common something which is supposed to embrace all these, and is destitute of a proper name. Thus too we may happen to be deceived, should we attempt to prove the equality of three angles to two right, separately, of a scalene, an isosceles, and an equilateral triangle, only with this difference, that in the latter case the deception is not so easy as in the former; since here the name triangle, expressive of their common genus, is assigned. A third cause of error arises from believing that to demonstrate any property inherent after some particular manner in the whole of a thing, is to demonstrate that property universally inherent. Thus, geometry proves[23] that if a right-line falling upon two right-lines makes the outward angle with the one line a right-angle, and the inward and opposite angle with the other a right one, those two right-lines shall be parallel, or never meet, though infinitely extended. This property agrees to all lines which make right-angles: but they are not primarily equidistant on this account, since, if they do not each make a right-angle, but the two conjointly are equal to two right, they may still be proved equidistant. This latter demonstration, then, is primarily and universally conceived; the other,[li] which always supposes the opposite angles right ones, does not conclude universally; though it concludes totally of all lines with such conditions: the one may be said to conclude of a greater all; the other of a lesser. It is this greater all which the mind embraces when it assents to any self-evident truth; or to any of the propositions of Euclid. But by what method may we discover whether our demonstration is of this greater or lesser all? We answer, that general affection which constitutes universal demonstration is always present to that subject, which when taken away, the predicate is immediately destroyed, because the first of all its inherent properties.
Thus, for instance, some particular sensible triangle possesses these properties:—it consists of brass; it is scalene; it is a triangle. The query is, by which of these we have just now enumerated, this affection of possessing angles equal to two right is predicated of the triangle? Take away the brass, do you by this means destroy the equality of its angles to two right ones? Certainly not:—take away its scalenity, yet this general affection remains: lastly, take away its triangularity, and then you necessarily destroy the predicate; for no longer can this property remain, if it ceases to be a triangle.
But perhaps some may object from this reasoning, such a general affection extends to figure, superficies, and extremities, since, if any of these are taken away, the equality of its angles to two right can no longer remain. It is true, indeed, that by a separation of figure, superficies, and terms, from a body, you destroy all the modes and circumstances of its being; yet not because these are taken away, but because the triangle, by the separation of these, is necessarily destroyed; for if the triangle could still be preserved without figure, superficies, and terms, though these[lii] were taken away it would still retain angles equal to two right; but this is impossible. And if all these remain, and triangle is taken away, this affection no longer remains. Hence the possession of this equality of three angles to two right, is primarily and universally inherent in triangle, since it is not abolished by the abolition of the rest:——such as to consist of brass; to be scalene, or the like. Neither does it derive its being from the existence of the rest alone; as figure, superficies, terms; since it is not every figure which possesses this property, as is evident in such as are quadrangular, or multangular. And thus it is preserved by the preservation of triangle, it is destroyed by its destruction.
11. From the principles already established, it is plain that demonstration must consist of such propositions as are universal and necessary. That they must be universal, is evident from the preceding; and that they must be necessary, we gather probably from hence; that in the subversion of any demonstration we use no other arguments than the want of necessary existence in the principles.
We collect their necessity demonstratively, thus; he who does not know a thing by the proper cause of its existence, cannot possess science of that thing; but he who collects a necessary conclusion from a medium not necessary, does not know it by the proper cause of its existence, and therefore he has no proper science concerning it. Thus, if the necessary conclusion c is a, be demonstrated by the medium B, not necessary; such a medium is not the cause of the conclusion; for since the medium does not exist necessarily, it may be supposed not to exist; and at the time when it no longer exists, the conclusion remains in full force; because, since necessary, it is eternal. But an effect cannot exist without a cause of its existence; and[liii] hence such a medium can never be the cause of such a conclusion. Again, since in all science there are three things, with whose preservation the duration of knowledge is connected; and these are, first, he who possesses science; secondly, the thing known; and thirdly, the reason by which it is known; while these endure, science can never be blotted from the mind, but on the contrary, if science be ever lost, it is necessary some of these three must be destroyed.
If then you infer that the science of a necessary conclusion may be obtained from a medium not necessary, suppose this medium, since capable of extinction, to be destroyed; then the conclusion, since necessary, shall remain; but will be no longer the object of knowledge, since it is supposed to be known by that medium which is now extinct. Hence, science is lost, though none of the preceding three are taken away; but this is absurd, and contrary to the principles we have just established. The thing known remains; for the conclusion, since necessary, cannot be destroyed;—he who knows still remains, since neither dead, nor forgetful of the conclusion:—lastly, the demonstration by which it was known, still survives in the mind; and hence we collect, that if science be no more after the corruption of the medium, neither was it science by that medium before its corruption; for if science was ever obtained through such a medium, it could not be lost while these three are preserved. The science, therefore, of a necessary conclusion can never be obtained by a medium which is not necessary.
12. From hence it is manifest, that demonstrations cannot emigrate from one genus to another; or by such a translation be compared with one another. Such as, for instance, the demonstrations of geometry with those of arithmetic. To be convinced of this, we must rise a little[liv] higher in our speculations, and attentively consider the properties of demonstration: one of which is, that predicate which is always found in the conclusion, and which affirms or denies the existence of its subject: another is, those axioms or first principles by whose universal embrace demonstration is fortified; and from whose original light it derives all its lustre. The third is the subject genus, and that nature of which the affections and essential properties are predicated; such as magnitude and number. In these subjects we must examine when, and in what manner a transition in demonstrations from genus to genus may be allowed. First, it is evident, that when the genera are altogether separate and discordant, as in arithmetic and geometry, then the demonstrations of the one cannot be referred to the other. Thus, it is impossible that arithmetical proofs can ever be accommodated with propriety to the accidents of magnitudes: but when the genera, as it were, communicate, and the one is contained under the other, then the one may transfer the principles of the other to its own convenience. Thus, optics unites in amicable compact with geometry, which defines all its suppositions; such as lines that are right, angles acute, lines equilateral, and the like. The same order may be perceived between arithmetic and music: thus, the double, sesquialter, and the like, are transferred from arithmetic, from which they take their rise, and are applied to the measures of harmony.
Thus, medicine frequently derives its proofs from nature, because the human body, with which it is conversant, is comprehended under natural body. From hence it follows, that the geometrician cannot, by any geometrical reasons demonstrate any truth, abstracted from lines, superficies, and solids; such as, that of contraries there is the same[lv] science; or that contraries follow each other; nor yet such as have an existence in lines and superficies, but not an essential one, in the sense previously explained.
Of this kind is the question, whether a right-line is the most beautiful of lines? or whether it is more opposed to a line perfectly orbicular, or to an arch only. For the consideration of beauty, and the opposition of contraries, does not belong to geometry, but is alone the province of metaphysics, or the first philosophy.
But a question here occurs, If it be requisite that the propositions which constitute demonstration should be peculiar to the science they establish, after what manner are we to admit in demonstration those axioms which are conceived in the most common and general terms; such as, if from equal things you take away equals, the remainders shall be equal:——as likewise, of every thing that exists, either affirmation or negation is true? The solution is this: such principles, though common, yet when applied to any particular science for the purposes of demonstration, must be used with a certain limitation. Thus the geometrician applies that general principle, if from equal things, &c. not simply, but with a restriction to magnitudes; and the arithmetician universally to numbers.
Thus too, that other general proposition:——of every thing, affirmation or negation is true; is subservient to every art, but not without accommodation to the particular science it is used by. Thus number is or is not, and so of others. It is not then alone sufficient in demonstration that its propositions are true, nor that they are immediate, or such as inherit an evidence more illustrious than the certainty of proof; but, besides all these, it is necessary they should be made peculiar by a limitation of their comprehensive nature to some particular subject. It is on this[lvi] account that no one esteems the quadrature of Bryso[24], a geometrical demonstration, since he uses a principle which,[lvii] although true, is entirely common. Previous to his demonstration he supposes two squares described, the one[lviii] circumscribing the circle, which will be consequently greater; the other inscribed, which will be consequently less than the given circle. Hence, because the circle is a medium between the two given squares, let a mean square be found between them, which is easily done from the principles of geometry; this mean square, Bryso affirms, shall be equal to the given circle. In order to prove this, he reasons after the following manner: those things which compared with others without any respect, are either at the same time greater, or at the same time less, are equal among themselves: the circle and the mean square are, at the same time, greater than the internal, and at the same time less than the external square; therefore they are[lix] equal among themselves. This demonstration can never produce science, because it is built only on one common principle, which may with equal propriety be applied to numbers in arithmetic, and to times in natural science. It[lx] is defective, therefore, because it assumes no principle peculiar to the nature of the circle alone, but such a one as is common to quantity in general.
13. It is likewise evident, that if the propositions be universal, from which the demonstrative syllogism consists, the conclusion must necessarily be eternal. For necessary propositions are eternal; but from things necessary and eternal, necessary and eternal truth must arise. There is no demonstration, therefore, of corruptible natures, nor any science absolutely, but only by accident; because it is not founded on that which is universal. For what confirmation can there be of a conclusion, whose subject is dissoluble, and whose predicate is neither always, nor simply, but only partially inherent? But as there can be no demonstration, so likewise there can be no definition of corruptible natures; because definition is either the principle of demonstration, or demonstration differing in the position of terms, or it is a certain conclusion of demonstration. It is the beginning of demonstration, when it is either assumed for an immediate proposition, or for a term in the proposition; as if any one should prove that man is risible, because he is a rational animal. And it alone differs in position from demonstration, as often as the definition is such as contains the cause of its subjects existence. As the following: an eclipse of the sun is a concealment of its light, through the interposition of the moon between that luminary and the earth. For the order of this definition being a little changed, passes into a demonstration; thus,
The moon is subjected and opposed to the sun:
That which is subjected and opposed, conceals:
The moon, therefore, being subjected and opposed, conceals the sun.
But that definition is the conclusion of demonstration,[lxi] which extends to the material cause; as in the preceding instance, the conclusion affirming that the subjection and opposition of the moon conceals the sun, is a definition of an eclipse including the material cause.
Again, we have already proved that all demonstration consists of such principles as are prior in the nature of things; and from hence we infer, that it is the business of no science to prove its own principles, since they can no longer be called principles if they require confirmation from any thing prior to themselves; for, admitting this as necessary, an infinite series of proofs must ensue. On the contrary, if this be not necessary, but things most known and evident are admitted, these must be constituted the principles of science. He who possesses a knowledge of these, and applies them as mediums of demonstration, is better skilled in science, than he who knows only posterior or mediate propositions, and demonstrates from posterior principles. But here a doubt arises whether the first principles of geometry, arithmetic, music, and of other arts, can ever be demonstrated? Or shall we allow they are capable of proof, not by that particular science which applies them as principles or causes of its conclusions? If so, this will be the office of some superior science,—which can be no other than the first philosophy, to whose charge the task is committed; and whose universal embrace circumscribes the whole circle of science, in the same manner as arithmetic comprehends music, or geometry optics.—This is no other than that celebrated wisdom which merits the appellation of science in a more simple, as well as in a more eminent degree than others: not, indeed, that all causes are within its reach, but such only as are the principal and the best, because no cause superior to them can ever be found. Hence the difficulty of knowing whether we possess science or[lxii] not, from the difficulty of understanding whether it is founded on peculiar or common principles; since it is necessary that both these should be applied in the constitution of all real knowledge and science.
[25]Again, axioms differ from postulates in this:—they demand our assent without any previous solicitation, from the illustrious certainty they possess. Their truth may, indeed, be denied by external speech, but never from internal connection. He who denies that equal things shall remain from the subtraction of equal, dissents, as Euripides says, with his tongue, and not with his heart. But demonstration depends not on external speech, but on intellectual and internal conviction; and hence, axioms derive all their authority from intrinsic approbation, and not from public proclaim. For the prompt decisions of the tongue are frequently dissonant from the sentiments concealed in the secret recesses of the heart. Thus the [26]geometrician does not speculate those lines which are the objects of corporeal[lxiii] sight, but such as are exhibited by mental conception, and of which the delineations on paper, or in the dust, are no more than imperfect copies, notes, and resemblances. Thus, when he draws a pedal line which is not pedal, or an equilateral triangle which is not equilateral, we must pay no regard to the designations of the pen, but solely attend to the intellection of the mind; for the property demonstrated of some particular line, is in the conclusion applied to one that is universal, and this true line could be no otherwise signified to the learner than by a material description.
The certainty of axioms is, indeed, in a measure obvious to every one. For what more evident than that nothing exists of which it is possible, at the same time, to affirm and deny any circumstance of being? Indeed, so illustrious and indubitable is the light of this axiom, that in any demonstration we are ashamed to assign it the place of an assumption. It would almost seem prolix and superfluous, since there is nothing more manifest and certain; and yet there are cases in which it is necessary to rank it among assumptions. And these take place whenever the intention is to conclude the existence of something as true, and of its opposite as false. Thus, for instance, in the demonstration that the world is finite, we assume this principle, and then reason as follows:
Bound and infinite cannot be at the same time affirmed and denied of any body:
The world is a body:
Therefore the world is not at the same time finite and infinite.
And in this genus of demonstration, the major proposition ought always to assimilate with the conclusion. But the above axiom is not the only one obvious, for the following[lxiv] possesses equal certainty; that of every thing which exists, either affirmation or negation is true. This axiom is of great use in demonstrations leading to an absurdity; for he who demonstrates the impossibility of any opposite assertion, necessarily establishes his own. Hence it is we affirm that the diameter of a square is either commensurable or incommensurable with its side; and this general principle is accommodated, and, as it were, descends into its proper matter as often as that which it possesses of universal is contracted to a certain genus; for, as we have previously observed, common principles are not admitted in demonstration without any restriction; but then only when their general nature is limited to some particular subject, by which they become peculiar and apposite.
14. [27]Wisdom, or the first philosophy and logic, agree in not using axioms after the same manner as other arts; but on the contrary, they confirm and establish their certainty, though with this difference, that the logician reasons only from probabilities, but the metaphysician from the highest certainty and evidence. Besides, we do not[lxv] rank logic in the order of the sciences, because it is destitute of some determinate genus or subject, as it is neither conversant about lines, nor numbers, nor proportions. And its chief concern is about apparent properties, and not such as are essential to a subject.
Hence, in logical disquisitions, we confidently employ interrogations, as equally subservient to the affirmation or negation of an opinion:—a method utterly impracticable, if we only employed those principles which are universally acknowledged; since it is impossible of the same thing to prove contrary properties,—as of the soul, that it is mortal and immortal; but he who demonstrates, assumes one definite part of a question, because his purpose is not to interrogate, but to trace out the latent paths of truth. And hence, if any one affirms that the soul is moved, and immediately after denies it, he is no longer a subject worthy the exercise of our discursive and reasoning powers.
Again, it may so happen, that the same science at one time considers why a thing is, at another only explains its existence, or that it exists, without considering the cause. Thus, the syllogism which concludes by mediate propositions, demonstrates without assigning the proper cause: but that which determines by immediate ones, in a great measure explains the cause or reason of existence. Thus, he who infers that trees do not breathe because they are not animals, reasons from a mediate and secondary cause, because there are many animals, such as insects, which exist without breathing: but he who infers this from their want of lungs, demonstrates from the immediate and primary cause.
Thus, the following syllogism is a mediate one, or such as requires one or more mediums to establish its certainty:
Every thing that is not an animal does not breathe;
A tree is not an animal;
Therefore a tree does not breathe.
[lxvi]
Here the major proposition is evidently mediate, because we are still to seek why that which is not an animal does not breathe, which the following immediate syllogism solves.
Every thing that is not endued with lungs does not breathe;
Every thing that is not an animal is not endued with lungs; ergo,
Every thing that is not an animal does not breathe.
Again, the same science may demonstrate the existence of a thing, or that it exists, and the cause of such existence as often as it assigns two immediate reasons; but the one from the proper cause, the other only from a sign. Thus, he who demonstrates the increase of the moon, from the plenitude of her orb, infers the cause of such increase; but on the contrary, he who collects the plenitude of her orb from her increase, reasons only from a sign, and can alone declare its existence. And, indeed, it often happens that the cause and sign reciprocate, so that as from the sign we advance to the cause, demonstration from the cause frequently recurs to the sign. Thus, from the breadth and firmness of the basis, we collect the permanent duration of the pyramid; and from its extended existence we infer the strength of its support. Whenever, then, the argument originates from a sign, it gives evidence to the conclusion, as from something more known than its cause. When it begins from the cause, it proceeds from that which is first in the order of nature, to that which is last, and reasons as from the proper principle of the thing.
Sometimes the cause and sign do not reciprocate. Thus, although wherever there is smoke, we infer the existence of fire; yet we cannot infer, that wherever there is fire smoke exists. Thus, from the palace and the picture we collect the existence of the architect and painter; but the last may exist without the first;—the living architect without[lxvii] the actual palace; and the living painter without the energies of his art. And thus it is that the cause is illustrated by its sign; but not always the sign by its cause.
Hence then, as all causes do not reciprocate with their effects; so neither is it always causes and effects which do reciprocate: because a multitude of signs, mutually inferring each other, may accompany a certain cause. Thus, the signs which attend the causes of a fever, are a quick pulsation of the artery, and an intense heat: and these signs mutually assert each other; but no syllogism can be composed from either expressing the why, but only simply that the other exists.
15. We now propose to consider the mode in which the two preceding demonstrations are distributed in different sciences. When sciences then are so related, that the one is dependent on the other, as optics on geometry, navigation on astronomy, and music composed by the arbitration of the ear, on that which consists in the knowledge of mathematical proportions: in this case, the demonstration of simple existence, or that they exist, pertains to the science of sensibles; but the demonstration why they exist to the science which is speculative and mathematical.
Thus the mathematician speculates the causes of a certain sensible effect, without considering its actual existence; for the contemplation of universals excludes the knowledge of particulars; and he whose intellectual eye is fixed on that which is general and comprehensive, will think but little of that which is sensible and singular. Thus, by mathematics we may learn the responsive harmony of the last chord, and its consonance with the mean; but we cannot perceive this concord, if unaccustomed to the practice of the musical art. In fine, those sciences which are more of a mathematical nature, I mean such as are more amply[lxviii] conversant with the inspection of things, considering their forms abstracted from every material subject, always demonstrate the why; and such is geometry in respect of optics. Thus geometry considers only such things as are peculiar to right-lines, independent of every sensible connection. For the geometrician does not investigate a right-line as contained in stone or brass; but considers it as entirely detached and unconnected with any object of sense.
On the contrary, optics receives a right-line just as it is perceived in a rule, or engraved in brass. And, indeed, in treating of some particulars, natural science has the same relation to optics, as optics to geometry. Thus, in considering the reason of the appearance of the rainbow, the natural philosopher defines the bow to be an image refracted from a certain cloud against the sun; but why it is endued with such a form, and seen with such a colour, must be assigned by him who is skilled in optics. There are, again, sciences, one of which is not subordinate to the other, because founded on principles totally different; yet, in some particulars they agree with the preceding. Thus, to know that an orbicular wound is the most difficult of cure, belongs to the physician; but to know why, to the geometrician.
16. Of all syllogistic figures, the first is the best adapted to science, since the arithmetician, geometrician, and lastly all those who demonstrate any effect from its proper cause, fabricate their reasonings according to this figure. For the middle figure is seldom used, because only adapted to a few occasions: and since the knowledge of the why is of all others the most important, which is alone obtained by this figure: hence, in the pursuit of science, it is always preferred before the rest. Besides, it is equally accommodated to the knowledge of final causes; to which it alone[lxix] tends: for it composes definitions from words universal, and affirmative. In the second figure, a complex negative is conceived; and in the last, a particular one. Add to this, that mediate propositions are no other ways reducible to immediate ones than by this figure, in which the mediate proposition tends, by a continued series, to that which is immediate. But the second does not conclude affirmatively, nor the last universally; from whence it appears, that a mediate proposition can never become immediate by these figures: not that all affirmative propositions are immediate ones, since some negatives are of this kind; for all propositions are equally immediate, which cannot be confirmed by syllogism; and such are those negatives, of whose terms it is impossible any genus can be affirmed. Thus the proposition, no substance is quality, is an immediate negative of this kind, whose terms are two of the most universal genera of things.
Again, as we have frequently affirmed that he who demonstrates, always assumes such things as are essentially predicated; but that he who argues dialectically or topically, not always, but generally assumes such as are accidentally predicated, and which appear more probable and known than such as are essentially inherent; it is proper we should define what is meant by accidental predication; or something predicated by means of another. Indeed, the term has a diffuse signification: for, first, a body is said to be white by something else, because by its superficies; and in this manner vines are white, because their branches are white. Thus, if accident be predicated of accident, it is by means of another; as when we say the musician is fair; for the being a musician is an accident of man, and the being fair of the musician: and man is the subject of each. The predicate of substance is equally accidental, when not[lxx] included in the number of things substantially inherent; as when we affirm of any particular man that he is red, or black. But the predication is especially accidental, as often as, by perverting the order of nature, substance is predicated of accident; as when we say something white is an animal: for this assertion differs from that other, animal is white. In the latter, the subject animal is neither inherent in another, nor subsists by another, but has an essential existence. In the former, what is assumed as a subject derives its existence from that of which it is the accident. It is only dialectically, therefore, that we can argue from predicates as probable and known without any distinction: but in demonstration, all that are preposterous and accidental must be carefully avoided, excepting such accidents as being essentially in a subject, admit of an essential predication; and some of these we have enumerated before.
17. We are now entering on a disquisition neither ignoble nor useless: it is this, whether the number of things predicated essentially of a subject is finite, or whether things in a continued series run on to infinity. For instance, let us suppose some ultimate subject, which is not the predicate of any thing besides; and let c represent such a subject, of which b is the first and immediate predicate; and in the same manner d of b, and e of d: the query is, Whether or not this extraction must necessarily stop, or will admit of an immense progression, so that f may be predicated of e, and g of f, and so on infinitely; the power of the predicates, which supplies the common identity, still remaining inexhaustible and undiminished? The second query is this, Supposing some general subject, which we call a, of such a nature as to be no longer the subject of any farther predication, but to be itself the supreme and primary predicate; and supposing that it is immediately[lxxi] inherent in f, and f in e, and e in g, whether or not the process must stop, or extend to infinity, and no subject be found which is not directly predicable of another? There is a remarkable difference in the two considerations; for, in the former we enquire whether any ultimate subject can supply an infinite ascent of predicates; in the latter, whether any first predicate can exist in an infinite descending series of subjects. The third question is, supposing two extremes constituted from a first predicate and last subject, whether it is possible an infinite number of mediums can intervene? And this is no other than to enquire whether demonstrations admit of an infinite progression, so that whatever is assumed in proof of another, must be proved itself? Or whether it is not more agreeable to truth, that there should be some immediate propositions and ultimate terms, whose discovery may give respite to enquiry, and stay the elaborate process of demonstration? The same question occurs in negatives. But that some of these are immediate, the instance lately alledged sufficiently evinces. The solution of this enquiry is not so difficult in subjects which mutually reciprocate; for in these, when the ultimate subject is given, no one can doubt the existence of their primary predicate; nor when the primary predicate is admitted, can there be any doubt of the existence of some ultimate subject. For, in things which mutually reciprocate, whatever is enquired of the one, is immediately questioned of the other; and wherever there is a last subject, there must be a first predicate; for by the conversion of the ultimate subject you effect the primary predicate.
Previous to the discussion of the first question, it is necessary to know that infinite intermediates cannot intervene between two finite terms in an ascending and descending series of predications. I call the series ascending which[lxxii] rises to universals; but descending, which, by a contrary process, stops at particulars. Thus, if any one admits that a is some first predicate, and g some ultimate subject, and should contend, that between these terms there may be infinite mediums, he contradicts himself; since he who begins from a in a descending progression, will never, by this means, arrive at g; and he who departs from g in an ascending series, can never finally rise to a. So that the extremes can be no longer finite, as the hypothesis admitted. Indeed, the absurdity of such a supposition is the same as to contend that between one and ten, an infinity of numbers may exist; which is evidently impossible, because the discrete nature of numbers excludes their actual existence in infinitum, between any finite limits; since they can only become infinite from their actual existence and precedence, and not from any dormant power or capacity they possess: for between any two given numbers there is nothing similar to number in capacity, which can ever become number in energy; as in quantity continuous between any two points there are always parts in capacity, which, whenever a proper agent is at hand, become immediately actual. In like manner, he who admits the terms finite, but believes that the mediums are infinite, asserts what is impossible, since these logical predications are of the same discrete nature with numbers themselves. Thus all the predicates which can exist between Socrates and substance, must exist actually, or not at all; for surely between these two terms, or periods, no predicate in capacity can ever be supposed to subsist. If it be urged, that the capacity of receiving these predicates exists between Socrates and substance, still we reply, it is not that kind of capacity in which these predicates can retain the most shadowy existence; out of which they can ever be called forth into[lxxiii] energy, as from some latent retreat; or into which they can finally retire, when energy is no more. And hence we conclude it impossible that infinite mediums can exist between any finite terms.
18. It now remains that we prove, first, by probable arguments, and then by such as are demonstrative, that the extremes in any series of predications are finite; and that an infinite progression is impossible, not only in substantial predicates, but in such as are accidental. For every thing predicated of another is either essentially or accidentally inherent; and is predicated in a natural or preposterous order. It is predicated according to nature, when accident is declared of substance; contrary to nature, when substance of accident. That essential predicates are finite, appears from hence, because a contrary hypothesis excludes the existence of definition, by admitting that all things are contained in some superior genus, and acknowledge some farther definition; since it is impossible that the definitions of genus can ever be circumscribed, while there is a continual supply of other genera, which can never be known without definition; for thus we shall never obtain either a beginning or an end. But to define all things is not possible, because infinity can never be absolved by the most unwearied progression. Predictions then, of this kind, are always circumscribed by a certain number of terms, which prevent their infinite process, and cause all the strength of demonstration, and all the certainty of human knowledge. The same may be proved in accidents; for such as are predicated of substance, are either predicated as qualities or quantities, as relatives, or as actions and passions; as expressive of some habit, or significant of some place; or as connected with some time. Thus we say the wood is white, the triangle is scalene; whiteness being accidental[lxxiv] to the wood, and scalenity to the triangle. It is therefore certain, that every accident is predicated of substance; and it is no less certain that the predicates of substance are finite, since they are all included in the ten universal genera of things.
19. We have hitherto defended the impossibility of an infinite progression of logical predicates and subjects, in a demonstrative process, by such arguments as are dialectical and common: it now remains that we adopt such as are peculiar and certain. Demonstrations, then, are derived from affections essentially inherent in a subject; and these are either such as take place in definitions of a subject, as multitude and quantity, are essentially predicated of number; or, secondly, accidents which are defined from their subjects, as imparity by number. But the predication cannot, in either case, be extended to infinity. For it is not necessary that in the same manner that imparity is predicated of number, something else, suppose c, should be predicated of imparity; and so imparity be contained in its definition, similar to number in the definition of imparity. For in predications of this kind, the terms are always assumed more contracted than their subject; and at length, by a continued procession, must terminate in an indivisible. Thus, as imparity is more contracted than number, c must be more contracted than imparity. Hence, these predications either finally stop, for the reasons we have assigned; or because whatever is predicated of imparity, is necessarily predicated of number; so that one thing as number would be actually contained in the definition of an infinity of things; and so actual infinity must ensue, which is absurd. Lastly, whatever is said to reside in the terms, must be allowed to reside in the subject; so number must be applied in the definition of every affection;[lxxv] and an infinite number of properties will be essentially inherent in number; and number will inherit infinite definitions. But affections essentially resident in a subject cannot be infinite, because it is necessary they should exist in energy. Thus, imparity cannot exist potentially in number; nor reason in man; nor rotundity in a circle, because wherever these subjects have an actual being, it is necessary these essential attributes should be actually inherent. Again, in the definitions of a subject, an infinite process is impossible, because from such an hypothesis nothing could ever be defined; and thus it appears that neither can demonstrations be infinitely extended, nor every thing admit of demonstration, an opinion we have already noticed in the beginning of this section: for if neither universally, nor in every proposition a middle term can be assumed, but as soon as we arrive at immediate propositions, the labour of investigation is finished, the possibility of demonstrating every thing can no longer be defended; since it is proved above, that by limiting the extremes, an infinite number of mediums is necessarily excluded.
And thus, by taking away infinity from the reasoning art, we have given a support to science, which the most vigorous efforts of subtle sophistry can never finally subvert. We have set bounds to that restless spirit of enquiry which wanders uncontrouled in the mind unenlightened by science, by every where circumscribing its progress within the limits of that which is most particular, and most universal, a first predicate, and an ultimate subject: and finally, by asserting that all the evidence of human knowledge results from the lustre of primary and immediate principles, we have held up a steady and permanent light, ever sufficient to direct our steps through the dark mazes of ignorance and error, into the bright paths of certainty and truth.
[lxxvi]
20. Let us next consider whether universal demonstration is preferable to particular, or not. And first, in favour of particulars we may say that their evidence is more exquisite and certain than that of universals. Thus, the knowledge, from inspection, that Callias is a rational animal, is superior to that acquired by a reasoning process which infers his rationality, because every man is a rational animal. By particular demonstration a thing is known as it is, by universal only in common. Besides, particulars possess some solidity, universals none: and the demonstration of things which have a real existence, is more excellent than that of things which have none. And there are no errors more frequent than those about universals; demonstration considering them as things entirely abstracted from singulars. On the contrary, particulars are usurped by the sight, grasped, as it were, by the hand, and the general subject of every sense; so that concerning these, demonstration affirms nothing false or inconstant. But these reasons, however plausible, are easily confused. And, first, the term essential is more closely connected with universals than particulars. Thus the possession of three angles equal to two right, is an affection more essential to the triangle itself, than to one equilateral or scalene. Add too, that in the demonstration of universals we always infer some property of a subject from its simple existence, or because it is such a subject. Again, many affections are contained in singulars assumed from no particular nature, but from that which is universal; as rationality in Socrates, which is not inferred from his existence as Socrates, but from his existence as man. Farther, that demonstration is the more excellent which is derived from the better cause: but an universal cause is more extended and excellent than a particular one; since the arduous investigation[lxxvii] of the why in any subject is stopt by the arrival at universals. Thus, if we desire to know why the exterior angles of a triangle are equal to four right ones, and it is answered, because the triangle is isosceles; we again ask, But why because isosceles? And if it be replied, because it is a triangle, we may again enquire, But why because a triangle? To which we finally answer, because a triangle is a right-lined figure; and here our enquiry rests at that universal idea which embraces every preceding particular one, and is contained in no other more general and comprehensive than itself. Add too, that the demonstration of particulars is almost the demonstration of infinites; of universals, the demonstration of finites.—We add farther, that demonstration is the best, which furnishes the mind with the most ample knowledge; and this is alone the province of universals. Again, the principles of science become immediate only in proportion as the demonstration becomes universal; and he who knows universals, knows particulars in capacity: but we cannot infer, that he who has the best knowledge of particulars, knows any thing of universals. Lastly, that which is universal, is the province of intellect and reason, particulars are the offspring of sense; and hence we conclude that universal demonstration exceeds particular both in dignity and excellence, and is first in the nature of things, although last in the progressions of the reasoning power.
Again, That affirmative demonstration is superior to negative, appears from hence: the affirmative does not require the assistance of the negative; but the negative cannot exist without the affirmative; on which account, the demonstration composed from negatives alone, is incapable of producing real evidence and conviction. Besides, affirmation exceeds negation both in priority and simplicity of existence.
[lxxviii]
Again, the demonstration which concludes directly, is better than that which confirms a proposition by evincing the absurdity of its contrary. The first proceeding in a regular order, establishes, by a natural deduction, the truth which was first advanced. The second taking a wider circuit, yet with the same intentions produces a conclusion quite opposite to its apparent design. The one may be compared to the open attack of a valiant and skilful soldier, who expects the conquest of his enemy from strength and courage alone: the progress of the other resembles the same soldier, uniting force with stratagem, and advancing, by an irregular march, which his foe mistakes for a retreat, but finds the secret cause of his destruction. The first is simple and impromiscuous, as composed from propositions alone: the second is compound and miscellaneous, calling in hypothesis to its assistance.
21. One science is said to be prior to, and more certain than another in many respects;—when the one reasons from primary causes, but the other from such as are secondary:—when the one may be ranked in the genera of intelligibles and universals; but the other in the genera of sensibles and particulars. And such is the relation of arithmetic to music; of geometry to optics; and lastly, of every superior to every subordinate science. Again, this happens when the one reasons from simple principles, the other from such as are complex and connected; on which account arithmetic seems to possess greater certainty than geometry. For the principle of arithmetic is unity; but of geometry a point; and unity is without position, with which a point is always connected. And in this manner geometry inherits greater evidence than astronomy; for the one considers body simply, the other as connected with a circular motion. The science is called one which contemplates[lxxix] actions belonging to one genus: the genus is one which possesses the same first principles; and hence geometry and stereometry form one science. On the contrary, the sciences are called different which have different principles, such as geometry and optics; the latter of which does not originate from the principles of the former.
Again, the same thing may admit of many demonstrations, and may be known from many mediums: at one time from the application of such as are congenial: at another, from those of a different order or genus. From congenials, as when we demonstrate that the plantain is a substance, first, by the medium of a tree, and then by the medium of a plant, thus:
Every tree is a substance;
The plantain is a tree:
Therefore the plantain is a substance. And again,
Every plant is a substance:
The plantain is a plant:
Therefore the plantain is a substance.
We demonstrate, from mediums, of a following order or genus, as when we prove man to be a substance, at one one time from his being rational, at another from his being a biped; and these mediums, in part, mutually contain each other.
22. Fortuitous events can never, in any science, become the subject of demonstration; since they are neither limited by necessity, nor admit the arrangement of syllogism. Indeed, so far from obtaining a necessary, they do not possess a frequent existence, but every syllogism is composed from one or other of these.
Again, science is not the business of sense, since that which is universal is the object of perception in particulars themselves. For the object of sight is colour in general,[lxxx] and not this particular colour: the object of hearing is sound in general, and not any particular sound; and, on this account we see or hear not only this or that colour or sound, but likewise every other which falls under the cognizance of these senses. Hence, if it were possible for any one to discern by his sight, the equality of the three angles of some particular triangle to two right, he would not by this means possess a demonstration of the conclusion which affirms this to be the property of every triangle; but his knowledge would extend no farther than the triangle he inspects. Thus too, if we could perceive an eclipse of the moon to arise from the interposition of the earth, we could not universally conclude that this is the cause of every eclipse, but only of the particular one we behold. For the explication of causes extends to universals; and comprehends not only the knowledge of one particular defect of the moon, but simply of every eclipse; since the interposition of the earth is not so much the cause of any present eclipse, as of all which can possibly exist in every age. Whenever, then, the cause is universal, the knowledge of any effect deduced from such a cause is, in every respect, superior to the evidence arising from the perceptions of sense. It is likewise more excellent than the apprehension which subsists independent of the proper cause; as if any one should give absolute credit to the proposition, that the three angles of a triangle are equal to two right, without a previous conviction that the external angle of a triangle, is equal to the two interior opposite ones; and without applying this last proposition as the cause of the first. The comprehension, then, which is conjoined with the proper cause, far exceeds the strongest evidence of sense.
But perhaps it may be said that science consists in sense, because the science of any particular, fails from a defect of[lxxxi] the sense by which it is apprehended. To this we reply, that science, indeed, is not acquired without the assistance of sense, but it does not follow from hence, that to perceive is to know; because the object of science is that which is universal; but of sense, that which is particular. Thus, if we could see light penetrating the pores of glass (on the atomical hypothesis) the cause why it illuminates would be manifest from sensible inspection as the means, and from the universal apprehension of science, by which we should understand this to be universally true.
Again, the principles of all sciences cannot be the same neither considered as remote or proximate. Not considered as proximate, because the principles always correspond to the demonstrated conclusions; but these are not the same, since they are often generically different; and consequently the propositions from which they result must be derived from discordant genera. But propositions consist of such things as essentially exist; and hence we infer, that the principles of geometry are essentially distinguished from those of arithmetic, that they cannot admit of reciprocal accommodation, so that the one may be predicated, or become the subject of the other, and that the one can never be subservient as a medium to the other. Again, common and first principles are not applied in every science; such as this, that every thing must either be affirmed or denied. Nor can any thing be proved by their assistance alone, but as often as these are required in demonstration, other principles more proximate and peculiar to the given proposition, must always be adopted. Again, axioms universally conceived, cannot be assumed in syllogism, but they must be contracted, as it were, to some subject genus. Of this kind is that common axiom, that as often as any four quantities are proportionable, by permutation, or changing[lxxxii] the order of the terms, the same ratio will result. For the arts apply this axiom in a restricted sense; geometry, by considering the relatives as four magnitudes, and arithmetic as four numbers; but the natural philosopher, by adapting the comparison to four motions, or four times. Besides, if the principles of all sciences were the same, it is necessary they should be comprehended by some certain number, similar to the limitation of the elements: but every science is capable of immense increase from the many different modes of amplification the conclusions will admit; and consequently it is requisite to establish a correspondent number of proper principles; for such as are common cannot be alone sufficient. Lastly, if the same principles accord with every science, it follows, that any thing may be demonstrated from such principles: but the certainty of geometrical conclusions cannot be established from the principles of music; and from hence it follows, that although the principles of every science are not the same, they do not possess an entire diversity, nor yet an absolute affinity of nature.
23. There is a remarkable difference between science and opinion. Whatever is the subject of science must have a necessary existence; on the contrary, opinion is conversant with things liable to mutation and decay. Again, as science depends on necessary propositions for support; so opinion on such as possess only a possibility of existence; and so there is one mode of approbation in subjects of opinion, and another in those of science. Hence science is distinguished from opinion by two discriminations, the one arising from their subjects, the other from the mode of approbation. That opinion is conversant with things possible or contingent, we may learn from hence; contingencies cannot belong to science, because their existence is[lxxxiii] not necessary; nor to intellect, or that principle of science by which its terms are known; nor to the apprehension or belief of immediate propositions, called indemonstrable science. Hence, if every habit by which truth is known, is either science, or intellect, or opinion, it remains that opinion alone consists of things which are, indeed, true; but not necessary. It is, therefore, inconstant and unstable, from the mutable nature of its subjects. Besides, no one thinks he possesses an opinion of things which he believes to have a necessary existence, so that they cannot be otherwise than they are; but to such conviction he properly gives the name of knowledge, and to its contrary the name of opinion.
Again, the same thing from the same propositions may at one time become the subject of knowledge, at another, of opinion; and this happens according to the different formation of the syllogism which the propositions compose; whether reasoning from the proper cause it explains the why, or only simply declares a thing exists. Hence a doubt arises why opinions of this kind may not be called science, since both the subjects and propositions are the same? The solution is obvious. If it is believed that the propositions cannot be otherwise than they are, or that they have a necessary existence, such an assent of the mind is not opinion, but science; because things which inherit an essential existence are the ornaments of science alone. On the contrary, if we are convinced that the propositions are true, but at the same time not necessary, such conviction is not science, but opinion. Hence, it is impossible that science and opinion can be the same, since they vary in their definition and mode of approbation, and in a different manner demand our belief. Similar to this, although it may happen that of the same thing a true and a false opinion may arise, it[lxxxiv] will not therefore follow, that true and false opinions are the same. For that which is firm and constant can never be the same with that which is mutable and frail; and that which is always true must be essentially different from that which may be changed into false. By the power of habit indeed in different men, the same thing may be comprehended by opinion and science. Thus it was opinion in Epicurus when he said that the sun was eclipsed by the moon passing under its orb, because he thought it might otherwise happen, and that the moon might be interposed without obscuring the light of the sun. It was science in Hipparchus, because he knew it as a necessary event. But in the same mind, at the same time, and of the same thing, it is impossible that science and opinion can exist. And thus much concerning the difference of the two.
24. Lastly, sagacity is an acute and sudden apprehension of the medium, or proper cause of a certain effect: as if any one, beholding the moon, should in a moment conjecture the cause of the part opposite to the sun being lucid, and the other parts obscure, because she derives her splendor from the sun. Hence he is universally called acute and sagacious, who, from the aspect or hearing of the extremes, can readily perceive the medium which exists between them: as the term imports a certain revolution of the conclusion into its first propositions, and, as it were, a swift comprehension and continuation of the medium.
[lxxxv]
In the ensuing Commentaries, the soul is considered as immaterial; and as possessing a middle nature between intelligibles and sensibles; but that this important assertion may not remain without proof, the following demonstrative arguments, derived from the Platonic philosophy, are offered to the reader’s consideration. And first, that the soul is an unextended, and consequently immaterial essence, may be thus proved. If, after the manner of magnitude, it consisted of continuous parts, it would be impossible that any one part could be sentient from the passion of another; but the soul, for instance, which is situated in the finger, would be sensible of passion, as if detached from soul in the other parts of the body, and existing by itself; for the soul, from this hypothesis, would be sentient by parts, and not considered as a whole. Besides, there must be many souls governing each part of us, different among themselves, and endued with their own peculiar energies. For whatever may be said of continuity, is to no purpose, unless it conduces to unity of sensation; so that the hypothesis which supposes that the sensations gradually arrive at the principal part of the soul by a certain continued succession, is not to be admitted, since it may be reasonably asked, How is the principal part to be peculiarly distinguished? By what rule of quantity can the parts be discerned, by what difference are they to be distinguished, where the quantity is one, and the bulk continuous? Besides, is the principal part alone, or are the other parts, sentient? If the principal part alone be perceptive, the soul can then alone be sentient when a sensible passion meets with this principal[lxxxvi] part, situated in its peculiar seat; but if a sensible passion falls upon any other part of the soul destitute of sense, it is impossible that such a part should be able to transmit the same passion to the principal, or be at all sentient. For how can that which is void of sense, receive passion, and convey it entire to a sentient part? Besides, if passion accedes to the principal, it either falls on one of its parts, and so either one part alone will be sentient, and the rest without sensation, and consequently superfluous, or there must be innumerable and dissimilar sensations; for if the sensation of each of the parts singly, is the same with the aggregate of them all, of what use is a multitude of parts? But if the sensations are various, a man may say, as it were, I am primarily sentient in this place, and secondarily in another; and every sentient part besides the first, will be ignorant where sensation is most powerful: or perhaps (from such an hypothesis) every part of the soul will be equally deceived, each part thinking the passion to arise in the place where it is situated. But if not the principal part alone, but every part of the soul be sentient, a principal part is superfluous for the purpose of sensation; and if the soul be divisible like magnitude, how is it able to recognize, as belonging to one subject, the qualities which flow, as it were, through many senses, as through the eyes and ears? For that part of the soul which is perceptive through the eyes, distinguishes nothing but colours; that which energises through the ears, nothing but sounds; and that which acts through the medium of the touch, nothing but the surfaces of bodies: what is it then which perceives all these properties of bodies united in one subject, or what is that which perceives any thing as a certain one? For unless the intentions of the senses, and of sensible objects, were collected together in one, the soul could[lxxxvii] never be able to judge of the peculiar and different properties of bodies: Hence it is necessary that the soul should be, as it were, a general centre; that the several senses should be extended on all sides to this, similar to lines verging from the circumference of a circle to the centre; and that a power of this kind, comprehending all things; should be truly one. For if the soul was any thing divisible, and the intentions of the senses reached the soul, and ended in its essence like the extremities of various lines, they must either again concur in one and the same as a medium, or have different situations, in such a manner that each sense may perceive different from one another: as if, for instance, the sense of sight should perceive the form of Socrates, and the sense of hearing recognize his voice; that essence which pronounces the whole to be one person, that of Socrates, must be something different from each of the senses. Hence it is necessary that the soul should be an indivisible essence; for if she possessed magnitude, she must be divided along with every sensible object she perceives; so that one part of the soul would perceive a certain part of a sensible object, and we should possess no sentient power capable of perceiving the whole, or of pronouncing any thing one. Thus, in the perception of a man, considered as one, how is it possible that the soul can be divided, so that the perception of a part shall be the same with the perception of the whole. But if we suppose the soul divisible in all her perceptions, since it is impossible she should be co-extended with every sentient object, in how many parts is the division to be made? Is the soul to be distributed into the same number of parts as the sensible object she perceives, so that every part of the soul may perceive the same part of the object? Or shall we say that the parts of the soul have no sensation of the parts of the[lxxxviii] object? But this would be absurd and impossible. If every part then of the soul perceived every part of a magnitude as a whole, since magnitude is divisible to infinity, and since, on this hypothesis, there must be innumerable sensations of every sensible object, there must be innumerable images, as it were, of the same thing in our principal part. Besides, if that which perceives is corporeal, it will not be possible for it to perceive in any other manner than as if certain images were impressed from a seal in wax, or in brass, or in any other sensible substance. But if the images of sensation exist as in humid bodies (which is most probable), they will certainly be confounded like images in water; nor can there be any memory, the image departing with its forming substance. And if we suppose the figures to remain like impressions in solid bodies, either it will not be possible for others to succeed while the former endure; and thus, sensations of other things cannot take place; or if others succeed, the former images must be immediately destroyed, and memory be no more. So that if we allow it possible to remember, and, besides this, to perceive other things, without any hindrance from former impressions, it is impossible that the soul should be corporeal. Since the soul, therefore, is an unextended, indivisible, and immaterial substance, it is consequently incorruptible and immortal; for every thing capable of dissolution and dispersion is either corporeal and composite, or exists in some subject from which it is inseparable. And indeed, whatever may be dissolved is corruptible, as being compounded from many. But whatever naturally subsists in something different from itself, when it is separated from its subject, immediately vanishes into non-entity. But the soul, as we have proved, is incorporeal; it is likewise removed from every subject, and naturally reverts to itself, and is therefore immortal and incorruptible.
[lxxxix]
2. Let us now consider how, and on what account the soul is said to be of a middle nature, and to be the receptacle of all middle energies, both vital and gnostic. Since, then, there is a long gradation of beings, proceeding from the first being, even to formless matter, which is nothing more than the dark shadow of essence, it is requisite to enquire what the properties are of the first and last beings, and what the condition is of the middle orders; for thus we shall know where the essence of the soul ought to be placed. The properties of intelligible natures, therefore, are as follows: true being, eternal, indivisible, immoveable, total, perfect, full of essence, replete with life, free, moving all things, similitude, presiding over all things, and at the same time separated from all; for each of these properties appears in intelligibles, according to the processions of being. But the properties of sensible natures, different from these by the greatest interval, are such as, not-true-being, temporal according to essence, partible, moveable, particular, indigent of another, always replete with subsistence, living by participation, moved by another, dissimilitude, and occupying place by parts. But the middle properties of these are, not-true-being, an essence better than non-being, and inferior to true-being, according to essence eternal, but according to its energies extended with time, indivisible according to its divine part, but divisible according to the various processions of reasons, self-motive, governing things moved by another, but subordinate to such as are immoveable, bearing before itself a particular nature, together with its totality; (for, because it contains in itself all reasons, it is after a manner a whole, but because it is diminished and fallen, ends in parts, and suffers a transition of its energy, it must be esteemed a particular nature): and again, perfecting itself, yet, nevertheless,[xc] perfected by natures prior to its own; filling itself with power and strength, and at the same time filled by others: living from itself, and receiving life from others, being more divine, indeed, than things which live only by participation, but inferior to things primarily vital; moving other things, and itself moved by others; at the same time similar and dissimilar; and separated, at the same time, from last natures, and co-ordinated with them. Such then, being the properties of the first, middle, and last orders, let us consider where we ought to place the soul, whether in the first order, or in those which retain the last place: but if we establish it among the first, it must be true being, every way eternal and immoveable, and it must consequently possess every thing which we have attributed to the first beings; add too, that on this hypothesis we can no longer attribute to the soul a power of self-motion, nor the discursive processions of reasoning, nor a variety of other particulars, which manifestly belong to the soul. But can we place it with propriety among the last of beings? The least of all: for on this hypothesis we shall make it alone moved by others, divisible, composite, and alone possessing perfection from others, the opposite of which is evident in all our souls; since they move and perfect themselves, and are led wherever they please. Since then it is not possible to place the soul either in the first, or last order of beings, it is requisite to assign it a middle place, in imitation of its divine cause Rhea (according to the theologists), who is the conciliating band of the two parents Saturn and Jupiter, and is reported, from her prolific bosom to produce the life of the soul. But though the soul is thus the extremity of intelligible, and the principle of sensible natures, we must not conceive it to be such a principle or extremity as a point in a line, for it is not in both the[xci] natures it terminates, like a point in both the sections of a line; but it is to be called the extremity of intelligibles, because it appears after an intelligible essence, and the principle of sensibles, as being abstracted from them, and the source of their motion. And thus it will preserve to us a certain proportion, that as the natures which are moved by others, are to those which are moved by themselves, so are these last to immoveable natures; and hence it will obtain the condition of a bond, on account of its peculiar mediocrity, unfolding, indeed, united causes, but reducing the dissipated powers of sensibles into one, and being contained by an immoveable and perpetually abiding cause; but containing itself the generation, which, moved by another, is subject to continual mutation. It is likewise intelligible, if we regard generated natures; but generated, if we compare it with intelligibles; and thus it exhibits in its middle nature both extremes, imitating also, by this means, (according to the Greek theologists) its divine cause, for it is said to be on both sides refulgent, ἀμφιφαὴς, and to be endued with two faces ἀμφιπρόσωπος, and to receive in its bosom the processions of intelligible natures. It is likewise said to be replenished with intellectual life, and to be the fountain of the ever-running streams of corporeal life, and to contain in itself the centre of the processions of all beings. On this account it is, with great propriety, affirmed to be generated, and at the same time without generation. For true being, according to the Platonists, is without generation, because it has an infinite power of being totally present at the same time: and body is said to be generated, because it always possesses in itself an infinite flowing power, which it cannot at once totally receive. The soul, therefore, because it is incorporeal, abiding in itself, has an infinite power of being, and this total with respect to its[xcii] essence, and immortal without generation; but according to parts it may be considered in infinite production. For it has not the same total infinity ever present, or there would be the same infinity of the whole and part, of the perfect and imperfect, of the contained and containing, which is impossible. But neither is it possible that the whole of its essence should be in the act of perpetual production, any more than that a part of it should be eternal being, lest the part should be more worthy and better than the whole. Hence the ὑπόϛασις, or subsistence of the soul, is at the same time of infinite power, and is generated in infinitum; for by this means it participates of being, and obtains the first place among generated natures; while body alone, both with respect to its whole and parts, is obnoxious to a perpetual generation.
3. But let us now enquire from what genera Plato composes this nature of the soul, which contains in itself the bond of all beings; previous to which it will be requisite to explain what these genera are, and from whence they originate. Of the species, then, existing in the intelligible world, or the divine intellect, which contains in itself the causes of all posterior natures, some are most general, extending themselves to the universality of things; but others are more particular, like the most special species, and others subsisting between these, expand themselves, indeed, to a multitude of things, but not to all, according to the division, of the Elean guest in the Sophista. For man is produced from the ideal man, and horse from the ideal horse, in the intelligible world; but the similitude which is found in man and horse, and other animals, is produced from likeness itself, or the ideal similitude, as dissimilitude from unlikeness itself; but the sameness and difference which are found in all beings, proceed from the sameness and[xciii] difference which subsist in ever-vital energy and perfection, in the supreme intellect, or the ideal world. Now, as among the sciences some are especially universal, so in intelligible causes some are perfectly particular, presiding alone over the proper and peculiar number of one species; but others extend themselves to a multitude, such as equality, likeness, totality, (for the whole considered as a whole is not common to all things, since the part is not a whole); but others, again, expand themselves to all things, as all beings participate of these, considered as beings, and not considered as vital or animated, or possessing any other property exclusive of the denomination of being. Because, therefore, being is the first, the causes of being obtain the most universal order among genera; and these are five in number, as follows, essence, sameness, difference, motion, and station. For every being is endued with essence; is united to itself; is by itself, or its own sameness, separated from others; proceeds from itself, and its own state and principle, and no less appears to participate of a certain abiding, in preserving its own proper species. All things, therefore, whether intelligibles or sensibles, or subsisting between both, depend on these genera for their existence. For without the being of essence, nothing could subsist; in like manner, without sameness every whole would be dissipated, and divided from itself; and difference being taken away, all things would be one alone, and multitude be destroyed. But without motion and station, all things would either be inefficacious and dead, or, losing their proper state and stability, would end in non-entity.
4. Such then being the middle nature of the soul, Plato, with great propriety, in the Phædrus, and in his tenth book of laws, defines it to be number moving itself; which definition he received from Philolaus, and Philolaus from[xciv] Pythagoras. For since mathematical species have a middle subsistence, as is proved in the following Commentaries, they are of all things most accommodated to the nature of the soul. Hence Plato, in imitation of Pythagoras, sometimes explains the soul by number, as in the present instance; and sometimes by figure and magnitude, as in the Timæus; while he considers in the soul the intersection of lines, and a twofold circle. For since mathematical forms are separated from the flux and inconstancy of matter, they participate of a certain, exact, sure, and exquisite condition, by means of which they eminently confer to the elevation of our ingenuity, and the explication of latent concerns; and, on this account, as they pertain to numbers, we may say, preserving the analogy, that there are five orders of numbers, the divine, the essential, the animative, the natural, and the mathematic. The first of these is uniform, the second immoveable, the third self-motive, the fourth moved by another, and the last the image of the others, and their external measure. The divine number is considered eminently in the deity, as in the principle of all things; the essential belongs to intellect through ideas, and is called essence, unity, and the first being; the animative number belongs to the soul, through the medium of her inherent reasons; the natural to physical concerns, through the seeds of nature; and lastly, the mathematical belongs to opinion, as it is nothing more than the image of essential number, formed by the energies of the rational soul. The soul, therefore, is number, not limited by quantity, and mathematical, but animative; it is number, not indeed numbering, but numbered, generating and converted into itself. Hence too, because harmony arises from number, the soul is called harmony; not, indeed, a harmony of the parts of the body, nor the harmonic quantity which[xcv] subsists in sound or in voice; but a harmony arising from its essential numbers, placed in its inherent reasons, and in the genera which constitute its nature. It is this harmony which produces, as from its proper cause, the harmony of the corporeal parts, the rhythm of motions, and the melody of voices and sounds. It is this which produces that delight in the soul from sensible harmony, which sufficiently indicates it to be something familiar and domestic to her nature. From hence it may be inferred, that Plato is not inconsistent with himself when, in the Phædo, he denies, and in the Timæus affirms, the soul to be harmony; for he denies that it is a harmony of a definite quantity, or such as arises from the parts of the body; but he asserts it to be a harmony in the manner already explained. It may likewise be inferred, that Plato is ignorantly accused by a many, for affirming that the soul is harmony, or number; for they only regard vulgar mathematical number, and sensible harmony; while Plato, far more elevated, discourses of intelligible numbers, and ideal harmony, subsisting in immaterial energy and perfection.
5. And here it is necessary to consider what number, in a particular manner belongs to the soul; for various numbers, differently considered, accord with her self-motive nature. In the first place, union and unity may be considered in the soul, as in her proper degree she participates of divine unity; and likewise with relation to her totality, for she is one certain whole. And because a whole may be considered in a triple respect, one before the parts, another rising from the aggregate of parts, and a third subsisting in the single parts; the soul is a whole in each of these respects. Thus she is a whole prior to the parts, while she is considered as divisible into them, in an incorporeal manner; she is a whole rising from parts, while assuming the[xcvi] parts in the first place, we consider how her nature is fabricated from their conjunction; and she is a whole in the single parts, since she is total in the whole, and in every part. Besides, the duad belongs to the soul, because she contains in her nature bound and infinite, sameness and difference; and lastly, a conversion to intelligibles and sensibles. And, indeed, the duad conjoined with unity, very properly accords with the soul; for to intellect above soul, unity particularly belongs; to body beneath soul, the infinite alone; and to soul situated in the middle, duality properly agrees, being, as it were, infinite, connected with unity. Again, the ternary number is attributed to the soul, as well on account of her beginning, middle, and end, as because she abides in herself, proceeds to inferiors, and returns to supernal natures. Besides, she flows from the one, recedes from him, and is reflected into the one when she acquires her proper perfection. Lastly, as Proclus observes, the nature of the soul is divided into essence, power, and energy; so that she may be said to rejoice in the ternary number, and to be replete with its perfection. But the quaternary number belongs to the soul so far as she is connected with matter, which is tempered with four qualities, and four elements; and she is endued with four principal faculties, nutrition, sensation, local motion, and intellection. But to omit other numbers, and their conformity with the soul, the quinary, and septenary numbers are especially attributed to the soul. The quinary, because the soul is composed from the five genera of things, we have previously explained; and because five particulars merit a principal consideration in the soul; first, her essence; secondly, the harmony of her reasons; thirdly, the species arising from the concord of her parts or reasons; fourthly, her virtue; and, lastly, her energies: and on this account,[xcvii] Proclus observes, the consideration of the soul ought to receive a quintuple distribution. Besides, as the soul consists from a divisible and indivisible nature; so the quinary is composed from the first even and the first odd number. Lastly, as the soul is the connecting medium of the universe; so the quinary obtains the middle situation in universal number, that is in the decad. But the septenary number belongs to the soul, because, as Plato shews, in his Timæus, all harmonical reasons are contained in the seven numbers, 1, 2, 3, 4, 9, 8, 27; and from these the soul is composed. Hence Proclus elegantly observes, that the septenary number is dedicated to Apollo, the parent of all harmony; because in one, two, and four, from which the septenary results, the first bisdiapason is found. Besides, the writers on harmony affirm that all the difference of voices proceeds as far as to the seventh degree. So that Plato uses, with great propriety, the septenary number for the composition of the soul. Again, in these numbers of the soul, every medium is found in a convenient proportion; in these the geometric medium is contained, corresponding to the right institution of laws; of which Plato, in his Republic, says, that by this cities are properly governed: there is found too, an harmonical medium, which is the similitude of justice: and lastly, we may discover an arithmetical medium, which is called the illustrious symbol of peace. After this manner, therefore, Plato, with a wonderful fecundity of significations, affirms that the soul is composed from numbers. He likewise considers the figures she contains, I mean the circle and triangle; because as the soul is the first nature which verges to body, so these are the first of all figures, as well rectilinear as curvilinear. Besides, an orbiculation agrees to the soul, through intellect; but progression and rectitude according to her[xcviii] own proper nature; and on this account she contains both a straight and circular figure. I omit other correspondencies of a circle and triangle with the soul, as they are exhibited in the following Commentaries; and particularly by Proclus, in the third book of his Commentaries on the Timæus: it is sufficient to the design of this Dissertation, just to have mentioned this analogy, that the nature of the numbers and figures may appear, which are considered by Plato in the composition of the soul.
6. Let us now pass from contemplating the nature of the soul, to a survey of its various gradations of knowledge, and the means by which it acquires the illuminations of science; as this is a speculation perfectly essential to a full comprehension of the ensuing Commentaries. According to Plato, then, in the sixth and seventh books of his Republic[28], there are four degrees of the internal cognitions of our soul; imagination, or assimilation; faith, cogitation (διάνοια); and lastly, science or wisdom. The two first degrees conjoined constitute opinion; but the two last equally joined produce intelligence in its large acceptation. I say in its large acceptation, because the word intelligence is considered by the Platonists in a triple respect. First, as it rises from opinion and science; as Plato asserts, in the seventh book of his Republic. Secondly, as it passes into the same with science; for thus, in the end of the sixth book, he considers intelligence and science as the same. Lastly, as it is distinguished from science, and intelligible from that which is the object of cognition: thus, science regards the essential reasons of the soul; but intelligence elevates us to ideas, and this is intelligence in its proper acceptation. The distinction of these four degrees, especially depends on the distinction of things with which the[xcix] soul is conversant. For these four degrees of things are, the image of a sensible object, the sensible object itself, the image of an intelligible object, and the intelligible itself. Imagination or assimilation regards the image of the sensible object; which image is nothing more than the shadow or resemblance appearing in water, or other lucid and polished bodies. Faith is conversant with sensible objects; and these are animals, plants, and every thing subject to the energies of sense. From the junction of imagination and faith, opinion is produced. Cogitation is conversant with the image of an intelligible object; which is nothing more than a certain universal, collected from sensibles, related to the reasons of things existing in the soul, and constituted by their assistance; but not elevated to ideas, and resolved into their lucid nature. Those who are conversant with this image of an intelligible object, use hypotheses; which do not elevate us to principles, which are reasons and ideas, but bring us down to subordinate objects. Lastly, science, considered as the same with intelligence, is conversant with that which is intelligible, or the essence of things; and of this kind are reasons pertaining to the soul, and ideas to intellect. Hence, as intelligible is to sensible in splendor and truth, and form to its image; such is the relation of the superior to the inferior degrees of cognition. And as these four degrees may be resolved into five, by separating intelligence from science; so they are reduced by Plato into two principal degrees; so far as the two first are conversant about generation; but the two last about essence. And thus much for the first particular proposed.
It now remains that we investigate the mode in which science is produced in the soul, according to the doctrine of Plato. For this purpose, I think it will be necessary to[c] consider the rational soul, in whose nature all reasons corresponding to ideas, have been inserted from eternity, received into the human body, as into the plain of oblivion; bordering on the river of negligence, that is placed near to the flux of humours; which producing in its nature various kinds of perturbations, are the causes of its self-oblivion and neglect. Hence the soul, thus constituted, as it were, sleeping and intoxicated; sleeping before it is roused; intoxicated before it is purified; begins from external sensible objects to be moved and excited, and to seek with avidity, the knowledge congenial to its nature. The soul now, enquiring after truth and the sciences, is first conversant with the external images of things, in which the glimmering light of similitude to truth, presents itself to the view; then it distinguishes these images among themselves by its reasoning power; and if they agree in any particular, collects them into one. Thus, being employed in separating into many, things united, and reducing many into one, it advances from shade to substance, and is elevated from similitude to truth itself; and thus apprehends the essence of a thing free from every foreign or contrary quality, shining in reason and idea. Afterwards, from this contact, especially salutary to itself, it experiences an ineffable joy, as from a return into its proper nature, and best disposition; and so great is its exultation, that it neglects and despises the shadows which it formerly pursued. Then the soul truly knows, that while a man regards corporeal natures, he is employed in resemblances; and that though he may esteem himself knowing in many things, he knows nothing in reality; but is then alone elevated to the sublime degree of science, when he arrives at ideas. Hence it appears, that there are four subordinate dispositions of mankind in order to science. For, in the first place, children, as new[ci] guests of this world, are ignorant of every thing, without being conscious of their ignorance. But as they advance in years, they are employed in the shadows and images of natural concerns; and not being yet converted to the essences of things, though they possess no real knowledge, yet they conceive themselves to abound in knowledge. But in the third place, being elevated to supernal natures, and judging these to be alone true, they affirm themselves to be ignorant of all they formerly imagined themselves to know; in which degree Socrates professed to find himself, when he said, this one thing I know, that I know nothing; an ignorance preferable to all the knowledge gained by the most unwearied experimental enquiries. Indeed, this order is indicated by Socrates himself, in the Phædo, when he says, that on his first acquaintance with natural concerns, he thought he abounded in knowledge, but as he advanced in these pursuits, he perceived that he knew nothing. Lastly, when, through the piercing sight of the soul, men are elevated to ideas, they become illustrated with the splendors of true science, and pass into the regions of perfect reality. And hence it appears how true science, which is the same with intelligence and wisdom, produces piety and religion: for science elevates us to intellect and divinity; and copulates the soul with natures of the greatest purity and perfection; so that an union of this kind cannot take place without piety, sanctity, and religion; as dissimilars can never be blended in amicable conjunction.
[cii]
We are informed by Proclus, in the ensuing Commentaries, that the end of geometry, and, indeed, of mathematics in general, is to be referred to the energies of intellect; and that it is degraded when made subservient to the common utilities of a mere animal life. But as the very opposite to this is the prevailing opinion of the present age, let us examine the truth of this doctrine, and attend to the arguments which the Platonic philosophy affords in its defence. For if we can prove that this assertion of Proclus is supported by the strongest evidence, we shall vindicate the dignity of true geometry, restore it to its ancient esteem in the minds of the liberal, and shew how much it is perverted by applying it to contrary purposes.
In order to this, I shall endeavour to prove the following position, that things valuable for their own sakes, are preferable to such as refer to something else. Now, this may be demonstrated, by considering that every natural production was made with reference to some end, as is evident from an induction of particulars; and if this be the case, it may be safely inferred, that every thing exists for the sake of the end. But that for the sake of which any being subsists is the best of all; and the end, according to nature, is that which is perfected the last of all, from the birth of any being. Hence the human body receives its end or perfection first, but the soul last. And hence the soul is posterior to the body, in the accomplishment of its nature; and its ultimate perfection is wisdom. It is on this account that old age alone pursues and desires the goods of prudence and wisdom. Hence, wisdom is a certain end to us according to nature; and to be wise, is the extreme[ciii] or final cause for which we were produced. It was, therefore, beautifully said by Pythagoras, that man was constituted by divinity, that he might know, and contemplate. If then wisdom be the end of our nature, to be endued with wisdom must be the best of all. So that other things are to be performed for the sake of the good which this contains. But to enquire in every science something besides this, and to require that it should be useful, is alone the employment of one ignorant of the great difference between the most illustrious goods, and things necessary. For they differ, indeed, widely; since things are to be called necessaries, which are the objects of desire for the sake of others, and without which it is impossible to live. But those concerns alone are properly good, which are loved by themselves, though nothing else should fall to the lot of their possessor; for one thing is not to be desired for the sake of another infinitely, but it is requisite to stop at some limited object of desire, of which it would be ridiculous to require any utility abstracted from itself. But you will ask, What is the emolument of contemplative wisdom, what the good it confers on its possessor? What if we should say (for such is the truth of the case) that it transports us by intellect and cogitation, to regions similar to the fortunate islands; for utility and necessity are strangers to those happy and liberal realms. And if this be admitted, ought we not to blush, that having it in our power to become inhabitants of the fortunate islands, we neglect the pursuit, through a sordid enquiry after what is useful and profitable according to vulgar estimation? The rewards of science, therefore, are not to be reprehended, nor is it a trifling good which results from its acquisition. Besides, as men travel to the mountain Olympus for its spectacle alone, preferring a view of its lofty summit to much wealth; and[civ] as many other spectacles are desired for their own sakes, and valued beyond gold, in like manner the speculation of the universe is to be prized above every thing which appears useful to the purposes of life: for it is surely shameful that we should eagerly frequent the theatre, and the race, for the sake of the delight afforded to our corporeal sight, and should look for no farther utility in these than the pleasure they produce; and yet should be so sordidly stupid as to think that the nature of things, and truth itself are not to be speculated without some farther reward than the sincere delight their contemplation affords.
It is on this account that the apprehension of truth is compared to corporeal vision; for the sight is the most liberal of all the senses, as is confirmed by the general testimony of mankind. Hence, the sight of the sun and moon, and the glorious spectacle of the stars is desired by the most illiterate as well as the most knowing, for the delight such visions afford; while, on the contrary, the desires of the other senses are for the most part directed to something farther than the mere objects of their energy. Thus, even the sense of hearing, which is the next in dignity to the sight, is not always desirable for its own sake; for light is the general object of sight, and sound that of hearing; but it is evident that light is more universally desired than sound, since all light, when not excessive, is always pleasing, but this is by no means the case with every kind of sound. Hence it is, that all contemplation is so delightful, and this in proportion as it becomes abstracted from sensible objects; for the most beautiful forms do not produce genuine delight, until they are strongly represented in the phantasy, as is evident in the passion of love; since the fairest face then alone causes love when it presents itself clearly to the inward eye of thought, in the mirror of[cv] imagination, accompanied with living elegance, and a resistless energy of form.
Indeed, so liberal and so exalted an employment is contemplation, that Plotinus, with his usual profundity, proves that the universe subsists for its sake; that all the productions of nature originate from this; and that even actions themselves are undertaken with a view to the enjoyment of after-speculation. May we not, therefore, say that the sportsman follows the chace for the sake of a subsequent review of his favourite pursuit? That the glutton for this rejoices in the meal; and even the miser in his wealth? And that conversation is alone sollicited, that it may recal past images to the soul? In short, contemplation is the first spring of action, and its only end; since we are first incited to any external object by speculating its image in the phantasy: and our subsequent conduct tends, without ceasing, to the energy of reflection; for destroy prior and posterior contemplation, and action is no more.
Now if this be the case, and if geometry is a speculative science (I mean the geometry of the ancients), it is both desirable for its own sake, and for still higher contemplations, the visions of intellect, to which it is ultimately subservient. For, when studied with this view, it opens the eye of the soul to spectacles of perfect reality, and purifies it from the darkness of material oblivion. Away then, ye sordid vulgar, who are perpetually demanding the utility of abstract speculations, and who are impatient to bring down and debase the noblest energies, to the most groveling purposes; ignorant of that mighty principle of action, which influences every part of the universe, and through which even division and discord tend as much as possible to union and consent; ignorant that from the depravity of your nature, and the blindness of your inward eye, you[cvi] are incapable of speculating the substance of reality, and are therefore eagerly gazing on its shadow: and lastly, unconscious that this is the point about which you are continually making excentric revolutions, mistaking the circumference for the centre, motion for rest, and a departure from good for a tendency to felicity.
It was for the sake of this most exalted and liberal contemplation that Heraclitus yielded his right of succession to a throne, to his brother; and that Anaxagoras neglected his patrimony, esteeming one drop of genuine wisdom preferable to whole tuns of riches. Led by a desire of this, as by some guiding star, Pythagoras travelled into Egypt, and cheerfully encountered the greatest difficulties, and maintained the most obstinate perseverance, until at length he happily penetrated the depths of Egyptian wisdom, and brought into Greece a treasury of truth for future speculation. But these were happy days; this was the period destined to the reign of true philosophy, and to the advancement of the human soul to the greatest perfection its union with this terrene body can admit. For in our times, the voice of wisdom is no longer heard in the silence of sacred solitude; but folly usurping her place, has filled every quarter with the barbarous and deafning clamours of despicable sectaries; while the brutal hand of commerce has blinded the liberal eye of divine contemplation. For unfortunately, the circle of time, as it produces continual variations, at length reverses the objects of pursuit; and hence, that which was once deservedly first, becomes at length, by a degraded revolution, the last in the general esteem.
2. If geometry, therefore, be both valuable for its own sake, and for its subserviency to the most exalted contemplations, there can be no doubt but that the great perfection[cvii] to which this science was brought by the Greeks, was entirely owing to their deep conviction of this important truth. Euclid, we are informed by Proclus, in this work, was of the Platonic sect; and Archimedes is reported, by Plutarch, in his Life of Marcellus, to have possessed such elevated sentiments of the intrinsic dignity of geometry, that he considered it perverted and degraded, when subservient to mechanical operations; though, at the request of king Hiero, he fabricated such admirable engines for the defence of Syracuse. From this source alone, the great accuracy and elegance of their demonstrations was derived, which have been so deservedly applauded by the greatest modern mathematicians, and the warmest advocates for the farrago of algebraic calculation. Algebra, indeed, or as it is called, specious analysis, is the modern substitute for the perfect method adopted by the ancients in geometrical demonstrations; and this solely, because it is capable of being applied with greater facility to the common purposes of life. Hence, hypotheses have been eagerly admitted in geometry, which the ancients would have blushed to own: I mean the multiplications and divisions of lines and spaces as if they were numbers, and considering geometry and arithmetic as sciences perfectly the same. But we have fortunately the testimony of the first mathematicians among the moderns against the unlawfulness of this ungeometrical invasion. And to begin with the great sir Isaac Newton, in his Universal Arithmetic[29]: “Equations (says he) are expressions of arithmetical computation, and properly have no place in geometry, except so far as quantities truly geometrical (that is, lines, surfaces, solids, and proportions), may be said to be some equal to others. Multiplications, divisions, and such sort of computations, are newly received[cviii] into geometry, and that unwarily, and contrary to the first design of this science. For whoever considers the construction of problems by a right-line and a circle, found out by the first geometricians, will easily perceive that geometry was invented that we might expeditiously avoid, by drawing lines, the tediousness of computation. Therefore, these two sciences ought not to be confounded. The ancients so industriously distinguished them from one another, that they never introduced arithmetical terms into geometry. And the moderns, by confounding both, have lost the simplicity in which all the elegancy of geometry consists.” And in another part[30] of the same work he observes, that “the modern geometers are too fond of the speculation of equations.” To this very high authority we may add that of Dr. Halley, in the preface to his translation of Apollonius de Sectione Rationis; for which work he conceived so great an esteem, that he was at the pains to learn Arabic in order to accomplish its translation into Latin[31]: “This method, says he, (of Apollonius) contends with specious algebra in facility, but far excels it in evidence and elegance of demonstrations; as will be abundantly manifest if any one compares this doctrine of Apollonius de Sectione Rationis, with the algebraic analysis of the same problem, which the most illustrious Wallis exhibits in the second volume of his mathematical works, cap. liv. p. 220.” And in the conclusion of his preface, he observes[32], “that it is one thing to give the resolution of a problem some how or other, which may be[cix] accomplished by various ways, but another to effect this by the most elegant method; by an analysis the shortest, and at the same time perspicuous; by a synthesis elegant, and by no means operose.” And Dr. Barrow, notwithstanding he was so great an advocate for the identity of arithmetic and geometry, expressly asserts[33], that algebra is no science. To these authorities we may add Simson and Lawson, who, sensible of the superior skill of the ancients, both in analysis and synthesis, have made laudable attempts to restore the Greek geometry to its pristine purity and perfection.
Again, the greatest men of the present times have been of opinion, that algebra was not unknown to the ancients; and if this be true, their silence respecting it is a sufficient proof of their disapprobation. Indeed, if we consider it when applied to geometry, as an art alone subservient to the facility of practice, as conveying no evidence, and possessing no elegance of demonstration, we shall not wonder at its being unnoticed by the ancients, with whom practice was ever considered as subservient to speculation; and in whose writings elegance of theory and accuracy of reasoning are found perpetually united.
3. But the lives of the first cultivators of this science (I mean the Egyptian priests) as well as of the Pythagoreans and Platonists, by whom it afterwards received such improvements, sufficiently evince that this science advanced to perfection from an intellectual theory as its source, and from being referred to contemplation as its end; and this will be evident, by attending to the following history of the Egyptian priests, as preserved to us by Porphyry, in his excellent work on abstinence[34]; a translation of which will not, I presume, be unacceptable to the philosophical[cx] reader, “Chæremon, the Stoic (says he) explaining the rites of the Egyptian priests, who, he says, are accounted philosophers by the Egyptians, relates, that they choose a place best adapted to the study and performance of sacred rites; so that a desire of contemplation is excited by only frequenting those recesses which are dedicated to their use, and which procure safety to the priests, on account of that reverence of the divinity, whose sacred mysteries they perform; so that all possible honour is paid to these philosophers, in the same manner as to some sacred animals. But he says they live entirely solitary, except at particular times, when they mix with others in such assemblies as are usually held, and in public feasts; and that on all other occasions they are scarcely to be approached. For he who desires to converse with them must first purify himself, and abstain from a multitude of things after the manner of these Egyptian priests. He adds, that these men, renouncing every other occupation, and all human affairs, give themselves entirety, through the whole of life, to the contemplation of divine concerns, and to enquiring into the divine will: by the latter of these employments procuring to themselves honour, security, and the estimation of piety; by contemplation, tracing out the latent paths of science; and by both these occupations united, accustoming themselves to manners truly occult, and worthy of antiquity. For to dwell always on divine knowledge, and be disposed for divine inspiration, removes a man beyond all immoderate desires, calms the passions of the soul, and raises her intellectual eye to the perception of that which is real and true. But they studied tenuity of aliment, and frugality in their apparel, and cultivated temperance and patience, together with justice and equity, in all their concerns. Indeed, a solitary life rendered them perfectly venerable; for during that period[cxi] which they call the time of purification, they scarcely mixed with the associates of their own order, or saw any one of them, except him who was conversant with them in that exercise of purity, on account of necessary uses. But they by no means concerned themselves with those who were unemployed in the business of purification. The remaining part of their time they conversed familiarly with those similar to themselves; but they lived separate and apart from those who were estranged from their ceremonies and manner of living. He adds, they are always seen employed among the resemblances of the gods, either carrying their images, or preceding them in their accustomed processions, and disposing them with gravity of deportment, and in a graceful order. In all which operations they did not indicate any pride of disposition; but exhibited some particular natural reason. But their gravity was conspicuous from their habit; for when they walked, their pace was equable, and their aspect so perfectly steady, that they refrained from winking whenever they pleased. Their risibility too, extended no farther than to a smile. But their hands were always contained within their garments; and as there were many orders of priests, every one carried about him some remarkable symbol of the order he was allotted in sacred concerns. Their sustenance too was slender and simple; and with respect to wine, some of them entirely refrained from it; and others drank it very sparingly, affirming that it hurt the nerves, was an impediment to the invention of things, and an incentive to venereal desires. They also abstained from many other things, never using bread in exercises of purity; and if they ate it at other times, it was first cut in pieces, and mingled with hyssop. But they abstained, for the most part, from oil, and when they used it mixt with olives, it was only in[cxii] small quantities, and as much as was sufficient to mitigate the taste of the herbs.
In the mean time, it was not lawful for any one to taste of the aliment, whether solid or fluid, which was brought into Egypt from foreign parts. They likewise abstained from the fish which Egypt produced; and from all quadrupeds having solid or many fissured hoofs; from such as were without horns; and from all carniverous birds: but many of them abstained entirely from animal food. And at those times when they all rendered themselves pure, they did not even eat an egg. But when the time drew near in which they were to celebrate some sacred rites, or festival, they employed many days in previous preparation, some of them setting apart forty-two days, others a greater length of time than this; and others again a shorter; but never less than seven days; abstaining, during this period, from all animals, and from all leguminous and oily nutriment, but especially from venereal congress. Every day, they washed themselves three times in cold water; after rising from bed, before dinner, and when they betook themselves to rest. And if they happened to be polluted in their sleep, they immediately purified their bodies in a bath. They made cold water too subservient to the purposes of purification at other times, but not so often as the bath. Their beds were composed from the branches of palm, which they called βαίς, bais. A piece of wood, of a semi-cylindrical form, and well planed, served them for a pillow. But through the whole of life, they were exercised in the endurance of hunger and thirst, and accustomed to a paucity and simplicity of nutriment.
But as a testimony of their temperance, though they neither used the exercise of walking nor riding, yet they lived free from disease, and were moderately strong. For,[cxiii] indeed, they endured great labour in their sacred ceremonies, and performed many services exceeding the common strength of men. They divided the night between observations of the celestial bodies, and offices of purity; but the day was destined by them to the cultivation of the divinities, whom they worshiped with hymns each day three or four times; in the morning and evening, when the sun is at his meridian, and when he is setting. But the rest of their time they were occupied in arithmetical and geometrical speculations, always laborious and inventing, and continually employed in the investigation of things. In winter nights also, they were diligent in the same employments, and were ever vigilant to literary studies; since they were not solicitous about external concerns, and were freed from the base dominion of intemperate desires. Their unwearied and assiduous labour, therefore, is an argument of their great patience; and their continence is sufficiently indicated by their privation of desire. Besides this, it was esteemed very impious to sail from Egypt, as they were particularly careful in abstaining from the manners and luxuries of foreign nations; so that to leave Egypt was alone lawful to those who were compelled to it by state necessities. But they discoursed much concerning a retention of their native manners; and if any priest was judged to have transgressed the laws in the least particular, he was expelled from the college. Besides, the true method of philosophizing was preserved in Commentaries and Diaries, by the prophets and ministers of sacred concerns: but the remaining multitude of priests, Pastophori, or priests of Isis and Osiris, governors of temples, and servants of the gods, studied purity, yet not so exactly, nor with so great continence as those we have mentioned. And thus much is related of the Egyptians, by a man who is equally a lover of truth, and of accurate[cxiv] diligence, and who is deeply skilled in the Stoic philosophy.”
4. But the lives of the Pythagoreans and Platonists, who carried this divine science to its ultimate perfection, no less eminently evince the truth of our position. For, as Porphyry informs us, in the same invaluable treatise[35], “some of the ancient Pythagoreans, and wise men, inhabited the most desert places; and others retired into temples, from which the multitude and every tumult were expelled. But Plato was willing to fix his academy in a place not only solitary, and remote from the city, but, as they report, insalubrious. Others, again, have not spared their eyes, through a desire of more perfectly enjoying that blissful contemplation, from which they wished never to be separated.” After this, he presents us with a description from Plato[36] of those intellectual men, by whom the world has been enlightened with the sublimest wisdom and truth: “For it was not falsly, or in vain (says he), that a certain philosopher, speaking of contemplative men, affirms, that such as these are ignorant, from their early youth, of the way which leads to the forum, or in what place the court or senate-house is situated, or any public council of the state. They neither see nor hear the laws, whether decreed or promulgated, or written; and with respect to the factions and contentions of their companions for magistracy, for assemblies and splendid entertainments, luxurious eating and minstrels, they do not even think of these as in a dream. Such an one knows no more of the evil which has happened to some one of his ancestors, whether male or female, or any thing belonging to them, than how many pitchers of water are contained in the sea. Nor does he abstain from things of this nature for the sake of acquiring[cxv] fame; but in reality, his body alone abides in the city, and wanders about from place to place, but his intellect esteeming all these as of small importance, or rather as non-entities, he despises them, and, according to Pindar, “from these on every side he soars:” by no means applying himself to things which are near him, and to sensible concerns.”
If such then were the lives of the men who brought this contemplative science to its present perfection, and who are to this day our masters in geometry; if such were the exalted sentiments they entertained of its dignity and worth, what greater proof can we require of its being valuable for its own sake, and as subservient to the energies of intellect? We have ample evidence too, of its being degraded when brought down to the common purposes of life, in the example of those who, with this view, have disguised it with the dark and sordid involutions of algebraic calculation; for it was solely to facilitate practice, that this barbarous invasion has been admitted by the moderns. Let me then be permitted to persuade the few who study geometry in its ancient purity, and who consider the ruins of Grecian literature on this, as well as on every other science, the models of perfection, to enter with avidity on the study of the ensuing Commentaries, and endeavour to fathom the depth of our profound and elegant philosopher: for by this means they may happily obtain the end of all true science, the purification of the soul; and be able to draw the light of perfect wisdom, from the undecaying and inexhaustible fountain of good.
But if it should be asked in what these energies of intellect consist, to which all science ultimately refers? I answer, in the contemplation of true being, or those ideal and divine forms, with which the intelligible world is replete.[cxvi] Now this great end is not to be accomplished without previous discipline, a long exercise of the reasoning power, and a continued series of philosophic endurance. For this end, when attained, is no other than the enjoyment of that felicity congenial to the soul previous to her immersion in body. But, for the further information of the liberal reader on this important subject, the following paraphrases from Porphyry and Proclus are subjoined; the former instructing us in the various purifications necessary to this end; and the latter exhibiting the gradations by which we may rise to the speculation of reality, and (leaving all multitude behind) ascend to the divinely solitary principle of things, the ineffable One.
5. “In the first place, then (says Porphyry[37]) my reasons are not addressed to those who are occupied in illiberal arts, nor to those engaged in corporeal exercises, neither to soldiers nor sailors, neither to rhetoricians nor to those who have undertaken the duties of an active life. But I write to the man continually employed in thinking what he is, from whence he comes, and whither he ought to tend: and who, with respect to every thing pertaining to food, and other offices of life, is entirely changed from those who propose to themselves a different manner of living; for to a man of this kind alone is my present discourse addressed. Indeed, in this common state of existence, one and the same mode of persuasion cannot be addressed to the sleeper, who, if it was possible, would conciliate to himself perpetual sleep, and who, for this purpose, seeks on every side for soporiferous incentives, as to him who studies continually to drive away sleep, and to dispose every thing about him to vigilance and intellectual activity. But to the former, it is necessary to advise intoxication, surfeiting,[cxvii] and satiety, and to recommend a dark house; and, as the poets say, a bed luxurious, broad, and soft. Such a one should chuse whatever tends to produce stupor, and give birth to indolence and oblivion, whether consisting of odours, ointments, or medicaments which are accustomed to be eat or drank. But it is necessary that the intellectual man should use sober drink, unmixed with the lethargic fumes of wine; nutriment slender, and almost approaching to fasting; a lucid house, receiving a subtle air and wind; that he should be continually agitated with cares and griefs; and lastly, that he prepares for himself a small and hard bed, while thus employed in purifying his soul from the stains contracted by corporeal involution. But whether we are born for this exalted purpose, I mean for vigilant intellectual energies, allowing as small a part of our life as possible to sleep; (since we do not exist in a place where souls perpetually vigilant abide), or whether we are destined to a contrary purpose, I mean, to sleep and oblivion, would be foreign from our design to explain; and would require a longer demonstration than the limits of our work will admit.
But whoever once cautiously surmizes the delusions of our life in the present world, and the inchantments of this material house in which we are employed, and who perceives himself naturally adapted to vigilant energies; lastly, who apprehends the soporiferous nature of the place in which he acts, to such a one we would prescribe a diet congruous to his suspicion of this fallacious abode, and to the knowledge he possesses of himself; in the mean time, advising him to bid a long farewel to the sleeper, stretched on his couch, as on the lap of oblivion. Nevertheless, we should be careful lest, as those who behold the bleer-eyed, contract a similar defect, and as we gape when present with those who are gaping, so we should be filled with[cxviii] drowsiness and sleep, when the place in which we reside is cold, and adapted to fill the eyes with watery humours, from its abounding with marshes and vapours, which incline their inhabitants to heaviness and sleep. If then, legislators had composed the laws with a view to the utility of the state, and had referred these to a contemplative and intellectual life as their end, we ought to submit to their institutions, and acquiesce in the diet they have prescribed for our subsistence. But if they, only regarding that life which is according to nature, and is called of the middle kind, ordain such things as the vulgar admit, who only estimate good and evil as they respect the body, why should any one, adducing these laws, weary himself in endeavouring to subvert a life which is far more excellent than every law written and composed for the sake of the vulgar, and which follows a law not written, but divinely delivered? For such is the truth of the case.
That contemplation which procures us felicity, is not a mass of discourses, and a multitude of disciplines; or, as some may think, consisting from hence; nor does it receive any increase from a quantity of words. For if this was the case, nothing could hinder those from being happy, who comprehend all disciplines, and are accurately skilled in a variety of languages. But the whole circle of the sciences cannot by any means accomplish this blissful contemplation, nor even those disciplines which are conversant with true and substantial being, unless there is also a conformation of our nature and life to this divine end. For since there are, as they say, three ends of living, if we regard the particular objects to which mankind tend, the end with us is to follow the contemplation of true being, promoting, as much as possible, by an acquisition of this kind, an intimate union of the contemplating individual[cxix] with the object of contemplation. For, in nothing else besides true being, is it possible for the soul to return to its pristine felicity; nor can this be effected by any other conjunction. But intellect is true being itself: so that the proper end is to live according to intellect. And on this account, exoteric discourses and disciplines, retarding the purgation of the soul, are far from filling up the measure of our felicity. If then, felicity was defined by the comprehension of words or sciences, they who do not pay a proper attention to the kind and quantity of their food, nor to any thing else pertaining to their present existence, might obtain this end: but since it is requisite to change our life, and to be pure both in speech and action, let us consider what discourses and what works may render us partakers of this most necessary means of acquiring substantial felicity.
Are, then, those things which separate us from sensible objects, and from the affections which they excite, and which lead to a life intellectual, and void of imagination and passion, are these the means we are in pursuit of? So that every thing contrary is foreign from our purpose, and worthy to be rejected? And in such proportion as it draws us aside from intellect? Indeed, I think it is consonant to truth, that we should eagerly contend where intellect leads; for in this material abode, we are similar to those who enter or depart from a foreign region, not only in casting aside our native manners and customs, but from the long use of a strange country, we are imbued with affections, manners, and laws foreign from our natural and true region, and with a strong propensity to these unnatural habits. Such an one, therefore, should not only think earnestly of the way, however long and laborious, by which he may return to his own, but that he may meet with a[cxx] more favourable reception from his proper kindred, should also meditate by what means he may divest himself of every thing alien from his true country, which he has contracted; and in what manner he may best recal to his memory, those habits and dispositions without which he cannot be admitted by his own, and which, from long disuse, have departed from his soul. In like manner, it is requisite, if we wish to return to such things as are truly our own, and proper to man considered as a rational soul, to lay aside whatever we have associated to ourselves from a mortal nature, together with all that propensity to material connections, by which the soul is allured, and descends into the obscure regions of sense; but to be mindful of that blessed and eternal essence intellect, our true father, and hastening our return to the contemplation of the uncoloured light of good, to take especial care of these two things; one, that we divest ourselves (as of foreign garments) of every thing mortal and material; the other how we may return with safety, since thus, ascending to our native land, we are different from ourselves before we descended into mortality. For we were formerly intellectual natures; and even now we are essences purified from every stain contracted by sense, and from that part which is destitute of reason: but we are complicated with sensible connections, on account of our impotence and infirmity, which is the cause that we cannot always be conversant with intellectual concerns; but with mundane affairs we can be present with frequency and ease; for all our energetic powers are stupified and clouded with oblivion, through body and sense; the soul not remaining in an intellectual state; (as the earth when badly affected, though good fruit is deposited in its bosom, produces nothing but weeds); and this, through the improbity of the soul, which does not,[cxxi] indeed, destroy its essence, while it acquires brutality; but by such an accession it becomes complicated with a perishing nature, is bound in the dark folds of matter, and is drawn aside from its proper state, into one that is foreign and base.
So that it is highly requisite to study, if we are solicitous of returning to our pristine state of felicity, how to depart from sense and imagination, and her attendant brutality, and from those passions which are raised by her phantastic eye, as much as the necessity of our nature will permit. For the intellect must be accurately composed; and it is proper it should obtain a peace and tranquility free from the contentions of that part which is destitute of reason, that we may not only hear with attention concerning intellect and intelligible objects, but to the utmost of our ability, may enjoy their contemplation; and thus, being reduced into an incorporeal nature, may truly lead an intellectual life, and not in a false delusive manner, like these who are at the same time entangled with corporeal concerns. We must, therefore, divest ourselves of the various garments of mortality by which our vigour is impeded; as well this visible and fleshly garment, as that more interior one with which we are invested contiguous to the skin. We must enter the place of contest naked, and without the incumbrance of dress, striving for the most glorious of all prizes, the Olympiad of the soul. But the first requisite, and without which it is not lawful to contend, is, that we strip off our garments. And since our vestments are some of them exterior, and some interior, so with respect to the denudation of the soul, one process is by things more open, another by such as are more occult. For instance, not to eat, or not to accept what is offered, is among things obvious and open; but not to desire is more obscure; so that[cxxii] it is here requisite not only to abstain from things improper in deeds, but likewise in desire. For what does it profit to abstain in actions from what is base, in the mean time adhering to the causes which produce such actions, as if bound in indissoluble chains?
But this receding from material affections is brought about partly by force, and partly by persuasion; and by the assistance of reason the affections languish, and are, as it were, buried in oblivion, or in a certain philosophical death; which is, indeed, the best mode of desertion, without oppressing the terrene bandage from which the soul departs. For in things which are the objects of sense, a violent devulsion cannot take place without either a laceration of some part, or at least a vestige of separation. But vice steals in upon the soul through continual negligence: and carelessness is produced by not sufficiently attending to intelligible objects; the affections in the mean time being excited by the drowsy perceptions of sense, among which must be also reckoned the sensations arising from food. We must therefore abstain, not less than from other things, from such food as usually excites the passions of our soul. Let us then in this particular enquire a little farther.
There are two fountains, whose noxious streams detain the soul in matter, and with which, as if saturated with lethargic potions, she forgets her own proper speculations: I mean pleasure and grief, the artificer of which is sense and its perceptions, together with the operations attendant on the senses, imaginations, opinions, and memory. The passions, roused by the energies of these, and the irrational part, now fattened with noxious nutriment, draw down the soul, and avert her inclinations from her native love of true being. It is requisite, therefore, that we revolt[cxxiii] from these to the utmost of our ability. But true defections can alone take place by avoiding the passions and rash motions produced by the senses. But, sensation respects whatever moves the sight, or the hearing, or the taste, or the smell. And sense is, as it were, the metropolis of that foreign colony of passions which reside in the soul, and which must be expelled by him who wishes, while connected with body, to become an inhabitant of the royal regions of intellect. Let us then enquire how much fuel of the passions enters into us through each of the senses; and this either when we behold the spectacles of horses in the race, and the labours of the athletic, or the contests of those who twist and bend their bodies in leaping, or when we survey beautiful women. For all these insnare us, unconscious of the danger, and subject to their dominion the irrational appetite, by proffered inchantments of every kind.
For by all such inchantments the soul, as if driven into fury, compels the compound man to leap rashly, and without reason, and full of the brutal nature to bellow and exclaim. In the mean time, the perturbation appearing from without, being inflamed by the internal, which was first of all roused by sense. But the vehement motions excited by the hearing, arise from certain noises and sounds, from base discourse, and mixed assemblies; so that some, exiled from reason, behave as if struck mad; and others, enervated by effeminate softness, agitate themselves by a multitude of trifling gesticulations. And who is ignorant how much the soul is fattened, and infested with material grossness, by the ointments and perfumes which commend lovers to each other? But why is it necessary to speak of the passions originating from the taste: in this respect especially, binding the soul in a double band; one of which is[cxxiv] thickened by the passions excited by the taste; the other becomes strong and powerful by the different bodies which we receive in food. For as a certain physician observed, those are not the only poisons which are prepared by the medical art, but such things as we daily receive for food, as well liquid as solid, are to be reckoned among this number; and much greater danger arises to our life from these, than to our bodies from poisons. But the touch does all but transmute the soul into body, and excites in it, as in a dissonant body, certain broken and enervated sounds. The remembrance, imagination, and cogitation of all these raise a collected swarm of passions, i. e. of fear, desire, anger, love, emulation, cares, and griefs, they fill the soul with perturbations of this kind, cloud its intellectual eye with oblivion, and bury its divine light in material darkness.
On which account it is a great undertaking to be purified from all this rout of pollutions; and to bestow much labour in meditating day and night, what measures we shall adopt to be freed from these bonds, and this because we are complicated with sense, from a certain necessity. From whence, as much as our ability will permit, we ought to recede from those places in which we may (perhaps unwillingly), meet with this hostile rout; and it is requisite we should be solicitous not to engage in combat with these dangerous foes, lest, through too great a confidence of victory and success, instead of vigorous contention, we produce only unskilfulness and indolence.”
And in the conclusion of the first book, he adds, “For, indeed, if it be lawful to speak freely, and without fear, we can by no other means obtain the true end of a contemplative, intellectual life, but by adhering to the Deity (if I may be allowed the expression), as if fastened by a nail, at the same time being torn away and separated from[cxxv] body and corporeal delights; having procured safety from our deeds, and not from the mere attention to words. But if friendship is not to be conciliated with a divinity, who is only the governor of some particular region, with any kind of food, or by the use of animal nutriment, much less can a gross diet effect an union with that God who is exalted above all things, and who is superior to a nature simply incorporeal; but after every mode of purgation, and the greatest chastity of body, and purity of soul, we shall scarcely be thought worthy to obtain the vision of his ineffable beauty; though this is sometimes permitted to him whose soul is well disposed, and who has passed through life with the greatest sanctity and purity of manners. So that, by how much the Father of all exceeds every nature in simplicity, purity, and self-sufficiency, as being infinitely remote from all suspicion of material contagion, by so much the more ought he who approaches to the Deity, to be entirely pure and holy, first in his body, and afterwards in the most secret recesses of his soul; having distributed a purgation adapted to every part, and being completely invested with purity, as with a transparent garment, fit for the intimate reception of divine illumination.” Thus far Porphyry, whose excellent sentiments on this subject are a lasting monument of the elevation and purity of soul which the Platonic philosophy affords; and at the same time sufficiently prove the arrogance and ignorance of those who depreciate the wisdom of the ancients, and consider their greatest philosophers as involved in mental darkness and delusion. But presumption of this kind is continually increased by indolence, and strengthened by interest; and it is common to find scribblers of every kind, laughing at Plato and his philosophy, who are too mean for criticism, and even too insignificant for contempt. Let us, therefore, leave such[cxxvi] in their native inanity, and listen to the instructions of the divinely elegant Proclus, by which we may ascend to the contemplation of true being, and the ineffable principle of things.
6. [38]“Pythagoras and Plato command us to fly from the multitude, that we may pursue the most simple truth, and apply ourselves wholly to the contemplation of real being. From the multitude of exterior people drawing us aside in various ways, and deceiving us by fallacious appearances. But much more to shun the multitude of interior people; for this much more distracts and deceives. We must, therefore, fly from the various multitude of affections, the obscure informations of sense, the shadowy objects of imagination, and the dusky light of opinion. For every multitude of this kind is so different in itself, that its parts are contrary to one another; from whence it is necessary to betake ourselves to the sciences, in which multitude has no contrariety. For though affections are contrary to affections, one perception of sense to another, imaginations to imaginations, and opinions to opinions, yet no one science is found contrary to another. In this multitude, therefore, of propositions and notions, we may collect into one the number of sciences binding them in one according bond. For they are so remote from contrariety to each other, that notion is subservient to notion, and inferior sciences minister to superior, depending on them for their origin. Above all, it is here necessary, from many sciences which pre-suppose one, to betake ourselves to one science itself, no longer supposing another, and in an orderly series to refer them all to this original one. But after science, and its study, it will be necessary to lay aside compositions, divisions,[cxxvii] and multiform discourses, and from thence to ascend to intellectual life, to its simple vision, and intimate perception. For science is not the summit of knowledge, but beyond it is intellect; not that intellect only which is separated from soul, but the illustration infused from thence into the soul, which Aristotle affirms to be the intellect by which we acknowledge the principles of science; and Timæus says, that this exists in no place but the soul. Ascending, therefore, to this intellect, we must contemplate together with it intelligible essence, by indivisible and simple perceptions, speculating the simple genera of beings. But after venerable intellect itself, it will be proper to contemplate that summit of the soul, by which we are one, and under whose influence our multitude is united. For as by our intellect we touch the divine intellect; so by our unity, and as it were the flower of our essence, it will be lawful to touch that first one, from whom all subordinate unities proceed. And by this our one, we are especially conjoined with divinity. For similitude may be every where comprehended by that which is similar; the objects of knowledge by science; things intelligible by intellect; and the most unifying measures of being, by the unity of the soul. But this unity and its energy is the summit of our actions; for by this we become divine, when, flying from all multitude, we retire into the depths of our unity, and, being collected into one, uniformly energize. Thus far we admonish to shun the multitude, by steps proceeding from the order of knowledge: in the next place, we shall proceed in the same design by the series of knowable objects. Fly then every sensible species, for they are heaped together, are divisible, and perfectly mutable, and incapable of affording sincere and genuine knowledge. From these dark informations, therefore, betake yourself[cxxviii] to incorporeal essence; since every sensible object possesses adventitious unity, is by itself scattered and confused, and full of formless infinity. Hence its good is divisible, and adventitious, distant and separated from itself, and residing in a foreign seat. When you have ascended thither, and are placed among incorporeal beings, you will behold above the fluctuating empire of bodies, the sublime animal order, self-moving, spontaneously energizing in itself, and from itself possessing its own essence, yet multiplied, and anticipating in itself a certain apparition or image of the essence divisible about the unstable order of bodies. You will there perceive many habitudes of reasons, various proportions, and according bonds. Likewise the whole and parts, vivid circles, and a multiform variety of powers; together with a perfection of souls not-eternal, not subsisting, together as a whole, but, unfolded by time, gradually departing from their integrity, and conversant with continual circulations. For such is the nature of the soul.
But after the multitude belonging to souls, betake yourself to intellect, and the intellectual kingdoms, that you may possess the unity of things. There remain in contemplation of a nature ever abiding in eternity, of life ever flourishing, intelligence ever vigilant, to which no perfection of being is wanting, and which does not desire the chariot of time, for the full energy of its essence. When you have beheld natures of this exalted kind, and have seen by how great an interval they are superior to souls; in the next place enquire whether any multitude is there, and if intellect, since it is one, is also universal; and again, since it is uniform, if not also multiform: for you will find it subsists after this manner. When, therefore, you have intimately beheld this intellectual multitude, though profoundly indivisible and united, transport yourself again[cxxix] to another principle, and having considered, as in a more exalted rank, the unities of intellectual essences, in the last place proceed to unity perfectly separate and free from all things. And when advanced thus far, lay aside all multitude, and you will at length arrive at the ineffable fountain of good. And since it appears, from these various gradations, that the soul then properly obtains perfection, when she flies from all external and internal multitude, and the boundless variety of the universe, we may likewise conclude from hence, that our souls do not alone collect their knowledge from the obscure objects of sense, nor from things particular and divisible discover a perfect whole, and a perfect one, but draw forth science from their inmost recesses, and produce accuracy and perfection from whatever in appearances is inaccurate and imperfect. For it is not proper to suppose that things false and obscure, should be the principal sources of knowledge to the soul; and that things discordant among themselves, which require the reasonings and arguments of the soul, and which are ambiguous and confused, should precede science which is immutable; nor that things variously changed, should generate reasons abiding in one; nor that indeterminate beings should exist as the causes of determinate intelligence. It is not, therefore, fit to receive the truth of eternal entities from boundless multitude; nor from sensible objects the judgment of universals; nor from things destitute of reason, accurate discrimination of that which is good: but it is proper that the soul, retiring into her immortal essence, should there scrutinize the good and the true, and the immutable reasons of all things: for the essence of the soul is full of these, though they are clouded by oblivion. The soul, therefore, beholding exteriors, enquires after truth, in the mean time possessing it in the depths of her essence,[cxxx] and deserting herself, explores the good in the dark regions of matter. Hence, every one in the pursuit of reality ought to begin with the knowledge of himself. For, if we constantly extend our views among the multitude of men, we shall never discern the one species man, obscured by the multitude, and distracted by the division and discord, and the various mutations of those who participate the species. But if we turn our eye inwards, there, remote from perturbation, we shall behold one reason and nature of men; since multitude is an impediment to the conversion of the soul into herself. For here variety darkens unity, difference obscures identity, and dissimilitude clouds similitude; since species are confused in the folds of matter; and every where that which is excellent is mixed with the base.” Thus far Proclus; and thus much for our intended Dissertation.
LIFE
AND
COMMENTARIES
OF
PROCLUS.
[1]
THE
LIFE OF PROCLUS,
BY MARINUS[39];
OR,
CONCERNING FELICITY.
When I consider the magnitude of mind, and dignity of character belonging to Proclus, a philosopher of our time, and attend to those requisites, and that power of composition which those ought to possess who undertake a description of his life; and[2] lastly, when I regard my own poverty of diction, I am inclined to believe it more proper to refrain from such an undertaking, not to leap over the fosse (according to the proverb), and to decline a discourse involved in so much difficulty and danger. But my scruples are something diminished when I consider, on the other hand, that even in temples, those who approach to the altars do not all sacrifice alike; but that some are solicitously employed in preparing bulls, goats, and other things of a similar kind, as not unworthy the beneficence of the Gods to whom those altars belong: likewise that they compose hymns, some of which are more elegant in verse, but others in prose; while some, who are destitute of all such gifts, and sacrifice with nothing more perhaps than a cake and a small quantity of bread, with frankincense, and who finish their invocations with a short address to the particular divinity they adore, are not less heard than others. While I thus think with myself, I am afraid, according to Ibycus[40], lest I should not offend against the Gods (for these are his words) but against a wise man, and thus obtain the praise of men.
For I do not think it lawful, that I who was one of his familiars, should be silent concerning his life; and should not, according to my utmost ability, relate such particulars concerning him as are true, and which perhaps ought to be published in preference to others. And indeed by such a neglect I shall not perhaps obtain the esteem and honour of mankind, who will not entirely ascribe my conduct to the desire of avoiding ostentation, but will suppose I avoided such a design from indolence, or some, more dreadful disease of the soul. Incited, therefore, by all these considerations, I have taken upon me to relate some illustrious particulars of this philosopher, since they are almost infinite, and may be depended on for their undoubted reality.
I shall begin therefore not according to the usual manner of writers, who are accustomed to distribute their discourse into chapters; but I consider that the felicity of this blessed man ought, with the greatest propriety, to be placed as the foundation of this treatise. For I regard him as the most happy of those men who were celebrated in former ages; I do not say happy only from the felicity of wisdom, though he[3] possessed this in the highest degree of all men; nor because he abundantly enjoyed the goods of an animal life; nor again on account of his fortune, though this belonged to him in a most eminent degree, for he was supplied with a great abundance of all such things as are called external goods: but I call him happy, because his felicity was perfect, complete in all parts, and composed from each of the preceding particulars. Having then in the first place distributed[41] virtues according to their kinds into natural, moral, and political, and also into those of a sublimer rank, which are wholly conversant with purification and contemplation, and are therefore called Cathartic and Theoretic, and also such as are denominated Theurgic, by which we acquire a similitude with some particular divinity; but omitting such as are superior to these, as beyond the reach of man, we shall begin from such as are more natural, and which are first in the progressions of the human soul, though not first in the nature of things.
This blessed man, then, whose praise is the subject of this treatise, naturally possessed, from the hour of his birth, all those physical virtues which fall to the lot of mankind; the traces of which were manifest in the latest period of his life, and appeared to surround and invest his body after the manner of a tenacious shell. In the first place, he was endued with a singular perfection of sensation, which they denominate corporeal prudence; and this was particularly evident in the nobler senses of seeing and hearing, which are indeed given by the gods to men for the purpose of philosophizing, and for the greater convenience of the animal life; and which remained entire to this divine man through the whole of his life. Secondly, he possessed a strength of body which was not affected by cold, and which was neither weakened nor disturbed by any vicious or negligent diet, nor by any endurance of labours, though it was exhausted day and night, while he was employed in prayer, in perusing the works of others, in writing books himself, and in conversing with his familiars; all which he performed with such expedition, that he appeared to study but one thing alone. But a power of this kind may with propriety be called fortitude of body, from the singular strength employed in such exertions.[4] The third corporeal virtue with which he was endued was beauty, which, when compared with temperance, the authors of these appellations have very properly considered as possessing a similitude of nature. For as we consider temperance as consisting in a certain symphony and consent of the powers of the soul, so corporeal beauty is understood to consist in a certain agreement of the organical parts. He was indeed of a most pleasing aspect, not only because he was endued with this excellent proportion of body, but because the flourishing condition of his soul beamed through his corporeal frame like a living light, with splendors too wonderful for language to explain. And indeed he was so beautiful that no painter could accurately describe his resemblance; and all the pictures of him which were circulated, although very beautiful, were far short of the true beauty of the original. But the fourth corporeal virtue which he possessed was health, which they affirm corresponds to justice in the soul; and that this is a certain justice in the disposition of the corporeal parts, as the other in those of the soul. For justice is nothing more than a certain habit, containing the parts of the soul in their proper duty. Hence, that is called health by physicians, which conciliates the jarring elements of the body into union and consent; and which Proclus possessed in such perfection, that he affirmed he was not ill above twice or thrice, in the course of so long a life as seventy-five years. But a sufficient proof of this is evident from hence, that, in his last illness, he was entirely ignorant what the disorders were which invaded his body, on account of the great rarity of their incursions.
Such then were the corporeal goods which Proclus possessed, and which may be called the forerunners, and as it were messengers, of those forms into which we have distributed perfect virtue. But the first powers and progeny of his soul, which he naturally possessed, previous to instruction, and those parts of virtue with which he was adorned, and which Plato reckons the elements of a philosophic nature[42], must excite the wonder of any one who considers their excellent quality. For he was remarkable for his memory and ingenuity; he was of a disposition magnificent, gentle, and friendly; and a companion,[5] as it were, of truth, justice, fortitude and temperance; and his love of truth was so great, that he never admitted any prudent dissimulation, but hated falsehood vehemently. Indeed it is necessary that he who prosecutes truth, with so much earnestness and sincerity, should be extremely desirous of it from his infancy, since truth is the source of every good, both to gods and men. But that he despised corporeal pleasures, and was an eminent lover of temperance, is sufficiently evident from his great propensity to disciplines, and his desire of every kind of studies; for dispositions of this kind never suffer beastly and illiberal pleasure to dwell it the mind, but are able to excite in the soul, from her own internal operations, sincere pleasure and delight. But it is impossible to say how foreign he was from avarice, so that when a boy he despised the wealth of his parents, though very rich, on account of his incredible love towards philosophy. Hence he was far removed from illiberality, and from the care of lesser concerns, as he was most studious of the universe, and of every thing divine and human. But from such a disposition of the rational soul, having acquired true magnanimity, he considered human life as of no account, and, unlike the multitude, viewed nothing dreadful in death. So that he by no means feared all that rout of molestations which appear terrible to others, and this in consequence of that natural affection which it is proper to call by no other name than that of Fortitude alone. But, from all these virtues, I think it must be evident to those who have not experienced his best of dispositions, that he loved equity from a boy; that he was just and mild, and by no means difficult or unjust in his associations or contracts. To us indeed he certainly appeared modest and elegant, neither avaritious nor illiberal, neither arrogant nor timid.
But will it not be superfluous to mention the goodness and fertility of his ingenuity? Especially among those who know and who have heard, that he was full of the most beautiful disciplines, and who are acquainted with the multitude he produced and published to the world, so that he alone seemed to have drank nothing of the cup of oblivion, as he was endued with a power of memory which was never disturbed, and that which belongs to the oblivious, never happened to him. Besides, he never neglected fresh acquisitions, as if possessing a sufficiency[6] of disciplines; and as one who is merely delighted with their study. But he was most remote from a nature rustic and horrid, and averse from the Muses, and particularly propense to more cultivated endowments: for on account of his singular urbanity and festivity (without transgressing the bounds of true honesty) in his common associations, sacred feasts, and other actions, he allured and charmed his familiars, and always dismissed them more cheerful and pleased.
His mother, therefore, Marcella, lawfully united to his father Patricius, both of the Lycian nation, and excelling in birth and virtue, produced our philosopher, thus endued from the beginning with all these, and other gifts of nature. And[43] Minerva, the tutelar goddess of Byzantium, received him when born, and took care of him as a midwife, she being the cause of his birth in that city: but afterwards she provided for his well-being, when he was numbered among boys and young men; for she appeared once to him in a dream, and exhorted him to the study of philosophy, from whence arose his great propensity to this goddess, as he particularly performed her sacred rites, and cultivated with a greater fury (as I may say) her institutions. Lastly, his parents brought him, when born, into their native country Zanthus, consecrated to Apollo: and I cannot but think that this country happened to him by a certain divine providence; as it was requisite that he, who was to be the prince of all sciences, should be educated under the presiding deity of the Muses. Here, being instituted in the most elegant manners, he pursued moral virtues, and was accustomed to right conduct, and to a declination of its contrary, that which is base.
But at that time the love of the gods, who had attended him from his nativity, manifestly appeared; for being once detained by some disease of body, and it appearing very difficult, and scarcely possible to cure him, there stood at his bed a youth of a more than ordinary[7] appearance, so that even previous to the declaration of his name, he might be considered as[44] Telesphorus or Apollo: but the god proclaiming who he was, and pronouncing his name, touched the head of Proclus (for he stood reclining his head on Proclus’ pillow) and having immediately restored him to health, vanished from his sight. And such was the[45] divine vision, and the divine benevolence at that time exhibited to our youth.
But having, for a short space of time, in Lycia, applied himself to grammar, he went to Alexandria in Egypt, bringing with him very singular moral virtues, by which he excited towards himself the love of the masters resident in that place. Hence Leonas the rhetorician, who derived (as I think) his lineage from Isaurus, and was illustrious among many of that profession, who were then at Alexandria, not only made him a partaker of his studies, but thought him worthy to become his domestic, and ordered that he should be supplied with food, together with his wife and children, no otherwise than if he had been his[46] true son. He likewise took care to procure him the notice of the principal men in Egypt, who being wonderfully delighted with the acumen of the youth’s ingenuity, and with the elegance and integrity of his morals, reckoned him among their greatest friends. But he was also instructed by Orion the grammarian, whose ancestors discharged the sacerdotal office among the Egyptians, and who had made such a progress in the knowledge of his art, that he composed elaborate books on this subject, which he left not without advantage to posterity. He also went to the schools of the Roman preceptors, and made a great progress in that language; for he was at first led to the study of his father’s profession, in which he was illustrious, his employment being the study of law in the royal city. But when it appeared how vehemently the young man was delighted[8] with the study of rhetoric, as he had not yet touched the writings of the philosophers, he both acquired great glory from his acquisitions, and became the admiration of his fellow pupils and masters, on account of the elegance of his discourse, and his celerity in perceiving; and from his exhibiting more the habit and industry of the master, than that of the scholar.
But while he yet frequented the rhetorical school, the sophist Leonas, made him the companion of his journey to Byzantium: which he undertook for the purpose of gratifying his friend Theodorus, who was at that time præfect of Alexandria, and who was a man both polite and magnificent, and a lover of philosophy. But Proclus, though a youth, followed his master more cheerfully in this journey, lest he should be compelled to interrupt his studies. However, that I may speak more truly, a certain good fortune brought him back to the source of his nativity. For, on his return, his tutelar goddess exhorted him to philosophy, and to visit the Athenian schools. But having first returned to Alexandria, and bid farewel to rhetoric, and the other arts which he had formerly studied, he gave himself up to the discourses of the philosophers then resident at Alexandria. But he frequented[47] Olympiodorus, the most illustrious of philosophers, for the sake of imbibing the doctrine of Aristotle; and in mathematical disciplines gave himself to Hero[48], a religious man, and one who was eminently skilful in the proper methods of institution. But these men were so delighted with the manners of the youth, that Olympiodorus wished him to espouse his daughter, whom he had taken care to instruct in philosophy, and Hero committed to him all his religion, and made him his constant companion. But having, on a certain time, heard Olympiodorus, a man who was endued with a great power of speaking, and on account of the celerity of his speech, and the gravity of his subjects, was understood by very few of his auditors, as he was departing with the dismissed multitude, he repeated to his companions all that was said, and almost verbatim,[9] though the discourse was copious; as Ulpianus Gazæus, one of his fellow-disciples informed me, who also consumed not the least part of his life in the study of philosophy. But he likewise learned, with great facility, the writings of Aristotle, pertaining to rational philosophy[49], though the bare reading of them is difficult to those who are engaged in the attempt.
Having therefore, at Alexandria, applied himself to these masters, and enjoyed their confidence in such instruction as they were able to afford, when upon reading together with them a certain author, they appeared to him not to interpret the mind of the philosopher as they ought; conceiving a contempt for these schools, and at the same time being mindful of the exhortation which had been divinely sent to him at Byzantium, he went to Athens, attended by the presiding deities of eloquence and philosophy, and by beneficent dæmons. For that he might preserve the genuine and entire succession[50] of Plato, he was brought by the gods to the guardian city of philosophy, as the circumstances which happened on his first entrance into the city, and all the divine excitations manifestly evince: for they openly presaged, that this gift was sent from the father Apollo, and was a future suffrage of his succession confirmed by divine events. For when his vessel drove to the Pyræum, and it was told to the citizens, Nicolaus, who afterwards flourished in the rhetorical art, but at that time studied under the masters of Athens, descended to the shore as if to an acquaintance, received him for his guest as if he had been a citizen, and brought him to the city; for Nicolaus was also a Lycian. But Proclus, who perceived himself weary from his journey, sat down at the temple of Socrates, though he did not yet know, nor had heard that Socrates was worshipped in that place, and requested Nicolaus that he would stay there for a short time, and, if possible, procure him some water, as he said that he was exceeding thirsty.[10] Immediately Nicolaus, from that very consecrated place, brought him some water; for the fountain belonging to the statue of Socrates was not far distant. But while he was drinking, Nicolaus, for the first time, considering the circumstance: This is an omen, says he, because you have sate in the temple of Socrates, and have there first drank the Attic water. Then Proclus rising, and having paid due reverence to the place, proceeded to the city. But when he came to the tower, the porter who was present at his entrance, and was about to close the gates with bars, said to him, (that I may repeat the words of the man,) “Certainly unless you had come, I should have closed the gates.” And what omen could be more manifest, or could less require the interpretations of[51] Polletes or Melampodes, or such like diviners?
But Proclus, despising the schools of the rhetoricians, though they very much desired his association, as if he had come for that very purpose, met with the prince of philosophers Syrianus[52], the son of Philoxenus. At that time too, Lachares was in the same company, a man much conversant in philosophy, and the companion of Syrianus in his study, but in eloquence he was in as great admiration as Homer in the poetic art. He then was, as I have said, present at the same time. But it was now the evening twilight, and while they were engaged in mutual converse, the sun sate, and the moon made her first appearance after her change: wherefore, having saluted the stranger, they endeavoured to dismiss him, as being a young man, from their company, that they might adore the goddess apart. But he not having proceeded far, beheld also the moon appearing from the same house, and laying aside his sandals, in their presence saluted the goddess. Here Lachares, admiring the confidence of the youth,[11] said, speaking to Syrianus, “This is what Plato[53] divinely affirms of great geniuses; that they either produce great good, or its contrary.” And such, that I may mention a few out of many, were the signatures of divine original, which happened to our philosopher, on his first arrival at Athens.
But Syrianus brought him to the great Plutarch[54], the son of Nestor, who, when he saw the young man, not yet twenty years old, and heard of his love and desire of a philosophic life, he was much delighted, and immediately made him a partaker of his philosophic study, though his age almost forbade such an attempt; for he was then very old. He therefore read to Proclus his commentary on Aristotle’s books on the soul, and on the Phædo of Plato: and this great man exhorted him to commit to writing what he heard, employing the ambition of the youth as an instrument, by telling him, that if he completed those scholia, they would be reported as the commentaries of Proclus. And as he loved the youth very much on account of his inclination to the best studies, he called him his son, and caused him to reside with him as a domestic. But after he saw his temperance, with regard to animal food, he exhorted him not to abstain from animals entirely, but to use them so far as was necessary to the vital energies of the corporeal part. He likewise gave the same advice to Syrianus, concerning the youth’s diet. But he answered the old man, as that divine head (Proclus) informed us: “Suffer him with that frugality to learn what I wish, and then, if he pleases, he may die.” Such was the care of his masters respecting him, in every concern. But the old man lived about two years after the arrival of Proclus; and dying, commended the youth to his successor Syrianus, as also his grandson Archiadas. But Syrianus, when he had received Proclus as his pupil, not only much assisted him in learning, but made him his domestic as to other concerns, and the companion of his philosophic life, having found him such an auditor and successor[12] as he had for a long time sought for; and one who was adapted for the reception of a multitude of disciplines, and divine dogmata.
In a shorter space, therefore, than two years, he read, together with Syrianus, all the works of Aristotle, i. e. his logic, ethics, politics, physics, and theological science. But being sufficiently instructed in these, as in certain[55] proteleia, and small mysteries, Syrianus led him to the sacred discipline of Plato, and this by an orderly progression, and not[56] according to the oracle, with a transcendent foot. And he was careful that he might survey with him true mysteries, with the eyes of his soul, free from material darkness, and with a speculation of intellect refined and pure. Hence Proclus was employed night and day in vigilant energies, and in writing compendiously what he had heard, employing his own judgment in the selection and order. And in consequence of this unwearied assiduity, he made so great a progress in a short time, that by then he was twenty-eight years of age, he composed a multitude of works; and among the rest his very learned and elegant commentaries on the Timæus. But from an institution of this kind, his manners also received a greater ornament, since as he advanced in science he accumulated virtue.
In the original κατὰ τὸ λόγιον, which I wonder Fabricius should translate, quod aiunt, as it is usual with the Platonists, to cite the Zoroastrian oracles exactly in these words, instances of which may be found in Proclus on Plato’s theology; and the very words prove themselves to be a part of an oracle, when attentively considered.]
But he likewise pursued the civil virtues from Aristotle’s political writings, and Plato’s books concerning laws and a republic. However,[13] lest he should be conversant only in the contemplation of these, and should attempt nothing actual, since he was hindered from engaging in public affairs himself, from his being employed in more important concerns, he exhorted Archiadas, who was a religious man, to a political life, at the same time instructing him in its nature and virtues, and explaining to him the methods proper to be observed in the discharge of its duties. And in the same manner as they incite those who run in the race, so he exhorted him to preside in common over the whole of his city, and to confer benefits privately upon each according to all the virtues, but particularly in conformity with the laws of justice. But he excited in reality the emulation of himself in Archiadas, when he exhibited to him his own liberality and magnificence with respect to riches, by bestowing gifts at one time on his friends, and at another time on his kindred, guests, and citizens; proving himself by this means not in the least affected with avarice, and conferring not a little to the good of public concerns. But when dying, he bequeathed that part of his possessions which he did not leave to Archiadas, to his own country, and to Athens. But Archiadas became so great a lover of truth, as well from the company of his own associates as from the friendship of Proclus, that he is never mentioned by our acquaintance, without being at the same time celebrated as the religious Archiadas.
But the philosopher also employed himself in civil consultations among public assemblies, where things pertaining to the republic were discussed; giving the most prudent counsels, conferring with governors concerning equity, and not only exhorting them to an impartial distribution of justice, but in a manner compelling them by philosophical authority. For he had a certain public care of the morals of princes, and not only instructed them in the art of temperate government by his discourse, but also by his own example through the whole of his life; since he was, as it were, the exemplar of temperance to the rest. But he gave a specimen of civil fortitude perfectly Herculean: for since at that time there was, as it were, a sea of troubles upon him, and mighty waves of stormy employments were roused by adverse winds against his upright life, he conducted himself, though in danger, with gravity, and an unshaken constancy.[14] And when he was once very much molested by the improbity of some violent men, which was both pernicious and dangerous to himself, he undertook a journey into Asia, which contributed greatly to his own advantage: for as he was not unskilful in the more ancient rites of that place, which he yet preserved, a divine power afforded him this occasion of departure. Hence, as he well knew the whole of their concerns, he taught them more accurately in things pertaining to the gods, if they happened to have neglected any thing through a long interval of time. And while he was engaged in all these employments, and lived in a correspondent manner, he was so concealed from the multitude that he even excelled the Pythagoreans, who keep with unshaken constancy this precept of their founder, λάθε βιώσας, live concealed. But having passed a year only in the parts of Lydia, he returned to Athens, under the providential protection of the presiding goddess of philosophy. And thus fortitude was perfected in our philosopher, first by nature, then by custom, and afterwards by science and the consideration of causes. Besides this, he exhibited in another manner his politic habit practically, by composing letters for noblemen; and by this means procuring good to entire cities. But of this I have a sufficient testimony from those on whom they were bestowed, as well Athenians as Argives, and others of different nations.
But he likewise much promoted and increased literary studies, demanding of princes rewards for the preceptors, according to their several deserts. Nor did he undertake this rashly, nor with any interested views, but he compelled them (as he considered it a matter of great moment) to be diligent in their profession, interrogating and discoursing with them respecting every particular: for he was a judge sufficiently instructed in the employments of them all. And if he ever found any one negligent in his profession, he sharply reproved him; so that he appeared very vehement and ambitious, because he was both willing and able to give a just determination on every subject: and he was indeed a lover of glory. But this was not a fault in him, as in most, because it alone regarded virtue and goodness. And, perhaps, without an energy of this kind, nothing great and excellent would ever subsist in the human mind. But he was in this[15] respect vehement: this I will not deny. Yet, at the same time, he was gentle; for he was easily pleased, and demonstrated in a moment that his anger was as pliable as wax. For, almost at the same time, he was (as I may say) wholly transported in reprehension, and with a desire of becoming subservient to their interest, and that he might intercede with princes in their names; being moved with a certain natural conjunction of soul, and, as it were, sympathy of grief.
And here, I very opportunely recollect a peculiar example of his natural sympathy of soul with others: nor do I think the like was ever related of any other man. For, notwithstanding he was unmarried, and had no children (because he was not desirous of such connections, but remained free from them all, though many noble and rich alliances were offered him), yet his care of all his familiars and friends, and of their wives and children, was as great as if he had been some common father, and the cause of their birth; for he bestowed a singular attention on the life of each. And whenever any one of them was detained by any disease, he first earnestly supplicated the gods on their behalf with sacrifices and hymns; afterwards he gave a prompt attendance on the sick person himself, convened the physicians, and urged them to make an immediate trial, if they knew of any thing in their art advantageous to the condition of the diseased; and sometimes he produced some singular advice himself, among the physicians; and thus delivered many from imminent dangers. And the greatness of this blessed man’s humanity towards his servants, may be understood by those who desire it, from his will. But of all his familiars, he loved Archiadas and his kindred the most; because, in the first place, their succession was derived from the genus of Plutarch the philosopher; and afterwards on account of that[57] Pythagoric friendship which he maintained with Archiadas, as he was both the companion and preceptor of his studies. And this other kind of friendship, differing from the two already mentioned, appears to have[16] been the most firm and excellent, among these illustrious men. For Archiadas desired nothing, which was not also the wish of Proclus; and on the contrary, the desires of Proclus were the constant wishes of Archiadas.
But having now brought the political virtues, which are inferior to the true ones, to an end, and terminating them in[58] friendship, as their proper bound, we shall now pass to the Cathartic differing from the politic virtues. Indeed, the employment of these last consists in purifying the soul, that so being liberated from the body as much as they are able to effect, it may regard human concerns, and possess a certain similitude with divinity; which is the soul’s best and most exalted end. Yet they do not all liberate after the same manner, but some more, and others less. Since there are certain political purgations which adorn their possessors, even while connected with body, and reduce them to a better condition; bringing under the dominion of reason, anger and desire, and entirely destroying passion and every false opinion: but the Cathartic virtues, which are superior to these, separate entirely from this truly leaden weight of body, and procure an easy flight from mundane concerns. And in these, indeed, our philosopher was studiously employed during the whole of his life, which was devoted to philosophy; since he both taught by his discourses what they were, and after what manner they were preparatory to felicity, and in a particular manner conformed his life to their institutions; performing every thing which could contribute to the separation of his soul, using both night and day prayers, lustrations, and other purifications, as well according to the Orphic as the Chaldaic institutions: and every month he descended, with great diligence, to the sea; and this sometimes twice or thrice. But he was exercised in these, not only in the vigour of his age, but also towards the close of his life; and these customs he observed perpetually, as if they were certain invariable statutes.
But he used meat and drink, and other necessary pleasures, only so far as was necessary to avoid the molestations of disease; for he was in these by much the most frugal, and particularly loved abstinence[17] from animal food. And if at any time he was invited to eat it more vehemently, he was so cautious in its use, that he ate it merely after the manner of a taster. But he purified himself every month by the sacred rites, in honour of the mother of the gods, celebrated by the Romans, and prior to them by the Phrygians: he likewise more diligently observed the unfortunate days of the Egyptians than they themselves; and, besides this, fasted, on certain days in a peculiar manner, on account of the lunar appearances[59]. He likewise instituted a fast on the last day of the month, not having supped the day before. But in what a splendid manner, and with what piety, he celebrated the new moon, and properly observed, with sacrifices, the more illustrious feasts of almost all nations, according to the manner of each country; and how from these he did not, according to the custom of many, take occasion of becoming idle and intemperate, but employed himself in continual prayers, hymns, and the like, his hymns sufficiently evince, which not only celebrate the divinities of the Greeks, but likewise Marna Gazæus, Esculapius Leonteuchus, Ascalonites, and Theandrites, another god much venerated by the Arabians; together with Isis, worshipped by the Philians; and lastly, all the rest which were the subjects of his devotion. For this sentiment was very familiar to this most religious man, that it was proper a philosopher should not be careful in the observance of the rites and institutions of one particular city, nor of certain nations only, but that he should be the general priest of the universe. And thus was he pure and holy, so far as pertains to the virtue of temperance.
[18]
But he declined, as much as possible, pain: and if it ever happened to him, he bore it with gentleness, and diminished it with this view, that his best part might not at the same time be affected with its molestations. And the fortitude of his soul in this respect, was sufficiently evinced in his last illness; for when, at that time, he was oppressed and tormented with the most excruciating pains, he endeavoured to the utmost to mitigate and expel their afflictive invasions. Hence, on such occasions, he often commanded us to repeat certain hymns, which when repeated procured him a remission and cessation of pain. And what is more wonderful, he remembered what he heard of these, though forgetful of almost all human concerns, from the dissolution of his corporeal part continually increasing. For when we began to repeat, he supplied what was unfinished of the hymns, together with many of the Orphic verses; for it was these we were then reciting. Nor was he only thus constant in enduring corporeal evils, but much more so in external unfortunate events, and such as appeared to happen contrary to expectation. So that he would say, concerning particulars of this kind, So it is, such things are usual; which seemed to me, or rather at that time appeared to be, worthy of remembrance, and an evident argument of our philosopher’s magnanimity. But besides this, he restrained anger as much as possible, so that it might either remain free from all excitation, or that at least reason might not consent to its indulgence, but the irrational faculty alone, contrary to his will, might be moderately and lightly excited. And with respect to venereal concerns, he used them in the natural way, but so as that he might not proceed beyond a very moderate and light phantasy, in their indulgence.
And thus the soul of this blessed man, having collected itself from all parts, and retiring into the depths of its essence, departed after a manner from body; while it yet appeared to be contained in its dark receptacle. For he possessed a prudence, not like that of a civil nature, which is conversant in the administration of fluctuating particulars, but prudence itself, by itself sincere, which is engaged in contemplating, and converting itself into itself, without any longer consenting to a corporeal nature. He likewise possessed a temperance free from evil; and which is not even moderately influenced by perturbations,[19] but is abstracted from all affections. And lastly, he acquired a fortitude, which does not fear a departure from body. But reason and intellect having obtained in him a perfect dominion, and the inferior powers of his soul no longer opposing themselves to purifying justice, his whole life was adorned with the divine irradiations of genuine virtue.
Our philosopher, therefore, having most happily absolved this form of virtues, advancing now, as it were, by the highest and most mystical step, he ascended to the greatest and most consummate or telestic virtues; employing for this purpose, the felicity of his nature, and a sciential institution. Hence, being now purified, and the victor of his nativity, and despising the vain Thyrsus-bearers, and boasters of wisdom, he happily penetrated into her profound recesses, and enjoyed the contemplation of the truly blessed spectacles she contains. No longer requiring prolix dissertations, or demonstrations, for the purpose of collecting the science of these, but, with a simple vision and energy of intellect, beholding the exemplar of the divine mind, he obtained a virtue which cannot with sufficient propriety be called prudence, but is more properly denominated wisdom, or something, if possible, still more venerable and divine. But the philosopher energizing, according to this virtue, easily comprehended all the theology of the Greeks and Barbarians, and whatever is shadowed over by the figments of fables, and placed it in a clear light, for the use of those who are willing and able to pursue its latent signification. But having interpreted divinely every thing of this kind, and shewing the symphony between them all; at the same time, investigating all the writings of the ancients, whatever he found in them of genuine wisdom, and approved by general consent, this he judiciously applied to use; but if he found any thing of a different and dissonant nature, this he entirely rejected, as vicious and false. And whatever he met with contrary to wisdom, though endued with a friendly appearance, this he vigorously subverted by a diligent examination. Nor did he employ less force and perspicuity in his association with other men. For he was a man laborious to a miracle; as he often, in one day absolved five, and sometimes more lectures; and writ besides, many verses, often to the number of seven hundred. Besides this, he went[20] to other philosophers, and frequented their company; and again celebrated with them an evening association, ceasing from the labour of writing. And all these employments he executed in such a manner, as not to neglect his nocturnal and vigilant piety to the gods, and assiduously supplicating the sun when rising, when at his meridian, and when he sets.
But he was the parent of many dogmata, which were never known before, both in physics, and in intellectual and more divine concerns. For he first taught, that there was a kind of souls[60], endued with the power of contemplating many forms at once, which he placed, not without great probability, between intellect, collectively, and as it were with one intuition comprehending every thing, and souls, which are alone able to direct their vision to one particular form. And those who are willing to peruse his works will meet with a great variety of dogmata, peculiar to him alone; the relation of which I shall omit, lest I should give a too great extent to my discourse. But he who evolves his writings, will easily perceive that all we have above related of him is most true, and much more if he happens to have known him, to have seen his face, and to have heard him interpreting in the most excellent dissertations, and delivering the Platonic and Socratic dogmata in his yearly schools. Nor did he seem destitute of divine inspiration; for he produced from his wise mouth, words similar to the most white and thick falling snow[61]; so that his eyes emitted a bright radiance, and the rest of his countenance was resplendent with a divine light. Hence, when on a certain time, one Rufinus, a man of a great name in the republic, who was studious of truth, and in other respects worthy of veneration, came to him when he was teaching and interpreting, he perceived that the head of Proclus was surrounded with a light; and when the philosopher had[21] finished his interpretation, Rufinus rising, adored him; and offered to give a public testimony, by oath, of the divine vision which he had observed. And much gold was offered to him, by the same Rufinus, on his return from Asia, having escaped the danger of the war. But Proclus likewise rejected this gift, and was by no means willing to receive it.
But that we may return to our first design, having now discoursed concerning the contemplative wisdom of the philosopher, though in a manner but little suited to its dignity, it remains that we now speak of the justice pertaining to this kind of virtues. For this, unlike that of which we spoke before, is not conversant in distribution, or proportion; but must be equally removed from the kind of self-energizing justice, by which all things are alone directed to the rational soul. For to that, concerning which we now treat, it is alone proper to refer every energy to intellect and the deity, which our philosopher performed in the most exalted manner. For he scarcely rested from his diurnal labours, or refreshed his body with sleep, and perhaps even then was not free from meditation and contemplation. This is certain, that having very speedily roused himself from sleep, as from a certain torpor of the soul, he aspired after the morning, the time of prayer; and lest the greater part of the night, should glide from him without advantage, as he was lying alone in his bed, he either composed hymns, or examined and fortified those dogmata which afterwards, in the day time, he committed to writing.
After a similar manner he pursued that temperance which has an affinity with these virtues, and which consists in a conversion of the soul to intellect, so as not to suffer itself to be touched, nor moved with any other concerns. Lastly, he joined fortitude in alliance with these, by a certain perfect method, zealously aspiring after that liberty which is ignorant of all passion, and which he perceived was natural to the divine object of his contemplation. And thus, through the whole of his conduct, he did not lead the life of a man merely good, to which, as Plotinus says, the political virtues may lead, but leaving this far behind him, he endeavoured to change it for one much more perfect and divine, the life of the gods themselves; since, to become similar[22] to these, and not to virtuous men, was the great object of his contention.
And thus he had rendered virtues of this kind familiar to himself, while he frequented the philosopher Syrianus, and evolved and studied the commentaries of the ancients. But he received from the mouth of his preceptor certain small seeds, as it were, of the Orphic and Chaldaic theology; because he was prevented from hearing the complete interpretation of his master on the Orphic verses. For Syrianus left to the choice of Proclus and one Domninus[62], a philosopher of the Syrian nation, and who afterwards succeeded Syrianus, the exposition of the Orphic writings, or the oracles. But they were by no means unanimous in their choice; for Domninus preferred the interpretation of the Orphic verses, and Proclus that of the oracles. But our philosopher did not perfect his undertaking, because the death of the great Syrianus happened not long after. Having therefore, as I have said, received the outlines from the mouth of his master, he applied himself with the greatest diligence to the written commentaries of Syrianus upon Orpheus; and being assiduously nourished with the copious lucubrations of Porphyry and Jamblichus on the oracles, and similar writings of the Chaldeans, he arrived, as much as is possible to man, to the top of those highest virtues, which the divine Jamblichus was accustomed to call after a truly divine manner, theurgic. He laboured therefore, not without exquisite judgment, in collecting the expositions of philosophers prior to his time; and contracted into one, other Chaldaic hypotheses, and the most excellent of the commentaries on the divine oracles, completing this great work in the space of five years; concerning which this divine vision appeared to him in his sleep. For he saw the great Plutarch approach to him, affirming that he should live so many years as he had composed tetrads or quaternions on the oracles. Afterwards, having collected the number of these, he found they amounted to seventy. But that this was a divine dream, was sufficiently evinced by the last part of his life; for though he lived seventy-five years, as we have mentioned above, yet he had not the perfect use of his powers, in the five last. But his body, though naturally[23] of the best constitution, being debilitated by that hard and scarcely tolerable kind of diet which he used, and by so many frequent labours and fastings, began to languish exactly at his seventieth year, so that he then became much more remiss in all his energies than before. Yet, even at this period, and thus affected, he composed orations and hymns: he also writ some things, and conversed with his friends; but his ancient vigour was wanting in each. Hence the memory of the dream excited his wonder, and he every where said, that he had only lived seventy years. But while he laboured under this infirmity of body, a certain youth, named Hegias, rendered him more alert in the business of interpretation. This young man, who already exhibited from his tender years such egregious signs of all the virtues of his ancestors, was one of that golden chain of philosophers, who had formerly appeared to men; and adhered most diligently to Proclus delivering the Platonic and other theologies. But Proclus, at this advanced period, was not moderately rejoiced in communicating with the young man, his own writings, after he understood that he made cubital advances in every kind of disciplines. And thus we have briefly discoursed concerning the apparatus of the philosopher in the Chaldean oracles.
But I, on a certain time, having read with him the Orphic verses, and heard, among his interpretations, not only the recondite theology which is to be found in Jamblichus and Syrianus, but also, among many other divine men, I requested the philosopher that he would not leave these divine verses also without his explanation: but his answer was, That he had often thought of writing commentaries on Orpheus, but that he had been strongly prohibited in more than one dream. For Syrianus appearing to him in his sleep, had deterred him with threats from the design. Having therefore employed other machines, I intreated that at least he would mark what he principally approved of in the books of his master; which when this best of men had performed, in consequence of my persuasions, and had noted some things in the front of each of Syrianus’s commentaries, we obtained a collection of all these, and by this means scholia, and commentaries of no small bulk; though to accomplish this on the whole of that divine poetry, and on all the Orphic rhapsiodies, was not the intention of Proclus.
[24]
But since, as we have said, his incredible study of these concerns, procured him a greater and more perfect degree of theurgic virtue, hence he no longer remained in the contemplative order, nor contented with either of the twofold properties in divine concerns, exercised intellect and thought alone on the more excellent objects of speculation: but he was careful to obtain another kind of virtues more divine than the former, and separated from the politic mode; for he used the Chaldean assemblies and conferences, and their divine and ineffable concealments. And having comprehended these, he learned the manner of pronouncing and expressing them, with their remaining use, from Asclepigenia, the daughter of Plutarch: for she alone, at that time, preserved the knowledge of the great Orgies, and of the whole theurgic discipline, delivered to her by her father, who received it from Nestor. Besides this, our philosopher also being purified in an orderly manner in the Chaldean lustrations, was an inspector of the lucid hecatic phasmai (or visions) of which he himself makes mention in one of his commentaries. But by moving a certain hecatic sphærula[63], he very opportunely brought down showers of rain, and freed Athens from an unseasonable heat. Besides this, by certain phylacteria, or charms, he stopt an earthquake, and had thoroughly tried the energies of a divining tripod, having learned from certain verses concerning its defect. For when he was in his fortieth year, he thought in a dream, that he repeated to himself, the following verses:
[25]
And in the beginning of his forty-second year, he appeared to himself to pronounce these verses, with a loud voice:
Besides, he clearly perceived that he belonged to the Mercurial series; and was persuaded from a dream that he possessed the soul of[64] Nicomachus the Pythagorean.
Indeed, if I were willing to be prolix, I could relate many theurgical operations of this blessed man; from the infinite number of which,[26] I will only relate one in this place of a very wonderful nature. Asclepigenia, the daughter of Archiades and Plutarch, but the wife of Theagenes, from whom I have received many benefits, while she was yet a girl, and was nourished by her parents, fell into a disease, grievous, and incurable by the physicians. And Archiades, who had reposed in her alone the hope of his race, was deeply afflicted with her condition. But the physicians despairing of her recovery, the father fled to his last anchor, Proclus the philosopher, which he was accustomed to do in affairs of the greatest moment, considering him as his best preserver, and earnestly intreated him to intercede by his prayers with the god for his daughter, whose condition was well known to our philosopher. Proclus therefore, taking with him Pericles[65] the Lydian, a man well deserving the name of a philosopher, went to the temple of Esculapius[66], that he might pray to the god for the health of the sick virgin: for the city at that time happily possessed this divinity, and rejoiced in the temple of the saviour god, which was as yet free from the destruction of the Christians. As soon, therefore, as Proclus had prayed after the ancient manner, the girl immediately perceived a great change and alleviation of her disease; for the preserving god had easily restored her to health. The sacred rites being finished, Proclus went to Asclepigenia, and found her delivered from the molestations of disease, and in a healthy condition. But this affair, with many others, was performed privately, so that no traces of it remained to succeeding investigators; and the house in which he resided greatly assisted him in this design. For besides his other fortunes, he enjoyed a most convenient dwelling, which his father Syrianus and his grand-father Plutarch (for so he did not hesitate to call him) had once inhabited; and this was situated near the temple of Esculapius, together with that of the celebrated Sophocles, and of Bacchus, which is next to the theatre, and looks towards, or is at least seen from, the lofty towers of Minerva.
But how much Proclus was loved by the philosophic goddess is abundantly evinced by his philosophic life, which he chose through her persuasions, and that with the great success we have hitherto described.[27] But she clearly demonstrated her affection to Proclus, by the following circumstance. When her image, which had been so long dedicated in the parthenon, or temple, was taken away by those[67] who, without any hesitation, moved out of their places things the most holy, and which ought to be immoveable, there appeared to the philosopher in a dream, a woman of a graceful form, who admonished him to build a temple with great expedition, for, says she, it pleases Minerva, the presiding deity of philosophy, to dwell with you. And how familiar he was with Esculapius, besides what we have mentioned above, may be evinced from his perceiving the presence of the same god in his last illness. For while he was between sleeping and waking, he perceived a dragon creeping on his head, which vision occasioned a remission of his disease, and a mitigation of his pain; so that it is probable he would have been restored to perfect health, if his desire and vehement expectation of death had not prevented his recovery, or his no longer bestowing a diligent attention on his body.
But he also related the following circumstances, (worthy of being remembered) but not without tears, through the sympathy of his mind. For, when a young man, he was afraid lest he should be infested with the gout, which was the disease of his father, and which loves to descend from parents to their children. Nor was he afraid, as it seems, without reason; for prior to that which we have already related concerning him, he was tormented with pains of this kind, when another extraordinary circumstance happened to this blessed man. In consequence of a certain person’s prescription, whom he had consulted, he applied a plaster to his tormented foot, which an unexpected bird flew away with as he was lying on his bed. And this was certainly a divine and salutary symbol to Proclus, and might have persuaded him not to be afraid of this calamity in future. But he, as I have said, was notwithstanding afflicted with the dread of this disease; he therefore supplicated the healing god concerning this, and intreated him to afford him a more evident token of his will: and after this he saw in his sleep (it is bold indeed to conceive such a circumstance in the mind, but we must dare, nevertheless, nor dread to bring truth[28] to light) Esculapius approaching to him, and accurately contemplating his leg, nor disdaining, through his great philanthropy to embrace his knee. Hence, in consequence of this vision, Proclus was, through the whole of his life, free from the apprehensions of this disease, and was never more tortured with this kind of pains.
Again, the god who is worshipped by the Adrotteni, did not less conspicuously evince his great familiarity with this friend of the gods; for, more than once, the god benevolently presented himself to the sight of Proclus, frequenting his temple. And when he was doubtful, and wished to know what god or gods resided and were worshipped in that place, because the inhabitants were of different opinions in this affair, some believing that the temple of Esculapius was there, persuaded of this by various signs, as voices are certainly said to be heard in that place, and a table is consecrated to the gods, and oracles are given concerning the recovery of health, and those who approach are miraculously delivered from the most grievous dangers of life. Others, on the contrary, think that the Dioscuri reside in that place, because there have been those who saw in the way tending towards Adrotta, two young men of the most beautiful form, and riding with great celerity on horseback; at the same time declaring, that they hastened to the temple. They add besides, that the countenance of these was indeed human, but that they immediately gave evidence of a more divine presence; for when the men were arrived at the temple, the above mentioned youths appeared to them, making no enquiry concerning the affair, and occupied in the sacred concerns; but presently after, withdrew themselves from their sight. As the philosopher, therefore, was in doubt concerning these divinities, and did not discredit the relations, having requested the gods who inhabited that place, that they would condescend to manifest who they were; a god appeared to him in a dream, and clearly spoke to him as follows: What! Hast thou not heard of Jamblichus teaching concerning, and celebrating those two, Machaon and Podalirius? And besides this, the god condescended to afford so great an instance of benevolence to this blessed man, that he stood after the manner of those who bestow encomiums on others in the theatres, and with a clear voice, and composed habit, extending his right hand, did not hesitate to exclaim, (that I may[29] relate the words of the god,) Proclus the ornament of the city. And what could possibly be a greater testimony of this blessed man’s friendship with divinity? But he, indeed, in consequence of a most remarkable sympathy, by which he was united with the gods, could never refrain from tears when he mentioned this affair to us, and related the divine encomium of himself.
Indeed, if I were willing to pursue every particular in like manner, and to relate his familiarity with the Hermetic Pan, together with the great benevolence and manifold assistance which that divinity condescended to afford Proclus at Athens, and of that perfectly singular kind of felicity which he obtained from the mother of the gods, and in which he was accustomed especially to triumph and rejoice; I should perhaps seem to many readers, to be rash in my assertions, and to others, the author of things perfectly incredible. For many and great were the daily instances of this goddess’s benevolence towards him, in words and actions, which are both innumerable and unheard of, and concerning which, I do not at present retain an accurate remembrance. But if any one is desirous of knowing how great he was in these, he must evolve his book concerning the mother of the gods, from which he will understand, that it was not without divine assistance he produced all the theology of that goddess into light; as likewise, whatever is acted or affirmed concerning the same in the fables of Athis, which he has explained after a philosophical manner, that vulgar ears might afterwards cease to be disturbed, on perceiving the lamentations and other obscure ceremonies with which her mysteries are celebrated.
After having, therefore, run through the theurgic virtue of Proclus, and its energies, and the happy circumstances which befell him, respecting its operations, and having shewn, that he did not less excel in every kind of virtue, and that he was a man such as mortals have not beheld for a long period of time, it remains that we now bring our discourse concerning him to a conclusion: for we are not now at the beginning of our narration, nor does the half of the whole remain to us, according to the proverb, but the whole itself is now perfect and complete. Since having begun from the felicity of the philosopher, and proceeded in its exemplification, our discourse now returns[30] to it again. For we have explained the great goods, and providential exertions, which were granted to this most excellent man from the gods, and have shewn their prompt attention to his prayers, the divine visions which he enjoyed, and the help and solicitude which the gods testified towards him. We have likewise explained his prosperous fate, and propitious fortune, his country, parents, the good habit of his body, his masters, friends, and other external advantages; each of which we have shewn to have been far greater and more splendid in him than in other men; and have likewise diligently enumerated such things as cannot be reckoned amongst outward allurements, but entirely depended on his will, such as are the upright and illustrious deeds of his soul, according to universal virtue. And thus we have summarily demonstrated that his soul arrived in reality at the summit of the most consummate virtue, and was happily established in a perfect life, by human and divine goods of every kind.
But that the lovers of more elegant studies way be able to conjecture from the position of the stars under which he was born, that the condition of his life, was by no means among the last or middling classes, but ranked among the highest and most happy orders, we have thought fit to expose in this place, the following scheme of his nativity[68].
| ☉ | 16° | 26’ | ♒ |
| ☽ | 17 | 29 | ♊ |
| ♄ | 24 | 23 | ♉ |
| ♃ | 24 | 41 | ♉ |
| ♂ | 29 | 50 | ♐ |
| ♀ | — | 23 | ♓ |
| ☿ | 4 | 42 | ♒ |
| Horos. | 8 | 19 | ♈ |
| Mid. Heaven. |
4 | 42 | ♑ |
| ☋ or the head of the dragon. | |||
| 24 | 33 | ♏ | |
| The new moon preceding his birth. | |||
| 8 | 51 | ♒ | |
[31]
But Proclus departed from this corporeal life, in the one hundred and twenty-fourth year after the government of Julian, on the seventeenth day of the Attic Munichion, or the April of the Romans. Nicagoras, the junior, being at that time the Athenian archon. The dead body was taken care of according to the Athenian rites, as he himself while living had directed. And if that diligent attention which is due to the deceased, was ever paid by any one, it was certainly bestowed by this most blessed man. For he did not neglect any particular of the accustomed ceremonies, but every year, on certain days, visited the sepulchres of the Athenian heroes and philosophers, and besides this sacrificed himself, and not through the medium of another, to the manes of his friends and familiars. And having thus exhibited to each a proper reverence and honour, proceeding into the Academy, he there, in a certain place, pleased one by one the manes of his ancestors and kindred; and shortly after, in another part of the[32] same Academy, he supplicated in common the souls of all philosophers. And these ceremonies being ended, this most excellent man, having chosen a third place, performed sacred rites to all the souls of deceased mankind. The dead body of Proclus, therefore, being disposed of according to his appointment, as we have said, was carried by his friends and buried in the eastern part of the suburbs[69], near to Lycabetus, where also the body of his preceptor Syrianus reposes, who, when he was alive, had requested this of our philosopher, and, in consequence of this, had taken care to procure a twofold receptacle in his sepulchre. But when this most holy man was consulted how he would wish his funeral to be conducted, lest there should be any thing indecent, or without a proper decorum, he desired flutes, with which he was threatened in a dream, and nothing besides. An epigram, consisting of four verses, is inscribed on his tomb, which he composed himself, as follows:
Nor were prognostics wanting in the year prior to his decease, such as an eclipse[70] of the sun, so great that night was produced in the day-time: for the darkness was so profound, that the stars became visible. And this happened when the sun was in Capricorn, in the eastern centre. Besides, the writers of Ephemeride observe that there will be another eclipse of the sun, at the conclusion of the next year. But such like affections of the heavenly bodies are said to portend events on the earth: to us indeed, the eclipse perspicuously signified a privation and, as it were, defection of the illustrious luminary of philosophy.
[33]
And thus much may suffice for the life of the philosopher. It now remains for those who are willing to undertake the labour, to write concerning his disciples and friends. For it appears that many resorted to him from all parts; among which some were only his auditors, but others firm adherents to his doctrine; and, on account of philosophy, his familiars. I could likewise wish that some one, who is more laborious than myself, would give a particular account of his writings. For I have alone delivered these particulars of his life, that I might satisfy my conscience, and might testify that I religiously reverence the soul of Proclus, and his good dæmon. I shall, therefore, add nothing concerning the philosopher’s writings, except that I have always heard him prefer his commentaries on the Timæus of Plato beyond all his works. He likewise vehemently approved of his commentaries on the Theætetus. And he used frequently to say, that if he was endued with despotic power, he would alone preserve, of all the writings of the ancients, the Oracles and the Timæus. For, said he, I would abolish all the rest, and remove them from the present age, because it happens that many are offended, who undertake to read them rashly, and without proper institution.
[34]
Marinus having neglected to give us an account of the writings of Proclus, I thought it would not be unacceptable to the reader, to present him with a catalogue of his works which are still extant; and the most perfect relation I am able of such as are unfortunately lost. In the execution of this design, I shall follow, for the most part, the accurate Fabricius in the order, and critical account of his works; but shall not hesitate to dissent from him in deciding on their philosophical merit: for it is very rare that philology and philosophy are united in the same person, and coalesce in amicable conjunction.
1. Four Hymns. In the preceding life we are informed, by Marinus, that Proclus composed many hymns, in which the divinities, both of Greeks and Barbarians, were celebrated; but unfortunately there are only four preserved, the first of which is to the Sun, the second and third to Venus (which may be found in the Florilegium of Stobus, p. 249. edit. Grotii,) and the fourth to the Muses. They are collected by Fabricius, in the eighth volume of his Bibliotheca Græca; and are most happy specimens of philosophical poetry. Indeed, they bear most evident marks of a mind full of divine light, and agitated with the fury of the Muses; and possess all that elegance of composition for which the writings of Proclus are so remarkable. So that it is very strange Gyraldus should ascribe them to a Hierophant of Laodicæa, of that name; since, as Fabricius observes, Suidas mentions other writings of this priest, but does not speak of him as the author of any hymns. And if he had, these hymns breathe too much of the spirit and manner of Proclus, to be the production of any other.
2. Two Books concerning the useful Parts of Learning, contained in Grammar. Three books on this subject are mentioned by Suidas, and four by Photius; but there are alone extant fragments of two, in the Bibliotheca of Photius; which were published separate by Andrew Schottus, at the end of the syntax of Apollonius Alexandrinus, Francof.[35] 1590. Hanov. 1615. quarto. It appears from these extracts, that Proclus, in this work, not only treats of every kind of verse, but also of the more celebrated poets. And hence Fabricius conjectures, that the short life of Homer, which Leo Allatius published under the name of Proclus, was taken from the first book of this Chrestomathia.
3. Eighteen Arguments against the Christians. The learned Cave, was egregiously mistaken, in supposing that this work, as well as the answer to it by Philoponus, is lost; not considering, probably, that these arguments in defence of the world’s eternity are (as Fabricius well observes) directly against one of the Christian dogmata, the creation of the world. These arguments (except the first, which is lost,) are preserved in the answer of Philoponus; the Greek edition of which was published at Venice, in 1535, folio; and in Latin from the version of Joh. Mahatius, at Lyons, 1557. folio. Simplicius, in his commentaries on the first book of Aristotle de Cœlo, and elsewhere, opposes this work of Philoponus; at the same time, suppressing his name. The arguments are, in my opinion, extremely subtle, and unanswerable; and Philoponus, in his refutation, every where discovers, that he has by no means fathomed the depth of our philosopher.
4. A Commentary on the Timæus of Plato, in five Books. A most admirable work, composed in the flower of his age, when he was twenty-eight years old, according to Marinus. This invaluable treasure, may be said to contain all the wisdom of the highest antiquity: for Proclus every where cites the most celebrated interpreters on the Timæus, such as Adrastus the Peripatetic; Ælianus and Albinus, Platonists; Aristocles, Clearchus, Crantor, Dercyllides; and especially Jamblichus; likewise Longinus, whom he often refutes; Numenius the Pythagorean, and Origen, (different from Adamantius,) together with Plotinus, Porphyry the Platonic, Ptolemy, Severus, and Theodorus Asinæus; but he always prefers the explications of his master Syrianus, before all the rest. Add too, that he every where conciliates the Orphic writings and the Chaldean oracles with the theology of Plato. And with respect to Orpheus in particular, we are indebted to these sublime commentaries for the greatest part of the fragments of that divine poet. He is perpetually on the wing, and rises gradually[36] in elevated conceptions, until his mind, like Homer’s discord, reaches the heavens. His style is at the same time nervous and diffuse, accurate and elegant. We are astonished with the magnificence of his metaphors, delighted with the copious variety of his matter, and filled with a divine light, by the sacred truths he unfolds. This great work, however, unfortunately, scarcely explains a third part of the Timæus; from whence it is probable, as Fabricius well observes, that several books have been lost through the injury of time. It was published in Greek, at Basil, in the year 1556; and is full of mistakes, as is generally the case with the Basil editions of books, so that a more correct edition is greatly to be desired, though at present not much to be expected. On concluding my account of this inestimable work, I find my indignation roused by the following words of Dr. Cudworth, in his Intellectual System, p. 306. “Proclus (says he) had some peculiar fancies and whims of his own, and was indeed a confounder of the Platonic theology, and a mingler of much unintelligible stuff with it.” I must confess, (and I am neither afraid, nor ashamed of the declaration,) that I never found any thing in Proclus, but what by patient thought, accompanied with a sincere and vehement thirst after truth, I have been able to fathom. Had Dr. Cudworth been endued with these requisites, he would doubtless have had equal success; but without them, the sublimest truths will certainly appear to be unintelligible stuff. Besides this consideration is not to be omitted, that a modern priest makes a bad philosopher.
5. On Plato’s Republic. These commentaries, or rather fragments of commentaries, are extant in Greek, at the end of Proclus on the Timæus. Suidas mentions four books of Proclus on Plato’s politics; and some of Proclus’s dissertations on these books, were found (according to Fabricius) in the library of Lucas Holstenius. The chief design of this work seems to be the unveiling the theological mysteries concealed under the fables of Homer, and other divine poets; which Proclus has accomplished (in my opinion) in a most wonderful manner. That Homer, indeed, every where abounds with Egyptian learning, is obvious to every one; but few are acquainted with the profound wisdom which his fables conceal. The latent meaning of most of these is unfolded in the present invaluable, though imperfect[37] work; and he whose mind is sufficiently enlightened by the ancient philosophy, to comprehend the beauty of these illustrations, will receive an additional delight from the study of Homer, which it is impossible to express. An epitome of this work was published in Latin, by the learned Gesner, 1542. 8vo. under the following title: Apologiæ quædam pro Homero, et Arte Poetica, Fabularumque aliquot Enarrationes ex commentariis Procli Lycii Diadochi philosophi Platonici in libros Platonis de Rep. in quibus plurimæ de Diis Fabulæ non juxta grammaticorum vulgus historicè, physicè aut ethicè tractantur, sed Theologicis, ut Gentiles loquntur, ex prima Philosophia rationibus explanantur.
6. On the first Alcibiades of Plato. Ficinus translated parts of this work into Latin, and published them under the title of Procli de Anima ac dæmone, de Sacrificio et Magia, Venice 1497. and 1516. fol. by Aldus; and in a more simple form at Lyons. Fabricius informs us, that the manuscript commentary of Proclus in Greek, but scarcely explaining the half part of the Alcibiades, is to be found in various libraries of France, England, and Italy. Also at Lyons, among the books of Isaac Vossius; and at Hamburgh in the Johannean library. From the specimen given of this work by Ficinus, it appears, like all Proclus’s philosophical writings, to be an invaluable treasury of wisdom; and nothing certainly, reflects greater disgrace on a nation than suffering such monuments of ancient learning and wisdom to lie concealed in colleges, covered with dust, and never consulted.
7. Six Books on Plato’s Theology. A most divine work, in which the philosopher collects into a system the theology dispersed in the writings of Plato, and establishes it by invincible demonstrations. He deduces, in a beautiful and connected series, all the divine orders, from the retreats of ineffable unity; every where connects them by proper mediums, and, after leading us through the long gradation of principles, brings us back again to the original from whence they flowed, and to which they constantly tend. The whole is uncommonly profound and abstruse; and it was not before the third reading, that I could fathom the depth it contains. Fabricius observes, “that it is a subtle and learned work, but from which, you will sooner learn the opinion of Syrianus and Proclus, concerning the deity and divine[38] concerns, than that of Plato. He adds, that it is usual with the Platonists, even from Plotinus, to unite to the doctrine of Plato, a thousand dogmata, foreign from his philosophy, as if Plato, though he did not perceive after this manner, ought certainly so to perceive.” When men mistake their abilities, they always act absurdly, and often dangerously. As a laborious and accurate critic on philological matters, Fabricius merits the highest commendation such attainments can deserve; but when he leaves the beaten road in which nature designed him to walk, and attempts the tractless paths of philosophy, he perpetually stumbles, and often falls on the ground. The wings of philology, like those of the swallow, were never destined for a lofty flight:—it must be the eagle wing of genius, which can alone soar to the sun of philosophy. The Greek and Latin edition of this valuable work, was published at Hamburgh, by Æmilius Portus, 1618, folio.
8. Theological Institutions; or, as it may be called, the Elements of Theology. This admirable work contains two hundred and ten propositions, disposed in a scientific order, and supported by the firmest demonstrations. They begin from super-essential unity, and proceed gradually through all the beautiful and wonderful progressions of divine causes, ending in the self-moving energies of soul. They possess all the accuracy of Euclid, and all the subtilty and sublimity necessary to a knowledge of the most profound theology; and may be considered as bearing the same relation to the Pythagoric and Platonic wisdom, as Euclid’s Elements, to the most abstruse geometry. Patricius, the first Latin translator of this divine work, seems to have been very sensible of the truth of this observation: for he every where carefully distinguishes the propositions from their demonstrations; and adds the word corollary to such consequencies as merit that appellation. His edition was published at Ferraria, 1583. quarto, under the title of Theological Elements. The Greek and Latin edition, is subjoined to Proclus’s six books on Plato’s Theology, Hamburgh 1618. folio.
9. Two Books concerning Motion. This useful work, collected, as Fabricius observes, from the third and following books of Aristotle’s physics, was published in Greek at Basil, 1531, and with the Latin version of one Justus Velsius, a physician, Basil, 1545. octavo. It[39] was likewise translated by Patricius, and is annexed to his version of the Theological Institutions.
10. An Hypotyposis, or Information concerning Astronomical Hypotheses. This work, which Fabricius observes is a compendium of Ptolemy’s Almagest, was published in Greek, at Basil, 1540. quarto; and in Latin by George Valla, folio, 1541. A part of this work, which treats of the use of the astrolabe, Fabricius informs us, is extant in manuscript, in various libraries. The same accurate critic likewise observes, that a small treatise, inscribed Uranodromus, is extant, under the name of Proclus, in some libraries, as in that of Vindobona, and of Oxford, among the Barrocian volumes. The comprehensive variety of Proclus’s genius equally demands our admiration and applause.
11. A small Treatise concerning the Sphere, or Celestial Circles. This little work is an accurate and elegant introduction to astronomy; and is almost wholly taken from the Isagoge of Geminus Rhodius, on the phænomena. The best editions are the Greek and Latin one published at Paris in 1553, quarto; and that of Bainbridge, professor of astronomy at Oxford, London 1620. quarto.
12. A Paraphrase in four Books, on the Quadripartite of Ptolemy. This elegant work must, I should imagine, be an invaluable treasure to the lovers of astrology. It was first published in Greek by Melancthon; and afterwards in Greek and Latin by Leo Allatius, at Lyons Bat. 1654. octavo.
13. Four Books, on the first Book of Euclid’s Elements. For an account of this work, see the introduction, and the following sheets, in which it speaks for itself, in an English dress.
14. A Commentary on Hesiod’s Works and Days. This work contains a valuable moral explanation of this great poet’s meaning; and Fabricius justly observes, that he is often assaulted without occasion, by the petulant jeers of that vain man Joh. Tzetzes. The best edition of this work is that of Daniel Heinsius, Lugd. Bat. 1603. quarto.
15. Fabricius informs us, that in some manuscripts, as in the Vindobonensian and Barrocian, a small treatise is usually ascribed to Proclus, entitled Epistolic Characters; and is prefixed to the Epistles of Phalaris and Brutis, and published under the name of Libanius, in[40] Greek, with the version of Casp. Stibilinus, Commelin. 1597, octavo. But it is doubtful whether Proclus is the genuine author of this work: from the title, I should suppose the contrary. And thus much for an account of those writings of Proclus which have escaped the ravages of time, and have been fortunately exposed to public inspection: it now remains that we relate such inestimable works of this philosopher, as are yet preserved in shameful concealment; or are utterly lost in the ruins of antiquity.
16. On the Alcibiades of Plato. See num. 6.
17. On Plato’s Politics. See num. 5.
18. On Plato’s Parmenides. A commentary, in seven books; the last of which was not completed by Proclus, but by Damascius. From occasional fragments, which have been published of this commentary, it appears to be a most divine work; and indeed it cannot be otherwise, if we consider it as the production of one of the greatest philosophers, on the most sublime and profound of all Plato’s Dialogues. It is dedicated to Asclepiodotus, a physician and philosopher, and is not only extant in Greek MS. in the library of the German emperor, according to Lambecius, lib. vii. p. 41. but also in Latin, from the unpublished version of one Antonius Hermannus Gogava, as the same Lambecius informs us, p. 41. Four books of this work are extant in Greek, in the Bodleian library at Oxford; and it is much to be lamented that Thomson did not publish these, instead of his trifling edition of the Parmenides. Fabricius likewise informs us, that Livius Galantes mentions his having found six of these books in some of the Italian libraries. They are also extant in the Medicæan library of the great Etruscan commander.
19. On the Cratylus of Plato. We have already observed, in the dissertation on the Orphic theology, p. 105. what a great treasure of ancient mythology, must be contained in this work; but there is little hope of its ever emerging from the obscurity of public libraries. It is[41] extant in Greek, not only in the Italian libraries, but also among the manuscript books of Isaac Vossius.
20. Uranodromus. See above, num. 10.
21. Ten Doubts concerning Providence, in one Book. Philoponus mentions this work, in his second book against Proclus on the eternity of the world; and a Latin version of it is extant by one William de Morbeka, in the Johannean library of Hamburgh. Extracts from this translation are preserved by Fabricius, in his Greek Library; and they are in every respect worthy of the genius of Proclus.
22. Concerning Providence and Fate, and that which is in our Power, one Book. This work is dedicated to one Theodorus, a mechanist; and is extant in the Latin translation of the same Morbeka, in the Greek Library of Fabricius. The translation is for the most part barbarous, but is, however, sufficiently legible to discover that it is a most valuable treatise, replete with the usual elegance, subtilty, and sublimity of our philosopher.
23. Concerning the Hypostasis, or Subsistence of Evil. This book is extant in Latin, in the Johannean library; and fragments of it are preserved by Fabricius, in his Greek library. It is to be regretted, that Fabricius did not preserve the whole in that excellent philological work.
24. On the Speech of Diotima, in Plato’s Banquet, concerning the Subsistence of the Beautiful. Fabricius informs us, that this work is distributed into many books; and Holstenius observes, that it is mentioned in a certain scholium of the Medicean copy of Proclus’s commentaries on Plato’s politics; but it is unfortunately no where extant.
25. On the Philebus of Plato; as may be inferred from the narration of Damascius in Photius, p. 550; and Suidas in Marinus. For Damascius relates, that Marinus having composed a commentary on this dialogue, on shewing it to Isidorus for his approbation, that philosopher observed, that those of his master were sufficient; which words Fabricius, with great propriety, applies to the commentaries of Proclus on the Philebus.
[42]
26. On the Theætetus of Plato. This work is praised by Marinus, in the last chapter of the preceding life; and no doubt with great propriety: for this abstruse and sublime dialogue would naturally call forth all the divine fire and elegance of our philosopher.
27. Commentaries on the Enneads of Plotinus. This work is mentioned by Gyraldus, in his second dialogue on ancient poets; by Ficinus on Plotinus; by Philip Labbeus, in his account of MS. books, p. 286; and in the notes of Bullialdus to Theo of Smyrna, p. 224. But also in a certain note prefixed to an ancient manuscript of Jamblichus, on the Egyptian mysteries, to this effect: “The philosopher Proclus, commenting on the Enneads of the great Plotinus, says, that it is the divine Jamblichus who answers the epistle of Porphyry.” This note is in Greek, in the original, and is (in my opinion) of itself sufficient to prove that such a work was once extant, though now unfortunately lost. How much the want of these commentaries is to be regretted, must be deeply felt by every lover of the Platonic philosophy. For the unequalled profundity, and divine mysteries, contained in the writings of Plotinus, could never be more happily illustrated than by the irradiations of such a genius as Proclus.
28. Lectures on Aristotle’s Book Περὶ Ερμηνείας, or concerning Interpretation. This work, it seems, was never published; but Ammonius Hermeas, the disciple of Proclus, has inserted in his valuable commentary on this book all that he could retain in his memory of Proclus’s lectures.
29. Hymns, not a few, see num. 1.
30. Chrestomathea. See num. 3.
31. On the Mother of the Gods, one book, mentioned by Marinus, in the preceding Life.
32. On the Theology of Orpheus. This work is mentioned by Marinus, in the preceding Life, and by Suidas; and its loss must be particularly regretted by all the lovers of recondite theology.
33. Ten Books, on the Chaldean Oracles. This most valuable work is mentioned by Marinus, in the preceding Life, and by Proclus himself on Plato’s Politics, p. 359. It was doubtless not extant at the time when Psellus and Pletho undertook the illustration of a few of[43] these oracles: at least the inconsiderable merit of their commentaries, strongly favours this supposition.
34. A Commentary on the whole of Homer. Suidas. A specimen of the great value of this work may be seen in our philosopher’s commentaries on Plato’s republic. The works of Homer are not only the great fountain of poetry, but likewise of philosophy; and are no less admirable for inspiring the fury of the Muses than for containing the mysteries of the most recondite theology.
35. Concerning the Gods, according to Homer. Had this work been preserved, we should doubtless have been furnished with a defence of the heathen religion, which would have silenced the ignorant clamours of its opponents.
36. The Symphony or Concord of Orpheus, Pythagoras, and Plato. Suidas. Proclus, in his published writings, is every where studious of reconciling the doctrines of these great men, and is always successful in this undertaking. Indeed, the same divine genius seems to have irradiated and inspired these wonderful heroes, but in different ways: in Orpheus it was accompanied with the fire of the Muses; in Pythagoras it shone through the mysterious veil of numbers; and in Plato, combining the preceding modes, it was seen enshrined in awful majesty of thought, clothed with the graces of poetical diction, and resplendent with ineffable light.
37. Two Books on the Theurgic Discipline. Suidas. How much Proclus excelled in this art, may be seen in the preceding Life.
38. Concerning the Oppositions of Aristotle to Plato’s Timæus. This work is mentioned by Proclus in the 3d book of his commentary on the Timæus, p. 226. and seems to have escaped the notice of the accurate Fabricius. Aristotle may, no doubt, in many particulars be reconciled with Plato; but it is also certain, that in some he is perfectly dissonant. And thus much for the Life and Writings of Proclus.
[44]
COMMENTARIES
OF
PROCLUS.
BOOK I.
On the Middle Nature of the Mathematical Essence.
It is necessary that the mathematical essence should neither be separated from the first nor last genera of things, nor from that which obtains a simplicity of essence; but that it should obtain a middle situation between substances destitute of parts, simple, incomposite and indivisible, and such as are subject to partition, and are terminated in manifold compositions and various divisions. For since that which subsists in its inherent reasons remains perpetually the same, is firm and durable, and cannot be confuted, it evidently declares it is superior to the forms existing in matter. But that power of progression which apprehends, and which besides uses the dimensions of subjects, and prepares different conclusions from different principles, gives it an order inferior to that nature which is allotted an indivisible essence, perfectly constituted in itself. Hence (as it appears to me)[71] Plato[45] also divides the knowledge of things which are, into first, middle, and last substances. And to indivisible natures, indeed, he attributes an[46] intelligence, which, in a collective manner, and by a certain simple power, divides the objects of intellectual perception; so that being divested of matter, and endued with the greatest purity, it apprehends things themselves, by a certain unifying perception, and excels the other kinds of knowledge. But to divisible essences, and such as are allotted the lowest nature, and to all sensible beings, he attributes opinion, which obtains an obscure and imperfect truth. But to middle essences (and such are mathematical forms), and to things inferior to an indivisible and superior to a divisible nature, he attributes cogitation. For this, indeed, is inferior to intellect, and the supreme science dialectic; but is more perfect than opinion, and more certain and pure. For it advances by a discursive procession, expands the indivisibility of intellect, and unfolds that which was involved in the unity of intellectual apprehension: but it collects things which are divided, and brings them back to mind. Hence, as knowledges differ among themselves, so the objects of knowledge are distinguished by nature. So that intelligible essences having an uniform subsistence,[47] evidently excel all others. But sensibles are entirely excelled by primary essences: and mathematical natures, and whatever falls under cogitation, are allotted a middle order: for they are excelled by the division of intelligibles; but because destitute of matter, they are superior to sensible natures; and by a certain simple power, they are excelled by the first; but by a certain reason are more exalted than the last. Hence they possess notions of an intellectual essence, which are more manifest than sensibles, but which are, at the same time, only the images of an intellectual nature; and they imitate divisibly the indivisible, and, in a multiform manner, the uniform exemplars of things. And, that I may sum up the whole in a few words, they are placed in the vestibules or entrances of primary forms, and disclose their indivisible and prolific subsistence collected into one, but they do not yet excel the division and composition of reasons, and an essence accommodated to the obscurity of images; nor are they capable of passing beyond the various notions of the soul, endued with a discursive power, and of adhering to intellections perfectly simple, and purified from all material imperfection. After this manner then, is the middle nature of mathematical genera and forms to be understood; as filling up the medium between essences entirely indivisible, and such as are divisible about matter.
[48]
Concerning the common Principles of Beings, and of the Mathematical Essence,[72] bound and infinite.
But it is necessary that, considering the principles of the whole mathematical essence, we should return to those general principles, which pervade through and produce all things from themselves, I mean bound and infinite. For from these two after that cause of one, which can neither be explained, nor entirely comprehended, every other thing, as well as the nature of the mathematical disciplines, is constituted. In the former, indeed, producing all things collectively and separately; but in these proceeding in a convenient measure, and receiving a progression in a becoming order; and in some, subsisting among primary, but in others among middle, and in others again among posterior natures. For intelligible genera, by their simplicity of power, are the first participants of bound and infinite: because, on account of their union and identity, and their firm and stable existence, they are perfected by bound: but on account of their division into multitude, their copious power of generation, and their divine diversity and progression, they obtain the nature of infinite. But mathematical genera originate, indeed, from bound and infinite, yet not from primary, intelligible, and occult principles only; but also from those principles which proceed from the first to a secondary order, and which are sufficient to produce the middle ornaments of[49] beings, and the variety which is alternately found in their natures. Hence, in these also, the reasons and proportions advance to infinity, but are restrained and confined by that which is the cause of bound. For number rising from the retreats of unity, receives an incessant increase, but that which is received as it stops in its progression, is always finite. Magnitude also suffers an infinite division, yet all the parts which are divided are bounded, and the particles of the whole exist finite in energy. So that without the being of infinity, all magnitudes would be commensurable, and no one would be found but what might either be explained by words, or comprehended by reason (in which indeed geometrical subjects appear to differ from such as are arithmetical;) and numbers would be very little able to evince the prolific power of unity, and all the multiplex and super-particular proportions which they contain. For every number changes its proportion, looking back upon, and diligently enquiring after unity, and a reason prior to itself. But bound being taken away, the commensurability and communication of reasons, and one and the same perpetual essence of forms, together with equality, and whatever regards a better co-ordination, would never appear in mathematical anticipations: nor would there be any science of these; nor any firm and certain comprehensions. Hence then, as all other genera of beings require these two principles, so likewise the mathematical essences. But such things as are last in the order of beings, which subsist in matter, and are formed by the plastic hand of nature, are manifestly seen to enjoy these two principles essentially. Infinite as the subject seat of their forms; but bound as that which invests them with reasons, figures, and forms. And hence it is manifest that mathematical essences have the same pre-existent principles with all the other genera of beings.
[50]
What the common Theorems are of the Mathematical Essences.
But as we have contemplated the common principles of things, which are diffused through all the mathematical genera, after the same manner we must consider those common and simple theorems, originating from one science, which contains all mathematical knowledge in one. And we must investigate how they are capable of according with all numbers, magnitudes and motions. But of this kind are all considerations respecting proportions, compositions, divisions, conversions, and alternate changes: also the speculation of every kind of reasons, multiplex, super-particular, super-partient, and the opposite to these: together with the common and universal considerations respecting equal and unequal, not as conversant in figures, or numbers, or motions, but so far as each of these possesses a common nature essentially, and affords a more simple knowledge of itself. But beauty and order are also common to all the mathematical disciplines, together with a passage from things more known, to such as are sought for, and a transition from these to those which are called resolutions and compositions. Besides, a similitude and dissimilitude of reasons are by no means absent from the mathematical genera: for we call some figures similar, and others dissimilar; and the same with respect to numbers. And again, all the considerations which regard powers, agree in like manner to all the mathematical disciplines, as well the powers themselves, as things subject to their dominion: which, indeed, Socrates, in the Republic, dedicates to the Muses, speaking things arduous and sublime, because he had embraced things common to all mathematical reasons, in terminated limits, and had determined them in given numbers, in which the measures both of abundance and sterility appear.
[51]
How these Common Properties subsist, and by what Science they are considered.
But it is requisite to believe, that these common properties do not primarily subsist in many and divided forms, nor originate from things many and the last: but we ought to place them as things preceding in a certain simplicity and excellence. For the knowledge of these antecedes many knowledges, and supplies them with principles; and the multitude of sciences subsist about this, and are referred to it as their source. Thus the geometrician affirms, that when four magnitudes are proportional, they shall be alternately proportional; and he demonstrates this from principles peculiar to his science, and which the arithmetician never uses. In like manner, the arithmetician affirms, that when four numbers are proportional, they shall be so alternately: and this he evinces from the proper principles of his science. For who is he that knows alternate ratio considered by itself, whether it subsists in magnitudes or in numbers? And the division of composite magnitudes or numbers, and in like manner, the composition of such as are divided? For surely it cannot be said that there are sciences and cognitions of things divisible: but that we have no science of things destitute of matter, and which are assigned a more intellectual contemplation; for the knowledge of these is by a much greater priority science, and from these the common reasons of many sciences are derived. And there is a gradual ascent in cognitions from things more particular to more universal, till we revert to the science of that which is, considered as it is, abstracted from all secondary properties. For this sublime science does not think it suitable to its dignity, to contemplate the common properties which are essentially inherent in numbers, and are common to all quantities; but it contemplates the one, and firm essence of all the things which are. Hence, it is the most capacious of all sciences, and from this all the rest assume their own peculiar principles. For the superior sciences always afford the first suppositions of demonstrations to such as are subordinate. But that which is the most perfect[52] of all the sciences, distributes from itself principles to all the rest, to some indeed, such as are more universal, but to others, such as are more particular. Hence, Socrates, in the Theætetus, mingling the jocose with the serious, compares the sciences which reside in us to doves: but he says they fly away, some in flocks, but others separate from one another. For such, indeed, as are more common and more capacious, comprehend in themselves many such as are more particular: but such as being distributed into forms, touch things subject to knowledge, are distant from one another, and can by no means be copulated together, since they are excited by different primary principles. One science, therefore, precedes all sciences and disciplines, since it knows the common properties which pervade through all the genera of beings, and supplies principles to all the mathematical sciences. And thus far our doctrine concerning dialectic[73] is terminated.
What the Instrument is, which judges of the Mathematical Genera and Species.
Let us now consider what that instrument is[74], adapted to the judgment of mathematical concerns; and let us appoint Plato as our guide in this affair, who, in his Republic, divides cognitions separately from such things as are the objects of knowledge; and distributes cognitions in conjunction with things subject to knowledge. For of the things which are, some he ranks among intelligibles, and others among sensibles. And of intelligibles, some are again pure intelligibles, and others subject to cogitation. And of sensibles, some[53] are purely sensibles, but others conjectural. To intelligibles, indeed, which are the first of the four genera, he assigns an intelligible knowledge; but to those which are subject to cogitation, he attributes thought: to sensibles, faith; but to conjecturals, a conjectural or assimilatory power. And he shews, that the assimilatory power has the same proportion to sense as thought to intelligence. For the conjectural power knows the spectres of sensible forms, while they are beheld in water and other bodies, which perspicuously represent their image: since, by their situation in water, they are after a manner, allotted the last seat in the gradations of forms, and truly become the resemblances of resemblances. In like manner, thought beholds the images of intelligibles in a degraded state, fallen from primary simple and indivisible forms, into multitude and division. Hence, a knowledge of this kind, depends on other more ancient hypotheses; but intelligence arrives at that principle which is no longer supposed. If then, mathematical concerns are neither allotted an essence separate from all division and variety, nor that nature which is apprehended by sense, which is obnoxious to many mutations, and is in every proportion divisible, it must be manifest to every one, that they are essentially subject to cogitation: but cogitation presides over these as an instrument adapted to judgment, in the same manner as sense to sensibles, and the assimilatory power to conjecturals. From whence, indeed, Socrates determines that the knowledge of these is more obscure than the first science, but is more evident than the impulsive apprehension of opinion. For in this the mathematical sciences are inferior to intelligence, because they contemplate that which is evolved, and is endued with a power of progression; but they are superior to opinion, by that stability of reasons which they contain, and which cannot be confuted. And they originate from supposition, through a diminution of the first science; but they contain forms independent of matter, from their possessing a knowledge more perfect than that of sensibles. We have therefore determined an instrument adapted to the judgment of all mathematical concerns, i. e. cogitation, according to the mind of Plato; which places itself indeed above opinion, but is excelled by intelligence.
[54]
Concerning the Essence of Mathematical Genera and Species[75].
It now remains, that we consider what subsistence or essence ought to be assigned to mathematical genera and species? Whether we must deduce their origin and subsistence from sensible objects, or from abstraction, or from a collection of such things as are dispersed by parts into one common definition; or must allow them an existence prior to that of sensibles, as Plato affirms, and as the progression of universal being demonstrates? First then, if we affirm that mathematical species are composed from sensibles; whilst the soul from material triangles or circles, forms in herself the trigonic, or circular species, by a kind of secondary generation; I would ask from whence is derived the great certainty and accuracy of definitions? For it must either proceed from sensibles, or from the soul herself. But from sensibles is impossible, for these, in a continual flow of generation and decay, do not for a moment retain an exact sameness of being; and consequently fall far short of the exactness contained in the definitions themselves. It must therefore proceed from the soul, which, by her immaterial nature, procures perfection from the imperfect, accurate[55] subtilty from that which is neither accurate nor subtle, and rekindles the light of ideas from the obscure and unreal objects of sense.
For where shall we find, amongst sensible objects, an indivisible nature, such as that of a point, or a line without the dimension of breadth, or a superficies without depth, or the ever constant proportion of sides, and exact rectitude of angles? For my part, I cannot see where, since all divisible natures are thus mixed and confused together, nothing sincere, nothing free from its contrary, but things every where yielding to separation, as well such as are removed by distance of place, as those which are united together. How then shall we obtain this durable essence for these immoveable natures from the ever fluctuating forms of sense? For whatever derives its existence from moveable beings, must of necessity be mutable and frail. And how shall we gain this perfect accuracy for the stable species, from the inaccurate and imperfect? For whatever is the cause of a conception, always immutable, is itself much more stable than its effect. We must therefore admit the soul to be the generator of these mathematical species and reasons. But if she contains them in herself, as first exemplars, she gives them an essential being, so that the generations are nothing else than propagations of species, which had a prior subsistence in herself: and thus we shall speak agreeably to the sentiments of Plato, and discover the true essence of mathematical entities. But if the soul, though she neither possesses nor received the mathematical reasons prior to the energies of sense, yet fabricates this admirable immaterial building, and generates this fair series of speculations; how can she discern whether her productions are stable and constant, or things which the winds may dissipate, and phantoms rather than realities? What standard can she apply as the measure of their truth? Or how, since she is destitute of their essence, can she generate such a variety of reasons? For from such an hypothesis, we make their subsistence fortuitous, not tending to any scientific bound. Mathematical species are therefore the genuine offspring of the soul: nor does she derive from sensible objects the definitions she frames, but rather the first are propagated from the second; they are the energies of soul, which, as it were, pregnant with forms, delivers her immaterial[56] progeny into the dark and fluctuating regions of matter, as evidences of the permanent duration of her species.
Again, if we collect mathematical reasons from externals, why are not demonstrations composed from sensibles, better than the demonstrations of universal and simple species? For we say, in order to the investigation of any thing sought, that the principles and propositions, should be allied to the conclusions. If then, particulars are the causes of universals, and sensibles the sources of reasoning, why does the boundary of demonstration always refer to that which is more universal, and not to that which is partial and particular? And how can we prove that the essence of intelligibles is more allied to demonstration than the essence of sensibles? For thus they speak[76]: his knowledge is not legitimate, who demonstrates that the isosceles, the equilateral, or the scalene triangle, have angles equal to two right; but he possesses science, properly so called, who demonstrates this of every triangle simply, or of triangle itself. And again, that universals, for the purpose of demonstration, are superior to particulars; that demonstrations concern things more universal; but that the principles from which demonstrations are composed, have a priority of existence, and a precedency in nature to singulars, and are the causes of the propositions they prove. It is very remote, therefore, from the nature of Apodictical sciences, that from converse with things of posterior origin, and from the dark perceptions of sense, they should falsely collect their indubitable propositions. I add farther, that they who affirm this, make the soul of a baser nature than the material species themselves. For if matter derives from nature beings essential, and participating a high degree of entity and evidence; but the soul, by a posterior energy, receives these from sensible objects, and fashions in herself resemblances and images of posterior origin, contemplating vile essences, and abstracting from matter, the forms inseparable from its nature; do they not make the soul more obscure and indigent[57] than matter itself? For matter is the receptacle of forms materialized, as the soul is of species immaterialized. But in this case, matter would be the place of primary beings, and the soul of such as are secondary and subordinate: matter and its forms obtaining the lead in being, and existing as the sources of the subsistence of immaterial forms. Lastly, the material forms would have an essential existence, the others only an intentional denomination. How then can the soul, which is the first participant of intellect, and an intellective essence, and which derives from thence consummate knowledge, and a plenitude of life, become the receptacle of the most obscure species, the lowest in the order of things, and participating the most imperfect existence. But this opinion, which has been sufficiently exploded by others, needs no farther confutation.
If then, mathematical species do not subsist by material abstraction, nor by a collection of those common properties inherent in individuals; nor are at all, in their origin, posterior to sensibles, nor derived in any manner from them: it is necessary that the soul should either deduce them from herself, or from intellect; or lastly, from herself and intellect united. But if from herself alone, Whence do the images of intellectual species arise; whence do they derive their middle nature, linking, as it were, the divisible and indivisible essence together; if they do not participate the fullness of entity from primary essences? Lastly, how, upon this hypothesis, are the first exemplars, paradigms, or ideas, which subsist in intellect, the principles of universals? But if they are derived from intellect alone into the soul, how can the soul remain self-operative, and self-motive, if her inherent reasons flow from an external source, and are regulated by its operations? And in what respect does the soul differ from matter, which is all things in mere dormant capacity, but generates nothing appertaining to material species? It remains, therefore, that the soul deduces these species from herself, and intellect; and that she is the absolute consummation of the forms which originate from intellectual exemplars, but which are allotted from themselves a transition to permanent being. The soul, therefore, is by no means to be compared to a smooth tablet, void of all reasons; but she is an ever-written tablet, herself inscribing the characters in herself, of which she[58] derives an eternal plenitude from intellect. For soul is a certain subordinate intellect, revolving round an intellect prior to herself, formed to its image, and participating its divine irradiations. If then, this superior intellect is all things intellectually, soul will all things animally; if the first exists as the exemplar, soul will be as its image; if as contracted and united in itself, soul as divisible and expanded. And this is what Plato understood, when in his Timæus, he composes the soul of the world from all things, dividing her according to harmonical reasons, and analogies; assigning to her the first principles effective of figures, I mean the right and circular line, and giving an intellectual motion to her inherent circles. All mathematical species, therefore, have a primary subsistence in the soul: so that, before sensible numbers, there are to be found in her inmost recesses, self-moving numbers; vital figures, prior to the apparent, ideal proportions of harmony previous to concordant sounds; and invisible orbs, prior to the bodies which revolve in a circle. So that soul is the prolific abundance of all these, and is another ornament producing herself, and produced from a proper principle, filling herself with life, and at the same time filled from the demiurgus of the universe, is an incorporeal and indistant manner. When, therefore, she produces and unfolds her latent reasons, she then detects every science and virtue. The essence of soul then consists in these species, nor must we suppose her inherent numbers to be a multitude of units, nor her archytipal ideas of divisible forms to be corporeal: but we must conceive all these as subsisting ever vitally, and intellectually, as the exemplars of apparent numbers, figures, reasons and motions. And here we must follow the doctrine of Timæus, who derives the origin, and consummates the fabric of the soul, from mathematical forms, and reposes in her nature the causes of every thing which exists. For the seven bounding terms[77], comprehending the principles of all numbers, lines, planes and solids, pre-exist in soul according to cause. And again, the principles of figures are placed in her essence, according to a demiurgical power. And lastly, the first of all motions, which embraces every other motion in its comprehensive[59] ambit, is co-existent with soul. For the principle of every thing which is moved is a circle, and the circular motion. The mathematical reasons, therefore, which fully consummate the soul, are essential, and self-moving: and the soul, by her cogitative power, diffusing, propagating, and evolving these, from her profound recesses, constitutes all the fair variety of mathematical sciences. Nor will she ever cease to generate, and waken into energy, succeeding species, while she divests her indivisible reasons of their intellectual simplicity. For she previously received all things, after a primary manner; and according to her infinite power, from pre-existent principles, deduces a beautiful series of various speculations.
What the Employments and Powers are of the Mathematical Science, and how far they extend themselves in their Energies.
But, after contemplating the essence of mathematical forms, it is necessary we should recur to that one master-science of these, which we have shewn is prior to a multitude of others, and that we should contemplate what its employment is, what are its powers, and how far it advances in its energies. The employment, therefore, of the whole mathematical science, possessing, as we have before said, the power of cogitation, must not be placed so high as that of intelligence; which is firmly seated in its own stable essence, is perfect, is contained by itself, and in itself continually verges. Nor must it be situated so low as that of opinion and sense, since these cognitions dwell upon external concerns, energize upon them, and do not possess the causes of the objects of their knowledge. But the mathematical science, receives its commencement, indeed, extrinsically from[78] recollection, but ends in the most intimate reasons, residing in the depths[60] of the soul; and is excited, indeed, from things posterior, but arrives by gradual advances at the principal essence of forms. Nor is its energy immoveable, like that of intelligence, nor is it affected with local motion and alteration, like sense, but it revolves with a vital energy, and runs through the ornament of incorporeal reasons, sometimes advancing from principles to such things as are perfected by principles, but at other times yielding in a retrograde progression from conclusions to their forming principles: and sometimes proceeding from things previously known, to such as are the subject of investigation: but at other times, from things placed in the question, to such as precede in cognition. Besides, it does not excel all inquisition, as if it were perfect from itself, like intellect, nor is it perfected from[61] others, like sense, but it proceeds by enquiry to invention, and ascends from the imperfect to perfection. But it likewise possesses twofold powers, one kind of these deducing principles into multitude, and generating the different paths of contemplation: but the other endued with a power of collecting many transitions into proper suppositions. For since it proposes to itself as principles, as well unity, and multitude, as bound and infinite, and such things as are subject to its comprehension, are allotted a middle order, between forms indivisible and every way divisible; with great propriety (I think) the gnostic powers of the whole science of these are essentially twofold. One species indeed, hastens to union, and contracts the expansion of multitude: but the other possesses a power of distinguishing things simple into such as are various, more universals into more particulars, and reasons digested in their principle, into things secondary and multifariously multiplied from these principles. For rising higher from its commencement it penetrates even to such things as are the perfections of sensible concerns, is joined with nature, and demonstrates many things together with natural science. Since ascending from inferiors, it accedes in a certain respect proximate to intellectual knowledge, and touches the contemplation of things primary and divine. And hence, in the limits which flow from its essence, it produces the whole mechanic, optic, and catoptric speculation, together with many other sciences which are inwoven and entangled with sensible concerns, and which operate through their assistance. Besides, in its ascensions from corporeal natures, it derives intelligences indivisible and destitute of matter: and with these it perfects its divisible apprehensions, those cognitions which subsist in progressions, and its own genera and forms: it likewise indicates the truth respecting the gods themselves, and in its peculiar treatises exhibits a contemplation of the things which are. And thus much concerning the employment and powers of the Mathematical Science.
[62]
Concerning the Utility of the Mathematical Science.
But let us now consider the utility of this Science, which extends itself from the most principal to the last cognitions. Timæus, therefore, calls the knowledge of the mathematical disciplines the path of erudition, because, indeed, it has the same proportion to universal science, and the first philosophy, which learning has to virtue. For this last frames our soul to a perfect life, by the possession of worthy manners; but the former prepares our cogitation, and the divine eye of our soul to an elevation from the obscurity of sensible information. Hence, Socrates in the Republic, says, “That the eye of the soul, which is darkened and buried by other studies, can by the mathematical disciplines alone be invigorated, and again excited to the contemplation of that which is, and transferred from resemblances to real beings, from an obscure light to that light which has the power of intelligence, and from a cave, and those bonds which exist in it as the authors of generation, and from material impediments be able to rise to an incorporeal and indivisible essence. For the beauty and order of mathematical reasons, and the firmness and stability of the contemplations they afford, conjoins us with intelligible objects, and perfectly determines us in their essences; which perpetually remain the same, ever shining with divine beauty, and preserving a mutual order without end. But Socrates, in the Phædrus, delivers to us three characters who are elevated from sense, because they fill up and accomplish the primary life of the soul, i. e. the philosopher, the lover, and the musician. But the beginning and path of elevation to the lover, is a progression from apparent beauty, using as excitations the middle forms of beautiful objects. But to the musician, who is allotted the third seat, the way consists in a transition from sensible to invisible harmonies, and to the reasons existing in these. So that to the one, sight is the instrument of reminiscence, and to the other, hearing. But to him who is by nature a philosopher, from whence and by what means is reminiscence the prelude of intellectual knowledge, and an excitation to that which truly is, and to truth itself? For this[63] character also, on account of its imperfection, requires a proper principle: for it is allotted a natural virtue, an imperfect eye, and a degraded manner. It must therefore be excited from itself; and he who is of such a nature, rejoices in that which is. But to the philosopher, says Plotinus, the mathematical disciplines must be exhibited, that they may accustom him to an incorporeal nature, and that afterwards using these as figures, he may be led to dialectic reasons, and to the contemplation of all the things which are. And thus it is manifest, from hence, that the mathematics are of the greatest utility to philosophy. But it is requisite that we should be more explicit, and mention the several particulars to which they conduce, and evince that they prepare the intellectual apprehensions of theology. For whatever to imperfect natures appears difficult and arduous in obtaining the true knowledge of the gods, the mathematical reasons render, by their images, credible, manifest, and certain. Thus, in numbers, they indicate the significations of super-essential properties, but they evince the powers of intellectual figures, in those figures which fall under cogitation. Hence it is, that Plato, by mathematical forms teaches us many and admirable sentences concerning the gods, and the philosophy of the Pythagoreans, using these as veils, conceals from vulgar inspection the discipline of divine sentences. For such is the whole of the Sacred and Divine Discourse[79], that of Philolaus in his Bacchics, and the universal method of the Pythagoric narration concerning the Gods. But it especially refers to the contemplation of nature, since it discloses the order of those reasons by which the universe is fabricated, and that proportion which binds, as Timæus says,[64] whatever the world contains, in union and consent; besides, it conciliates in amity things mutually opposing each other, and gives convenience and consent to things mutually disagreeing, and exhibits to our view simple and primary elements, from which the universe is composed, on every side comprehended by commensurability and equality, because it receives convenient figures in its proportions, and numbers proper to every production, and finds out their revolutions and renovations, by which we are enabled to reason concerning the best origin, and the contrary dissolution of particulars. In consequence of this, as it appears to me, Timæus discloses the contemplation concerning the nature of the universe, by mathematical names, adorns the origin of the elements with numbers and figures, referring to these their powers, passions, and energies; and esteeming as well the acuteness as the obtuseness of angles, the levity of sides, or contrary powers, and their multitude and paucity to be the cause of the all-various mutation of the elements. But why may we not say, that it profits much, and in an admirable manner, to that philosophy which is called Politic, as well by measuring the times of actions as affording the various revolutions of the universe, and numbers convenient to things rising into being; I mean the assimilating, and authors of dissimilitude, the prolific too and the perfect, and the contraries to these; together with orderly and elegant ministers of life, and inelegance; and finally, such numbers as procure fertility and sterility. Which, indeed, the speech of the Muses in the Republic[80] evinces, placing the universal Geometric Number as the author of better and more debased generations, and as the cause of the indissoluble perseverance of good manners, and of the mutation of the best Republics into such as are remote from reason, and are given to affections. For it is sufficiently evident, that it belongs to the whole mathematical discipline to deliver the science of this number which is called geometrical, and not to one particular science, such as arithmetic, or geometry: since the reasons or proportions of abundance and sterility, permeate through all the mathematical disciplines. Again, it is the means of our institution in moral philosophy which it brings to its ultimate[65] perfection, and gives order and an elegant life to our manners. Besides this, it delivers to us figures, and modulations and motions convenient to virtue, by which the Athenian guest wishes those to be instituted and perfected, who are destined to pursue moral virtue from their early youth. Add too, that it places before our view the reasons of virtues, in one manner, indeed, in numbers, in another in figures, but differently in musical symphonies; and lastly, it indicates the excess and defect of vices, by which we are enabled to moderate and adorn our manners. Hence it is, that Socrates, in the Gorgias, accusing Calicles of an inordinate and intemperate life, says to him, “You neglect geometry and geometric equality:” but, in the Republic, he finds out the proportion of tyrannic pleasure to a royal interval, according to a plane and solid generation. But we shall learn what great utility is derived to other sciences and arts from the mathematical science, when we consider that it adds order and perfection to contemplative arts; I mean rhetoric, and all such as consist in discourse. But it proposes to the poetic arts, the reasons of poems in the place of an example, because it presides over the measures existing in these. But to the active arts it determines action and motion, by its own abiding and immoveable forms. For all arts, as Socrates says, in the Philebus, require arithmetic, mensuration, and statics, either in all, or in some of their operations. But all these are contained in the discourses of the mathematical science, and are terminated according to their diversity. For from this science the divisions of numbers, and the variety of dimensions, and the difference of weights are known. The utility, therefore, of the whole mathematical science to philosophy itself, and to other sciences and arts, may be from hence known to intelligent hearers.”
[66]
A Solution of an Objection raised by some against the Utility of the Mathematical Sciences.
But some, who are prone to contradiction through those who wish to subvert geometry, endeavour to destroy the dignity of this science. One part, indeed, depriving it of ornament and good, because it does not discourse on these. But another part[81] affirming that sensible experiments are more useful than the universal objects of its speculation; I mean, that Geodesia (for instance,) or the mensuration of the earth, is preferable to geometry, and vulgar arithmetic to that arithmetic which is conversant with theorems alone: and that nautical astrology is more useful than that which teaches universally, abstracted from any application to sensible concerns. For we are not, say they, made rich by our knowledge of riches, but by using them; nor are we happy by the merely understanding felicity, but by living happily. Hence we must confess that those mathematical sciences, which are conversant with cognition, do not profit human life, and confer to action, but those only which are engaged in exercise. For those who are ignorant of the reasons of things, but are exercised in particular and sensible experiments, are in every respect more excellent, for the purposes of human life, than those who are employed in contemplation alone. Against objections then, of this kind, we shall reply, by shewing the beauty of the mathematical disciplines from those arguments by which Aristotle endeavours to persuade us. We must therefore confess that there are three things which especially cause beauty, both in bodies and souls; I mean, order, convenience, and determination. Since corporeal baseness, indeed, arises from material inordination, deformity, and inconvenience, and from the dominion[67] of the indefinite in the composite body. But the baseness of the soul originates from its irrationality, and inordinate motion, and from its being in a state of discord with reason, and not receiving from thence its proper limitation. Hence, beauty exists even in contraries, by means of order, convenience and determination. But we may behold these in a more eminent degree in the mathematical science; order, indeed, in the perpetual exhibition of things posterior and more various, from such as are primary and more simple; for things subsequent are always annexed to their precedents, the latter ranking as principles, and the former as the first suppositions of things consequent: but convenience is evinced in the mutual consonance of things demonstrated, and in the relation of all of them to intellect, since intellect is the common measure of all science, from which it receives its principles, and to which it converts the learner: but determination is perceived in its perpetually abiding and immoveable reasons, for the objects of its knowledge are not, at times, subject to variation, like those of opinion and sense, but present themselves for ever the same, and are bounded by intellectual forms. If such then, are the principal requisites of beauty, it is evident, that in these sciences that illustrious ornament and gracefulness is found. For how is it possible this should not be the case with a science receiving a supernal illumination from intellect, to which it continually advances, hastening to transfer us from the obscure light of sensible information? With respect to the second objection, we think it proper to judge of its utility, without regarding the conveniencies and necessities of human life. For otherwise, we must confess that contemplative virtue is also useless, which separates itself from human concerns, which it is very little desirous to look down upon and understand. Indeed Socrates, in the Theætetus, affirming this concerning noblemen endued with the prophetic power, says, “that it withdraws them from all regard to human life, and raises their thoughts, properly liberated, from all necessity and use, to the very summit of all true being.” The mathematical science, therefore, must be considered as desirable for its own sake, and for the contemplation it affords, and not on account of the utility it administers to human concerns. But if it is necessary to refer the utility it produces to something different[68] from itself, it must be referred to intellectual knowledge. For it leads us to this, and prepares the eye of the soul for the knowledge of universals, removing and obliterating the impediments arising from the senses, and from corporeal involution. As therefore we call the whole of purgative virtue useful, or the contrary, not regarding the use of the sensible life, but of that which is contemplative, so indeed it is requisite to refer the end of mathematics to intellect, and universal wisdom. Hence its energy is worthy our study, both on its own account, and on account of an intellectual life. But it appears, as Aristotle[82] says, that this science is desirable of itself to its votaries, because though no reward is proposed to its enquirers, yet the mathematical contemplation receives, in a small time, an abundant increase. Besides, this is farther evident from hence, that all men are willingly employed in its pursuit, and wish to dwell on its speculations, omitting every other concern; even those who have, with their lips, as it were, but just touched its utility. And hence it follows, that they who despise the knowledge of the mathematical disciplines, have very little tasted of the pleasures they contain. The mathematics, therefore, are not to be despised because their speculative parts do not immediately confer to human utility, (for the ultimate limits of its progressions, and whatever operates with matter, consider a use of this kind;) but on the contrary we should admire its immateriality, and the good which it contains, considered by itself alone. For when mankind were entirely disengaged from the care of necessary concerns, they converted themselves to the investigation of the mathematical disciplines; and this, indeed, with the greatest propriety. Since affairs familiar to human life in its most imperfect state, and which are immediately connected with its origin, first of all employed the studies of mankind: but, in the second place, those concerns succeeded which separate the soul from generation, and restore its memory of that which IS. After this manner, then, we are engaged in necessaries, before things honourable for their own sakes, on account of their intrinsic dignity and worth; and in things related to sense, before such as are apprehended by the nobler energies of mind.[69] For every origin and life of the soul which is converted into herself, is naturally adapted to proceed from the imperfect to the perfect. And thus much against those who despise the mathematical science.”
A Solution of another Objection of certain Platonists, against the Utility of the Mathematical Sciences.
But, perhaps, some of our own family will here rise up against us, and, proposing Plato as a witness, will endeavour to provoke ruder understandings into a contemptuous disregard of the mathematical disciplines. For they will say, that this philosopher entirely excludes (in his Republic) the mathematical knowledge from the choir of the sciences, and that he accuses it as being ignorant of its own principles, that its very principle is to itself unknown, and its ends and mediums composed from things of which it is ignorant. To these objections they may likewise add whatever other reproaches are there urged by Socrates against this contemplation. In answer then, to the objections of our friends, we shall recall into their memory, that Plato himself perspicuously asserts the mathematical science to be the purgation of the soul, and that it is endued with a power of leading it on high; because, like the Homeric Minerva, it removes the darkness of a sensible nature from the intellectual light of thought, which is better worth saving than ten thousand corporeal eyes, and which not only participates of a mercurial gift, (preserving us from the incantations and delusions of this material abode, which is similar to the fascinating realms of Circe,) but also of the more divine arts of Minerva. He likewise every where calls it by the name of science, and asserts that it is the cause of the greatest felicity to those who are exercised in its contemplation. But I will briefly explain why, in the Republic he takes from it the surname of science: for my present discourse is addressed to the learned. Plato, indeed, in most places, calls all the knowledge (as I may say) of universals by the name of science, opposing it in a division to sense which apprehends only particulars, whether such a mode of cognition is accomplished by art[70] or experience. And in this sense, as it appears to me in the Civil Dialogue, and in the Sophista, he seems to use the name of science; placing likewise the illustrious Sophistic science, which Socrates in the Gorgias, says, is a certain experience: also, the adulatory, and many others, which are experiences, but not true sciences. But again, dividing this knowledge of universals into that which knows causes, and into that which understands without a cause, he thinks that the one should be called science, but the other experience. And hence, to arts he sometimes attributes the name of science, but to experience never. For how (says he in the Banquet) can a thing which possesses no reason be science? All knowledge, therefore, which contains the reason and cause of the things known, is a certain science. Again, therefore, he divides this science which is endued with a power from the cause of knowing, by the peculiarity of its subjects, and he places one, conjectural of things divisible; but the other of such as subsist by themselves, and are ever knowable after the same manner. And according to this division he separates from science, medicine, and every faculty which is conversant with material concerns. But he calls mathematical knowledge, and whatever possesses a power of contemplating eternal objects, by the name of science. Lastly, dividing this science, which we distinguished from arts, he considers one part as void of supposition; but the other as flowing from supposition. And that the one which is void of supposition, has a power of knowing universals: that it rises to good, and the supreme cause of all; and that it considers good as the end of its elevation: but that the other, which previously fabricates for itself definite and determinate principles, from which it evinces things consequent to such principles, does not tend to the principle, but to the conclusion. And hence he asserts, that mathematical knowledge, because it makes use of supposition, falls short of that science which is without supposition, and is perfect. For there is one true science, by means of which we are disposed to know all the things which are, and from which also principles emerge to all sciences; to some, indeed, constituted more proximately, but to others more remotely. We must not say, therefore, that Plato expels mathematical knowledge from the number of the sciences, but that he asserts it to be the second[71] from that one science, which possesses the supreme seat of all: nor must we affirm, that he accuses it as ignorant of its own principles, but that receiving these from the master science dialectic, and possessing them without any demonstration, it demonstrates from these its consequent propositions. For, indeed, he sometimes allows the soul, which is constituted from mathematical reasons, to be the principle of motion: and sometimes he affirms, that it receives its motion from genera which are subject to intelligence. And these variations accord among themselves. For to such things as are moved by another, the soul is a certain cause of motion, but it is not the cause of every motion. After the same manner, the mathematical science is indeed the second from the first of all sciences, and, with reference to it, imperfect: but it is, nevertheless, a science, not as being free from supposition, but as knowing the peculiar reasons resident in the soul, and as bringing the causes of conclusions, and containing the reason of such things as are subject to its knowledge. And thus much for the opinion of Plato respecting mathematics.
But let us now consider what are the things which may be required of a mathematician, and how any one may rightly judge concerning his distinguishing peculiarities. For[83] Aristotle indeed, says, that he who is simply learned in all disciplines, is adapted to judge of all: but that he who is alone skilled in the mathematical sciences, can alone determine concerning the magnitude of reasons inherent in these. It is requisite, therefore, that we should previously assume the terms of judging, and that we should know, in the first place, in what things it is proper to demonstrate generally, and in what to regard the peculiarities of singulars. For many of the same properties reside in things differing in species, as two right angles in all triangles: but many have indeed the same predicament, yet differ in their individuals in a common species, as similitude in figures and numbers. But one demonstration is not to be sought for by the[72] mathematician in these, for the principles of figures and numbers are not the same, but differ in their subject genus. And if the essential accident is one, the demonstration will also be one[84]: for the possession of two right angles is the same in all triangles, and that general something to which this pertains is the same in all, I mean triangle, and a triangular reason. In the same manner, likewise, the possession of external angles to four right ones, not only pertains to triangles, but also to all right-lined figures; and the demonstration, so far as they are right-lined, agrees in all. For every reason brings with it, at the same time, a certain property and passion, of which all participate through that reason, whether triangular, or rectilinear, or universally figure. But the second limit by which a mathematician is to be judged, is, if he demonstrates according to his subject-matter, and renders necessary reasons, and such as cannot be confuted, but are at the same time neither probable, nor replenished with a similitude of truth. For, says Aristotle, it is just the same to require demonstrations from a rhetorician, and to assent to a mathematician disputing probably; since every one, endued with science and art, ought to render reasons adapted to the subjects of his investigation. In like manner also, Plato in the Timæus, requires credible reasons of the natural philosopher, as one who is employed in the resemblances of truth: but of him who discourses concerning intelligibles, and a stable essence, he demands reasons which can neither be confuted nor moved. For subjects every where cause a difference in sciences and arts, since, if some of them are immoveable, others are conversant with motion; and some are more simple, but others more composite; and some are intelligibles, but others sensibles. Hence we must not require the same certainty from every part of the mathematical science. For if one part, after a manner, borders upon sensibles, but another part is the knowledge of intelligible subjects, they cannot both be equally certain, but one must inherit a higher degree of evidence than the other. And hence it is, that we call arithmetic more certain than the science of harmony. Nor must we think it just that mathematics and other sciences should use the same demonstrations; for their subjects afford them no small variety. In[73] the third place, we must affirm, that he who rightly judges mathematical reasons, must consider sameness and difference, what subsists by itself, and what is accidental, what proportion is, and every consideration of a similar kind. For almost all errors of this sort happen to those who think they demonstrate mathematically, when at the same time they by no means demonstrate, since they either demonstrate the same thing as if different in each species, or that which is different as if it were the same: or when they regard that which is accidental, as if it were an essential property; or that which subsists by itself, as if it were accidental. For instance, when they endeavour to demonstrate that the circumference of a circle is more beautiful than a right line, or an equilateral than an isosceles triangle. For the determination of these does not belong to the mathematician, but to the first philosopher alone. Lastly, in the fourth place, we must affirm, that since the mathematical science obtains a middle situation between intelligibles and sensibles, and exhibits in itself many images of divine concerns, and many exemplars of natural reasons, we may behold in it three kinds of demonstration[85], one approaching nearer to intellect, the second more accommodated to cogitation, and the third bordering on opinion. For it is requisite that demonstrations should differ according to the varieties of problems, and receive a division correspondent to the genera of beings, since the mathematical science is connected with all these, and adapts its reasons to the universality of things. And thus much for a discussion of the subject proposed.
[74]
What and how many the Species of the whole Mathematical Science are, according to the Opinion of the Pythagoreans.
But after these considerations, it is requisite to determine concerning the parts of the mathematical science, what, and how many they are. For it is just, after speculating its whole and entire genus, to consider the differences of its more particular sciences, according to their species. The Pythagoreans[86], therefore, thought that the whole mathematical science should receive a fourfold distribution, attributing one of its parts to the how-many, but the other to the how-much; and they assigned to each of these parts a twofold division. For they said, that discrete quantity, or the how-many, either subsists by itself, or must be considered with relation to some other; but that continued quantity, or the how-much, is either stable or in motion. Hence they affirmed, that arithmetic contemplates that discrete quantity which subsists by itself, but music that which is related to another; and that geometry considers continued quantity so far as it is immoveable; but spherics contemplates continued quantity as moving from itself, in consequence of its union with a self-motive nature. They affirmed besides, that these two sciences, discrete and continued quantity, did not consider either magnitude or multitude absolutely, but that alone which in each of these is definite from the participation of bound. For sciences alone speculate the definite, rejecting as vain the comprehension of infinite quantity. But when these wise men assigned this distribution, we must[75] not suppose they understood that discrete quantity which is found in sensible natures, nor that continued quantity which subsists about the fluctuating order of bodies. For, I think, the contemplation of these pertains to the natural and not to the mathematical science. But because the demiurgus of the universe, employed the union, division, and identity of general natures, together with difference, station, and motion, for the purpose of completing the essence of the soul, and composed it from these genera, as Timæus informs us, we must affirm, that cogitation, abiding according to its diversity, its division of reasons, and its multitude, and understanding itself to be both one and many, proposes indeed to itself, and produces numbers, together with an arithmetical knowledge of these: but it provides for itself music according to an union of its multitude, and a communication and junction with itself; and hence it is that arithmetic excels music in antiquity; since, according to the narration of Plato, the demiurgus first divided the soul, and afterwards collected it in harmonical proportions. Again, thought establishing its energy according to the stability which it contains, draws from its inmost retreats geometry, together with one essential figure, and the demiurgical principles of all figures[87]: but, according to its inherent motion, it produces the spherical science. For it is moved also by circles, but abides perpetually the same from the causes of circles. Hence, likewise, geometry precedes spherics, in the same manner as station is prior to motion. But because cogitation itself produces these sciences, not by looking back upon its convolution of forms, endued with an infinite power, but upon the inclosure of bound according to its definite genera; hence they say, that the mathematical sciences take away infinite from multitude and magnitude, and are only conversant about finite quantity. Indeed, intellect has placed in cogitation all the principles both of multitude and magnitude. For since it wholly consists, with reference to itself, of similar parts, and is one and indivisible, and again divisible, educing the ornament of forms, it participates of bound and infinite, from intelligible essences themselves. But it understands, indeed, from its participation of bound, and generates[76] vital energies, and various reasons from the nature of infinite. The intellections, therefore, of thought, constitute these sciences according to the bound which they contain, and not according to an infinity of life; since they bring with them an image of intellect, but not of life. Such then is the opinion of the Pythagoreans, and the division of the four mathematical sciences.
Another Division of the Mathematical Science, according to Geminus.
Again, some think (among whom is Geminus) that the mathematical science is to be divided in a different manner from the preceding. And they consider that one of its parts is conversant with intelligibles only, but the other with sensibles, upon which it borders; denominating as intelligibles whatever inspections the soul rouses into energy by herself, when separating herself from material forms. And of that which is conversant with intelligibles they establish two, by far the first and most principal parts, arithmetic and geometry: but of that which unfolds its office and employment in sensibles, they appoint six parts, mechanics, astrology, optics, geodæsia, canonics, and logistics, or the art of reckoning. But they do not think that the military art, or tactics, should be called any one part of mathematics, according to the opinion of some[88]; but they consider it as using at one time the art of reckoning, as in the numbering of legions; but at another time geodæsia, as in dividing and measuring the spaces filled by a field of camps. As, say they, neither the art of writing, nor the art of healing, are any part of mathematics, though frequently both the historian and physician use mathematical theorems. This is the case with historians indeed, when relating the situation of climates, or collecting the magnitudes and dimensions of[77] cities, or their compass and circuit: but with physicians, when elucidating by ways of this kind, many things in their art. For Hippocrates himself shews the utility derived to medicine from astrology, and almost all who speak of opportune times and places. By the same reason he also, who accommodates his work to tactics, uses indeed mathematical theorems, yet is not on this account a mathematician, although he is sometimes willing that a numerous camp should exhibit a very small multitude, and forms his army according to a circular figure; but sometimes in a quadrangular, quinquangular, or some other multangular figure, when he desires it to appear numerous. But since these are the species of the whole mathematical science, geometry is again divided into the contemplation of planes, and the dimension of solids, which is called stereometry. For there is not any peculiar treatise about points and lines, because no figure can be produced from these without planes or solids. For geometry treats of nothing else in every one of its parts, than that it may constitute either planes or solids: or that when constituted, it may compare and divide them among themselves. In like manner, arithmetic is distributed into the contemplation of linear, plane, and solid numbers. For it considers the species of numbers separate from sensible connections, proceeding from unity, and the origin of plane numbers; I mean of the similar, dissimilar, and solid, even to the third increase. But geodæsia, and the art of reckoning, are divided similarly to arithmetic and geometry, as they do not discourse concerning intelligible numbers or figures, but of such as are sensible alone. For neither is it the office of geodesia to measure the cylinder or the cone, but material masses as if they were cones, and wells as if they were cylinders. Neither does it accomplish this purpose by intelligible right lines, but by such as are sensible, sometimes indeed by a more certain means, as by the solar rays: but at other times by grosser ones, as by a line and perpendicular. In like manner, the reckoner does not survey the passions of numbers by themselves, but as they are resident in sensible objects. From whence he also imposes a name upon these derived from the things which he reckons, calling them μηλίαι, & φιαλίται. Besides this, he does not, admit of any least, like the arithmetician, who receives that minimum, as a genus of[78] relation. For some one man is considered by him as the measure of the whole multitude of men, as unity also is the common measure of all numbers. Again, optics and canonics are produced from geometry and arithmetic. And optics uses the visual rays which are constituted by the rays of the eyes, as lines and angles. But it is divided into that which is properly called optics (because it renders the cause of these appearances, which are accustomed to present themselves to us different from their reality, on account of the different situations and distances of visible objects, as the coincidence of parallel lines, or the appearance of quadrangles as if they were circles); and into universal catoptrics, which is conversant about various and manifold refractions, and is connected with imaginative or conjectural knowledge: as also into that which is called sciography[89], or the delineation of shadows, which shews how appearances in images may seem neither inelegant nor deformed, on account of the distances and altitudes of the things designed. But canonics (music) or the regular art, considers the apparent reasons of harmonies, finding out the sections of rules, every where using the assistance of sense, and, as Plato says, seeming to prefer the testimony of the ears to intellect itself. But to the parts we have hitherto enumerated, mechanics must he added, as it is a certain part of the whole science, and of the knowledge of sensible objects, and of things united with matter. But under this exists the art effective of instruments, which is called (ὀργανoποιητικὴ) I mean of those instruments proper for the purposes of war: such, indeed, as Archimedes is reported to have constructed, resisting the besiegers of sea and land; and that which is effective of miracles, and which is called (θαυματοποιητικὴ.) One part of this constructs with the greatest artifice pneumatic engines, such as Ctesibius and Heron fabricated: but another operates with weights, the motion of which is reckoned to be the cause of inequilibrity; but their station of equilibrity, as Timæus also has determined: and again, another part imitates animate foldings and motions by strings and ropes. Again, under mechanics is placed the knowledge of equilibriums, and of such instruments as are called centroponderants: also (σφαιροποιία) or the[79] art effective of spheres, imitating the celestial revolutions, such as Archimedes fabricated; and lastly, every thing endued with a power of moving matter. But the last of all is astrology, which treats of the mundane motions, of the magnitudes of the celestial bodies, their figures and illuminations, their distances from the earth, and every thing of this kind; assuming many things indeed to itself from sense, but communicating much with the natural speculation. One part of this is gnomonics, which is exercised in settling the dimension of hororary gnomons: but the other is metheoroscopics, which finds out the differences of elevations, and the distances of the stars, and also teaches many other and various astrological theorems. The third part is dioptrics, which ascertains by dioptric instruments of this kind the distances of the sun and moon, and of the five other stars. And such is the account of the parts of the mathematical science, delivered by the ancients, and transmitted to our memory by the informing hand of time.
How Dialectic is the Top of the Mathematical Sciences, and what their Conjunction is, according to Plato.
Let us again consider after what manner Plato, in his Republic, calls dialectic the top of the mathematical disciplines; and what their conjunction is, according to the tradition of the author of the Epinomis[90]. And in order to this we must assert, that as intellect is superior to cogitation, supplying it with supernal principles, and from itself giving perfection to cogitation; in the same manner dialectic also, being the purest part of philosophy, excels in simplicity the mathematical disciplines, to which it is proximate, and with which it is conjoined. Indeed it embraces the complete circle of[80] these sciences, to which it elevates from itself various energies, endued with a power of causing perfection, judgment, and intelligence. And these energies consist in resolving, dividing, defining, and demonstrating; by which mathematics itself, receiving assistance and perfection, invents some things by resolution, but others by composition: and some things it explains by division, others by definition: but collects other subjects of its investigation by demonstration; accommodating, indeed, these ways to its subjects, but using each of them for the purpose of beholding its middle enquiries. From whence indeed, both the resolutions, definitions, divisions, and demonstrations which it contains, are peculiar, and adapted to its nature, and revolve according to the mode of mathematical cognition. Not undeservedly, therefore, is dialectic the vertex as it were, and summit of mathematics. Since it perfects all which mathematics contains of intelligence; renders its certainty free from reprehension, preserves the stability of its immovable essence, and refers what it contains destitute of matter and pure to the simplicity of intellect, and a nature separated from material connections. Besides, it distinguishes the first principles of these sciences, by definitions: exhibits the separations of genera and forms contained under the genera themselves: and besides this, teaches the compositions, which, from principles, produce things consequent to principles: and the resolutions which rise and mount up to things first, and to principles themselves. But with respect to what remains, proportion itself is not to be considered (as Eratosthenes thought it was) as the conjunction of the mathematical disciplines. Since proportion is said to be, and indeed is one of those things common to the mathematics. But in short, many other things besides proportion regard all the mathematical disciplines, which are essentially inherent in the common nature of the mathematics. But as it appears to me, we should say, that there is one proximate conjunction of these, and of the whole mathematical science, which especially embraces in itself, in a more simple manner, the principles of all sciences; which considers their community and difference; teaches whatever is found in these the same; together with what things are inherent in a many, and what in a few. So[81] that to those who aptly learn there is a reversion from many other sciences to this alone[91]. But, dialectic is a conjunction of the mathematical disciplines superior to the preceding; which Plato, as I have already observed, calls in his Republic their vertex: for, indeed, it perfects the whole of mathematics, brings it back to intellect by its powers, shews it to be a true science, and causes it to be certain and obnoxious to no reproof. But, intellect obtains the third order between these conjunctions, which comprehends in itself uniformly all the dialectic powers, contracts their variety by its simplicity, their partition by its indivisible knowledge, and their multitude by its occult union. Hence, intellect itself congregates indeed the involutions and deviations of the dialectic paths, into an intelligible essence, but it collects supernally all the progression of mathematical discourses: and it is the best end both of the elevating power of the soul, and of the energy consisting in cognition. And such are the sentiments declared by me on the present enquiry.
From whence the Name Mathematics originated.
Again, from whence shall we say this name of mathematics, and mathematical disciplines, was assigned by the ancients, and what apt reason can we render of its position? Indeed, it appears to me, that such an appellation of a science which respects cogitative reasons, was not, like most names, invented by indifferent persons, but (as the truth of the case is, and according to report) by the Pythagoreans alone. And this, when they perceived, that whatever is called mathesis or discipline, is nothing more than reminiscence; which does not approach the soul extrinsically, like the images which rising from sensible objects are formed in the phantasy: nor is it adventitious and foreign, like the knowledge consisting in opinion, but it[82] is excited, indeed, from apparent objects, and is perfected within, by thought intimately converted to itself. And when they likewise perceived that though reminiscence might be shewn from many particulars, yet it was evinced in a more eminent manner (as Plato also says[92]) from the mathematical disciplines. For if any one, says he, is led into the descriptions, he will there easily prove that discipline is reminiscence. From whence Socrates also, in the Meno, shews by this method of arguing, that learning is nothing else than the soul’s recollection of her inherent reasons. And this, because that which recollects, is alone the cogitative part of the soul; but this perfects her essence in the reasons of the mathematical disciplines, the sciences of which she previously received into herself, though she does not always energize on their fair variety. Indeed, she contains them all essentially and occultly; but she produces each of them when she is freed from the impediments originating from sense. For sense unites her with divisible objects: the phantasy fills her with forming motions, and appetite bends her to an indulgent and luxurious life. But every thing divisible is an obstacle to our self-conversion. And whatever invests with form, disturbs and offends that knowledge which is destitute of form. And whatever is obnoxious to perturbations is an impediment to that energy which is unimpaired by affections. When, therefore, we have moved all these from the cogitative power, then shall we be able to understand by thought itself, the reasons which thought contains: then shall we become scientific in energy; and unfold our essential knowledge. But whilst we are captive and bound, and winking with the eye of the soul, we cannot by any means attain to a perfection convenient to our nature. Such then is mathesis or discipline: a reminiscence of the eternal reasons contained in the soul. And the mathematical or disciplinative science is on this account particularly denominated that knowledge which especially confers to our reminiscence of these essential reasons. Hence, the business and office of this science[93], is apparent from its[83] name. For its duty is to move the inherent knowledge of the soul; to awaken its intelligence; to purify its cogitation; to call forth its essential forms from their dormant retreats; to remove that oblivion and ignorance, which are congenial with our birth; and to dissolve the bonds arising from our union with an irrational nature. It plainly leads us to a similitude of that divinity who presides over this science, who manifests intellectual gifts, and fills the universe with divine reasons; who elevates souls to intellect, wakens them as from a profound sleep, converts them by enquiry to themselves; and by a certain obstetric art, and invention of pure intellect, brings them to a blessed life. To whom indeed, dedicating the present work, we here conclude our contemplation of the mathematical science.
[84]
BOOK II.
What Part Geometry is of Mathematics, and what the Matter is of which it consists.
In the preceding discourses we have considered those common properties which respect the whole of the mathematical science; and this we have done agreeable to the doctrine of Plato; at the same time collecting such particulars as pertain to our present design. But consequent to this it is requisite that we should discourse on geometry itself, and on the proposed institution of the elements, for the sake of which we have undertaken the whole of the present work. That geometry then, is a part of the whole of mathematics, and that it obtains the second place after arithmetic, since it is perfected and bounded by this, (for whatever in geometry may be expressed and known, is determined by arithmetical reasons) has been asserted by the ancients, and requires no long discussion in the present enquiry. But we also may be able to relate our opinion on this particular, if we consider what place, and what essence its subject matter[94] is[85] allotted among the universality of things. For from a proper survey of this, the power of the science which knows this subject matter, the utility arising from it, and the good acquired by its learners, will immediately appear. Indeed, some one may doubt in what genus of things he ought to place geometrical matter, so as not to deviate from the truth it contains. For if the figures concerning which geometry discourses, exist in sensible natures, and cannot be separated from the dark receptacle of matter; how can we assert that geometry frees us from sensible objects, that it brings us to an incorporeal essence, that it accustoms us to an inspection of intelligibles, and prepares us for intellectual energy? Where shall we ever survey among sensible objects a point without parts, or a line destitute of breadth, or a superficies without profundity, or the equality of lines from the centre to the circumference; or the multangles, and all the figures of many bases, concerning which geometry informs us? Lastly, after what manner can the reasons of such a science remain free from all possible confutation; since, indeed, sensible forms and figures are susceptive of the more and the less, are all moveable and mutable, and are full of material variety; among which equality subsists mixt and confused with its contrary inequality, and into which things without parts have proceeded into partition, and interval, darkened with the shades of matter, and lost in its infinite folds? But if the subjects of geometry are removed from matter, are pure forms, and are separated from[86] sensible objects: they will be all of them, without doubt, void of parts, incorporeal, and destitute of magnitude. For extension, tumor, and interval, approach to forms, on account of the material receptacle in which they are involved, and which receives things destitute of parts, distributed into parts; things void of dimension, extended into dimension; and immoveable natures accompanied with motion. How then, if this is the case, shall we cut a right line, triangle, and circle? How can we speak of the diversities of angles, and the increments and decrements of triangular and quadrangular figures? Or how exhibit the contacts of circles or right lines? For all these evince that the geometric matter consists of parts, and does not reside among indivisible reasons. Such then are the doubts concerning the matter of geometry, to which we may add, that Plato considers the forms of geometry as placed in cogitation; and grants, that we advance from sensibles to forms of this kind, and that we rise from sensibles to intellect, though (as we have previously observed) the reasons subsisting in cogitation are indivisible, are separated by no interval, and subsist according to the peculiarity of the soul. But if reasons are to be rendered agreeable to things themselves, and to the doctrine of Plato, the following division must be adopted. [95]Every universal,[87] and one thing containing many, is either naturally disposed to be thought of in particulars, or to appear such, because it possesses its existence in these; is inseparable from them; is disposed and distributed in them; and together with these is either moved, or firmly and immoveably abides. Or it is adapted to subsist prior to many, and to possess a power of generating multitude, affording to many things images from itself, being furnished with a nature destitute of parts, from the essences which it participates, and raising various participations to secondary natures: or it is disposed to be formed by thought, from the many, to possess a generating existence, and to reside in the last place in the many. For, according to these three modes of subsistence, we shall find, I think, that some subsist before the many, others in the many, and others from the relation and predication which they possess to these. But, that I may absolve all in one word, universal forms being threefold, we shall consider the differences of that form which many participate, which exists in many, and fills particular natures according to its subject matter. Besides this, establishing a twofold order of participants, one subsisting in sensible objects, but the other in the phantasy, (since matter is twofold; one indeed, of things united with sense, but the other of such as fall under the inspection of phantasy, as Aristotle asserts, in a certain place[96]) we must allow that the universal, which is distributed in the many, is likewise twofold. The one, indeed, sensible, as being that which sensible objects participate; but the other imaginative, as that which subsists in the many of the phantasy. For the phantasy, on account of its forming motion, and because it subsists with, and in body, always receives impressions which are both divided and figured. So[88] that whatever is known by it, is allotted a correspondent existence: on which account, Aristotle[97] does not hesitate to call it passive intellect. But if it is intellect, why is it not impassive, and destitute of matter? And if it operates with passion, how can it with propriety be called intellect? For impassivity, indeed, properly belongs to intellect and an intelligent nature: but passivity is very remote from such an essence. But (unless I am deceived) Aristotle being willing to explain its middle nature between cognitions the most primary, and such as are the last, calls it at the same time intellect, because similar to primary cognitions, and passive from that alliance which it possesses with such as are posterior. For first cognitions are indeed destitute of figures and forms; comprehending in themselves, intelligible natures, energizing about themselves, united with the objects of knowledge, and free from all extrinsical impression and passion. But last cognitions exercise themselves through the medium of instruments, are rather passions than energies, admit extrinsical knowledge, and move themselves together with their various subjects. For such (says Plato) are the sensations which arise from violent passions. But the phantasy, obtaining a middle centre in the order of cognitions, is excited, indeed, by itself, and produces that which falls under cogitation: but because it is not separate from body, it deduces into partition, interval, and figure, the objects of its knowledge, from the indivisibility of an intellectual life. Hence, whatever it knows, is a certain impression and form of intelligence. For it understands the circle, together with its interval, void, indeed, of external matter, but possessing intelligible matter. On this account, like sensible matter, it does not contain one circle only: for we behold in its receptacle, distance, together with the more and the less, and a multitude of circles and triangles. If then an universal nature is distributed in sensible circles, since each of these completes a circular figure, and they are all mutually similar, subsisting in one reason, but differing in magnitudes or subjects: in like manner, there is a common something in the circles, which subsist in the receptacle of the phantasy, of which all its circles participate, and according to which they all[89] possess the same form; but in the phantasy they possess but one difference only, that of magnitude. For when you imagine many circles about the same centre, they all of them exist in one immaterial subject and life, which is inseparable from a simple body, which, by the possession of interval, exceeds an essence destitute of parts; but they differ in magnitude and parvitude, and because they are contained and contain. Hence, that universal is twofold, which is understood as subsisting in the many: one, indeed, in sensible forms; but the other in such as are imaginative. And the reason of a circular and triangular figure, and of figure universal, is twofold. The one subsisting in intelligible, but the other in sensible matter. But prior to these is the reason which resides in cogitation, and that which is seated in nature herself. The former being the author of imaginative circles, and of the one form which they contain; but the other, of such as are sensible. For there are circles existing in the heavens, and universally those produced by nature, the reason of which does not fall under a cogitative distribution. For in incorporeal causes, things possessing interval, are distinguished by no intervals: such as are endued with parts, subsist without parts: and magnitudes without the diffusion of magnitude, as on the contrary in corporeal causes, things without parts subsist divisibly, and such as are void of magnitude with the extension of magnitude. Hence, the circle resident in cogitation, is one, simple and free from interval: and magnitude itself is there destitute of magnitude; and figure expressed by no figure: for such are reasons separate from matter. But the circle subsisting in the phantasy, is divisible, figured, endued with interval, not one only, but one and many, nor form alone, but distributed with form. And the circle, in sensible objects, is composite, distant with magnitude, diminished by a certain reason, full of ineptitude, and very remote from the purity of immaterial natures. We must therefore say, that geometry, when it asserts any thing of circle and diameter, and of the passions and affections which regard the circle; as of contacts, divisions, and the like: neither teaches nor discourses concerning sensible forms, (since it endeavours to separate us from these), nor yet concerning the form resident in cogitation, (for here the circle is one, but geometry discourses of many, proposing[90] something of each, and contemplating the same of all: and here it is indivisible, but the geometric circle is divisible); but we must confess, that it considers universal itself; yet as distributed in imaginative circles. And that it beholds, indeed, one circle[98]: and by the medium of another, contemplates the circle resident in the depths of cogitation: but by another, different from the preceding, fabricates the fair variety of its demonstrations. For since cogitation is endued with reasons, but cannot behold them contractedly, separated from material figure; it distributes and removes them, and draws them forth seated in the shadowy bosom of the phantasy, and placed in the vestibules of primary forms; revolving in it, or together with it, the knowledge of these: loving, indeed, a separation from sensibles, but finding imaginative matter proper for the reception of its universal forms. Hence, its intellection does not subsist without the phantasy. And the compositions and divisions of figures are imaginative; and their knowledge is the way which leads us to that essence pursued by cogitation: but cogitation itself, does not yet arrive at this stable essence, while it looks abroad to externals, contemplates its internal forms according to these, uses the impressions of reasons, and is moved from itself to external and material forms. But if it should ever be able to return to itself, when it has contracted intervals and impressions, and beholds multitude without impression, and subsisting uniformly; then it will excellently perceive geometrical reasons, void of division and interval, essential and vital, of which there is a copious variety. And this energy will be the best end of the geometric study; and truly the employment of a Mercurial gift, bringing it back as from a certain Calypso, and her detaining charms, to a more intellectual knowledge; and freeing it from those forming apprehensions with which the mirror of the phantasy is replete. Indeed, it is requisite that a true geometrician should be employed in this meditation, and should establish, as his proper end, the excitation and transition from the phantasy to cogitation alone; and that he should[91] accomplish this by separating himself from intervals, and the passive intellect to that energy which cogitation contains. For by this means he will perceive all things without an interval, the circle and diameter without a part, the polygons in the circle, all in all, and yet every one separate and apart. Since, on this account, we exhibit also in the phantasy, both circles inscribed in polygons, and polygons in circles; imitating the alternate exhibition of reasons destitute of parts. Hence, therefore, we describe the constitutions, the origin, divisions, positions, and applications of figures: because we use the phantasy, and distances of this kind proceeding from its material nature; since form itself is immoveable, without generation, indivisible, and free from every subject. But whatever form contains occultly, and in an indistant manner, is produced into the phantasy subsisting with intervals, divisibly and expanded. And that which, indeed, produces the forms of geometric speculation, is cogitation: but that from which they are produced, is the form resident in cogitation: and that in which the produced figure resides is what is called the passive intellect. Which folds itself about the impartibility of true intellect, separates from itself the power of pure intelligence free from interval; conforms itself according to all formless species, and becomes perfectly every thing from which cogitation itself, and our indivisible reason consists. And thus much concerning the geometric matter, as we are not ignorant of whatever Porphyry the Philosopher has observed in his miscellanies, and whatever many of the Platonists describe. But we think that the present discussions are more agreeable to geometric dissertations, and to Plato himself, who subjects to geometry the objects of cogitation. For these mutually agree among themselves; because the causes, indeed, of geometrical forms, by which cogitation produces demonstrations, pre-exist in demonstration itself: but the particular figures which are divided and compounded, are situated in the receptacle of the phantasy.
[92]
What kind of Science Geometry is.
But let us now speak of that science which possesses a power of contemplating the universal forms participated by imaginative matter. Geometry, therefore, is endued with the knowledge of magnitudes and figures, and of the terms and reasons subsisting in these; together with the passions, various positions and motions which are contingent about these. For it proceeds, indeed, from an impartible point, but descends even to solids, and finds out their multiform diversities. And again, runs back from things more composite, to things more simple, and to the principles of these: since it uses compositions and resolutions, always beginning from suppositions, and assuming its principles from a previous science; but employing all the dialectic ways. In principles, by the divisions of forms from their genera, and by defining its orations. But in things posterior to principles, by demonstrations and resolutions. As likewise, it exhibits things more various, proceeding from such as are more simple, and returning to them again. Besides this, it separately discourses of its subjects; separately of its axioms; from which it rises to demonstrations; and separately of essential accidents, which it shews likewise are resident in its subjects. For every science has, indeed, a genus, about which it is conversant, and whose passions it proposes to consider: and besides this, principles, which it uses in demonstrations; and essential accidents. Axioms, indeed, are common to all sciences (though each employs them in its peculiar subject matter), but genus and essential accident vary according to the sciential variety. The subjects of geometry are therefore, indeed, triangles, quadrangles, circles, and universally figures and magnitudes, and the boundaries of these. But its essential accidents are divisions, ratios, contacts, equalities, applications, excesses, defects, and the like. But its petitions and axioms, by which it demonstrates every particular are, this, to draw a right line from any point to any point; and that, if from equals you take away equals, the remainders will[93] be equal; together with the petitions and axioms consequent to these. Hence, not every problem nor thing sought is geometrical, but such only as flow from geometric principles. And he who is reproved and convicted from these, is convinced as a geometrician. But whoever is convinced from principles different from these, is not a geometrician, but is foreign from the geometric contemplation. But the objects of the non-geometric investigation, are of two kinds. For the thing sought for, is either from entirely different principles, as we say that a musical enquiry is foreign from geometry, because it emanates from other suppositions, and not from the principles of geometry: or it is such as uses, indeed, geometrical principles, but at the same time perversely, as if any one should say, that parallels coincide. And on this account, geometry also exhibits to us instruments of judging, by which we may know what things are consequent to its principles, and what those are which fall from the truth of its principles: for some things attend geometrical, but others arithmetical principles. And why should we speak of others, since they are far distant from these? For one science is more certain than another (as Aristotle says[99]) that, indeed, which emanates from more simple suppositions, than that which uses more various principles; and that which tells the why, than that which knows only the simple existence of a thing; and that which is conversant about intelligibles, than that which touches and is employed about sensibles. And according to these definitions of certainty, arithmetic is, indeed, more certain than geometry, since its principles excel by their simplicity. For unity is void of position, with which a point is endued. And a point, indeed, when it receives position, is the principle of geometry: but unity, of arithmetic. But geometry is more certain than spherics; and arithmetic, than music. For these render universally the causes of those theorems, which are contained under them. Again, geometry is more certain than mechanics, optics, and catoptrics. Because these discourse only on sensible objects. The principles, therefore, of geometry and arithmetic, differ, indeed, from the principles of other sciences; but the hypotheses of these two,[94] alternately differ and agree according to the difference we have already described. Hence, also, with respect to the theorems which are demonstrated in these sciences, some are, indeed, common to them, but others peculiar. For the theorem which says, every proportion may be expressed, alone belongs to arithmetic; but by no means to geometry: since this last science contains things which cannot be expressed[100]. That theorem also, which affirms, that the gnomons of quadrangles are terminated according to the least[101], is the property of arithmetic: for in geometry, a minimum cannot be given. But those things are peculiar to geometry, which are conversant about positions; for numbers have no position: which respect contacts; for contact is found in continued quantities: and which are conversant about ineffable proportions; for where division proceeds to infinity, there also that which is ineffable is found[102]. But things common to both these sciences, are such as respect divisions, which Euclid treats of in the second book; except that proposition which divides a right line into extreme and mean proportion[103]. Again, of these common theorems, some, indeed, are transferred from geometry into arithmetic; but others, on the contrary, from arithmetic into geometry: and others similarly accord with both, which are derived into them from the whole mathematical science. For the permutation, indeed,[95] conversions, compositions, and divisions of ratios are, after this manner, common to both. But such things as are commensurable, arithmetic first beholds; but afterwards geometry, imitating arithmetic. From whence, also, it determines such things to be commensurables of this kind, which have the same mutual ratio to one another, as number to number; because commensurability principally subsists in numbers. For where number is, there also that which is commensurable is found; and where commensurable is, there also number. Lastly, geometry first inspects triangles and quadrangles: but, arithmetic, receiving these from geometry, considers them according to proportion. For in numbers, figures reside in a causal manner. Being excited, therefore, from effects, we pass to their causes, which are contained in numbers. And at one time, we indifferently behold the same accidents, as when every polygon is resolved by us into triangles[104]: but, at another time, we are content with what is nearest to the truth, as when we find in geometry one quadrangle the double of another, but not finding this in numbers, we say that one square is double of another, except by a deficience of unity. As for instance,[96] the square from 7, is double the square from 5, wanting one. But we have produced our discussion to this length, for the purpose of evincing the communion and difference in the principles of these two sciences. Since it belongs to a geometrician to survey from what common principles common theorems are divided; and from what principles such as are peculiar proceed; and thus to distinguish between the geometrical, and non-geometrical, referring each of them to different sciences.
From whence the whole of Geometry originated, how far it proceeds, and in what its Utility consists.
But, beginning still higher, let us contemplate the whole of geometry, from whence it originated, and how far it proceeds in its energies: for thus we shall properly perceive the ornament which it contains. Indeed, it is necessary to understand that it is extended through the universality of things: that it accommodates its animadversions[105] to all beings; and contains in itself the forms of all things: that, according to its supreme part, and which is endued with the highest power of intelligence, it surveys true beings; and teaches by images the properties of divine ornaments, and the powers of intellectual forms: for it contains the reasons of these also in its peculiar contemplations. And it exhibits what figures are convenient to the god, to primary essences, and to the natures of souls. But, according to its middle cognitions, it evolves cogitative reasons; explains and beholds the variety which they contain; exhibits their existence, and inherent passions; as also, their communities and diversities.[97] From which, indeed, it comprehends, in terminated bounds, the imaginative formations of figures, and reduces them to the essential substance of reasons. But, according to the third propagations of cogitative intelligence, it considers nature, and delivers the manner in which the forms of sensible elements, and the powers which they contain, are previously received according to cause, in the reasons themselves. For it possesses, indeed, the images of universal intelligible genera; but the exemplars of such as are sensible: and completes its own essence, according to such things as are subject to cogitation. And through these, as through proper mediums, it ascends and descends to those universals which truly are, and to sensible forms which are in a state of perpetual formation. But always geometrically philosophising concerning the things which are, it comprehends in all the proportions of virtues, the images of intellectual, animal, and natural concerns. And it delivers, in an orderly manner, all the ornaments of republics: and exhibits in itself their various mutations. Such then are its energies arising from a certain immaterial power of cognition: but when it touches upon matter, it produces from itself a multitude of sciences; such as geodæsia, mechanics, and perspective: by which it procures the greatest benefit to the life of mortals. For it constructs by these sciences, war-instruments, and the bulwarks of cities; and makes known the circuits of mountains, and the situations of places. Lastly, it instructs us in measures: at one time of the diversified ways of the earth; and at another, of the restless paths of the deep. Add too, that it constructs balances and scales, by which it renders to cities a sure equality according to the invariable standard of number. Likewise, it clearly expresses, by images, the order of the whole orb of the earth; and by these, manifests many things incredible to mankind, and renders them credible to all. Such, indeed, as Hiero of Syracuse is reported to have said of Archimedes[106], when he had fabricated a ship furnished with three sails, which he had prepared to send to Ptolemy king of Egypt. For when all the Syracusians together, were unable to draw this ship, Archimedes enabled Hiero[98] to draw it himself, without any assistance from others. But he, being astonished, said, From this day, Archimedes shall be believed in whatever he shall affirm. They also report, that Gelo said the same, when Archimedes discovered the weight of the several materials from which his crown was composed, without dissolving their union. And such are the narrations which many of the ancients have delivered to our memory, who were willing to speak in praise of the mathematics: and, on this account, we have placed before the reader, for the present, a few out of the many, as not foreign from our design of exhibiting the knowledge and utility of geometry.
On the Origin of Geometry, and its Inventors.
But let us now explain the origin of geometry, as existing in the present age of the world. For the demoniacal Aristotle[107] observes, that the same opinions often subsist among men, according to certain orderly revolutions of the world: and that sciences did not receive their first constitution in our times, nor in those periods which are known to us from historical tradition, but have appeared and vanished again in other revolutions of the universe; nor is it possible to say how often this has happened in past ages, and will again take place in the future circulations of time. But, because the origin of arts and sciences is to be considered according to the present revolution of the universe, we must affirm, in conformity with the most general tradition, that geometry was first invented by the Egyptians, deriving its origin from the mensuration of their fields: since this, indeed, was necessary to them, on account of the inundation of the Nile washing away the boundaries of land belonging to each. Nor ought it to seem wonderful that the invention of this as well as of other sciences, should receive its commencement from convenience and opportunity. Since whatever is carried in the circle of generation,[99] proceeds from the imperfect to the perfect. A transition, therefore, is not undeservedly made from sense to consideration, and from this to the nobler energies of intellect[108]. Hence, as the certain knowledge of numbers received its origin among the Phœnicians, on account of merchandise and commerce, so geometry was found out among the Egyptians from the distribution of land. When Thales, therefore, first went into Egypt, he transferred this knowledge from thence into Greece: and he invented many things himself, and communicated to his successors the principles of many. Some of which were, indeed, more universal, but others extended to sensibles. After him Ameristus, the brother of Stesichorus the poet, is celebrated as one who touched upon, and tasted the study of geometry, and who is mentioned by Hippias the Elean, as restoring the glory of geometry. But after these, Pythagoras changed that philosophy, which is conversant about geometry itself, into the form of a liberal doctrine, considering its principles in a more exalted manner; and investigating its theorems immaterially and intellectually; who likewise invented a treatise of such things as cannot be explained[109] in geometry, and discovered the constitution of the mundane figures. After him, Anaxagoras the Clazomenian succeeded, who undertook many things pertaining to geometry. And Oenopides the Chian, was somewhat junior to Anaxagoras, and whom Plato mentions in his Rivals, as one who obtained mathematical glory. To these, succeeded Hippocrates, the Chian, who invented the quadrature of the lunula[110],[100] and Theodorus the Cyrenean, both of them eminent in geometrical knowledge. For the first of these, Hippocrates composed geometrical elements: but Plato, who was posterior to these, caused as well geometry itself, as the other mathematical disciplines, to receive a remarkable addition, on account of the great study he bestowed in their investigation. This he himself manifests, and his books, replete with mathematical discourses, evince: to which we may add, that he every where excites whatever in them is wonderful, and extends to philosophy. But in his time also lived Leodamas the Thasian, Archytas the Tarantine, and Theætetus the Athenian; by whom theorems were increased, and advanced to a more skilful constitution. But Neoclides was junior to Leodamas, and his disciple was Leon; who added many things to those thought of by former geometricians. So that Leon also constructed elements more accurate, both on account of their multitude, and on account of the use which they exhibit: and besides this, he discovered a method of determining when a problem, whose investigation is sought for, is possible, and when it is impossible. But Eudoxus the Cnidian, who was somewhat junior to Leon, and the companion of Plato, first of all rendered the multitude of those theorems which are called universals more abundant; and to three proportions added three others; and things relative to a section, which received their commencement from Plato, he diffused into a richer multitude, employing also resolutions in the prosecution of these. Again, Amyclas the Heracleotean, one of Plato’s familiars, and Menæchmus, the disciple, indeed, of Eudoxus, but conversant with Plato, and his brother Dinostratus, rendered the whole of geometry as yet more perfect. But Theudius, the Magnian, appears[101] to have excelled, as well in mathematical disciplines, as in the rest of philosophy. For he constructed elements egregiously, and rendered many particulars more universal. Besides, Cyzicinus the Athenian, flourished at the same period, and became illustrious in other mathematical disciplines, but especially in geometry. These, therefore, resorted by turns to the Academy, and employed themselves in proposing common questions. But Hermotimus, the Colophonian, rendered more abundant what was formerly published by Eudoxus and Theætetus, and invented a multitude of elements, and wrote concerning some geometrical places. But Philippus the Mendæan[111], a disciple of Plato, and by him inflamed in the mathematical disciplines, both composed questions, according to the institutions of Plato, and proposed as the object of his enquiry whatever he thought conduced to the Platonic philosophy. And thus far historians produce the perfection of this science. But Euclid was not much junior to these, who collected elements, and constructed many of those things which were invented by Eudoxus; and perfected many which were discovered by Theætetus. Besides, he reduced to invincible demonstrations, such things as were exhibited by others with a weaker arm. But he lived in the times of the first Ptolemy: for Archimedes mentions Euclid, in his first book, and also in others. Besides, they relate that Euclid was asked by Ptolemy, whether there was any shorter way to the attainment of geometry than by his elementary institution, and that he answered, there was no other royal path which led to geometry. Euclid, therefore, was junior to the familiars of Plato, but more ancient than Eratosthenes and Archimedes (for these lived at one and the same time, according to the tradition of Eratosthenes) but he was of the Platonic sect, and familiar with its philosophy: and from hence he appointed the constitution of those figures which are called Platonic[112], as the end of his elementary institutions.
[102]
What Mathematical Volumes Euclid composed.
There are, therefore, many other mathematical volumes of this man, full of admirable diligence, and skilful consideration: for such are his Optics[113], and Catoptrics: and such also, are his elementary institutions, which conduce to the attainment of music[114]; and his book concerning divisions[115]. But his geometrical institution of the Elements is especially admirable, on account of the order and election of those theorems and problems, which are distributed through the Elements. For he does not assume all which might be said, but that only which could be delivered in an elementary order. Besides this, he exhibits modes of syllogisms of every kind; some, indeed, receiving credibility from causes, but others proceeding from certain signs; but all of them invincible and sure, and accommodated to science. But, besides these, he employs all the dialectic ways, dividing, indeed, in the inventions of forms; but defining in essential reasons: and again, demonstrating in the progressions from principles to things sought, but resolving in the reversions from things sought to principles. Besides this, we may view in his geometrical elements, the various species of conversions, as well of such as are simple as of such as are more composite. And again, what wholes may be converted with wholes: what wholes with parts; and on the other hand, what as parts with parts[116]. Besides this, we must say, that in the continuation of inventions, the dispositions and order of things preceding and following, and in the power with which he treats[103] every particular, he is not deceived, as if falling from science, and carried to its contrary, falsehood and ignorance. But because we may imagine many things as adhering to truth, and which are consequent to principles producing science, which nevertheless tend to that error which flows from the principles, and which deceives ruder minds, he has also delivered methods of the perspicacious prudence belonging to these. From the possession of which, we may exercise those in the invention of fallacies, who undertake this inspection, and may preserve ourselves from all deception. And this book, by which he procures us this preparation, is inscribed ψευδαρίος, or, concerning fallacies[117]. Because he enumerates in order their various modes, and in each exercises our cogitation with various theorems. And he compares truth with falsehood, and adapts the confutation of deception to experience itself. This book, therefore, contains a purgative and exercising power. But the institution of his elementary, skilful contemplation of geometrical concerns, possesses an invincible and perfect narration.
Concerning the Purport of Geometry.
But, perhaps, some one may enquire in what the design of this treatise consists? To this I answer, that its design is to be distinguished as well according to the objects of enquiry, as according to the learner. And, indeed, regarding the subject, we must affirm, that all the discourse of geometry is concerning the mundane figures. Because it begins from such things as are simple, but ends in the variety of their constitution. And, indeed, it constitutes each of them separately, but at the same time delivers their inscriptions in a sphere, and the proportions which they contain. On which account some have thought, that the design of each of the books is to be referred to the world; and they have delivered to our memory, the utility which they afford us in the contemplation of the universe.[104] But distinguishing the design with respect to the learner, we must affirm, that its purpose is the institution of elements; and the perfection of the learners cogitative powers in universal geometry. For beginning from these, we are enabled to understand the other parts of this science, and to comprehend the variety which they contain. And, indeed, without these, the discipline of the rest, is to us impossible and incomprehensible. For such theorems as are most principal and simple, and are most allied to first suppositions, are here collected in a becoming order. And the demonstrations of other mathematicians, use these as most known, and advance from these in their most complicated progressions. For thus Archimedes, in what he has writ concerning the sphere and cylinder, and Apollonius, and the rest of mathematicians, use, as evident principles, the things exhibited in this treatise. Its purpose, therefore, is the institution of learners in the whole geometric science, and to deliver the determinate constitutions of the mundane figures.
From whence the Name of Elementary Institution originated, and why Euclid is called the Institutor of Elements.
But what gave rise to the name of elementary institution, and of element itself, from which elementary institution was derived? To this we shall reply, by observing, that of theorems some are usually called elements, but others elementary, and others again are determined beyond the power of these. Hence, an element is that whose consideration passes to the science of other things, and from which we derive a solution of the doubts incident to the particular science we investigate. For as there are certain first principles of speech, most simple and indivisible, which we denominate elements, and from which all discourse is composed; so there are certain principal theorems of the whole of geometry, denominated elements, which have the respect of principles to the following theorems; which regard all the subsequent propositions, and afford the demonstrations of many accidents essential to the subjects of geometric speculation.[105] But things elementary are such as extend themselves to a multitude of propositions, and possess a certain simplicity and sweetness, yet are not of the same dignity with elements; because their contemplation is not common to all the science to which they belong, as is the case in the following theorem, that in triangles, perpendiculars, drawn from their angles to their sides, coincide in one point[118]. Lastly, whatever neither possesses a knowledge extended into multitude, nor exhibits any thing skilful and elegant, falls beyond the elementary power. Again, an element, as Menæchmus says, may have a twofold definition. For that which confirms, is an element of that which is confirmed; as the first proposition of Euclid with respect to the second, and the fourth with regard to the fifth. And thus, indeed, many things may be mutually called elements one of another; for they are mutually confirmed. Thus, because the external angles of right-lined figures, are equal to four right angles, the multitude of internal ones equal to right angles; and, on the contrary, that from this is exhibited[119]. Besides, an element is otherwise called that into which, because it is more simple, a composite is dissolved. But it must be observed, that every element cannot be called the element of every thing: but such as are more principal are the elements of such as are constituted in the reason of the thing effected; as petitions are the elements of theorems. And, according to this signification of an element, Euclid’s elements are constructed. Some, indeed, of that geometry which is conversant about planes; but others of stereometry. In the same manner, likewise, in arithmetic and astronomy, many have composed elementary institutions. But it is difficult, in each science, to chuse and conveniently ordain elements, from which all the peculiarities of that science originate, and into which they may be resolved. And among those who have undertaken this employment, some have been able to collect more, but others fewer elements. And some, indeed, have used shorter demonstrations; but others have extended their treatise to an infinite length. And some have omitted the method by an impossibility; but others[106] that by proportion; and others, again, have attempted preparations against arguments destroying principles. So that many methods of elementary institution have been invented by particular writers on this subject. But it is requisite that this treatise should entirely remove every thing superfluous, because it is an impediment to science. But every thing should be chosen, which contains and concludes the thing proposed; for this is most convenient and useful in science. The greatest care, likewise, should be paid to clearness and brevity; for the contraries to these, disturb our cogitation. Lastly, it should vindicate to itself, the universal comprehension of theorems, in their proper bounds: for such things as divide learning into particular fragments, produce an incomprehensible knowledge. But in all these modes, any one may easily find, that the elementary institution of Euclid excels the institutions of others. For its utility, indeed, especially confers to the contemplation of primary figures: but the transition from things more simple to such as are more various, and also that perception, which from axioms possesses the beginning of knowledge, produces clearness, and an orderly tradition: and the migration from first and principal theorems to the objects of enquiry, effects the universality of demonstration. For whatever he seems to omit, may either be known by the same ways, as the construction of a scalene and isosceles triangle[120]: or because they are difficult, and capable of infinite variety, they are far remote from the election of elements, such as the doctrine of perturbate proportions, which Apollonius has copiously handled: or, lastly, because they may be easily constructed from the things delivered, as from causes, such as many species of angles and lines. For these, indeed, were omitted by Euclid, and are largely discoursed of by others, and are known from simple propositions. And thus much concerning the universal elementary institution of geometry.
[107]
Concerning the Order of Geometrical Discourses.
But let us now explain the universal order of the discourses contained in geometry. Because then, we assert that this science consists from hypothesis[121], and demonstrates its consequent propositions from definite principles (for one science only, I mean the first philosophy, is without supposition, but all the rest assume their principles from this) it is necessary that he who constructs the geometrical institution of elements, should separately deliver the principles of the science, and separately the conclusions which flow from those principles; and that he should render no reason concerning the nature or truth of the principles, but should confirm by reasons, the things consequent to these geometric principles. For no science demonstrates its own principles, nor discourses concerning them; but procures to itself a belief of their reality, and they become more evident to the particular science to which they belong than the things derived from them as their source. And these, indeed, science knows by themselves; but their consequents, through the medium of these. For thus, also, the natural philosopher propagates his reasons from a definite principle, supposing the existence of motion. Thus too, the physician, and he who is skilled in any of the other sciences and arts. For if any one mingles principles, and things flowing from principles into one and the same, he disturbs the whole order of knowledge, and conglutinates things which can never mutually agree; since a principle, and its emanating consequent, are naturally distinct from each other. In the first place, therefore (as I have said), principles in the geometric institution are to be distinguished from their consequents, which is performed by Euclid in each of his books; who, before every treatise, exhibits the common principles of this science; and afterwards divides these common principles into hypotheses, petitions, and axioms. For all these mutually differ; nor is an axiom, petition,[108] and hypothesis the same, according to the demoniacal Aristotle; but when that which is assumed in the order of a principle, is indeed known to the learner, and credible by itself, it is an axiom: such as, that things equal to the same, are mutually equal to each other. But when any one, hearing another speak concerning that of which he has no self-evident knowledge, gives this assent to its assumption, this is hypothesis. For that a circle is a figure of such a particular kind, we presume (not according to any common conception) without any preceding doctrine. But when, again, that which is asserted was neither known, nor admitted by the learner, yet is assumed, then (says he) we call it petition; as the assumption that all right angles are equal. But the truth of this is evinced by those who study to treat of some petition, as of that which cannot by itself be admitted by any one. And thus, according to the doctrine of Aristotle[122], are axiom, petition, and supposition distinguished. But oftentimes, some denominate all these hypotheses, in the same manner as the Stoics call every simple enunciation an axiom. So that, according to their opinion, hypotheses also will be axioms; but, according to the opinion of others, axioms will be called suppositions. Again, such things as flow from principles are divided into problems and theorems. The first, indeed, containing the origin, sections, ablations, or additions of figures, and all the affections with which they are conversant; but the other exhibiting the accidents essential to each figure. For, as things effective of science, participate of contemplation, in the same manner things contemplative previously assume problems in the place of operations. But formerly some of the ancient mathematicians thought that all geometrical propositions should be called theorems, as the followers of Speusippus and Amphinomus, believing, that to contemplative sciences, the appellation of theorems is more proper than that of problems; especially since they discourse concerning eternal and immutable objects. For origin does not subsist among things eternal: on which account, problems cannot have any place in these sciences; since they enunciate origin, and the production of that which formerly had no existence, as the construction of an equilateral[109] triangle, or the description of a square on a given right line, or the position of a right line at a given point. It is better, therefore (say they), to assert that all propositions are of the speculative kind; but that we perceive their origin, not by production, but by knowledge, receiving things eternal as if they were generated; and on this account we ought to conceive all those theorematically, but not problematically. But others, on the contrary, think that all should be called problems; as those mathematicians who have followed Menæchmus. But that the office of problems is twofold, sometimes, indeed, to procure the thing sought; but at other times when they have received the determinate object of enquiry, to see, either what it is, or of what kind it is, or what affection it possesses, or what its relation is to another. And, indeed, the assertions of each are right; for the followers of Speusippus well perceive. Since the problems of geometry are not of the same kind, with such as are mechanical. For these are sensibles, and are endued with origin, and mutation of every kind. And, on the other hand, those who follow Menæchmus do not dissent from truth: since the inventions of theorems cannot by any means take place without an approach into matter; I mean intelligible matter. Reasons, therefore, proceeding into this, and giving form to its formless nature, are not undeservedly said to be assimilated to generations. For we say that the motion of our cogitation, and the production of its inherent reasons, is the origin of the figures situated in the phantasy, and of the affections with which they are conversant: for there constructions and sections, positions and applications, additions and ablations, exist: but every thing resident in cogitation, subsists without origin and mutation. There are, therefore, both geometrical problems and theorems. But, because contemplation abounds in geometry, as production in mechanics, all problems participate of contemplation; but every thing contemplative is not problematical. For demonstrations are entirely the work of contemplation; but every thing in geometry posterior to the principles, is assumed by demonstration. Hence, a theorem is more common: but all theorems do not require problems; for there are some which possess from themselves the demonstration of the thing sought. But others, distinguishing a theorem from a problem, say,[110] that indeed every problem receives whatever is predicated of its matter, together with its own opposite: but that every theorem receives, indeed, its symptom predicate, but not its opposite. But I call the matter of these, that genus which is the subject of enquiry; as for instance, a triangle, quadrangle, or a circle: but the symptom predicate, that which is denominated an essential accident, as equality, or section, or position, or some other affection of this kind. When, therefore, any one proposes to inscribe an equilateral triangle in a circle, he proposes a problem: for it is possible to inscribe one that is not equilateral. But when any one asserts that the angles at the base of an isosceles triangle are equal, we must affirm that he proposes a theorem; for it is not possible that the angles at the base of an isosceles triangle should be unequal to each other. On which account, if any one forming problematically, should say that he wishes to inscribe a right angle in a semi-circle, he must be considered as ignorant of geometry; since every angle in a semi-circle is necessarily a right one. Hence, propositions which have an universal symptom, attending the whole matter, must be called theorems; but those in which the symptom is not universal, and does not attend its subject, must be considered as problems. As to bisect a given terminated right line, or to cut it into equal parts: for it is possible to cut it into unequal parts. To bisect every rectilinear angle, or divide it into equal parts; for a division may be given into unequal parts. On a given right line to describe a quadrangle; for a figure that is not quadrangular may be described. And, in short, all of this kind belong to the problematical order. But the followers of Zenodotus, who was familiar with the doctrine of Oenopides, but the disciple of Andron, distinguish a theorem from a problem, so far as a theorem enquires what the symptom is which is predicated of the matter it contains; but a problem enquires what that is, the existence of which is granted. From whence the followers of Possidonius define a theorem a proposition, by which it is enquired whether a thing exists or not; but a problem, a proposition, in which it is enquired what a thing is, or the manner of its existence. And they say that we ought to form the contemplating proposition by enunciating, as that every triangle has two sides greater than the remaining one, and that[111] the angles at the base of every isosceles triangle are equal: but we must form the problematical proposition, as if enquiring whether a triangle is to be constructed upon this right line. For there is a difference, say they, absolutely and indefinitely, to enquire whether the thing proposed is from a given point to erect a right line at right angles to a given line, and to behold what the perpendicular is. And thus, from what has been said, it is manifest there is some difference between a problem and a theorem. But that the elementary institution of Euclid, also, consists partly of problems, and partly of theorems, will be manifest from considering the several propositions. Since, in the conclusion of his demonstrations, he sometimes adds (which was to be shewn) sometimes (which was to be done) the latter sentence being the mark or symbol of problems, and the former of theorems. For although, as we have said, demonstration takes place in problems, yet it is often for the sake of generation; for we assume demonstration in order to shew, that what was commanded is accomplished: but sometimes it is worthy by itself, since the nature of the thing sought after may be brought into the midst. But you will find Euclid sometimes combining theorems with problems, and using them alternately, as in the first book; but sometimes abounding with the one and not the other. For the fourth book is wholly problematical; but the fifth is entirely composed from theorems. And thus much concerning the order of geometrical propositions.
Concerning the Design of the first Book,—its Division,—and a previous Admonition to the Reader.
But, after these considerations, when we have determined the design of the first book, and have exhibited its division, we shall enter upon the treatise of the definitions. The design, then, of this book, is to deliver the principles of the contemplation of right lines. For though a circle, and its consideration, is more excellent than the essence and knowledge of right lines, yet the doctrine concerning these is more adapted to us, who are hastening to transfer our cogitation[112] from more imperfect and sensible natures, to such as are intelligible. For, indeed, right lined figures are proper to sensibles, but a circle to intelligibles. Because that which is simple, uniform, and definite, is proper to the nature of the things which are: but that which is various, and which increases indefinitely from the number of its containing sides, regards the fluctuating essence of sensible particulars. Hence, in this book, the first and most principal of right lined figures are delivered; I mean the triangle and parallelogram. For in these, as under their proper genus, the causes of the elements are contained: viz. the isosceles and scalene, and those which are formed from these, the equilateral triangle, and the quadrangle, from which the four figures of the elements are composed. We shall find, therefore, as well the origin of the equilateral triangle as of the quadrangle; of the last, indeed, upon, but of the first from a given right line. [[123]An equilateral triangle, therefore, is the proximate cause of the three elements, fire, air, and water: but a quadrangle is annexed to earth.] And lastly, the design of the first book is adapted to the whole treatise, and confers to the universal knowledge of the mundane elements. Besides, it instructs learners in the science concerning right-lined figures; since it rightly invents, and accurately collects, the first principles of these.
But this book is divided into three greatest parts, of which the first declares the origin and properties of triangles, as well according to angles, as also according to sides. Besides, it makes mutual comparisons of these, and beholds every one by itself. For receiving one triangle, sometimes it considers the angles from the sides; but sometimes the sides from the angles: and this according to equality and inequality. And supposing two triangles, it discovers the same property again, by various methods. But the second part combines the contemplation of parallelograms, describing their properties and generations. And the third part shews the communication of triangles[113] and parallelograms, both in symptoms and mutual comparisons. For it shews that triangles and parallelograms constituted on the same and on equal bases, are affected with the same passions; and by complication, when both stand upon one base: and again, after what manner a parallelogram may be made equal to a triangle; and lastly, concerning the proportion which in right angled triangles, the square made from the side subtending, has to the squares containing the right angle. And such is the division of the first Book.
But, previous to our enquiry into each of these parts, we think it requisite to admonish the reader, that he must not require of us, those small assumptions, and cases, and whatever else there may be of that kind, which has been divulged by our predecessors. For we are satiated with these, and shall, therefore, but rarely adopt them in our discourse. But whatever has a more difficult contemplation, and regards universal philosophy, of this we shall make a particular relation: imitating the Pythagoreans, with whom this ænigma was common, “a[124] figure and a step: but not a figure and three oboli,” shewing by this, that it is requisite to pursue that philosophy which ascends every theorem by a step, and raises the soul on high; but does not suffer it to remain among sensibles, to fill up the use attendant on mortals, and, consulting for this, to neglect the elevation which rises from hence to an intelligible essence.
[114]
DEFINITIONS.
A Point is that which has no Parts.
That geometry, according to the transition which takes place from things more composite to such as are more simple, runs from body, which is diffused into distance by three dimensions, to a superficies by which it is bounded; but from superficies to a line, the boundary of superficies; and from a line to a point destitute of all dimension, has been often said, and is perfectly manifest. But because these terms, in many places, on account of their simplicity, appear to be more excellent than the nature of composites; but in many, as when they subsist in things which they terminate, they are similar to accidents, it is necessary to determine in what genera of beings each of these may be beheld[125]. I say then, that such things as are destitute of matter, which subsist in separate reasons, and in those forms which are placed under themselves, are always allotted a subsistence of more simple essences, superior to the subsistence of such as are more composite. On this account, both in intellect, and in the ornaments, as well of the middle kind as among those peculiar to the soul, and in natures themselves, the terms which proximately vivify bodies, excel according to essence the things which are terminated; and are more impartible, more uniform, and more primary than these. For in immaterial forms, unity is more perfect than multitude; that which[115] is impartible, than that which is endued with unbounded progression; and that which terminates, than that which receives bound from another. But such things as are indigent of matter, and abide in others, and degenerate from the perfection of their essence, which are scattered about subjects, and have an unnatural union, are allotted more composite reasons, prior to such as are more simple. Hence, things which appear in the phantasy invested with form, and the matter of the figures which the phantasy contains, and whatever in sensibles is generated by nature, have, in a preceding order, the reasons of the things terminated; but the reasons which terminate, in a following and adventitious rank[126].] For lest that which is distributed into three dimensions, should be extended into infinite magnitude, either according to intelligence or sense, it was every way terminated by superficies. And lest a plane superficies should conceal itself in an infinite progression, a line approaching opposed its diffusion, and gave bound to its indefinite extension. And, in like manner, a point limited the progressions of a line; composite natures deriving their subsistence from such as are simple. For this also is again manifest, that in separate forms the reasons of terms subsist in themselves, but not in those which are terminated; and abiding such as they are in reality, possess a power of constituting secondary natures. But, in inseparable forms they give themselves up to things which are terminated, reside in them, become, as it were, their parts, and are replenished with baser natures. On which account, that which is impartible is there endued with a partible essence, and that which is void of latitude is diffused into breadth. And terms are no longer able to preserve their simplicity and purity. For since they abide in another, they necessarily change their own nature into the matter of their containing subject. Matter, indeed, disturbs the perfection of these, and causes the reason of a plane to become a profound plane; but obscuring the one dimension of a line, causes it to be every way partible; and gives corporeity to the indivisibility of a point, and separates it together with the natures which it terminates. For all these reasons falling into matter, the one kind from cogitation into intelligible[116] matter, but the other from nature into that which is sensible, are replenished with their containing subjects; and depart from their own simplicity, into foreign compositions and intervals. But here a doubt arises how all these, existing in intellect and soul in an impartible manner, and without any dimension, are distributed into matter, some indeed, principally, but others on account of its nature? Shall we say that there is a certain order in immaterial forms, so that some are allotted the first, some the middle, and others the last place; and that of forms some are more uniform, but that others are more multiplied; and that some have their powers collected together, but others tending into interval; and that some, again, border upon bound, but that others are proximate to infinity? For though all participate of these two principles, yet some originate from bound, but others from infinity, of which they more largely participate. Hence, a point is entirely impartible, since it subsists according to bound, yet it occultly contains an infinite power, by which it produces every interval, and the progression of all intervals, unfolds its infinite power. But body, and the reason of body, participates more of an infinite nature; on which account it is among the number of things terminated by another, and divisible in infinitum, according to all dimensions. But the mediums between these, according to the distance of the extremes, are either among the number of things which have an abundance of bound; or among such as have an affluence of infinity: on which account they both terminate and are terminated. For, indeed, so far as they consist from bound, they are able to terminate others; but so far as they participate of infinity, they are indigent of termination from others, Hence, since a point is also a bound, it preserves its proper power in participation: but since it likewise contains infinity occultly, and is compelled to be every where present with the natures which it terminates, it resides with them infinitely. And, because among immaterial forms there was a certain infinite power capable of producing things distant from each other by intervals, a point is present with its participants in capacity. For infinity in intelligibles is the primary cause and prolific power of the universe; but in material natures it is imperfect, and is alone all things in dormant capacity. And in short, those forms which, on account of their[117] simplicity and impartibility, hold a superior rank among principles, preserve, indeed, (in conformity to their nature,) their own property in their participations, but become worse than more composite reasons. For matter is able to participate these more clearly, and to be prepared for their reception, rather than that of the most simple causes of beings. On which account, the vestigies of separate principles descend into matter; but the participations of those in a second and third order, become more conspicuous. Hence, matter participates more of the cause of body, than of a plane; and of this more than the form of a line; and of this still more than that of a point, which contains all these, and is the boundary of them all. For the reason of a point presides over this whole series, unites and contains all partible natures, terminates their progressions, produces them all by its infinite power, and comprehends them in its indivisible bound. On which account also, in the images of immaterial forms, some are the boundaries of others; but a point is the limit of them all. But that we must not think with the Stoics, that these boundaries of bodies alone subsist from cogitation; but that there are certain natures of this kind among beings, which previously contain the demiurgical reasons of things, we shall be enabled to remember, if we regard the whole world, the convolutions of its parts, the centres of those convolutions, and the axes which penetrate through the whole of these revolving circles. For the centres subsist in energy, since they contain the spheres, preserve them in their proper state, unite their intervals, and bind and establish to themselves the powers which they possess. But the axes themselves being in an immoveable position, evolve the spheres, give them a circular motion, and a revolution round their own abiding nature. And the poles of the spheres, which both terminate the axes, and bind in themselves the other convolutions, do they not perspicuously evince, that points are endued with demiurgical and capacious powers, that they are perfective of every thing distant by intervals, and are the sources of union, and an unceasing motion? From whence, indeed, Plato[127] also says, that they have an adamantine subsistence; shewing by this, the immutable, eternal, and stable power[118] of their essence, ever preserving itself in the same uniform mode of existence. He adds too, that the whole spindle of the Fates, is turned about these, and leaps round their coercive union. But other more recondite and abstruse discourses affirm, that the demiurgus presides over the world, seated in the poles, and, by his divine love, converting the universe to himself. But the Pythagoreans thought that the pole should be called the Seal of Rhea[128]; because the zoogonic, or vivific goddess, pours through these into the universe, an inexplicable and efficacious power. And the centre they called the prison of Jupiter; because, since Jupiter has placed a demiurgical guard in the bosom of the world, he has firmly established it in the midst. For, indeed, the centre abiding, the universe possesses its immoveable ornament, and unceasing convolution: and the gods who preside over the poles, obtain a power collective of divisible natures, and unific of such as are multiplied: and those who are allotted the government of the axes, restrain and eternally evolve their perpetual convolutions. And, if it is lawful to offer our own opinion on this subject, the centres and poles of all the spheres are the symbols of the conciliating gods, shadowing forth their imperceptible and unifying composition. But the axes express the coherencies of the universal ornaments; and are endued with a power of comprehending the mundane integrities and periods, in the same manner as their presiding deities, of such as are intellectual. But the spheres themselves are images of the gods, called perfectors of works, copulating the principle with the end, and excelling all figures in simplicity, similitude, and perfection. But we have been thus prolix, that we might evince the power of impartibles, and of the terms which the world contains, and that so far as they bear an image of primary and most principal causes, they are allotted the most excellent order in the universe. For centres and poles are not of the same kind with things which are terminated; but they subsist in energy, and possess an essence, and perfect power, which pervades through all partible natures. But many beholding those terms which imperfectly subsist in terminated essences, consider them as endued with a slender subsistence; and some indeed say, that[119] they are alone separated from sensibles by thought; but others, that they have an essence no where but in our thoughts. However, since the forms of all these are found both in the nature of intellect, in the ornaments of soul, in the nature of things, and in inferior bodies, let us consider how, according to the order they contain, they subsist in the genera of beings. And indeed, all of them pre-exist in intellect, but in an impartible and uniform manner: so that they all subsist according to one form, the reason of a point, which exists occultly and impartibly. But they all subsist in soul according to the form of a line: on which account Timæus also composes the soul from right and circular lines: for every circle is a line alone[129]. But they all subsist in natures, according to the reason of a plane; and on this account, Plato commands us to manifest those natural reasons, which are endued with a power of constituting bodies by a plane. And the resolution of bodies into planes leads us to the proximate cause of appearances. Lastly, they all subsist in bodies, but in a corporeal manner; since all forms have their being in these, according to the partible nature of bodies. Hence, all of them appear every where, and each according to its proper order; and diversity arises from pre-dominating power. The point, indeed, is every where impartible, and when that which is divisible into parts, excels according to the diminution of beings, it vindicates to itself, an illustrious subsistence of partible natures. And sometimes the point is entirely superior, according to the excellence of cause; but sometimes it is connected with divisibles, and sometimes it is allotted in them an adventitious existence; and, as if swallowed up by the partition of the lowest natures, loses its own proper impartibility. As, therefore, with respect to the monad, one[130] is the mother of number, but the other is as[120] matter spread under, and the receptacle of numbers; and each of them a principle, (yet neither of them is number), but in a different respect: in the same manner a point also, is partly the parent and author of magnitudes; but is partly a principle in another respect, and not according to a generative cause. But is a point, then, the only impartible? Or may we affirm this of the now in time, and of unity in numbers? Shall we not say, that to the philosopher, indeed, discoursing concerning the universality of things, it is proper to behold every thing, however falling under distribution; but that to him who is endued with the science of particulars, who produces his contemplation from certain definite principles, and runs back even to these, but very little scrutinizes the progressions of beings, it is requisite to attempt, consider, and treat concerning that impartible nature alone, which regards his first principles; and to behold that simplicity which presides over all the particular subjects of his knowledge? In consequence of this reasoning, therefore, a point alone, according to the geometric matter, is destitute of partition; but unity according to that which is arithmetical. And the reason of a point, however in some other respects it may be imperfect, yet is perfect in the present science. For, indeed, the physician also says, that the elements of bodies are fire and water, and things similar to these; and as far as to these the resolution of bodies proceeds. But the natural philosopher passes on to more simple elements; and the one defines an element simple as to sense, but the other simple as to reason; and both of them properly as to their peculiar science. We must not, therefore, think that the definition of a point is faulty, nor determine it as imperfect; for so far as pertains to the geometric matter, and its principles, it is sufficiently delivered. This alone, indeed, is wanting to its completion, that the definition does not clearly say, that which is impartible with me is a point; and my principle, and that which I contain as most simple, is nothing else than this. And after this manner it is proper to hear the geometrician addressing us. Euclid, therefore, from a negation of parts, declares to us a principle, leading to the theory of its whole subject nature. For negative discourses are proper to principles, as Parmenides teaches us, who delivers the doctrine concerning the first and last cause, by negations alone. Since every principle consists of[121] an essence different from its flowing consequents; and the negations of these exhibit to us the property of their source. For that it is, indeed, the cause of these, yet at the same time has nothing in common with these, becomes perspicuous from a doctrine of this kind. But here a doubt may arise, how, since the phantasy receives all things invested with forms, and in a partible manner, the geometrician beholds in it the point destitute of parts? For it is not because they are reasons existing in cogitation, but the phantasy receives the resemblances of intellectual and divine forms according to its own proper nature, exhibiting in its shadowy bosom the forms of formless natures, and clothing with figure things entirely free from the affections of figure. To this ambiguity we must say, that the species of imaginative motion is neither alone partible, nor impartible; but that it proceeds from the impartible to the partible, and from the formless nature to that which is expressed by form. For if it was partible alone, it could not preserve in itself many impressions of forms, since the subsequent would obscure the pre-existent figures: for no body can contain at once, and according to the same situation, a multitude of figures; but the former will be blotted out by the succession of the latter. But if it was alone impartible, it would not be inferior to cogitation, and to soul, which surveys all things in an impartible manner. Hence, it is necessary that it should indeed begin from an impartible according to its motion, and from thence draw forth the folded and scattered form of every thing falling under cogitation, and penetrating to its shadowy receptacle: but, that it should at length end in form, figure, and interval. And if it be allotted a nature of this kind, it will, after a certain manner, contain an impartible essence: and a point, according to this, must be said to have its principal subsistence: for the form of a line is contracted in the phantasy according to this. Hence, because it possesses a twofold power, impartible and partible, it will indeed contain a point in an impartible, and intervals in a partible manner. But as the Pythagoreans define a point to be unity having position, let us consider what they mean. That numbers, indeed, are more immaterial and more pure than magnitudes, and that the principle of numbers is more simple than the principle of magnitudes, is manifest to every one: but when they say that a[122] point is unity endued with position, they appear to me to evince that unity and number subsist in opinion: I mean monadic number[131]. On which account, every number, as the pentad and the heptad, is one in every soul, and not many; and they are destitute of figure and adventitious form. But a point openly presents itself in the phantasy, subsists, as it were, in place, and is material according to intelligible matter. Unity, therefore, has no position, so far as it is immaterial, and free from all interval and place: but a point has position, so far as it appears seated in the bosom of the phantasy, and has a material subsistence. But unity is still more simple than a point, on account of the community of principles. Since a point exceeds unity according to position; but appositions in incorporeals produce diminutions of those natures, by which the appositions are received.
A Line is a Length without Breadth.
A Line obtains the second place in the Definitions, as it is by far the first and most simple interval, which the geometrician calls a length, adding also without breadth; since a line, in respect of a superficies, ranks as a principle. For he defines a point, as it is the principle of all magnitudes, by negation alone; but a line, as well by affirmation as by negation. Hence it is a length, and by this exceeds the impartibility of a point; but it is without breadth, because it is separated from other dimensions. For, indeed, every thing which is void of breadth, is also destitute of bulk, but the contrary is not true, that every thing void of bulk is also destitute of breadth. Since, therefore, he has removed breadth from a line, he has also removed at the same time bulk. On which account he does not add, that a line also has no thickness, because this property is consequent to the notion of being without breadth. But it is defined by others in various ways: for some call it the flux of a point, but others a magnitude contained by one interval. And this definition,[123] indeed; is perfect, and sufficiently explains the essence of a line; but that which calls it the flux of a point, appears to manifest its nature from its producing cause; and does not express every line, but alone that which is immaterial. For this is produced by a point, which though impartible itself, is the cause of being to partible natures. But the flux of a point, shews its progression and prolific power, approaching to every interval, receiving no detriment, perpetually abiding the same, and affording essence to all partible magnitudes. However, these observations are known, and manifest to every one. But we shall recall into our memory, discourses more Pythagorical, which determine a point as analogous to unity, a line to the duad, a superficies to the triad, and body to the tetrad. [[132]Yet when we compare those which receive interval together, we shall find a line monadic; but a superficies dyadic, and a solid body triadic.] From whence also, Aristotle[133] says; that body is perfected by the ternary number. And, indeed, this is not wonderful, that a point, on account of its impartibility, should be assimilated to unity; but that things subsequent to a point, should subsist according to numbers proceeding from unity, and should preserve the same proportion to a point, as numbers to unity; and that every one should participate of its proximate superior, and have the same proportion to its kindred, and following degree, as the superior to this, which is the immediate consequent. [[134]For example, that a line has the order of the duad with respect to the point, but of unity to a superficies; and that this last has the relation of a triad to the point, but of the duad to a solid.] And on this account, body is tetradic, with respect to a point, but triadic as to a line. Each order, therefore, has its proportion; but the order of the Pythagoreans is the more principal, which receives its commencement from an exalted source, and follows the nature of beings. For a point is indeed twofold; since it either subsists by itself, or in a line; in which last respect also, since as a boundary it is alone and one, neither having a whole nor parts, it imitates the supreme[124] nature of beings. On which account too, it was placed in a correspondent proportion to unity. [135]For as the oracle says, Unity is there first, where the paternal unity abides. But a line is the first endued with parts and a whole, and it is monadic because it is distant by one interval only; and dyadic on account of its progression: for if it be infinite, it participates of the indefinite duad; but if finite, it requires two terms, from whence and to what place; since, on account of these it imitates totality, and is allotted an order among totals. For unity, according to the oracle, is extended[136], and generates two; and this produces a progression into longitude, together with that which is distant extendedly, and with one interval, and the matter of the duad. But superficies, since it is both a triad and duad, as also the receptacle of the primary figures, and that which receives the first form and species, is in a certain respect similar to the triadic nature, which first terminates beings; and to the duad, by which they are divided and dispersed. But a solid, since it has a triple distance, and is distinguished by the tetrad, which is endued with a power of comprehending all reasons, is reduced to that order in which the distinction of corporeal ornaments appears; as also the division of the universe into three parts, together with the tetradic property, which is generative and female. And these observations, indeed, might be more largely discussed, but for the present, must be omitted. Again, the discourse of the Pythagoreans, not undeservedly, calls a line, which is the second in order, and is constituted according to the first motion from an impartible nature, dyadic. And that a point is posterior to unity, a line to the duad, and a superficies to the triad, Parmenides himself shews, by first of all taking away multitude from one by negation, and afterwards the whole. Because, if multitude is before that which is a whole, number also will be prior to that which is continuous, and the duad to the line, and unity to the point: since the epithet not many, belongs to unity which generates multitude, but[125] to the point, the term not a whole, is proper, because it produces a whole; for this is said to have no part. And these things are affirmed of a line, while we more accurately contemplate its nature. But we should also admit the followers of Apollonius, who say, that we obtain a notion of a line, when we are ordered to measure the lengths alone, either of ways or walls; for we do not then subjoin either breadth or bulk, but only make one distance the object of our consideration. In the same manner we perceive superficies, when we measure fields; and a solid, when we take the dimensions of wells. For then, collecting all the distances together, we say, that the space of the well is so much, according to length, breadth, and depth. But a line may become the object of our sensation, if we behold the divisions of lucid places from those which are dark, and survey the moon when dichotomized: for this medium has no distance with respect to latitude; but is endued with longitude, which is extended together with the light and shadow.
But the Extremities of a Line are Points.
Every composite receives its bound from that which is simple, and every thing partible from that which is impartible; and the images of these openly present themselves in mathematical principles. For when it is said that a line is terminated by points, it seems manifestly to make it of itself infinite, because, on account of its proper progression, it has no extremity. As, therefore, the duad is terminated by unity, and reduces its own intolerable boldness under bound, when it is restrained in its comprehensive embrace: so a line also is limited by the points which it contains. For, since it is similar to the duad, it participates of a point having the relation of unity, according to the nature of the duad. Indeed, in imaginative, as well as in sensible forms, the points themselves terminate the lines in which they reside. But in immaterial forms, the reason of the impartible point pre-exists separate and apart; but when proceeding from thence by far the first of all, by determining itself with interval, moving itself, and flowing[126] in infinite progression, and imitating the indefinite duad, it is restrained indeed, by its proper principle, is united by its power, and on every side seized by its coercive bound. Hence it is, at the same time, both infinite and finite: infinite, indeed, according to its progression; but finite according to its participation of a terminating cause. So that, when it approaches to this cause, it is detained in its comprehension, and is terminated according to its union. Hence too, in the images of incorporeal forms, a point is said to terminate a line, by occupying its beginning and end. Bound, therefore, in immaterials, is separated from that which is bounded: but here it is twofold; for it subsists in that which is terminated. And this affords a wonderful symptom, that forms; indeed, abiding in themselves, precede their participants according to cause; but when giving themselves up to their subordinate natures, subsist according to their diversified properties: since they are multiplied and distributed together with these, and receive the division of their subjects. Besides, this also must be previously received concerning a line, that our geometrician uses it in a threefold acceptation. As terminated on both sides, and finite; as in the problem[137] which says, Upon a given terminated right line to construct an equilateral triangle. And as partly infinite and partly finite; as in the problem which commands us from three right lines, which are equal to three given right lines, to construct a triangle; for in the construction of the problem, he says, Let there be placed a certain right line, on one part finite, but on the other part infinite. And again, a line is received by Euclid as on both sides infinite; as in the problem which says, Upon a given infinite right line, from a given point, which is not in that line, to let fall a perpendicular. But, besides this, the following doubts, since they are worthy of solution, must[127] not be omitted. How are points called the extremities of a line? and of what line, since they can neither be the bounds of one that is infinite, nor of every finite? For there is a certain line, which is both finite, and has not points for its extremities. And such is a circular line, which returns into itself, and is not bounded by points, like a right line. And such also is the ellipsis, or line like a shield. Is it therefore requisite to behold a line, considered as a line? for we must receive a certain circumference, which is terminated by points, and a part of the elliptic line; having, in like manner, its extremities bounded by points. But every circular and elliptic line, assumes to itself another certain property, by which it is not line alone, but is also endued with a power of perfecting figure[138]. Lines, themselves, therefore, have their extremities terminated by points; but those which are effective of such like figures, return into themselves. And, indeed, if you conceive them to be described, you will also find how they are bounded by points; but if you receive them already described, and connect the end with the beginning, you can no longer behold their extremes.
A Right Line, is that which is equally situated between its bounding Points.
Plato establishing two most simple and principal species of lines, the right and the circular, composes all the rest from the mixture of these; I mean such as are called curve lines, some of which are formed from planes; but others subsist about solids; and whatever species of curve lines are produced by the sections of solids. And it seems, indeed, that a point (if it be lawful so to speak) bears an image of the one itself, according to Plato: for unity has no part, as he also shews in the Parmenides. But, because after unity itself there are three hypostases, or substances, bound, infinite, and that which is[128] mixed from these, the species of lines, angles, and figures, which subsist in the nature of things originate from thence. And, indeed, a circumference and a circular angle, and a circle among plane figures, and a sphere among solids, are analogous to bound. But a right line corresponds to infinity, according to all these; for it properly belongs to all, if it is beheld as existing in each. But that which is mixed in all these, is analogous to the mixt which subsists among intelligibles. For lines are mixed, as those which are called spirals. And angles, as the semi-circular and cornicular[139]. And plane figures, as segments and apsides; but solids, as cones and cylinders, and others of that kind. Bound, therefore, infinite, and that which is mixed,[129] are participated by all these. But Aristotle[140] likewise assents to Plato; for every species of lines, says he, is either right or circular, or mixed from these two. From whence also there are three motions, one according to a right line; the other circular; and the third mixed. But some oppose this division, and say that there are not two simple lines alone, but that there is a certain third line given, i. e. a helix or spiral, which is described about a cylinder[141], when, whilst a right line is moved round the superficies of the cylinder, a point in the line is carried along with an equal celerity. For by this means, a helix, or circumvolute line, is produced, which adapts all the parts of itself to all, according to a similitude of parts, as Apollonius shews in his book concerning the Cochlea; which passion, among all spirals, agrees to this alone. For the parts of a plane helix are dissimilar among themselves; as also of those which are described about a cone and sphere. But the cylindric spiral alone, consists of similar parts in the same manner as a right and circular line. Are there, then, three simple lines, and not two only? To which doubt we reply, that a helix of this kind is, indeed, of similar parts, as Apollonius teaches, but is by no means simple; since among natural productions, gold and silver are composed of similar parts, but are not simple bodies. But the generation of the cylindric helix evinces that its mixture is from things simple; for it originates while a right line is circularly moved round the axis of the cylinder, a point at the same time flowing along in the right line. Two simple motions, therefore, compose its nature; and, on this account, it is among the number of mixt lines, and not among such as are simple: for that which is composed from dissimilars is not simple, but mixt. Hence, Geminus, with great propriety, when he admits that some simple lines may be produced from many motions, does not grant that every such line is mixt; but that alone, which arises from dissimilar motions. For if you conceive[130] a square, and two motions which are performed with an equal celerity, one according to the length, but the other according to the breadth, a right line or the diameter will be produced; but the right line will not, on this account, be mixed: for no other line precedes it, formed by a simple motion, as we asserted of the cylindric helix. Nor yet, if you suppose a right line, moving in a right angle, and by a bisection to describe a circle[142], is the circular line, on this account, produced with mixture: for the extremities of that which is moved after this manner, since they are equally moved, will describe a right line; and the bisection, since it is unequally devolved, will delineate a circle; but the other points will describe an ellipsis. On which account, the[131] generation of a circular line is the consequence of that inequality of lation arising from the bisection; because a right line was supposed to be moved in a right angle, but not in a natural manner. And thus much concerning the generation of lines. But it seems, that of the two simple lines, the right and the circular, the right line is the more simple; for in this, dissimilitude cannot be conceived, even in opinion. But in the circular line, the concave and the convex, indicate dissimilitude. And a right line, indeed, does not infer a circumference according to thought; but a circumference brings with it a right line, though not according to its generation, yet with respect to its centre. But what if it should be said that a circumference requires a right line to its construction! For if either extreme of a right line remains fixt, but the other is moved, it will doubtless describe a circle, whose centre will be the abiding extreme of the right line. Shall we say that the generator of the circle is the point which is carried about the abiding point, but not the right line itself? For the line only determines the distance, but the point composes the circular line, while it is moved in a circular manner: but of this enough. Again, a circumference appears to be proximate to bound, and to have the same proportion to other lines, as bound to the universality of things. For it is finite, and is alone among simple lines perfective of figure. But a right line is proximate to infinity; for its capacity of infinite extension never fails: and as all the rest are produced from bound and infinite, in the same manner from the circular and right line, every mixt genus of lines is composed, as well of planes as of those which consist in solid bodies. And on this account, the soul also[143] previously assumed into herself the right and circular according to her essence, that she might moderate all the co-ordination of infinite, and all the nature of bound, which the world contains. By a right line, indeed, constituting the progression of these principles into the universe; but by a circular line, their return to their original source: and by the one, producing all things into multitude; but by the other, collecting them into one. And not only the soul, but he also who produced the soul, and endued her with these powers, contains in himself both these primary causes.[132] For when he previously assumed the beginning, middle, and end of all things, he terminated right lines (says Plato[144]), by a circular progression according to nature. And proceeding to all things by provident energies, and returning to himself, he established himself, says Timæus, after his own peculiar manner. But a right line is the mark or symbol of a providence, indeclinable, incapable of perversion, immaculate, never-failing, omnipotent, and present to all beings, and to every part of the universe. But a circumference, and that which environs, is the symbol of an energy retiring into union with itself, and which rules over all things according to one intellectual bound. When, therefore, the demiurgus of the universe had established in himself these two principles, the right and the circular line, and had given them dominion, he produced from himself two unities; the one, indeed, energizing according to the circular line, and being effective of intellectual essences; but the other according to the right line, and affording an origin to sensible natures. But because the soul is allotted a middle situation between intellectuals and sensibles, so far, indeed, as she adheres to an intellectual nature, she energizes according to the circle; but so far as she presides over sensibles, she provides for their welfare according to the right line: and thus much concerning the similitude of these forms to the universality of things. But Euclid, indeed, has properly delivered the present definition of a line; by which he shews that a right line alone occupies a space equal to that which is situated between its points: for as much as is the distance of one point from another, so great is the magnitude of the lines terminated by the points. And this is the meaning of being equally situated between its extremes. For if you take two points in a circumference, or in any other certain line, the space of line which is included between these, exceeds their distance from each other; and every line, besides a right one, appears to suffer this property. Hence, according to a common conception, the vulgar also say, that he who walks by a right line, performs only a necessary journey: but that they necessarily wander much, who do not proceed in a right line. But Plato thus defines it; a right line is that whose middle parts darken its[133] extremes. For this passion necessarily attends things which have a direct position; but it is not necessary that things situated in the circumference of a circle, or in another interval, should be endued with this property. Hence, the astrologers also say, that the sun then suffers an eclipse when that luminary, the moon, and our eye are in one right line; for it is then darkened through the middle position of the moon between us and its orb. And perhaps, the passion of a right line will evince, that in the things which are, according to processions emanating from causes, the mediums are endued with a power of dividing the distance of the extremes, and their mutual communication with each other. As also, according to regressions, such things as are distant from the extremes, are converted by mediums to their primary causes. But Archimedes defines a right line the least of things having the same bounds. For since, according to Euclid, a right line is equally situated between its points, it is on this account, the least of things having the same bounds: for if a less line could be given, it would not lie equally between its extremes: but all the other definitions of a right line, fall into the same conclusions; as for instance, that it is constituted in its extremities, and that one part of it is not in its subject plane, but another, in one more sublime: and that all its parts similarly agree to all: and that its extremes abiding, it also abides. Lastly, that it does not perfect figure, with one line similar in species to itself: for all these definitions express the property of a right line, which it possesses from the simplicity of its essence, and from its having one progression the shortest of all from one extremity to another. And thus much concerning the definitions of a right line. But again, Geminus divides a line first into an incomposite and composite; calling a composite, that which is refracted, and forms an angle; but all the rest of them, he denominates incomposites. Afterwards, he divides a composite line into that which produces figure, and that which may be infinitely extended. And he calls that which produces figure, a circular line, and the line of a shield[145], and that which is similar to an ivy leaf[146]; but that which is not effective of figure, the section of a rectangular and obtuse angular cone, the line similar to a[134] shell[147], the right line, and all of that kind. And again, after another manner, of the incomposite line, one sort is simple, but the other mixt. And of the simple, one produces figure, as the circular; but the other is indefinite, as the right line. But of the mixt, one subsists in planes, but the other in solids. And of that which is in planes, one coincides in itself, as the figure of the ivy leaf, which is called the cissoid; but the other may be produced in infinitum, as the helix. But of that which is in solids, one may be considered in the sections of solids; but the other as consisting about the solids themselves. For the helix, indeed, which is described about a sphere or a cone, consists about solids; but conic, or spirical sections are generated from a particular section of solids. But, with respect to these sections, the conic were invented by Mænechmus, which also Eratosthenes relating, says,
But the spiric by Perseus, who composed an epigram on their invention, to this purpose, “When Perseus had invented three spiral lines in five sections, he sacrificed to the gods on the occasion.” And the three sections of a cone, are the parabola, hyperbola, and ellipsis: but of spiral sections, one kind is twisted and involved, like the fetlock of a horse; but another is dilated in the middle, and deficient in each extremity: and another which is oblong, has less space in the middle, but is dilated on each side. But the multitude of the other mixt lines is infinite. For there is an innumerable multitude of solid figures, from which there are constituted multiform sections. For a right line, while it is circularly moved[148], does not make a certain determinate superficies, nor yet conical, nor conchoidal lines, nor circumferences themselves. Hence, if these solids are multifariously cut, they will exhibit various species of lines. Lastly, of those lines which consist about solids, some are of similar parts, as the helixes[135] about a cylinder; but others of dissimilar parts, as all the rest. From these divisions, therefore, we may collect, that there are only three lines of similar parts, the right, the circular, and the cylindric helix. The two simple ones, indeed, existing in a plane, but the one mixt, about a solid. And this Geminus evidently demonstrates, when he shews, that if two right lines are extended from one point, to a line of similar parts, so as to make equal angles upon that line, they shall be equal to each other. And the demonstrations of this may be received by the studious, from his volumes; since in these he delivers the origin of spiral, conchoidal, and cissoidal lines. But we have barely related the names and divisions of these lines, for the purpose of exciting the ingenious to their investigation; as we think, that an accurate enquiry after the method of detecting the properties of each, would be superfluous in the present undertaking: since the geometrician only unfolds to us in this work, simple and primary lines, i.e. the right line, in the present definition; but a circular line, in the tradition of a circle. For he then says, that the line terminating the circle, is the circumference. But he makes no mention of mixt lines, though he was well acquainted with mixt angles, I mean, the semi-circular and cornicular: as also with plane mixt figures, i.e. segments and sectors; and with solids, viz. cones and cylinders. Of each of the rest, therefore, he delivers three species; but of lines only two, i. e. the right and circular: for he thought it requisite in discourses concerning things simple, to assume simple species; and all the rest are more composite than lines. Hence, in imitation of the geometrician, we also shall terminate their explanation with simple lines.
A Superficies is that which has only Length and Breadth.
After a point and a line, a superficies is placed, which is distant by a twofold interval, length and breadth. But this also remaining destitute of thickness or bulk, possesses a nature more simple than body, which is distant by a triple dimension. On which account the geometrician adds to the two intervals the particle only,[136] because the third interval does not exist in superficies. And this is equivalent to a negation of bulk, as here also he shews the excellency of superficies compared to a solid with respect to simplicity, by negation, or by an addition equivalent to negation: but the diminution which it possesses, if compared with the preceding terms, by the affirmations themselves. But others define a superficies to be the boundary of body, which is almost affirming the same as the definition of Euclid; since that which terminates is exceeded in one dimension, by that which is terminated. And others, a magnitude different by two intervals. Lastly, others declaring the same affection, form its assignation in a somewhat different manner. But they say we have a knowledge of superficies when we measure fields, and distinguish their extremities according to length and breadth; but that we receive a certain sensation of it, when we behold shadows. For as they are without bulk, because they cannot penetrate into the interior part of the earth, they have only length and breadth. But the Pythagoreans say, that it is assimilated to the triad; because the ternary is by far the first cause to all the figures; which a superficies contains. For a circle, which is the principle of orbicular figures, occultly possesses the ternary, by its centre, interval, and circumference. But a triangle, which ranks as the first among all right-lined figures, on every side evinces that it is enclosed by the triad, and receives its form from its perfect nature.
The Extremities of a Superficies are Lines.
From these also, as images, we may understand, that things more simple procure bound and an end to every one of their proximate natures: for soul perfects and determines the operations of nature; and nature the motion of bodies. And prior to these, intellect measures the convolutions of soul; and unity the life of intellect; for that is the measure of all. Just as in these also, a solid is terminated by a superficies; but a superficies by a line; and a line by a point; for that is the boundary of them all. Hence, the line existing[137] uniformly in immaterial forms and impartible reasons, terminates and restrains the various motion of a superficies in its progression, and proximately unites its infinity. But in the images of these, when that which bounds supervenes that which is bounded, it causes, by this means, its limitation and bound. But if it should be enquired how lines are the extremities of every superficies, since they are not the extremes of every finite figure; for the superficies of a sphere is terminated indeed, yet not by lines, but by itself? In answer to this, we must say, that by receiving a superficies so far as it is distant by a twofold interval, we shall find it terminated by lines according to length and breadth. But if we behold a spherical superficies, we must receive it as that which is endued with figure; which possesses another quality, and conjoins the end with the beginning; and loses its two extremities in the comprehensive embraces of one: and this one extremity subsists in capacity only, and not in energy.
A Plane Superficies is that which is equally situated between its bounding Lines.
It was not agreeable to the ancient philosophers to establish a plane species of superficies; but they considered superficies in general, as the representative of magnitude, which is distant by a twofold interval. For thus the divine Plato[149] says, that geometry is contemplative of planes, opposing it in division to stereometry, as if a plane and a superficies were the same. And this was likewise the opinion of the demoniacal Aristotle[150]. But Euclid and his followers consider superficies as a genus, but a plane as its species, in the same manner as rectitude of a line. And on this account he defines a plane separate from a superficies, after the similitude of a right line. For he defines this last as equal to the space, placed between its points. And in like manner, he says, that two right lines being given, a plane superficies occupies a place equal to the space situated between those two lines.[138] For this is equally situated between its lines; and others also explaining the same boundary, assert that it is constituted in its extremities. But others define it as that to all the parts of which a right line may be adapted[151]. But perhaps others will say, that it is the shortest of superficies, having the same boundaries; and that its middle parts darken its extremities; and that all the definitions of a right line may be transferred into a plane superficies, by only changing the genus: since a right, circular, and mixt line, commencing from lines, arrive even at solids, as we have asserted above; for they are proportionally, both in superficies and solids. Hence also, Parmenides says, that every figure is either right, or circular, or mixt. But if you wish to consider the right in superficies, take a plane, to which a right line agrees in various ways; but if a circular receive a spherical superficies; and if a mixt, a conic or cylindric, or some one of that genus. But it is requisite (says Geminus) since a line, and also a superficies is called mixt, to know the measure of mixture, because it is various. For mixture in lines, is neither by composition, nor by temperament only: since, indeed, a helix is mixed, yet one part of it is not straight, and another part circular, like those things which are mixed by composition: nor if a helix is cut after any manner, does it exhibit an image of things simple, such as those which are mixed through temperament; but in these the extremes are, at the same time, corrupted and confused. Hence, Theodorus the mathematician, does not rightly perceive, in thinking that this mixture is in lines. But mixture in superficies, is neither by composition, nor by confusion; but subsists rather by a certain temperament. For conceiving a circle in a subject plane, and a point on high, and producing a right line from the point to the circumference of the circle, the revolution of this line will produce a conical superficies which is mixt. And we again resolve it into its simple elements, by a parallel section: for by drawing[139] a section between the vertex and the base, which shall cut the plane of the generative right line, we effect a circular line. But the idea of lines, shews that the mode of mixture is not by temperament; for neither does it send us back to the simple nature of elements: on the contrary, when superficies are cut, they immediately exhibit to us their producing lines. The mode of mixture, therefore, is not the same in lines and superficies. But as among lines there were some simple, that is, the right and circular, of which the vulgar also possess an anticipated knowledge without any previous instruction; but the species of mixt lines require a more artificial apprehension: so among superficies, we possess an innate notion of those which are especially elementary, the plane and spherical; but science and its reason investigates the variety of those which are composed through mixture. But this is an admirable property of superficies, that their mixture in generation is oftentimes produced from a circular line; and this also happens to a spiral superficies. For this is understood by the revolution of a circle remaining erect, and turning itself about the same point which is not its centre. And on this account, a spiral also is threefold; for its centre is either in a circumference, or within, or external to a circumference. If the centre is in the circumference, a continued spiral is produced: if within the circumference, an intangled one; if without, a divided one. And there are three spiral sections corresponding to these three differences. But every spiral line is mixt, although the motion from which it is produced is one and circular. And mixt superficies are produced as well from simple lines, (as we have said,) while they are moved with a motion of this kind, as from mixt lines. Since, therefore, there are three conic lines, they produce four mixt superficies, which they call conoids. For a rectangular conoid, is produced from the revolution of the parabola about its axis: but that which is formed by the ellipsis, is called a spheroid; and is the revolution is made about the greater axis, it is an oblong; but if about the lesser a broad spheroid. Lastly, an obtuse-angled conoid is generated from the revolution of the hyperbola. But it is requisite to know, that sometimes we arrive at the knowledge of superficies from lines, and sometimes the contrary; for from conical and spiral superficies, we apprehend conical and spiral lines. Besides,[140] this also must be previously received concerning the difference of lines and superficies, that there are three lines of similar parts (as we have already observed), but only two superficies, the plane and the spherical. For this is not true of the cylindric, since all parts of the cylindric superficies cannot agree to all. And thus much concerning the differences of superficies, one of which the geometrician having chosen (I mean the plane), this also he has defined; and in this, as a subject, he contemplates figures, and their attendant passions: for his discourse is more copious in this than in other superficies: since, indeed, we may understand right lines, and circles, and helixes in a plane; also the sections of circles and right lines, contacts, and applications, and the constructions of angles of every kind. But in other superficies, all these cannot be beheld. For how in one that is spherical, can we apprehend a right line, or a right-lined angle? How, lastly, in a conic or cylindric superficies, can we behold sections of circles or right lines? Not undeservedly, therefore, does he both define this superficies, and discuss his geometrical concerns, by exhibiting every thing in this as in a subject; for from hence he calls the present treatise plane. And, after this manner, it is requisite to understand that which is plane, as projected and constituted before the eyes: but cogitation as describing all things in this, the phantasy corresponding to a plane mirror, and the reasons resident in cogitation as dropping their images[152] into its shadowy receptacle.
[153]A Plane Angle, is the inclination of two Lines to each other in a Plane, which meet together, but are not in the same direction.
Some of the ancient philosophers, placing an angle in the predicament of relation, have said, that it is the mutual inclination of lines or planes to each other. But others, including this in quality,[141] as well as rectitude and obliquity, say, that it is a certain passion of a superficies or a solid. And others, referring it to quantity, confess that it is superficies or a solid. For the angle which subsists in superficies is divided by a line; but that which is in solids, by a superficies. But (say they) that which is divided by these, is no other than magnitude, and this is not linear, since a line is divided by a point; and therefore it follows that it must be either a superficies or a solid. But if it is magnitude, and all finite magnitudes of the same kind have a mutual proportion; all angles of the same kind, i. e. which subsist in superficies, will have a mutual proportion. And hence, the cornicular will be proportionable to a right-lined angle. But things which have a mutual proportion, may, by multiplication, exceed each other; and therefore it may be possible for the cornicular to exceed a right-lined angle, which, it is well known, is impossible, since it is shewn to be less than every right-lined angle. But if it is quality alone, like heat and cold, how is it divisible into equal parts? For equality, inequality, and divisibility, are not less resident in angles than in magnitudes; but they are, in like manner, essential. But if the things in which these are essentially inherent, are quantities, and not qualities, it is manifest that angles also are not qualities. Since the more and the less are the proper passions of quality[154], but not equal and unequal. On this hypothesis, therefore, angles ought not to be called unequal, and this greater, but the other less; but they ought to be denominated dissimilars, and one more an angle, but the other less. But that these appellations are foreign from the essence of mathematical concerns, is obvious to every one: for every angle receives the same definition, nor is this more an angle, but that less. Thirdly, if an angle is inclination, and belongs to the category of[142] relation, it must follow, that from the existence of one inclination, there will also be one angle, and not more than one. For if it is nothing else than the relation of lines or planes, how is it possible there can be one relation of lines or planes, but many angles? If, therefore, we conceive a cone cut by a triangle from the vertex to the base, we shall behold one inclination of the triangular lines in the semicone to the vertex; but two distinct angles: one of which is plane, I mean that of the triangle; but the other subsists in the mixt superficies of the cone, and both are comprehended by the two triangular lines. The relation, therefore, of these, do not make the angle. Again, if is necessary to call an angle either quality or quantity, or relation; for figures, indeed, are qualities, but their mutual proportions belong to relation. It is necessary, therefore, that an angle should be reduced under one of these three genera. Such doubts, then, arising concerning an angle, and Euclid calling it inclination, but Apollonius the collection of a superficies, or a solid in one point, under a refracted line or superficies (for he seems to define every angle universally), we shall affirm, agreeable to the sentiments of our preceptor Syrianus, that an angle is of itself none of the aforesaid; but is constituted from the concurrence of them all. And that, on this account, a doubt arises among those who regard one category alone. But this is not peculiar to an angle, but is likewise the property of a triangle. For this, too, participates of quantity, and is called equal and unequal; because it has to quantity the proportion of matter. But quality also, is present with this, in consequence of its figure (since triangles are called as well similar as equal); but it possesses this from one category, and that from another. Hence, an angle is perfectly indigent of quantity, the subject of magnitude. But it is also indigent of quality, by which it possesses, as it were, its proper form and figure, Lastly, it is indigent of the relation of lines terminating, or of superficies comprehending its form. So that an angle consists from all these, yet is not any one of them in particular. And it is indeed divisible, and capable of receiving equality and inequality, according to the quantity which it contains. But it is not compelled to admit the proportion of magnitudes of the same kind, since it has also a peculiar quantity, by which angles are also incapable of a comparison with each other. Nor[143] can one inclination perfect one angle: since the quantity also, which is placed between the inclined lines, completes its essence. If then we regard these distinctions, we shall dissolve all absurdities, and discover that the property of an angle is not the collection of a superficies or solid, according to Apollonius (since these also complete its essence,) but that it is nothing else than a superficies itself, collected into one point, and comprehended by inclined lines, or by one line inclined to itself: and that a solid angle is the collection of superficies mutually inclined to each other. Hence, we shall find that a formed quantum, constituted in a certain relation, supplies its perfect definition. And thus much we have thought requisite to assert concerning the substance of angles, previously contemplating the common essence of every triangle, before we divide it into species. But since there are three opinions of an angle, Eudemus the Peripatetic, who composed a book concerning an angle, affirms that it is quality. For, considering the origin of an angle, he says that it is nothing else than the fraction of lines: because, if rectitude is quality, fraction also will be quality. And hence, since its generation is in quality, an angle will be entirely quality. But Euclid, and those who call it inclination, place it in the category of relation. But they call it quantity, who say that it is the first interval under a point, that is immediately subsisting after a point. In the number of which is Plutarch, who constrains Apollonius also into the same opinion. For it is requisite (says he) there should be some first interval, under the inclination of containing lines or superficies. But since the interval, which is under a point, is continuous, it is not possible that a first interval can be assumed; since every interval is divisible in infinitum. Besides, if we any how distinguish a first interval, and through it draw a right line, a triangle is produced, and not one angle. But Carpus Antiochenus says, that an angle is quantity, and is the distance of its comprehending lines, or superficies; and that this is distant by one interval, and yet an angle is not on that account a line: since it is not true that every thing which is distant by only one interval, is a line. But this surely is the most absurd of all, that there should be any magnitude except a line, which is distant only by one interval. And thus much concerning the nature of an angle. But with respect to the division of[144] angles, some consist in superficies, but others in solids. And of those which are in superficies, some are in simple ones, but others in such as are mixt. For an angle may be produced in a cylindric, conic, spherical, and plane superficies. But of those which consist in simple superficies, some are constituted in the spherical; but others in the plane. For the zodiac itself forms angles, dividing the equinoctial in two parts, at the vertex of the cutting superficies. And angles of this kind subsist in a spherical superficies. But of those which are in planes, some are comprehended by simple lines, others by mixt ones; and others, again, by both. For in the shield-like figure[155], an angle is comprehended by the axis, and the line of the shield: but one of these lines is mixt, and the other simple. But if a circle cuts the shield, the angle will be comprehended by the circumference, and the ellipsis. And when cissoids, or lines similar to an ivy leaf, closing in one point like the leaves of ivy (from whence they derive their appellation) make an angle, such an angle is comprehended by mixt lines. Also, when the hippopede, or line familiar to the foot of a mare, which is one of the spirals, inclining to another line, forms an angle, it is comprehended by mixt lines. Lastly, the angles contained by a circumference and a right line, are comprehended by simple lines. But of these again, some are contained by such as are similar in species, but others by such as are dissimilar. For two circumferences, mutually cutting, or touching each other, produce angles: and these triple, for they are either on both sides convex, when the convexities of the circumferences are external: or on both sides concave, when both the concavities are external; which they call sistroides; or mixt from convex and concave lines, as the lines called lunulas. But besides this, angles are contained in a twofold manner, by a right line and a circumference: for they are either contained by a right line, and a concave circumference, as the semi-circular angle; or by a right line and a convex circumference, as the cornicular angle. But all those which are comprehended by two right lines, are called rectilinear angles, which have likewise a triple difference[156]. The geometrician, therefore, in the present hypothesis, defines all those angles which are constituted in plane superficies, and gives them the common name of[145] a plane angle. And the genus of these he denominates inclination: but the place, the plane itself, for angles have position: but their origin such, that it is requisite there should be two lines at least, and not three as in a solid. And that these should touch each other, and by touching, must not lie in a right line, as an angle is the inclination and comprehension of lines: but is not distance only, according to one interval. But if we examine this definition, in the first place it appears that it does not admit, an angle can be perfected by one line; though a cissoid, which is but one, perfects an angle. And, in like manner, the hippopede. For we call the whole a cissoid, and not its portions (lest any one should say, that the conjunction of these forms an angle) and the whole a spiral, but not its parts. Each, therefore, since it is one, forms an angle to itself, and not to another. But after this, he is faulty, in defining an angle to be inclination. For how, on this hypothesis, will there be two angles, from one inclination? How can we call angles equal and unequal? And whatever else is usually objected against this opinion. Thirdly, and lastly, that part of the definition, which says, and not placed in a right line, is superfluous in certain angles, as in those which are formed from orbicular lines. For without the assistance of this part, the definition is perfect; since the inclination of one of the lines to the other, forms the angle. And it is not possible that orbicular angles should be placed in a right line. And thus much we have thought proper to say concerning the definition of Euclid; partly, indeed, interpreting, and partly doubting its truth.
But when the Lines containing the Angle, are right, the Angle is called Rectilinear.
An angle is the symbol and image of the connection and compression, which subsists in the divine genera, and of that order which collects divisibles into one, particles into an impartible nature, and the many into conciliating community. For it is the bond of a multitude of lines and superficies, the collector of magnitude into the[146] impartibility of points, and the comprehender of every figure which is composed by its confining nature. On which account, the oracles[157] call the angular junctions of figures, knots, so far as they bring with them an image of connecting union, and divine conjunctions, by which discrete natures mutually cohere with each other. The angles, therefore, subsisting in superficies, express the more immaterial, simple, and perfect unions which superficies contain: but those which are in solids, represent the unions, which proceed even to inferiors, and supply a community to things disjunct, and a construction of the same nature, to things which on every side receive a perfect partition. But of the angles in superficies, some shadow forth primary and unmixt unions; but others, such as comprehend in themselves, an infinity of progressions. And some, indeed, are the sources of union to intellectual forms; but others, to sensible reasons; and others, again, are copulative of those forms which obtain between these, a middle situation. Hence, the angles which are made from circumferences, imitate those causes which envelop intellectual variety in coercive union; for circumferences, hastening to coalesce with each other, are images of intellect, and intellectual forms. On the contrary, rectilineal angles, are the symbols of those unions which preside over sensibles, and afford a conjunction of the reasons subsisting in these: but mixt angles represent the preservers of the communion, as well of sensible, as of intellectual forms, according to one immoveable union. It is requisite, therefore, by regarding these paradigms, or exemplars, to render the causes of each. For among the Pythagoreans we shall find various angles dedicated to various gods. Thus, Philolaus, consecrates to some a triangular, but to others a quadrangular angle; and to others, again, different angles. Likewise, he permits the same to many gods, and many to the same god, according to the different powers which they contain. And with a view to this, and to the demiurgic triangle, which is the primary cause of all the ornament of the elements, it appears to me, that Theodorus Asinæus the philosopher, constitutes some of the gods, according to sides; but others, according to angles. The first, indeed, supplying progression and power; but the second, the conjunction of the universe, and the collection of progressive natures[147] again into one. But these, indeed, direct us to the knowledge of the things which are. And we must not wonder that lines are here said to contain an angle. For the one and impartible nature which is found in these, is adventitious: but in the gods themselves, and in true beings, the whole, and impartible good, precedes things many, and divided.
When a Right Line standing on a Right Line, makes the successive Angles on each side equal to one another, each of the equal Angles, is a Right Angle; and the insisting Right Line, is called a Perpendicular to that upon which it stands.
An Obtuse Angle is that which is greater than a Right Angle.
But an Acute Angle, is that which is less than a Right Angle.
These are the triple species of angles, which Socrates speaks of in the Republic, and which are received by geometricians from hypothesis; a right-line constituting these angles, according to a division into species; I mean, the right, the obtuse, and the acute. The first of these being defined by equality, identity and similitude; but the others being composed through the nature of the greater and the lesser; and lastly, through inequality and diversity, and through the more and the less, indeterminately assumed. But many geometricians, are unable to render a reason of this division, and use the assertion, that there are three angles, as an hypothesis[158]. So that,[148] when we interrogate them concerning its cause, they answer, this is not to be required of them as geometricians. However, the Pythagoreans, referring the solution of this triple distribution to principles, are not wanting in rendering the causes of this difference of right-lined angles. For, since one of the principles subsists according to bound, and is the cause of limitation, identity, and equality, and lastly, of the whole of a better co-ordination: but the other is of an infinite nature, and confers on its progeny, a progression to infinity, increase, and decrease, inequality, and diversity of every kind, and entirely presides over the worse series; hence, with great propriety, since the principles of a right-lined angle are constituted by these, the reason proceeding from bound, produces a right angle, one, with respect to the equality of every right angle, endued with similitude, always finite and determinate, ever abiding the same, and neither receiving increment nor decrease. But the reason proceeding from infinity, since it is the second in order, and of a dyadic nature, produces twofold angles about the right angle, distinguished by inequality, according to the nature of the greater and the lesser, and possessing an infinite motion, according to the more and the less, since the one becomes more or less obtuse; but the other more or less acute. Hence, in consequence of this reason, they ascribe right angles to the pure and immaculate gods of the divine ornaments, and divine powers which proceed into the universe, as the authors of the invariable providence of inferiors; for rectitude, and an inflexibility and immutability to subordinate natures accords with these gods: but they affirm, that the obtuse and acute angles should be ascribed to the gods, who afford progression, and motion, and a variety of powers. Since obtuseness is the image of an expanded progression of forms; but acuteness possesses a similitude to the cause dividing and moving the universe. But likewise, among the things which are, rectitude is, indeed, similar to essence, preserving the same bound of its being; but the obtuse and acute, shadow forth the nature of accidents. For these receive the more and the less, and are indefinitely changed without ceasing. Hence, with great propriety, they exhort the soul to make her descent into generation, according to this invariable species of the right angle, by not verging to this part more than to that; and by not affecting[149] some things more, and others less. For the distribution of a certain convenience and sympathy of nature, draws it down into material error, and indefinite variety[159]. A perpendicular line is, therefore, the symbol of inflexibility, purity, immaculate, and invariable power, and every thing of this kind. But it is likewise the symbol of divine and intellectual measure: since we measure the altitudes of figures by a perpendicular, and define other rectilineal angles by their relation to a right angle, as by themselves they are indefinite and indeterminate. For they are beheld subsisting in excess and defect, each of which is, by itself, indefinite. Hence they say, that virtue also stands according to rectitude; but that vice subsists according to the infinity of the obtuse and acute, that it produces excesses and defects, and that the more and the less exhibit its immoderation, and inordinate nature. Of rectilineal angles, therefore, we must establish the right angle, as the image of perfection, and invariable energy, of limitation, intellectual bound, and the like; but the obtuse and acute, as shadowing forth infinite motion, unceasing progression, division, partition and infinity. And thus much for the theological speculation of angles. But here we must take notice, that the genus is to be added to the definitions of an obtuse and acute angle; for each is right-lined, and the one is greater, but the other less than a right-angle. But it is not absolutely true, that every angle which is less than a right one, is acute. For the cornicular is less than every right-angle, because less than an acute one, yet is not on this account an acute angle. Also, a semi-circular is less than any right-angle, yet is not acute. And the cause of this property is because they are mixt, and not rectilineal angles. Besides, many curve-lined angles appear greater than right-lined angles, yet are not on this account obtuse; because it is requisite that an obtuse should be a right-lined angle. Secondly, as it was the intention of Euclid, to define a right-angle, he considers a right-line standing upon another right-line, and making the angles on each side equal. But he defines an obtuse and acute angle, not from the inclination of a right line to either part, but from their relation to a right-angle.[150] For this is the measure of angles deviating from the right, in the same manner as equality of things unequal. But lines inclined to either part, are innumerable, and not one alone, like a perpendicular. But after this, when he says, (the angles equal to one another) he exhibits to us a specimen of the greatest geometrical diligence; since it is possible that angles may be equal to others, without being right. But when they are equal to one another, it is necessary they should be right. Besides, the word successive appears to me not to be added superfluously, as some have improperly considered it; since it exhibits the reason of rectitude. For it is on this account that each of the angles is right; because, when they are successive, they are equal. And, indeed, the insisting right-line, on account of its inflexibility to either part, is the cause of equality to both, and of rectitude to each. The cause, therefore, of the rectitude of angles, is not absolutely mutual equality, but position in a consequent order, together with equality. But, besides all this, I think it here necessary to call to mind, the purpose of our author; I mean, that he discourses in this place, concerning the angles consisting in one plane. And hence, this definition is not of every perpendicular; but of that which is in one and the same plane. For it is not his present design to define a solid angle. As, therefore, he defines, in this place, a plane angle, so likewise a perpendicular of this kind. Because a solid perpendicular ought not to make right angles to one right-line only; but to all which touch it, and are contained in its subject plane: for this is its necessary peculiarity.
A Bound is that which is the Extremity of any thing[160].
A Bound, in this place, is not to be referred to all magnitudes, for there is a bound and extremity of a line; but to the spaces which are contained in superficies, and to solid bodies. For he now calls a bound, the ambit which terminates and distinguishes every[151] space. And a bound of this kind, he defines to be an extremity: but not after the manner in which a point is called the extremity of a line, but according to its property of including and excluding from circumjacent figures. But this name is proper to geometry in its infant state, by which they measured fields, and preserved their boundaries distinct and without confusion, and from which they arrived at the knowledge of the present science. Since, therefore, Euclid calls the external ambit, a bound, it is not without propriety that he, by this means, defines the extremity of spaces. For by this, every thing comprehended is circumscribed. I say, for example, in a circle, its bound and extremity is the circumference; but itself, a certain plane space: and so of the rest.
A Figure is that which is comprehended by one or more Boundaries.
Because figure is predicated in various ways, and is divided into different species, it is requisite, in the first place, to behold its differences; and afterwards to discourse concerning that figure which is proposed in this Definition. There is, then a certain figure which is constituted by mutation, and is produced from passion, while the recipients of the figure are disturbed, divided, or taken away; while they receive additions, or are altered, or suffer other various affections. There is also a figure, which is produced by the potter’s, or statuary’s art, according to the pre-existent reason, which art itself contains: art, indeed, producing the form, but matter receiving from thence, form, and beauty, and elegance. But there are still more noble and more illustrious figures than these, the skilful operations of nature. Some, indeed, existing in the elements under the moon[161], and having a power of comprehending the reasons those elements contain: but others are situated in the celestial regions, distinguishing their powers, and endless revolutions. For the heavenly bodies, both when considered by themselves, and with relation to each other, exhibit an abundant and admirable variety of figures; and at different times they present to our view different forms, bringing with them a splendid image of intellectual[152] species; and, by their elegant and harmonious revolutions, describing the incorporeal and immaterial powers of figures. But there are, again, besides all these, most pure and perfect beauties, the figures of souls, which, because they are full of life, and self-motive, have an existence prior to things moved by another; and which, because they subsist immaterially, and without any dimension, excel the forms which are endued with dimension and matter. In the nature of which we are instructed by Timæus, who has explained to us the demiurgic, and essential figure of souls[162]. But again, the figures of intellects are by far more divine than the figures of souls; for these, on every side, excel partible essences; are every where resplendent with impartible and intellectual light; are prolific, effective, and perfective of the universe; are equally present, and firmly abide in all things; and procure union to the figures of souls; but recall the mutation of sensible figures to the limitation of their proper bound. Lastly, there are, separate from all these, those perfect, uniform, unknown, and ineffable figures of the gods, which are resident, indeed, in the figures of intellects; but jointly terminate all figures, and comprehend all things in their unifying boundaries. The properties of which the theurgic art, also expressing, surrounds various resemblances of the gods, with various figures. And some, indeed, it fashions by characters, in an ineffable manner; for characters of this kind, manifest the unknown powers of the gods: but others it imitates by forms and images; fashioning some of them erect, and others fitting; and some similar to a heart, but others spherical, and others expressed by different figures. And again, some it fabricates of a simple form; but others it composes from a multitude of forms; and some are sacred and venerable; but others are domestic, exhibiting the peculiar gentleness of the gods. And some it constructs of a severe aspect; and lastly, attributes to others, different symbols, according to the similitude and sympathy pertaining to the gods[163]. Since, therefore, figure derives[153] its origin from the gods themselves, it arrives, by a gradual progression, even to inferiors, in these also appearing from primary causes. Since it is requisite to suppose the perfect before the imperfect, and things situated in the stability of their own essence, prior to those which subsist in others, and previous to things full of their own privation, such as preserve their proper nature sincere. Such figures, therefore, as are material, participate of material inelegance, and do not possess a purity convenient to their nature. But the celestial figures are divisible, and subsist in others. And the figures of souls are endued with division, and variety, and involution of every kind; but the figures of intellects, together with immaterial union, possess a progression into multitude. And lastly, the figures of the gods are free, uniform, simple, and generative; they subsist before all things, containing all perfection in themselves, and extending from themselves to all things, the completion of forms. We must not, therefore, listen to, and endure the opinions of many, who affirm, that certain additions, ablations, and alterations, produce sensible figures, (for motions, since they are imperfect, cannot possess the principle and primary cause of effects; nor could the same figures often be produced from contrary motions; for the same form is sometimes generated from addition and detraction,) but we must consider operations of this kind as subservient to other purposes in generation, and derive the perfection[154] of figure from other primogenial causes. Nor must we subscribe to their opinion, who assert that figures destitute of matter can have no subsistence; but those only which appear in matter. Nor to theirs, who acknowledge, indeed, that they are external to matter, but consider them as subsisting alone, according to thought and abstraction. For where shall we preserve in safety, the certainty, beauty, and order of figures, among things which subsist by abstraction? For, since they are of the same kind with sensibles, they are far distant from indubitable and pure certainty. But from whence do they derive the certainty, order, and perfection which they receive? For they either derive it from sensibles (but they have no subsistence in these), or from intelligibles (but in these they are more perfect), since, to say from that which is not, is the most absurd of all. For nature does not produce imperfect figures, and leave the perfect without any subsistence. Nor is it lawful, that our soul should fabricate more certain, perfect, and orderly figures, than intellect and the gods themselves. There are, therefore, prior to sensible figures, self-moving, intellectual, and divine reasons of figures. And we are excited, indeed, from the obscurity of sensible forms, but we produce internal reasons, which are the lucid images of others. And we possess a knowledge of sensible figures, by their exemplars resident in soul (παραδειγματικῶς), but we comprehend by images (εἰκονικῶς) such as are intellectual and divine. For the reasons we contain, emerging from the dark night of oblivion, and propagating themselves in sciential variety, exhibit the forms of the gods, and the uniform bounds of the universe, by which they ineffably convert all things into themselves. In the gods, therefore, there is both an egregious knowledge of universal figures, and a power of generating and constituting all inferiors. But in natures, figures are endued with a power generative of apparent forms; but are destitute of cognition and intellectual perception. And, in particular souls, there is, indeed, an immaterial intellection, and a self-energizing knowledge; but there is wanting a prolific, and efficacious cause. As, therefore, nature, by her forming power presides over sensible figures, in the same manner, soul, by her gnostic energy, drops in the phantasy as in a mirror, the reasons of figures. But the phantasy receiving these in her shadowy forms, and possessing images of the[155] inherent reasons of the soul, affords by these the means of inward conversion to the soul, and of an energy directed to herself, from the spectres of imagination. Just as if any one beholding his image in a mirror, and admiring the power of nature, and his own beauty, should desire to see himself in perfection, and should receive a power of becoming, at the same time, the perceiver, and the thing perceived. For the soul, after this manner, looking abroad into the bright mirror of the phantasy, and surveying the shadowy figures it contains, and admiring their beauty and order, pursues, in consequence of her admiration, the reasons from which these images proceed; and being wonderfully delighted, dismisses their beauty, as conversant about spectres alone; but afterwards seeks her own purer beauty, and desires to pass into her own profound retreats, and there to perceive the circle and the triangle, and all things subsisting together, in an impartible manner, and to insert herself in the objects, to contract her multitude into one; and lastly, to behold the occult and ineffable figures of the gods, seated in the most sacred and divine recesses of her nature. She is likewise desirous of bringing into light, from its awful concealment, the solitary beauty, of the gods, and of perceiving the circle, subsisting in its true perfection, more impartible than any centre, and the triangle without interval; and lastly, by ascending into an union with herself, of surveying every object which is subject to the power of cognition. The figure, therefore, which is self-motive, precedes that which is moved by another; and the impartible that which is self-motive: but that which is the same with one, precedes the impartible itself. For all things are bounded, when they return to the unities of their nature; since all things pass through these as a divine entrance into being. And thus much for this long digression, which we have delivered according to the sentiments of the Pythagoreans. But the geometrician, contemplating that figure which is seated in the phantasy, and defining this, in the first place, (since this definition agrees with sensibles, in the second place) says, that figure is that which is comprehended by one or more boundaries. For, since he receives it together with matter, and conceives of it as distant with intervals, he does not improperly call it finite and terminated[164]. [Since every thing[156] which contains either intelligible or feasible matter, is allotted an adventitious bound; and is not itself bound, but that which is bounded.] Nor is it the bound of itself; but one of its powers is terminating, and the other terminated. Nor does it subsist in bound itself, but is contained by bound. For figure is joined to quantity, and subsists together with it; and, at the same time, quantity is subjected to figure; but the reason and aspect of that quantity is nothing else than figure and form. Since, indeed, reason terminates quantity, and adds to it a particular character and bound, either simple or composite. For, since this also exhibits the twofold progression of bound and infinite in its proper forms, (in the same manner as the reason of an angle,) it invests the objects of its comprehension with one boundary and simple form, according to bound, but with many, according to infinity[165]. Hence, every thing figured, vindicates to itself either one boundary, or a many. Euclid, therefore, denominating that which is figured and material, and annexed to quantity figure, does not improperly say, that it is contained by one or more terms. But Possidonius defines figure to be concluding bound, separating the reason of figure from quantity; and considering it as the cause of terminating, defining, and comprehending quantity. For that which encloses, is different from that which is enclosed; and bound from that which is bounded. And Possidonius, indeed, seems to regard the external surrounding bound; but Euclid, the whole subject. Hence, the one calls a circle a figure, with relation to its whole plane, and exterior ambit; but the other with relation to its circumference only. And the one defines that which is figured, and which is beheld together with its subject: but the other desires to define the reason of the circle; I mean that which terminates and concludes its quantity. But if any logician, and captious person, should blame the definition of Euclid, because he defines genus from species (for things contained by one or more terms, are the species of figure,) we shall assert, in opposition to such an objection, that genera also pre-occupy in themselves the powers of species. And when men of ancient authority, were willing to manifest genera themselves, from those powers which genera contain, they appeared, indeed, to enter on their design from species, but, in reality, they[157] explained genera from themselves, and from the powers which they contain. The reason of figure, therefore, since it is one, comprehends the differences of many figures, according to the bound and infinity residing in its nature. And he who defined this reason, was not void of understanding, whilst he comprehended in a definition, the differences of the powers it contained. But you will ask, From whence does the reason of figure originate, and by what causes is it perfected? I answer, that it first arises from bound and infinite, and that which is mixed from these. Hence it produces some species from bound, others from infinite, and others from the mixt. And this it accomplishes by bringing the form of bound to circles; but that of infinite, to right lines: and that of the mixt to figures composed from right and circular lines. But, in the second place, this reason is perfected from that totality, which is separated into dissimilar parts. From whence, indeed, it occasions a whole to every form, and each figure is cut into different species. For a circle, and every right-lined figure may be divided, by reason or proportion, into dissimilar figures; which is the business of Euclid in his book of divisions, where he divides one figure into figures similar to each as are given; but another into such as are dissimilar. In the third place, it is invigorated from accumulated multitude, and, on account of this, extends forms of every kind, and produces the multiform reasons of figures. Hence, in propagating itself, it does not cease till it arrives at something last, and has unfolded all the variety of forms. And, as in the intelligible world, one is shewn to abide in that which is; and, at the same time, that which is in one, so likewise, reason exhibits circular in right-lined figures; and on the contrary, rectilinear comprehended in circular figures. And it peculiarly manifests its whole nature in each, and all these in all. Since the whole subsists in all collectively, and in each separate and apart. From that order, therefore, it is endued with this power. In the fourth place, it receives from the first of numbers[166], the measures of the progression of forms. From whence it constitutes all figures according to numbers; some, indeed, according to the more simple, but others according to the more composite. For triangles, quadrangles, quinquangles, and all multangles, proceed in[158] infinitum, together with the mutations of numbers. But the cause of this is, indeed, unknown to the vulgar, though, to those who understand where number and figure subsist, the reason is manifest. Fifthly, it is replete with that division of forms, which divides forms into other similar forms, from another second totality, which is also distributed into similar parts. And by this, a triangular reason is divided into triangles, and a quadrangular reason into quadrangles. And hence, exercising our inward powers, we effect what I have said in images, since it pre-existed by far the first in its principles. But by regarding these distributions, we may render many causes of figures, reducing them to their first principles. And the more common, or geometrical figure, is allotted an order of this kind, and from so many causes, receives the perfection of its nature. But, from hence it advances to the genera of the gods, and is variously attributed according to its various forms, and energizes differently in different gods. To some, indeed, affording more simple figures; but to others, such as are more composite. And to some, again, assigning primary figures, and those which are produced in superficies; but to others (entering the tumor of solid bodies) such figures, as in solids are convenient to themselves. For all figures, indeed, subsist in all, since the forms of the gods are accumulated, and full of universal powers: but, by their peculiarity, they produce one thing according to another. For one possesses all things circularly, another in a triangular manner, but another according to a quadrangular reason. And in a similar manner in solids.
A Circle is a Plane Figure, comprehended by one Line, which is called the Circumference, to which all Right Lines falling from a certain Point within the Figure, are equal to each other.
And that Point is called the Centre of the Circle.
A Circle is the first, most simple, and most perfect of figures. For it excels all solids, because it exists in a more simple place; but it is superior to the figures subsisting in planes, on account of its[159] similitude and identity. And it has a corresponding proportion to bound, and unity, and a better co-ordination of being. Hence, in a distribution of mundane and super-mundane figures, you will always find that the circle is of a diviner nature. For if you make a division into the heavens, and the universal regions of generation, you must assign to the heavens a circular form; but to generation, that of a right line, For whatever among generable natures is circular, descends from the heavens; since generation revolves into itself, through their circumvolutions, and reduces its unstable mutation to a regular and orderly continuance. But if you distribute incorporeal natures into soul and intellect, you will say, that the circle belongs to intellect, and the right line to the soul. And on this account, the soul, by its conversion to intellect, is said to be circularly moved; and it possesses the same proportion to intellect, as generation to the heavens. For it is circularly moved, (says Socrates[167],) because it imitates intellect. But the generation and progression of soul is made according to a right-line. For it is the property, of the soul to apply herself at different times to different forms. But if you wish to divide into body and soul, you must constitute every thing corporeal, according to the right line; but you must assign to every animal a participation of the identity and similitude of the circle. For body is a composite, and is endued with various powers, similar to right-lined figures: but soul is simple and intelligent; self-motive, and self-operative; converted into, and energizing in herself. From whence, indeed, Timæus also, when he had composed the elements of the universe from right-lined figures, assigned to them a circular motion and formation, from that divine soul which is seated in the bosom of the world. And thus, that the circle every where holds the first rank, in respect of other figures, is sufficiently evident from the preceding observations. But it is requisite to survey its whole series, beginning supernally, ending in inferiors, and perfecting all things, according to the aptitude of the natures which receive its alliance. To the gods, therefore, it affords a conversion to their causes, and ineffable union: it occasions their abiding in themselves, prevents their departing from their own beatitude, strengthens their highest unions, as centres desirable to[160] inferior natures; and stably places about these the multitude of the powers which the gods possess, containing them in the simplicity of their essences. But the circle affords to intellectual natures, a perpetual energy in themselves, is the cause of their being filled with knowledge from themselves, and of possessing in their essences, intelligibles contractedly; and of perfecting intellections in themselves. For every intellect, proposes to itself that which is intelligible; and this is as a centre to intellect, about which it continually revolves: for intellect folds itself, and operates about this, and is united within itself on all sides, by universal intellectual energies. But it extends to souls by illumination, a self-vital, and self-motive power, and an ability of turning, and leaping round intellect, and of returning according to proper convolutions, unfolding the impartibility of intellect. Again, the intellectual orders excel souls after the manner of centres, but souls energize circularly about their nature. For every soul, according to its intellectual part, and the supreme one, which is the very flower of its essence, receives a centre: but, according to its multitude, it has a circular revolution, desiring, by this means, to embrace the intellect which it participates. But, to the celestial bodies, the circle affords an assimilation to intellect, equality, a comprehension of the universe, in proper limits, revolutions which take place in determinate measures, a perpetual subsistence, a nature without beginning and end, and every thing of this kind. And to the elements under the concave of the moon’s orb, it is the cause of a period, conversant with mutations; an assimilation to the heavens; that which is without generation, in generated natures; that which abides in things which are moved; and whatever is bounded in partible essences. For all things are perpetual, through the circle of generation; and equability is every where preserved on account of the reciprocation of corruption. Since, if generation did not return, in a circular revolution, in a short space of time, the order, and all the ornament of the elements would vanish. But again, the circle procures to animals and plants, that similitude which is found in generations; for these are produced from seeds, and seeds from these. Hence, generation here, and a circumvolution, alternately takes place, from the imperfect to the perfect, and the contrary; so that corruption subsists together with[161] generation. But, besides this, to unnatural productions it imposes order, and reduces their indeterminate variety to the limitation of bound; and, through this, nature herself is gracefully ornamented in the last vestiges of her powers. Hence, things contrary to nature have a revolution according to determinate numbers, and not only fertility, but also sterility, subsists according to the alternate convolutions of circles (as the discourse of the Muses evinces), and all evils though they are dismissed from the presence of the gods, into the place of mortals, yet these roll round, says Socrates, and to these there is present a circular revolution, and a circular order; so that nothing immoderate and evil is deserted by the gods; but that providence, which is perfective of the universe, reduces also the infinite variety of evils, to bound, and an order convenient to their nature. The circle, therefore, is the cause of ornament to all things, even to the last participations, and leaves nothing destitute of itself, since it supplies beauty, similitude, formation, and perfection to the universe. Hence too, in numbers it contains the middle centres of the whole progression of numbers, which revolves from unity to the decad (or ten). For five and six exhibit a circular power, because, in the progressions from themselves, they return again into themselves, as is evident in the multiplication of these numbers. Multiplication, therefore, is an image of progression, since it is extended into multitude; but an ending in the same species, is an image of regression into themselves. But a circular power affords each of these, exciting, indeed, as from an abiding centre, those causes which are productive of multitude; but converting multitude after the productions to their causes. Two numbers, therefore, having the properties of a circle, possess the middle place between all numbers: of which one, indeed, precedes every convertible genus of males and an odd nature; but the other, recalls every thing feminine and even, and all prolific series, to their proper principles, according to a circular power. And thus much concerning the perfection of the circle. Let us now contemplate the mathematical definition of the circle, which is every way perfect. In the first place, therefore, he defines it a figure, because, indeed, it is finite, and every where comprehended by one limit, and is not of an infinite nature, but associated to bound. Likewise[162] plane, because, since figures are either beheld in superficies, or in solid bodies, a circle is the first of plane figures, excelling solids in simplicity, but possessing the proportion of unity to planes. But comprehended by one line, because it is similar to one, by which it is defined, and because it does not extrinsically receive a variety of surrounding terms. And again, that this line makes all the lines drawn to it from a certain point within equal, because of the figures which are bounded by one line, some have all the lines proceeding from the middle equal; but others not at all. For the ellipsis is comprehended by one line, yet all the lines issuing from the centre, and bounded by is curvature, are not equal, but only two. Also the plane, which is included by the line called a cissoid, has one containing line, yet it does not contain a centre, from which all the lines are equal. But, because the centre in a circle is entirely one point (for there are not many centres of one circle), on this account, the geometrician adds, that lines falling from one point to the bound of the circle, are equal. For there are infinite points within it, but of all these, one only has the power of a centre. And because this one point, from which all the lines drawn to the circumference of the circle are equal, is either within the circle, or without (for every circle has a pole, from which all the lines drawn to its circumference are equal), on this account he adds, of the points within the figure, because, here he receives the centre alone, and not the pole. For he wishes to behold all its properties in one plane, but the pole is more elevated than the subject plane. Hence, he necessarily adds, in the end of the definition, that this point, which is placed within the circle, and to which all right lines drawn from it to the circumference, are equal, is the centre of the circle. For there are only two points of this kind, the pole and the centre. But the former is without, and the other within the plane. Thus, for instance, if you conceive a perpendicular standing on the centre of a circle, its superior extremity is the pole: for all lines drawn from it to the circumference of the circle, are demonstrated to be equal. And, in like manner, in a cone, the vertex of the whole cone, is the pole of the circle at the base. And thus far we have determined what a circle is, and its centre, and what the nature is of its circumference, and the whole circular figure. Again, therefore, from these, let us return[163] to the speculation of their exemplars, contemplating in them the centre, according to one impartible and stable excellence. But the distances from the centre, according to the progressions which are made from one, to multitude infinite in capacity. And the circumference of the circle, according to the regression of the progressions to the centre, by means of which the multitude of powers are rolled round their union, and all of them hasten to its comprehension, and desire to energize about its indivisible embrace. And, as in the circle itself, all things subsist together, the centre, intervals, and external circumference; so in these which are its image, one thing has not an essence pre-existent, and another consequent in time; but all things are, indeed, together, permanency, progression, and regression. But these differ from those, because the former subsist indivisibly, and without any dimension; but the latter with dimension; and in a divisible manner; the centre existing in one place, the lines emanating from the centre, in another; and the external circumference terminating the circle, having a still different situation. But there all things abide in one: for if you regard that which performs the office of a centre, you will find it the receptacle of all things. If the progression distant from the centre, in this, likewise, you will find all things contained. And, in a similar manner, if you regard its regression. When, therefore, you are able to perceive all things subsisting together, and have taken away the defect proceeding from dimension, and have removed from your inward vision, the position about which partition subsists, you will find the true circle, advancing to itself, bounding, and energizing in itself, existing both one and many, and abiding, proceeding, and returning; likewise firmly establishing that part of its essence which is most impartible, and especially singular; but advancing from this according to rectitude, and the infinity which it contains; and rolling itself from itself to one, and exciting itself by similitude and identity to the impartible centre of its nature, and to the occult power of the one which it contains. But this one, which the circle contains, and environs in its bosom, it emulates according to the multitude of its own nature. For that which is convolved, imitates that which abides, and the periphery is as a centre which is distant with interval, and[164] nods to itself, hastening to receive, and to become one with the centre, and to terminate its regress where it received the principle of its progression. For the centre is every where in the place of that which is lovely, and the object of desire, presiding over all things which subsist about its nature, and existing as the beginning and author of all progressions. And this the mathematical centre also expresses, by terminating all the lines falling from itself to the circumference, and by affording to them equality, as an image of proper union. But the oracles likewise define the centre, after this manner: The centre is that from which and[168] to which all the lines to the circumference are equal. Indicating the beginning of the distance of the lines, by the particle from which; but the middle of the circumference by the particle to which: for this, in every part, is joined with the centre. But if it be necessary to declare the first cause, through which a circular figure appears and receives its perfection, I affirm, that it is the supreme order of intelligibles. For the centre, indeed, is assimilated to the cause of bound; but the lines emanating from this, and which are infinite, with respect to themselves, both in multitude and magnitude, represent infinity; and the line which terminates their extension, and conjoins the circular figure with the centre, is similar to that occult ornament, consisting from the intelligible orders; which Orpheus also says, is circularly borne, in the following words, But it is carried with an unwearied energy, according to an infinite circle. For, since it is moved intelligibly, about that which is intelligible, having it for the centre of its motion, it is, with great propriety, said to energize in a circular manner. Hence, from these also, the triadic god[169] proceeds, who contains in himself the cause of the progression of right-lined figures. For on this account, wise men, and the most mystic of theologists, have fabricated his name. [[170]Hence too, it is manifest, that a circle is the first of all figures:] but a triangle is the[165] first of such as are right-lined. Figures, therefore, appear first in the regular ornaments of the gods; but they have a latent subsistence, according to pre-existent causes, in intelligible essences.
A Diameter of a Circle is a certain straight Line, drawn through the Centre, which is terminated both ways by the Circumference of the Circle, and, divides the Circle into two equal Parts.
Euclid here perspicuously shews, that he does not define every diameter, but that which belongs to a circle only. Because there is a diameter of quadrangles and all parallelograms, and likewise of a sphere among solid figures. But in the first of these, it is denominated a diagonal: but in a sphere, the axis; and in circles the diameter only. Indeed, we are accustomed to speak of the axis of an ellipsis, cylinder, and cone; but of a circle, with propriety, the diameter. This, therefore, in its genus, is a right-line; but as there are many right-lines in a circle, as likewise infinite points, one of which is a centre, so this only is called a diameter, which passes through the centre, and neither falls within the circumference, nor transcends its boundary; but is both ways terminated by its comprehensive bound. And these observations exhibit its origin. But that which is added in the end, that it also divides the circle into two equal parts, indicates its proper energy in the circle, exclusive of all other lines drawn through the centre, which are not terminated both ways by the circumference. But they report, that Thales first demonstrated, that the circle was bisected by the diameter. And the cause of this bisection, is the indeclineable transit of the right line, through the centre. For, since it is drawn through the middle, and always preserves the same inflexible motion, according to all its parts, it cuts off equal portions on both sides to the circumference of the circle. But if you desire to exhibit the same mathematically, conceive the diameter drawn, and one part of the circle placed on the[166] other[171]. Then, if it is not equal, it either falls within, or without; but the consequence either of these ways must be, that a less right-line will be equal to a greater. Since all lines from the centre to the circumference are equal. The line, therefore, which tends to the exterior circumference, will be equal to that which tends to the interior. But this is impossible. These parts of the circle, then, agree, and are on this account equal. But here a doubt arises, if two semi-circles are produced by one diameter, and infinite diameters may be drawn through the centre, a double of infinities will take place, according to number. For this is objected[172] by some against the section of magnitudes to infinity. But this we may solve by affirming, that magnitude may, indeed, be divided infinitely, but not into infinites. For this latter mode produces infinites in energy, but the former in capacity only. And the one affords essence to infinite, but the other is the source of its origin alone. Two semi-circles, therefore, subsist together with one diameter, yet there will never be infinite diameters, although they may be infinitely assumed. Hence, there[167] can never be doubles of infinites; but the doubles which are continually produced, are the doubles of finites; for the diameters which are always assumed, are finite in number. And what reason can be assigned why every magnitude should not have finite divisions, since number is prior to magnitudes, defines all their sections, pre-occupies infinity, and always determines the parts which rise into energy, from dormant capacity?
A Semi-circle is the Figure contained by the Diameter, and that Part of the Circumference which is cut off by the Diameter.
But the Centre of the Semi-circle, is the same with that of the Circle.
From the definition of a circle Euclid finds out the nature of the centre, differing from all the other points which the circle contains. But from the centre he defines the diameter, and separates it from the other right lines, which are described within the circle. And from the diameter, he teaches the nature of the semi-circle; and informs us, that it is contained by two terms, always differing from each other, viz. a right-line and a circumference: and that this right-line is not any one indifferently, but the diameter of the circle. For both a less and a greater segment of a circle, are contained by a right-line and circumference; yet these are not semi-circles, because the division of the circle is not made through the centre. All these figures, therefore, are biformed, as a circle was monadic, and are composed[168] from dissimilars. For every figure which is comprehended by two terms, is either contained by two circumferences, as the lunular: or by a right-line and circumference, as the above mentioned figures; or by two mixt lines, as if two ellipses intersect each other (since they enclose a figure, which is intercepted between them), or by a mixt line and circumference, as when a circle cuts an ellipsis; or by a mixt and right-line, as the half of an ellipsis. But a semi-circle is composed from dissimilar lines, yet such as are, at the same time, simple, and touching each other by apposition. Hence, before he defines triadic figures, he, with great propriety, passes from the circle to a biformed figure. For two right-lines can, indeed, never comprehend space. But this may be effected by a right-line and circumference. Likewise by two circumferences, either making angles, as in the lunular figure; or forming a figure without angles, as that which is comprehended by concentric circles. For the middle space intercepted between both, is comprehended by two circumferences; one interior, but the other exterior, and no angle is produced. For they do not mutually intersect, as in the lunular figure, and that which is on both sides convex. But that the centre of the semi-circle is the same with that of the circle, is manifest. For the diameter, containing in itself the centre, completes the semi-circle, and from this all lines drawn to the semi-circumference are equal. For this is a part of the circumference of the circle. But equal right lines proceed from the centre to all parts of the circumference. The centre, therefore, of the circle and semi-circle is one and the same. And it must be observed, that among all figures, this alone contains the centre in its own perimeter, I say, among all plane figures. Hence you may collect, that the centre has three places. For it is either within a figure, as in the circle; or in its perimeter, as in the semi-circle; or without the figure, as in certain conic lines[174]. What then is indicated by the semi-circles, having the same centre with the circle, or of what things does it bear an image, unless that all figures which do not entirely depart from such as are first, but participate them after a manner, may be concentric with them, and participate of the same causes? For the semi-circle communicates with the circle doubly, as well according to the diameter,[169] as according to the circumference. On this account, they possess a centre also in common. And perhaps, after the most simple principles, the semi-circle is assimilated to the second co-ordinations, which participate those principles; and by their relation to them, although imperfectly, and by halves, they are, nevertheless, reduced to that which is, and to their first original cause.
Rectilinear Figures are those which are comprehended by Straight Lines.
Trilateral Figures, or Triangles, by three Straight Lines.
Quadrilateral, by four Straight Lines.
Multilateral Figures, or Polygons, by more than four Straight Lines.
After the monadic figure having the relation of a principle to all figures, and the biformed semi-circle, the progression of right-lined figures in infinitum, according to numbers, is delivered. For on this account also, mention was made of the semi-circle, as communicating according to terms or boundaries; partly, indeed, with the circle, but partly with right-lines: just as the duad is the medium between unity and number. For unity, by composition, produces more than by multiplication; but number, on the contrary, is more increased by multiplication than composition: and the duad, whether multiplied into, or compounded with itself, produces an equal quantity. As, therefore, the duad is the middle of unity and number, so likewise, a semi-circle communicates, according to its base, with right-lines;[170] but according to its circumference, with the circle. But right-lined figures proceed orderly to infinity, attended by number and its bounding power, which begins from the triad. On this account, Euclid also begins from hence[175]. For he says, trilateral and quadrilateral, and the following figures, called by the common name of multilateral: since trilateral figures are also multilaterals; but they have likewise a proper, besides a common denomination. But, as we are but little able to pursue the rest, on account of the infinite progression of numbers, we must be content with a common denomination. But he only makes mention of trilaterals and quadrilaterals, because the triad and tetrad are the first in the order of numbers; the former being a pure odd among the odd; but the latter, an entire even among even numbers. Euclid, therefore, assumes both in the origin of right-lined figures, for the purpose of exhibiting their subsistence, according to all even and odd numbers. Besides, since he is about to teach concerning these in the first book, as especially elementary (I mean triangles and parallelograms) he does not undeservedly, as far as to these, establish a proper enumeration: but he embraces all other right-lined figures by a common name, calling them multilaterals: but of these enough. Again, assuming a more elevated exordium, we must say, that of plane figures, some are contained by simple lines, others by such as are mixt, but others again by both. And of those which are comprehended by simple lines, some are contained by similars in species, as right-lines; but others by dissimilars in species, as semi-circles, and segments, and apsides, which are less than semi-circles. Likewise of those which are contained by similars in species, some are comprehended by a circular line; but others by a right-line. And of those comprehended by a circular line, some are contained by one, others by two, but others by more than two. By one, indeed, the circle itself. But by two, some without angles, as the crowns[176] terminated by concentric circles; but others angular (γεγωνιωμένα) as the lunula.[171] And of those comprehended by more than two, there is an infinite procession. For there are certain figures contained by three and four and succeeding circumferences. Thus, if three circles touch each other, they will intercept a certain trilateral space; but if four, one terminated by four circumferences, and in like manner, by a successive progression. But of those contained by right lines, some are comprehended by three, others by four, and others by a multitude of lines. For neither is space comprehended by two right-lines, nor much more by one right-line. Hence, every space comprehended by one boundary, or by two, is either mixt or circular. And it is mixt in a twofold manner, either because the mixt lines comprehend it, as the space intercepted by the cissoidal line; or because it is contained by lines dissimilar in species, as the apsis: since mingling is twofold, either by apposition or confusion. Every right-lined figure, therefore, is either trilateral, or quadrilateral, or gradually multilateral; but every trilateral, or quadrilateral, or multilateral figure, is not right-lined; since so great a number of sides is also produced from circumferences. And thus much concerning the division of plane figures. But we have already asserted[177], that rectitude of progression is both a symbol of motion and infinity, and that it is peculiar to the generative co-ordinations of the gods, and to the producers of difference, and to the authors of mutation and motion. Right-lined figures, therefore, are peculiar to these gods, who are the principles of the prolific energy of the whole progression of forms. On which account, generation also, was principally adorned by these figures, and is allotted its essence from these, so far as it subsists in continual motion and mutation without end.
[172]
Of three-sided Figures: an Equilateral Triangle is that which has three equal Sides.
An Isosceles Triangle, is that which has only two Sides equal.
A Scalene Triangle, is that which has three unequal Sides.
A Right-angled Triangle is that which has a Right Angle.
An Obtuse-angled Triangle is that which has an Obtuse Angle.
An Acute-angled Triangle is that which has three Acute Angles.
The division of triangles sometimes commences from angles, but sometimes from sides. And that, indeed, which originates from sides, precedes as known; but that from angles follows as a proper distribution. For these three angles alone belong to right-lined figures, viz. the right, the obtuse, and the acute: but the equality and inequality of sides subsist also in non-rectilinear figures. Euclid says, therefore, that of triangles, some are equilateral, others[173] isosceles, and others scalene: for they have either all their sides equal, or all unequal, or only two equal. And again, that of triangles some are right-angled, others obtuse-angled, and others acute-angled. And he defines a right-angled triangle, that which has one right angle, as likewise an obtuse-angled triangle, that which has one obtuse angle: for it is impossible that a triangle can have more than one right, or obtuse angle[178]. But he defines an acute-angled triangle, that which has all its angles acute. For here it is not sufficient that it should have only one acute; since, in this case, all triangles would be acute-angled, as every triangle has necessarily two acute angles[179]. But, to possess three acute angles, is the property of an acute-angled triangle alone. But Euclid appears to me to have made a separate division into angles and sides, from considering this alone, that every triangle is not also trilateral. For there are quadrilateral triangles, which are called by mathematicians themselves (ἀκιδοειδῆ) that is, similar to the point of a spear[180]: but by Zenodorus (κοιλογώνια) that is, having an hollow angle. For on one of the sides of a trilateral figure, constitute two right-lines inwardly; by this means a certain space will be enclosed, which is comprehended by external and internal right-lines, and which has three angles; one, indeed, contained by the external lines; but two comprehended by these and the internal lines, at the extremities in which these lines are conjoined. A figure of this kind, therefore, is a quadrilateral triangle. And hence, it does not immediately follow, that because a figure has three angles (whether they[174] are all acute, or one right, or one obtuse), we shall find it trilateral; for it may be, perhaps, quadrilateral. In like manner, you may also find quadrangles having more than four sides. And therefore, we must not rashly determine the number of sides from the multitude of angles. But of this enough. But the Pythagoreans affirm that the triangle is simply the principle of generation, and of the formation of generable natures. On which account, Timæus says, that natural reasons, as well as those of the construction of the elements, are triangular. For they are distant by a triple interval, are on all sides collective of partible, and variously mutable natures, are replete with material infinity, and bear before themselves the conjunctions of material bodies, loosened and free: as, indeed, triangles also are comprehended by three right-lines, but they possess angles which collect the multitude of lines, and afford to them an adventitious angle and conjunction. With great propriety, therefore, Philolaus has consecrated the angle of a triangle to four gods, Saturn, Pluto, Mars, and Bacchus, comprehending in these the whole quadripartite ornament of the elements descending from the heavens, or from the four segments of the zodiac. For Saturn constitutes an essence wholly humid and frigid; but Mars a nature totally fiery; and Pluto contains the whole terrestrial life; but Bacchus governs a humid and hot generation; of which wine also is a symbol, for this is humid and hot. Hence, all these gods differ according to their operations in inferior concerns: but they are mutually united according to their proper natures. And on this account, Philolaus collects their union according to one angle. But if the differences of triangles contribute to generation, we shall very properly confess that a triangle is the principle and author of the constitution of sublunary natures. For a right angle, indeed, affords them essence, and determines the measure of being; and the reason of a right-angled triangle produces the essence of the elements of generable natures; but an obtuse angle assigns to them universal distance; and the reason of an obtuse-angled triangle increases material forms in magnitude, and in mutation of every kind. But an acute angle effects their divisible nature; and the reason of an acute-angled triangle prepares them to receive infinite division. But simply, a triangular reason constitutes the essence of material bodies distant with interval, and on[175] all sides divisible. And thus much should we speculate concerning the nature of triangles. But from these divisions you may understand, that all the species of triangles are neither more nor less than seven. For the equilateral triangle is one, since it is acute-angled only; but each of the rest is triple. For the isosceles is either right-angled, or obtuse-angled, or acute-angled; and, in like manner, the scalene triangle possesses this triple difference. If then, these have a triple distinction, but the equilateral has but one mode of existence, all the species of triangles will be seven. But again, you will understand the proportion of triangles to the things which are, according to the division of sides; for the equilateral, entirely excelling in equality and simplicity, is allied to divine souls; since it is the measure and equality of things unequal, in the same manner as divinity of all inferior concerns. But the isosceles triangle is allied to the better genera, which govern a material nature, the greater part of which genera is held by the limitation of measure; but their extremes extend to inequality and material immoderation; for the two sides of an isosceles triangle are equal, but the base is unequal. But a scalene triangle symbolizes with partible lives, which are on all sides lame and defective, which prepare themselves for generation, and are replete with matter and material imperfection.
Of Quadrilateral Figures, a Quadrangle or Square is that which has all its Sides equal, and all its Angles Right Angles.
An Oblong is that which has all its Angles right Angles, but has not all its Sides equal.
A Rhombus, is that which has all its Sides equal, but its Angles are not right Angles.
[176]
A Rhomboid is that which has its opposite Sides equal to one another, but all its Sides are not equal, nor its Angles Right Angles.
All other Quadrilateral Figures besides these, are called Trapeziums.
It is requisite that the first division of quadrilateral figures should take place in two numbers; and that some of them should be called parallelograms, but others non-parallelograms. But of parallelograms some are rectangular and equilateral, as quadrangles; but others neither of these, as rhomboids: others again, are rectangular, but not equilateral, as oblongs: but others, on the contrary, are equilateral, but not rectangular, as the rhombuses. For it is requisite either to possess both, viz. equality of sides and rectitude of angles, or neither; or one of these, and this in a twofold respect. Hence a parallelogram has a quadruple subsistence. But of non-parallelograms, some have only two parallel sides, and not the rest; but others have none of their sides parallel. And those are called Trapeziums, but these Trapezoids. But of Trapeziums, some, indeed, have the sides equal, by which the parallel sides of this kind are conjoined; but others unequal; and the former of these are called isosceles trapeziums; but the latter scalene trapeziums. A quadrilateral figure, therefore, is constituted by us according to a seven-fold distribution. For one is a quadrangle; but the other an oblong; the third a rhombus; the fourth a rhomboides; the fifth an isosceles trapezium; the sixth a scalene trapezium; the seventh a trapezoid. But Possidonius makes a perfect division of right-lined quadrilateral figures into so many members; for he establishes seven species of these; as likewise of triangles. But Euclid could not divide into parallelograms and non parallelograms, because he neither mentions parallels, nor teaches us concerning the parallelogram itself. But trapeziums, and all trapezoids, he calls by a common[177] name, describing trapeziums themselves, according to the difference of those four figures[181], in which the property of parallelograms is verified. And this is to have the opposite sides and angles equal. For a quadrangle and an oblong, and a rhombus, have their opposite sides and angles equal. But in a rhomboides he only adds this, that its opposite sides are equal, lest he should define it by negations alone, since he neither calls it equilateral, nor rectangular. For where we want proper appellations, it is necessary to use such as are common. But we should hear Euclid shewing that this is common to all parallelograms. But a rhombus appears to be a quadrangle having its sides moved, and a rhomboides a moved oblong. Hence, according to sides, these do not differ from those; but they vary only according to the obtuseness and acuteness of angles; since the quadrangle and the oblong are rectangular. For if you conceive a quadrangle or an oblong, having its sides drawn in such a manner, that while two of its opposite angles are dilated, the other two are contracted; then the dilated angles will appear obtuse, and the contracted, acute. And the appellation of rhombus[182] seems to have been imposed from motion. For if you conceive a quadrangle moving after the manner of a rhombus, it will appear to you changed in order, according to its angles: just as if a circle is moved after the manner of a sling, it will immediately exhibit the appearance of an ellipsis. But here you may perhaps enquire concerning the quadrangle, why it has this denomination? and why the appellation of quadrangle may not be applied to other quadrilateral figures, as the name of triangle is common to all those which are neither equiangular nor equilateral, and in like manner of quinquangles or pentagons; for the geometrician, in these, adds only the particle an equilateral triangle, or a quinquangle, which is equilateral and equiangular, as if these could not be otherwise than such as they are? But when he mentions a quadrangle, he immediately indicates that it must be equilateral and rectangular. But the reason of this is as follows: a quadrangle alone has the best space, both[178] according to its sides and angles. For each of the latter is right, intercepting a measure of angles, which neither receives intention nor remission. As it excels, therefore, in both respects, it deservedly obtains a common appellation. But a triangle, though it may have equal sides, yet will in this case have all its angles acute, and a quinquangle all its angles obtuse. Since, therefore, of all quadrilateral figures, a quadrangle alone is replete with equality of sides, and rectitude of angles, it was not undeservedly allotted this appellation: for, to excellent forms, we often dedicate the name of the whole. But it appeared also to the Pythagoreans, that this property of quadrilateral figures, principally conveyed an image of a divine essence. For they particularly signified by this, a pure and immaculate order. Since rectitude imitates inflexibility, but equality a firm and permanent power: for motion emanates from inequality, but quiet from equality itself. The gods, therefore, who are the authors to all things of stable disposition, of pure and uncontaminated order, and of indeclinable power, are deservedly manifested as from an image, by a quadrangular figure. But, besides these, Philolaus also, according to another apprehension, calls a quadrangular angle, the angle of Rhea, Ceres and Vesta. For, since a quadrangle constitutes the earth, and is its proximate element, as we learn from Timæus, but the earth herself receives from all these divinities, genital seeds, and prolific powers, he does not unjustly consecrate the angle of a quadrangle to these goddesses, the bestowers of life. For some call both the earth and Ceres, Vesta[183], and they say that Rhea totally participates her nature, and that all generative causes are contained in her essence. Philolaus, therefore, says that a quadrangular angle comprehends, by a certain terrestrial power, one union of the divine genera. But some assimilate a quadrangle to universal virtue, so far as every quadrangle from its perfection has four right angles. Just as we say that each of the virtues is perfect, content with itself, the measure and bound of life, and the middle of every thing which, in morals, corresponds to the obtuse and acute. But it is by no means proper to conceal, that Philolaus attributes a triangular angle to four, but a quadrangular angle to three gods, exhibiting[179] their alternate transition, and the community of all things in all, of odd natures in the even, and of even in the odd. Hence, the tetradic ternary, and the triadic quaternary, participating of prolific and efficacious goods, contain the whole ornament of generable natures, and preserve them in their proper state. From which the duodenary, or the number twelve, is excited to a singular unity, viz. the government of Jupiter. For Philolaus says, that the angle of a dodecagon (or twelve-sided figure) belongs to Jove, so far as Jupiter contains and preserves, by his singular union, the whole number of the duodenary. For also, according to Plato, Jupiter presides over the duodenary[184], and governs and moderates the universe with absolute sway. And thus much we have thought proper to discourse concerning quadrilateral figures, as well declaring the sense of our author, as likewise affording an occasion of more profound inspections to such as desire the knowledge of intelligible and occult essences.
Parallel Right Lines are such as being in the same Plane, and produced both ways infinitely, will in no part mutually coincide.
What the elements of parallels are, and by what accidents in these they may be known, we shall afterwards learn: but what parallel right lines are, he defines in these words: “It is requisite, therefore (says he), that they should be in one plane, and while they are produced both ways have no coincidence, but be extended in infinitum.” For non-parallel lines also, if they are produced to a certain distance, will not coincide. But to be produced infinitely, without coincidence, expresses the property of parallels. Nor yet this absolutely, but to be extended both ways infinitely, and not coincide.[180] For it is possible that non-parallel lines may also be produced one way infinitely, but not the other; since, verging in this part, they are far distant from mutual coincidence in the other. But the reason of this is, because two right-lines cannot comprehend space; for if they verge to each other both ways, this cannot happen. Besides this, he very properly considers the right-lines as subsisting in the same plane. For if the one should be in a subject plane, but the other in one elevated, they will not mutually coincide according to every position, yet they are not on this account parallel. The plane, therefore, should be one, and they should be produced both ways infinitely, and not coincide in either part. For with these conditions, the right-lines will be parallel. And agreeable to this, Euclid defines parallel right-lines. But Posidonius says, parallel lines are such as neither incline nor diverge in one plane; but have all the perpendiculars equal which are drawn from the points of the one to the other. But such lines as make their perpendiculars always greater and less, will some time or other coincide, because they mutually verge to each other. For a perpendicular is capable of bounding the altitudes of spaces, and the distances of lines. On which account, when the perpendiculars are equal, the distances of the right lines are also equal; but when they are greater and less, the distance also becomes greater and less, and they mutually verge in those parts, in which the lesser perpendiculars are found. But it is requisite to know, that non-coincidence does not entirely form parallel lines. For the circumferences of concentric circles do not coincide: but it is likewise requisite that they should be infinitely produced. But this property is not only inherent in right, but also in other lines: for it is possible to conceive spirals described in order about right lines, which if produced infinitely together with the right lines, will never coincide[185]. Geminus, therefore, makes a very proper division in this place, affirming from the beginning, that of lines some are bounded, and contain figure, as the circle and ellipsis, likewise the cissoid, and many others; but others are indeterminate, which may be produced infinitely, as the right-line, and the section of a right-angled, and[181] obtuse angled cone; likewise the conchoid itself. But again, of those which may be produced in infinitum, some comprehend no figure, as the right-line and the conic sections; but others, returning into themselves, and forming figure, may afterwards be infinitely produced. And of these some will not hereafter coincide, which resist coincidence, how far soever they may be produced; but others are coincident, which will some time or other coincide. But of non-coincident lines, some are mutually in one plane; and others not. And of non-coincidents subsisting in one plane, some are always mutually distant by an equal interval; but others always diminish the interval, as an hyperbola in its inclination to a right-line, and likewise the conchoid[186]. For these,[182] though they always diminish the interval, never coincide. And they mutually converge, indeed, but never perfectly nod to each other; which is indeed a theorem in geometry especially admirable, exhibiting certain lines endued with a non-assenting nod. But the right-lines, which are always distant by an equal interval, and which never diminish[183] the space placed between them in one plane, are parallel lines. And thus much we have extracted from the studies of the elegant Geminus, for the purpose of explaining the present definition.
END OF THE FIRST VOLUME.
[1] The Grecian literature of this writer will now prove of real utility; and the graces and the sublimities of Plato will soon be familiarised to the English reader, by a hand that I am persuaded will not appear inferior to his great original. Let me also be permitted to recommend his version of Plotinus on the Beautiful.
[2] i.e. Capable of parts.
[3] i.e. Not capable of parts.
[4] Dr. Young, in his Night Thoughts.
[5] See book the second, of Aristotle’s Metaphysics.
[6] Ennead vi. lib. vii.
[7] In his commentary on the 2d, 12th, and 13th books of Aristotle’s Metaphysics, page 60. A Latin translation only of this invaluable work is extant; but I have fortunately a copy in my possession, with the version every where corrected by the learned Thomas Gale, and with large extracts from the Greek.
[8] See Proclus on Plato’s Theology, p. 226.
[9] Ennead vi. lib. 6.
[10] In giving monadic number a subsistence in opinion, I have followed the distribution of Proclus, in the conclusion of his comment on a point; and, I think, not without sufficient reason. For since monadic numbers are more immaterial than geometrical lines and figures, they must have a more immaterial subsistence. But as they are correspondent to matter, they cannot reside in the essential reasons of the soul; nor can they subsist in the phantasy, because they are superior to geometrical figures. It remains, therefore, that we must place them between διάνοια or cogitation, and the phantasy; and this middle situation is that of opinion. For cogitation, which Plato defines, in his Sophista, to be an inward discourse, without voice, is an energy of the rational soul, extending itself from propositions to conclusions. And, according to Plato, in the same place, opinion is the silent affirmation, or negation of διάνοια, or thought. Hence, says he, “opinion is the conclusion of cogitation; but imagination, the mutual mixture of sense and opinion.” So that opinion may, with great propriety, be said to contain monadic number, to which it bears the proportion of matter. And hence the reason is obvious, why the Pythagoreans called the duad opinion.
i.e. (According to the Pythagoreans) “the immortal gods and earth-born men, call the venerable decad, immutable and unwearied.”
[15] In his Mathematical Lectures, page 48.
[16] In Arithmet. p. 23.
[17] In Aristot. Meta. p. 113. Gr. vel 59. b. Lat.
[18] For the tetrad contains all numbers within its nature, in the manner of an exemplar; and hence it is, that in monadic numbers, 1, 2, 3, 4, are equal to ten.
[19] Notes to Letters on Mind, page 83.
[20] This bright light is no other than that of ideas themselves; which, when it is once enkindled, or rather re-kindled in the soul, becomes the general standard, and criterion of truth. He who possesses this, is no longer the slave of opinion; puzzled with doubts, and lost in the uncertainties of conjecture. Here the fountain of evidence is alone to be found.—This is the true light, whose splendors can alone dispel the darkness of ignorance, and procure for the soul undecaying good, and substantial felicity. Of this I am certain, from my own experience; and happy is he who acquires this invaluable treasure. But let the reader beware of mixing the extravagancies of modern enthusiasm with this exalted illumination. For this light is alone brought into the mind by science, patient reflection, and unwearied meditation: it is not produced by any violent agitation of spirits, or extasy of imagination; for it is far superior to the energies of these: but it is tranquil and steady, intellectual and divine. Avicenna, the Arabian, was well acquainted with this light, as is evident from the beautiful description he gives of it, in the elegant introduction of Ebn Tophail, to the Life of Hai Ebn Yokdhan. “When a man’s desires (says he) are considerably elevated, and he is competently well exercised in these speculations, there will appear to him some small glimmerings of the truth, as it were flashes of lightning, very delightful, which just shine upon him, and then become extinct. Then the more he exercises himself, the oftener will he perceive them, till at last he will become so well acquainted with them, that they will occur to him spontaneously, without any exercise at all; and then as soon as he perceives any thing, he applies himself to the divine essence, so as to retain some impression of it; then something occurs to him on a sudden, whereby he begins to discern the truth in every thing; till through frequent exercise he at last attains to a perfect tranquillity; and that which used to appear to him only by fits and starts, becomes habitual, and that which was only a glimmering before, a constant light; and he obtains a constant and steady knowledge.” He who desires to know more concerning this, and a still brighter light, that arising from an union with the supreme, must consult the eighth book of Plotinus’ fifth Ennead, and the 7th and 9th of the sixth, and his book on the Beautiful, of which I have published a translation.
[21] Lest the superficial reader should think this is nothing more than declamation, let him attend to the following argument. If the soul possesses another eye different from that of sense (and that she does so, the sciences sufficiently evince), there must be, in the nature of things, species accommodated to her perception, different from feasible forms. For if our intellect speculates things which have no real subsistence, such as Mr. Locke’s ideas, its condition must be much more unhappy than that of the sensitive eye, since this is co-ordinated to beings; but intellect would speculate nothing but illusions. Now, if this be absurd, and if we possess an intellectual eye, which is endued with a visive power, there must be forms correspondent and conjoined with its vision; forms immoveable, indeed, by a corporeal motion, but moved by an intellectual energy.
[22] The present section contains an illustration of almost all the first book of Aristotle’s last Analytics. I have for the most part followed the accurate and elegant paraphrase of Themistius, in the execution of this design, as the learned reader will perceive: but I have likewise everywhere added elucidations of my own, and endeavoured to render this valuable work intelligible to the thinking mathematical reader.
[23] See the twenty-eighth proposition of the first book of Euclid’s Elements.
[24] We are informed by Simplicius, in his Commentary on Aristotle’s third Category of Relation, “that though the quadrature of the circle seems to have been unknown to Aristotle, yet, according to Jamblichus, it was known to the Pythagoreans, as appears from the sayings and demonstrations of Sextus Pythagoricus, who received (says he) by succession, the art of demonstration; and after him Archimedes succeeded, who invented the quadrature by a line, which is called the line of Nicomedes. Likewise, Nicomedes attempted to square the circle by a line, which is properly called τεταρτημόριον, or the quadrature. And Apollonius, by a certain line, which he calls the sister of the curve line, similar to a cockle, or tortoise, and which is the same with the quadratix of Nicomedes. Also Carpus wished to square the circle, by a certain line, which he calls simply formed from a twofold motion. And many others, according to Jamblichus, have accomplished this undertaking in various ways.” Thus far Simplicius. In like manner, Boethius, in his Commentary on the same part of Aristotle’s Categories (p. 166.) observes, that the quadrature of the circle was not discovered in Aristotle’s time, but was found out afterwards; the demonstration of which (says he) because it is long, must be omitted in this place. From hence it seems very probable, that the ancient mathematicians applied themselves solely to squaring the circle geometrically, without attempting to accomplish this by an arithmetical calculation. Indeed, nothing can be more ungeometrical than to expect, that if ever the circle be squared, the square to which it is equal must be commensurable with other known rectilineal spaces; for those who are skilled in geometry know that many lines and spaces may be exhibited with the greatest accuracy, geometrically, though they are incapable of being expressed arithmetically, without an infinite series. Agreeable to this, Tacquet well observes (in lib. ii. Geom. Pract. p. 87.) “Denique admonendi hic sunt, qui geometriæ, non satis periti, sibi persuadent ad quadraturam necessarium esse, ut ratio lineæ circularis ad rectam, aut circuli ad quadratum in numeris exhibeatur. Is sane error valde crassus est, et indignus geometrâ, quamvis enim irrationalis esset ea proportio, modo in rectis lineis exhibeatur, reperta erat quadratura.” And that this quadrature is possible geometrically, was not only the opinion of the above mentioned learned and acute geometrician, but likewise of Wallis and Barrow; as may be seen in the Mechanics of the former, p. 517 and in the Mathematical Lectures of the latter, p. 194. But the following discovery will, I hope, convince the liberal geometrical reader, that the quadrature of the circle may be obtained by means of a circle and right-line only, which we have no method of accomplishing by any invention of the ancients or moderns. At least this method, if known to the ancients, is now lost, and though it has been attempted by many of the moderns, it has not been attended with success.
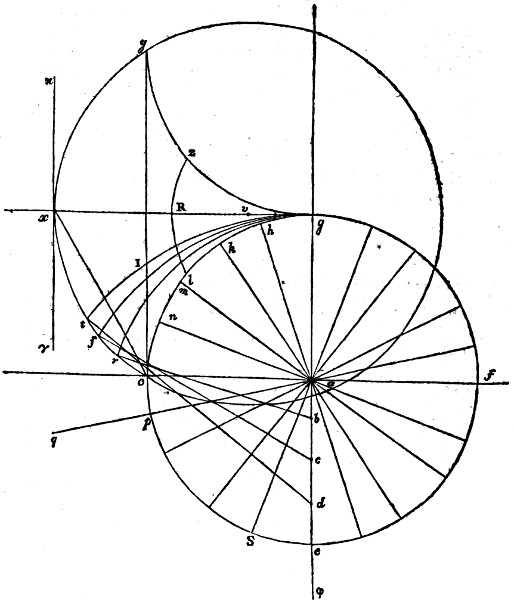
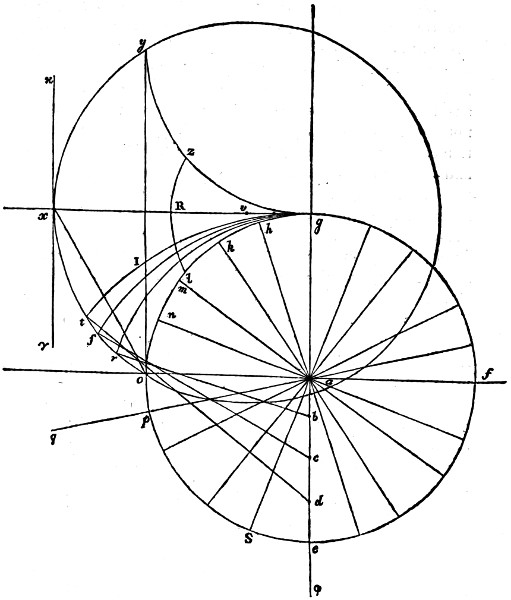
In the circle g o e f, let g o be the quadrantal arch, and the right-line g x its tangent. Then conceive that the central point a flows uniformly along the radius a e, infinitely produced; and that it is endued with an uniform impulsive power. Let it likewise be supposed, that during its flux, radii emanate from it on all sides, which enlarge themselves in proportion to the distance of the point a from its first situation. This being admitted, conceive that the point a by its impulsive power, through the radii a n, a m, &c. acting every where equally on the arch g o, impells it into its equal tangent arch g r. And when, by its uniform motion along the infinite line a φ, it has at the same time arrived at b, the centre of the arch g r, let it impel in a similar manner the arch g r, into its equal tangent arch g s, by acting every where equally through radii equal to b r. Now, if this be conceived to take place infinitely (since a circular line is capable of infinite remission) the arch g o will at length be unbent into its equal, the tangent line g x; and the extreme point o, will describe by such a motion of unbending a circular line o x. For since the same cause, acting every where similarly and equally, produces every where similar and equal effects; and the arch g o, is every where equally remitted or unbent, it will describe a line similar in every part. Now, on account of the simplicity of the impulsive motion, such a line must either be straight or circular; for there are only three lines every where similar, i. e. the right and circular line, and the cylindric helix; but this last, as Proclus well observes in his following Commentary on the fourth definition, is not a simple line, because it is generated by two simple motions, the rectilineal and circular. But the line which bounds more than two equal tangent arches cannot be a right line, as is well known to all geometricians; it is therefore a circular line. It is likewise evident, that this arch o x is concave towards the point g: for if not, it would pass beyond the chord o x, which is absurd. And again, no arch greater than the quadrant can be unbent by this motion: for any one of the radii, as a p beyond g o, has a tendency from, and not to the tangent g x, which last is necessary to our hypothesis. Now if we conceive another quadrantal arch of the circle g o e f, that is g y, touching the former in g to be unbent in the same manner, the arch x y shall be a continuation of the arch x o; for if γ x κ be drawn perpendicular to x g, as in the figure, it shall be a tangent in x to the equal arches y x, x o; because it cannot fall within either, without making the sine of some one of the equal arches, equal to the right-line x g, which would be absurd. And hence we may easily infer, that the centre of the arch y x o, is in the tangent line x g. Hence too, we have an easy method of finding a tangent right-line equal to a quadrantal arch: for having the points y, o given, it is easy to find a third point, as s; and then the circle passing through the three points o, s, y, shall cut off the tangent x g, equal to the quadrantal arch g o. And the point s may be speedily obtained, by describing the arch g s with a radius, having to the radius a g the proportion of 6 to 4; for then g s is the sixth part of its whole circle, and is equal to the arch g o. And thus, from this hypothesis, which, I presume, may be as readily admitted as the increments and decrements of lines in fluxions, the quadrature of the circle may be geometrically obtained; for this is easily found, when a right-line is discovered equal to the periphery of a circle. I am well aware the algebraists will consider it as useless, because it cannot be accommodated to the farrago of an arithmetical calculation; but I hope the lovers of the ancient geometry will deem it deserving an accurate investigation; and if they can find no paralogism in the reasoning, will consider it as a legitimate demonstration.
[25] Axioms have a subsistence prior to that of magnitudes and mathematical numbers, but subordinate to that of ideas; or, in other words, they have a middle situation between essential and mathematical magnitude. For of the reasons subsisting in soul, some are more simple and universal, and have a greater ambit than others, and on this account approach nearer to intellect, and are more manifest and known than such as are more particular. But others are destitute of all these, and receive their completion from more ancient reasons. Hence it is necessary (since conceptions are then true, when they are consonant with things themselves) that there should be some reason, in which the axiom asserting, if from equals you take away equals, &c. is primarily inherent; and which is neither the reason of magnitude, nor number, nor time, but contains all these, and every thing in which this axiom is naturally inherent. Vide Syrian. in Arith. Meta. p. 48.
[26] Geometry, indeed, wishes to speculate the impartible reasons of the soul, but since she cannot use intellections destitute of imagination, she extends her discourses to imaginative forms, and to figures endued with dimension, and by this means speculates immaterial reasons in these; and when imagination is not sufficient for this purpose, she proceeds even to external matter, in which she describes the fair variety of her propositions. But, indeed, even then the principal design of geometry is not to apprehend sensible and external form, but that interior vital one, resident in the mirror of imagination, which the exterior inanimate form imitates, as far as its imperfect nature will admit. Nor yet is it her principal design to be conversant with the imaginative form; but when, on account of the imbecility of her intellection, she cannot receive a form destitute of imagination, she speculates the immaterial reason in the purer form of the phantasy; so that her principal employment is about universal and immaterial forms. Syrian. in Arist. Meta. p. 49.
[27] Syrianus, in his excellent Commentary on Aristotle’s Metaphysics, (which does not so much explain Aristotle, as defend the doctrine of ideas, according to Plato, from the apparent if not real opposition of Aristotle to their existence), informs us that it is the business of wisdom, properly so called, to consider immaterial forms or essences, and their essential accidents. By the method of resolution receiving the principles of being; by a divisive and and definitive method, considering the essences of all things; but by a demonstrative process, concluding concerning the essential properties which substances contain. Hence (says he) because intelligible essences are of the most simple nature, they are neither capable of definition nor demonstration, but are perceived by a simple vision and energy of intellect alone. But middle essences, which are demonstrable, exist according to their inherent properties: since, in the most simple beings, nothing is inherent besides their being. On which account we cannot say that this is their essence, and that something else; and hence they are better than definition and demonstration. But in universal reasons, considered by themselves, and adorning a sensible nature, essential accidents supervene; and hence demonstration is conversant with these. But in material species, individuals, and sensibles, such things as are properly accidents are perceived by the imagination, and are present and absent without the corruption of their subjects. And these again being worse than demonstrable accidents, are apprehended by signs, not indeed by a wise man, considered as wise, but perhaps by physicians, natural philosophers, and all of this kind.
[28] See Note to Chap. i. Book i. of the ensuing Commentaries.
[29] Page 227.
[30] Page 250.
[31] Methodus hæc cum algebrâ speciosâ facilitate contendit, evidentiâ vero et demonstrationum elegantiâ eam longe superare videtur: ut abunde constabit, si quis conferat hanc Apollonii doctrinam de Sectione Rationis cum ejusdem Problematis Analysi Algebraicâ, quam exhibuit clarissimus Wallisius, tom. ii. Operum Math. cap. liv. p. 220.
[32] Verum perpendendum est, aliud esse problema aliqualiter resolutum dare, quod modis variis, plerumque fieri potest, aliud methodo elegantissimâ ipsum efficere; Analysi brevissimâ et simul perspicuâ, Synthesi concinnâ et minime operosâ.
[33] In his Mathematical Lectures, p. 44.
[34] Lib. iv.
[35] Lib. i. p. 30.
[36] In Theæteto.
[37] In his most excellent work on Abstinence, lib. i. p. 22, &c.
[38] See the Excerpta of Ficinus from Proclus, on the first Alcibiades of Plato; his Latin version only of which is extant. Ficini Opera, tom. ii.
[39] Marinus, the author of the ensuing life, was the disciple of Proclus; and his successor in the Athenian school. His philosophical writings were not very numerous, and have not been preserved. A commentary ascribed to him, on Euclid’s data, is still extant; but his most celebrated work, appears to have been, the present life of his master. It is indeed in the original elegant and concise; and may be considered as a very happy specimen of philosophical biography. Every liberal mind must be charmed and elevated with the grandeur and sublimity of character, with which Proclus is presented to our view. If compared with modern philosophical heroes, he appears to be a being of a superior order; and we look back with regret on the glorious period, so well calculated for the growth of the philosophical genius, and the encouragement of exalted merit. We find in his life, no traces of the common frailties of depraved humanity; no instances of meanness, or instability of conduct: but he is uniformly magnificent, and constantly good. I am well aware that this account of him will be considered by many as highly exaggerated; as the result of weak enthusiasm, blind superstition, or gross deception: but this will never be the persuasion of those, who know by experience what elevation of mind and purity of life the Platonic philosophy is capable of procuring; and who truly understand the divine truths contained in his works. And the testimony of the multitude, who measure the merit of other men’s characters by the baseness of their own, is surely not to be regarded. I only add, that our Philosopher flourished 412 years after Christ, according to the accurate chronology of Fabricius; and I would recommend those who desire a variety of critical information concerning Proclus, to the Prolegomena prefixed by that most learned man to his excellent Greek and Latin edition of this work, printed at London in 1703.
[40] Plato in Phædro. Meminit et Plutarch. VIII. Sympos. Suidas in μήτοι. Fabricius.
[41] For a full account of the distribution of the virtues according to the Platonists, consult the sentences of Porphyry, and the Prolegomena of Fabricius to this work.
[42] See the sixth book of his Republic, and the Epinomis.
[43] We are informed by Fabricius, that the Platonic Olympiodorus in his MS. Commentary on the Alcibiades of Plato, divides the orders of the Gods, into ὑπερκόσμιοι, or super-mundane, which are separate from all connection with body; and into ἐγκόσμιοι, or mundane. And that of these, some are οὐράνιοι, or celestial, others αἰθέριοι, or, or etherial, or πύριοι, fiery, others ἀέριοι, or aerial, others ἔνυδροι, or watry, others χθόνιοι, or earthly; and others ὑποταρτάριοι, or subterranean. But among the terrestrial, some are κλιματάρχαι, or governors of climates, others πολιοῦχοι, or rulers over cities, and others lastly κατοικίδιοι, or governors of houses.
[44] This epithet is likewise ascribed by Onomacritus to the Moon, as may be seen in his hymn to that deity; and the reason of which we have given in our notes to that hymn.
[45] Divine visions, and extraordinary circumstances, may be fairly allowed to happen to such exalted geniuses as Proclus; but deserve ridicule when ascribed to the vulgar.
[46] What glorious times! when it was considered as an extraordinary circumstance for a teacher of rhetoric to treat a noble and wealthy pupil as his domestic. When we compare them with the present, we can only exclaim, O tempora! O mores! Philosophy sunk in the ruins of ancient Greece and Rome.
[47] Fabricius rightly observes, that this Olympiodorus is not the same with the Philosopher of that name, whose learned commentaries, on certain books of Plato, are extant in manuscript, in various libraries. As in these, not only Proclus himself, but Damascius, who flourished long after Proclus, is celebrated.
[48] Concerning the various mathematicians of this name, see Fabricius in Bibliotheca Græca.
[49] The word in the original is λογικὰ, which Fabricius rightly conjectures has in this place a more extensive signification than either Logic, or Rhetoric: but I must beg leave to differ from that great critic, in not translating it simply philosophical, as I should rather imagine, Marinus intended to confine it to that part of Aristotle’s works, which comprehends only logic, rhetoric, and poetry. For the verb ἐξεμάνθανω, or to learn, which Marinus uses on this occasion, cannot with propriety be applied to the more abstruse writings of Aristotle.
[50] Hence Proclus was called, by way of eminence, διάδοχος Πλατωνικός, or the Platonic Successor.
[51] Concerning Polletes, see Suidas; and for Melampodes, consult Fabricius in Bibliotheca Græca.
[52] This Syrianus was indeed a most excellent philosopher, as we may be convinced from his commentary on the metaphysics of Aristotle, a Latin translation only of which, by one Hieronimus Bagolinus, was published at Venice in 1558. The Greek is extant, according to Fabricius, in many of the Italian libraries, and in the Johannean library at Hamburg. According to Suidas, he writ a commentary on the whole of Homer in six books; on Plato’s politics, in four books; and on the consent of Orpheus, Pythagoras, and Plato, with the Chaldean Oracles, in ten books. All these are unfortunately lost; and the liberal few, are by this means deprived of treasures of wisdom, which another philosophical age, in some distant revolution, is alone likely to produce.
[53] Socrates, in the 6th book of Plato’s Republic, says, that from great geniuses nothing of a middle kind must be expected; but either great good, or great evil.
[54] The reader will please to take notice, that this great man is not the same with Plutarch the biographer, whose works are so well known; but an Athenian philosopher of a much later period.
[55] Aristotle’s philosophy, when compared with the discipline of Plato is, I think, deservedly considered in this place as bearing the relation of the proteleia to the epopteia in sacred mysteries. Now the proteleia, or things previous to perfection, belong to the initiated, and the mystics; the former of whom were introduced into some lighter ceremonies only: but the mystics, were permitted to be present with certain preliminary and lesser sacred concerns. On the other hand, the epoptæ were admitted into the sanctuary of the greater sacred rites; and became spectators of the symbols, and more interior ceremonies. Aristotle indeed appears to be every where an enemy to the doctrine of ideas, as understood by Plato; though they are doubtless the leading stars of all true philosophy. However, the great excellence of his works, considered as an introduction to the divine theology of Plato, deserves the most unbounded commendation. Agreeable to this, Damascius informs us that Isidorus the philosopher, “when he applied himself to the more holy philosophy of Aristotle, and saw that he trusted more to necessary reasons than to his own proper sense, yet did not entirely employ a divine intellection, was but little solicitous about his doctrine: but that when he had tasted of Plato’s conceptions, he no longer deigned to behold him in the language of Pindar. But hoping he should obtain his desired end, if he could penetrate into the sanctuary of Plato’s mind, he directed to this purpose the whole course of his application.” Photii Bibliotheca. p. 1034.
[56] according to the oracle.
[57] Nothing is more celebrated by the ancients than that strict friendship which subsisted among the Pythagoreans; to the exercise of which they were accustomed to admonish each other, not to divide the god which they contained, as Jamblichus relates, lib. i. c. 33. De Vita Pythagoræ. Indeed, true friendship can alone subsist in souls, properly enlightened with genuine wisdom and virtue; for it then becomes an union of intellects, and must consequently be immortal and divine.
[58] Pythagoras, according to Damascius, said, that friendship was the mother of all the political virtues.
[59] A genuine modern will doubtless consider the whole of Proclus’ religious conduct as ridiculously superstitious. And so, indeed, at first sight, it appears; but he who has penetrated the depths of ancient wisdom, will find in it more than meets the vulgar ear. The religion of the Heathens, has indeed, for many centuries, been the object of ridicule and contempt: yet the author of the present work is not ashamed to own, that he is a perfect convert to it in every particular, so far as it was understood and illustrated by the Pythagoric and Platonic philosophers. Indeed the theology of the ancient, as well as of the modern vulgar, was no doubt full of absurdity; but that of the ancient philosophers, appears to be worthy of the highest commendations, and the most assiduous cultivation. However, the present prevailing opinions, forbid the defence of such a system; for this must be the business of a more enlightened and philosophic age. Besides, the author is not forgetful of Porphyry’s destiny, whose polemical writings were suppressed by the decrees of emperors; and whose arguments in defence of his religion were so very futile and easy of solution, that, as St. Hierom informs us, in his preface on Daniel, Eusebius answered him in twenty-five, and Apollinaris in thirty volumes!
[60] See Proclus on Plato’s Politics, p. 399. Instit. Theolog. num. 196; and the extracts of Ficinus from Proclus’s commentary on the first Alcibiades, p. 246. &c.
[61] Alluding to the beautiful description given of Ulysses, in the 3d book of the Iliad, v. 222.
Which is thus elegantly paraphrased by Mr. Pope.
[62] Concerning Domninus, see Photius and Suidas from Damascius in his Life of Isidorus.
[63] Nicephorus, in his commentary on Synesius de Insomniis, p. 562. informs us, that the hecatic orb, is a golden sphere, which has a sapphire stone included in its middle part, and through its whole extremity, characters and various figures. He adds, that turning this sphere round, they perform invocations, which they call Jyngæ. Thus too, according to Suidas, the magician Julian of Chaldea, and Arnuphis the Egyptian, brought down showers of rain, by a magical power. And by an artifice of this kind, Empedocles was accustomed to restrain the fury of the winds; on which account he was called ἀλεξάνεμος, or a chaser of winds.
[64] No opinion is more celebrated, than that of the metempsychosis of Pythagoras: but perhaps, no doctrine is more generally mistaken. By most of the present day it is exploded as ridiculous; and the few who retain some veneration for its founder, endeavour to destroy the literal, and to confine it to an allegorical meaning. By some of the ancients this mutation was limited to similar bodies: so that they conceived the human soul might transmigrate into various human bodies, but not into those of brutes; and this was the opinion of Hierocles, as may be seen in his comment on the Golden Verses. But why may not the human soul become connected with subordinate as well as with superior lives, by a tendency of inclination? Do not similars love to be united; and is there not in all kinds of life, something similar and common? Hence, when the affections of the soul verge to a baser nature, while connected with a human body, these affections, on the dissolution of such a body, become enveloped as it were, in a brutal nature, and the rational eye, in this case, clouded with perturbations, is oppressed by the irrational energies of the brute, and surveys nothing but the dark phantasms of a degraded imagination. But this doctrine is vindicated by Proclus with his usual subtilty, in his admirable commentary on the Timæus, lib. v. p. 329, as follows, “It is usual, says he, to enquire how souls can descend into brute animals. And some, indeed, think that there are certain similitudes of men to brutes, which they call savage lives: for they by no means think it possible that the rational essence can become the soul of a savage animal. On the contrary, others allow it may be sent into brutes, because all souls are of one and the same kind; so that they may become wolves and panthers, and ichneumons. But true reason, indeed, asserts that the human soul way be lodged in brutes, yet in such a manner, as that it may obtain its own proper life, and that the degraded soul may, as it were, be carried above it, and be bound to the baser nature, by a propensity and similitude of affection. And that this is the only mode of insinuation, we have proved by a multitude of reasons, in our commentaries on the Phædrus. But if it is requisite to take notice, that this is the opinion of Plato, we add, that in his politics, he says, that the soul of Thersites assumed an ape, but not the body of an ape: and in the Phædrus, that the soul descends into a savage life, but not into a savage body; for life is conjoined with its proper soul. And in this place he says it is changed into a brutal nature: for a brutal nature is not a brutal body, but a brutal life.”
[65] Pericles Lydus, a Stoic philosopher.
[66] Vide Pausan. lib. i. Atticorum, cap. 21. et 20.
[67] He means the Christians.
[68] Proclus was born in the year of Christ 412, on the 6th of the Ides of February. But, for the sake of the astrologers, I have subjoined the following figure from the Prolegomena of Fabricius to this life: and though I am not skilled in the art myself, I am persuaded, from the arguments of Plotinus, that it contains many general truths; but when made subservient to particulars, is liable to great inaccuracy and error. In short, its evidence is wholly of a physiognomic nature; for such is the admirable order and connection of things, that throughout the universe, one thing is signified by another, and wholes are after a manner contained in their parts. So that the language of the obscure and profound Heraclitus is perfectly just, when he says, “You must connect the perfect and the imperfect, the agreeing and the disagreeing, the consonant and the dissonant, and out of one all things, and out of all things one.”

A Scheme of the situation of the Stars, such as it was at Byzantium, when the philosopher Proclus was born.
[69] It was formerly the custom of almost all nations, to have their burial places in the suburbs, and not in the city itself.
[70] This eclipse happened, according to Fabricius, in A. C. 484. 19 Cal. Feb. at sun-rise.
[71] All the ancient theologists, among whom Plato holds a distinguished rank, affirmed that the soul was of a certain middle nature and condition between intelligibles and sensibles: agreeable to which doctrine, Plotinus divinely asserts that she is placed in the horizon, or in the boundary and isthmus, as it were, of eternal and mortal natures; and hence, according to the Magi, she is similar to the moon, one of whose parts is lucid, but the other dark. Now the soul, in consequence of this middle condition, must necessarily be the receptacle of all middle energies, both vital and gnostic; so that her knowledge is inferior to the indivisible simplicity of intellectual comprehension, but superior to the impulsive perceptions of sense. Hence the mathematical genera and species reside in her essence, as in their proper and natural region; for they are entirely of a middle nature, as Proclus proves in this and the sixth following chapter. But this doctrine of Plato’s, originally derived from Brontinus and Archytas, is thus elegantly explained by that philosopher, in the concluding part of the sixth book of his Republic. “Socrates, know then, they are, as we say, two (the Good itself, and the Sun,) and that the one reigns over the intelligible world, but the other over the visible, not to say the heavens, lest I should deceive you by the name. You comprehend then, these two orders of things, I mean the visible and the intelligible?—Glauco. I do.—Socrates. Continue this division then, as if it were a line divided into two unequal segments; and each part again, i. e. the sensible and intelligible, divided after a similar manner, and you will have evidence and obscurity placed by each other. In the visible segment, indeed, one part will contain images. But I call images, in the first place, shadows; afterwards, the resemblances of things appearing in water, and in dense, smooth, and lucid bodies, and every thing of this kind, if you apprehend me?—Glauco. I apprehend you.—Socrates. Now conceive that the other section comprehends the things, of which these images are nothing more than similitudes, such as the animals around us, together with plants, and whatever is the work of nature and art.—Glauco. I conceive it.—Socrates. Do you consider this section then, as divided into true and false? And that the hypothesis of opinion is to the knowledge of science, as a resemblance to its original?—Glauco. I do, very readily.—Socrates. Now then, consider how the section of the intelligible is to be divided.—Glauco. How?—Socrates. Thus: one segment is that which the soul enquires after, using the former divisions as images, and compelled to proceed from hypotheses, not to the principle, but to the conclusion. The other is that which employs the cogitative power of the soul, as she proceeds from an hypothesis to a principle no longer supposed, and, neglecting images, advances through their obscurity into the light of ideas themselves.—Glauco. I do not, in this, sufficiently understand you.—Socrates. But again, for you will more easily understand me from what has been already premised. I think you are not ignorant, that those who are conversant in geometry, arithmetic, and the like, suppose even and odd, together with various figures, and the three species of angles, and other things similar to these, according to each method of proceeding. Now, having established these, as hypotheses sufficiently known, they conceive that no reason is to be required for their position: but beginning from these, they descend through the rest, and arrive at last, at the object of their investigation.—Glauco. This I know perfectly well.—Socrates. This also you know, that they use visible forms, and make them the subject of their discourse, at the same time not directing their intellect to the perception of these, but to the originals they resemble; I mean the square itself, and the diameter itself; and not to the figures they delineate. And thus, other forms, which are represented by shadows and images in water, are employed by them, merely as resemblances, while they strive to behold that which can be seen by cogitation alone.—Glauco. You speak the truth.—Socrates. This is what I called above a species of the intelligible, in the investigation of which, the soul was compelled to use hypotheses; not ascending to the principle, as incapable of rising above hypotheses, but using the images formed from inferior objects, to a similitude of such as are superior, and which are so conceived and distinguished by opinion, as if they perspicuously contributed to the knowledge of things themselves.—Glauco. I understand indeed, that you are speaking of the circumstances which take place in geometry, and her kindred arts.—Socrates. Understand now, that by the other section of the intelligible, I mean that which reason herself reaches, by her power of demonstrating, when no longer esteeming hypotheses for principles, but receiving them in reality for hypotheses, she uses them as so many steps and handles in her ascent, until she arrives at that which is no longer hypothetical, the principle of the universe; and afterwards descending, holding by ideas which adhere to the principle, she arrives at the conclusion, employing nothing sensible in her progress, but proceeding through ideas, and in these at last terminating her descent.—Glauco. I understand you, but not so well as I desire: for you seem to me to propose a great undertaking. You endeavour, indeed, to determine that the portion of true being and intelligible, which we speculate by the science of demonstration, is more evident than the discoveries made by the sciences called arts; because in the first hypotheses are principles, and their masters are compelled to employ the eye of cogitation, and not the perceptions of the senses. Yet, because they do not ascend to the principle, but investigate from hypotheses, they seem to you not to have intelligence concerning these, though they are intelligible, through the light of the principle. But you seem to me to call the habit of reasoning on geometrical and the like concerns, cogitation, rather than intelligence, as if cogitation held the middle situation between opinion and intellect.—Socrates. You understand me sufficiently well. And again: with these four proportions take these four corresponding affections of the soul: with the highest intelligence; with the second cogitation; against the third set opinion; and against the fourth assimilation, or imagination. Besides this, establish them in the order of alternate proportion, so that they may partake of evidence, in the same manner as their corresponding objects participate of reality.” I have taken the liberty of translating this fine passage differently from both Petvin and Spens; because they have neglected to give the proper meaning of the word διάνοια, or cogitation, the former translating it mind, and the eye of the mind, and by this means confounding it with intellect; and the latter calling it understanding. But it is certain that Plato, in this place, ranks intellect as the first, on account of the superior evidence of its perceptions; in the next place, cogitation; in the third, opinion; and in the fourth, imagination. However, the reader will please to remember, that by διάνοια, or cogitation, in the present work, is understood that power of the soul which reasons from premises to conclusions, and whose syllogistic energy, on active subjects, is called prudence; and on such as are speculative, science. But for farther information concerning its nature, see the dissertation prefixed to this work, and the following fifth chapter.
[72] These two principles, bound and infinite, will doubtless be considered by the unthinking part of mankind, as nothing more than general terms, and not as the most real of beings. However, an accurate contemplation of the universe, will convince every truly philosophic mind of their reality. For the heavens themselves, by the coherence and order of their parts, evince their participation of bound. But by their prolific powers, and the unceasing revolutions of the orbs they contain, they demonstrate their participation of infinity. And the finite and perpetually abiding forms with which the world is replete, bear a similitude to bound: while, on the contrary, the variety of particulars, their never-ceasing mutation, and the connection of more and less in the communion of forms, represents an image of infinity. Add too, that every natural species, by its form is similar to bound; but by its matter, to infinity. For these two, form and matter, depend on bound and infinity, and are their ultimate progressions. And each of these, indeed, participates of unity; but form is the measure and bound of matter, and is more one. But matter is in capacity all things, because it subsists by an emanation from the first capacity, or the infinite itself.
[73] Of human disciplines, those alone deserve to be called sciences which use no hypotheses, which resolve things into their principles, which are conversant with true being, and elevate us to ideas themselves. Dialectic is wholly of this kind (I mean the dialectic of Plato); for this alone uses no suppositions, but, neglecting shadows and images, raises us, by a sublime investigation, to the principle of the universe; and on this account, deserves to be called the very apex of disciplines. But we must not imagine, that by the word dialectic here, is meant logic, or any part of logic, or that method of disputation, by which we fabricate probable reasons; but we must conceive it as signifying a discipline, endued with the greatest acuteness; neglecting all hypotheses, truly soaring to primary causes, and ultimately reposing in their contemplation. Plotinus has given us most happy specimens of this method, in his books on the genera of being.
[74] See note to the first chapter.
[75] I would particularly recommend this chapter to modern mathematicians, most of whom, I am afraid, have never considered whether or not the subjects of their speculation have any real subsistence: though it is surely an enquiry worthy the earnest attention of every liberal mind. For if the objects of mathematical investigation are merely imaginary, I mean the point without parts, the line without breadth, &c. the science, founded on these false principles, must of course be entirely delusive. Indeed, an absolutely true conclusion, can never flow from an erroneous principle, as from its cause: as the stream must always participate of its source. I mean such a conclusion as is demonstrated by the proper cause, πλὴν οὐ διότι, ἀλλ’ ὅτι, says Aristotle, in his first Analytics; that is, a syllogism from false principles will not prove the why, but only simply that it is: indeed it can only simply prove that it is, to him who admits the false propositions; because he who allows the premises, cannot deny the conclusion, when the syllogism is properly constructed. Thus we way syllogize in the first figure,
And the conclusion will be true, though the major and minor terms are false; but then these terms are not the causes of the conclusion, and we have an inference without a proof. In like manner, if mathematical species are delusive and fictitious, the conclusions deduced from them as principles, are merely hypothetical, and not demonstrative.
[76] Aristotle, in his last Analytics. The reader will please to observe, that the whole force of this nervous, accurate, and elegant reasoning, is directed against Aristotle; who seems unfortunately to have considered, with the moderns, that mathematical species subsist in the soul, by an abstraction from sensibles. See the preceding Dissertation.
[77] Viz. 1, 2, 4, 8, 3, 9, 27. Concerning which, see lib. iii. of Proclus’s excellent Commentary on the Timæus.
[78] Plato frequently, both in the Meno and elsewhere, shews that science is Reminiscence; and I think not without the strongest reason. For since the soul is immaterial, as we have demonstrated in the dissertation to this work, she must be truly immortal, i. e. both a parte ante, & a parte post. That she must be eternal, indeed, with respect to futurity, if immaterial, is admitted by all; and we may prove, with Aristotle, in his first book de Cœlo, that she is immortal, likewise a parte ante, as follows. Every thing without generation, is incorruptible, and every thing incorruptible, is without generation: for that which is without generation, has a necessity of existing infinitely a parte ante (from the hypothesis); and therefore, if it possesses a capacity of being destroyed, since there is no greater reason why it should be corrupted now, rather than in some former period, it is endued with a capacity of being destroyed and ceasing to be, in every instant of infinite time, in which it necessarily is. In like manner, that which is incorruptible, has a necessity of existing infinitely a parte post; therefore, if it possesses a capacity of being generated, since there is no greater reason why it should be generated now rather than afterwards, it possesses a capacity of being generated, in every instant of time, in which it necessarily is. If then the soul is essentially immortal, with respect to the past and future circulations of time; and if she is replete with forms or ideas of every kind, as we have proved in the dissertation, she must, from her circulating nature, have been for ever conversant in alternately possessing and losing the knowledge of these. Now, the recovery of this knowledge by science, is called by Plato, reminiscence; and is nothing more than a renewed contemplation of those divine forms, so familiar to the soul, before she became involved in the dark vestment of an earthly body. So that we may say, with the elegant Maximus Tyrus, (Disser. 28.) “Reminiscence is similar to that which happens to the corporeal eye, which, though always endued with a power of vision, yet darkness sometimes obstructs its passage, and averts it from the perception of things. Art therefore, approaches, which though it does not give to the eye the power of vision, yet removes its impediments, and affords a free egress to its rays. Conceive now, that our rational soul is such a power of perceiving, which sees and knows the nature of beings. To this the common calamity of bodies happens, that darkness spreading round it, hurries away its aspect, blunts its sharpness, and extinguishes its proper light. Afterwards, the art of reason approaches, which, like a physician, does not bring or afford it a new science, but rouses that which it possesses, though very slender, confused, and unsteady.” Hence, since the soul, by her immersion in body, is in a dormant state, until she is roused by science to an exertion of her latent energies; and yet even previous to this awakening, since she contains the vivid sparks, as it were, of all knowledge, which only require to be ventilated by the wings of learning, in order to rekindle the light of ideas, she may be said in this case to know all things as in a dream, and to be ignorant of them with respect to vigilant perceptions. Hence too, we may infer that time does not antecede our essential knowledge of forms, because we possess it from eternity: but it precedes our knowledge with respect to a production of these reasons into perfect energy. I only add, that I would recommend the liberal English reader, to Mr. Sydenham’s excellent translation of Plato’s Meno, where he will find a familiar and elegant demonstration of the doctrine of Reminiscence.
[79] Concerning this valuable work, entitled ΙΕΡΟ‘Σ ΛΟΓΟ’Σ, see the Bibliotheca Græca of Fabricius, vol. i. p. 118 and 462, and in the commentary of Syrianus on Aristotle’s metaphysics, p. 7, 71, 83, and 108, the reader will find some curious extracts from this celebrated discourse; particularly in p. 83. Syrianus informs us, “that he who consults this work will find all the orders both of Monads and Numbers, without neglecting one, fully celebrated (ὐμνουμένας.)” There is no doubt, but that Pythagoras and his disciples concealed the sublimest truths, under the symbols of numbers; of which he who reads and understands the writings of the Platonists will be fully convinced. Hence Proclus, in the third book of his excellent commentary on the Timæus, observes, “that Plato employed mathematical terms for the sake of mystery and concealment, as certain veils, by which the penetralia of truth might be secluded from vulgar inspection, just as the theologists made fables, but the Pythagoreans symbols, subservient to the same purpose: for in images we may speculate their exemplars, and the former afford us the means of access to the latter.”
[80] Concerning this Geometric Number, in the 8th book of Plato’s Republic, than which Cicero affirms there is nothing more obscure, see the notes of Bullialdus to Theo. p. 292.
[81] I am sorry to say, that this part of the enemies to pure geometry and arithmetic, are at the present time very numerous; conceptions of utility in these sciences, extending no farther than the sordid purposes of a mere animal life. But surely, if intellect is a part of our composition, and the noblest part too, there must be an object of its contemplation; and this, which is no other than truth in the most exalted sense, must be the most noble and useful subject of speculation to every rational being.
[82] In the 13th book of his Metaphysics, cap. iii.
[83] In. I. De Partib. Animalium, et in primo Ethic. cap. iii.
[84] See more concerning this in the Dissertation.
[85] Since number is prior to magnitude, the demonstrations of arithmetic must be more intellectual, but those of geometry more accommodated to the rational power. And when either arithmetic or geometry is applied to sensible concerns, the demonstrations, from the nature of the subjects, must participate of the obscurity of opinion. If this is the case, a true mathematician will value those parts of his science most, which participate most of evidence; and will consider them as degraded, when applied to the common purposes of life.
[86] This division of the mathematical science, according to the Pythagoreans, which is nearly coincident with that of Plato, is blamed by Dr. Barrow in his Mathematical Lectures, p. 15. as being confined within too narrow limits: and the reason he assigns for so partial a division, is, “because, in Plato’s time, others were either not yet invented, or not sufficiently cultivated, or at least were not yet received into the number of the mathematical sciences.” But I must beg leave to differ from this most illustrious mathematician in this affair; and to assert that the reason of so confined a distribution (as it is conceived by the moderns) arose from the exalted conceptions these wise men entertained of the mathematical sciences, which they considered as so many preludes to the knowledge of divinity, when properly pursued; but they reckoned them degraded and perverted, when they became mixed with sensible objects, and were applied to the common purposes of life.
[87] That is, a right and circular line.
[88] I am afraid there are few in the present day, who do not consider tactics as one of the most principal parts of mathematics; and who would not fail to cite, in defence of their opinions, that great reformer of philosophy, as he is called, Lord Bacon, commending pursuits which come home to men’s businesses and bosoms. Indeed, if what is lowest in the true order of things, and best administers to the vilest part of human nature, is to have the preference, their opinion is right, and Lord Bacon is a philosopher!
[89] By this is to be understood the art new called Perspective: from whence it is evident that this art was not unknown to the ancients, though it is questioned by the moderns.
[90] From hence it appears, that it is doubtful whether Plato is the author of the dialogue called Epinomis; and I think it may with great propriety be questioned. For though it bears evident marks of high antiquity, and is replete with genuine wisdom, it does not seem to be perfectly after Plato’s manner; nor to contain that great depth of thought with which the writings of this philosopher abound. Fabricius (in his Bibliotheca Græca, lib. i. p. 27.) wonders that Suidas should ascribe this work to a philosopher who distributed Plato’s laws into twelve books, because it was an usual opinion; from whence it seems, that accurate critic had not attended to the present passage.
[91] This proximate conjunction of the mathematical sciences, which Proclus considers as subordinate to dialectic, seems to differ from that vertex of science in this, that the former merely embraces the principles of all science, but the latter comprehends the universal genera of being, and speculates the principle of all.
[92] In the Meno.
[93] This is certainly the true or philosophical employment of the mathematical science; for by this means we shall be enabled to ascend from sense to intellect, and rekindle in the soul that divine light of truth, which, previous to such an energy, was buried in the obscurity of a corporeal nature. But by a contrary process, I mean, by applying mathematical speculations, to experimental purposes, we shall blind the liberal eye of the soul, and leave nothing in its stead but the darkness of corporeal vision, and the phantoms of a degraded imagination.
[94] The design of the present chapter is to prove that the figures which are the subjects of geometric speculation, do not subsist in external and sensible matter, but in the receptacle of imagination, or the matter of the phantasy. And this our philosopher proves with his usual elegance, subtilty, and depth. Indeed, it must be evident to every attentive observer, that sensible figures fall far short of that accuracy and perfection which are required in geometrical definitions: for there is no sensible circle perfectly round, since the point from which it is described is not without parts; and, as Vossius well observes, (de Mathem. p. 4.) there is not any sphere in the nature of things, that only touches in a point, for with some part of its superficies it always touches the subjected plane in a line, as Aristotle shews Protagoras to have objected against the geometricians. Nor must we say, with that great mathematician Dr. Barrow, in his Mathematical Lectures, page 76, “that all imaginable geometrical figures, are really inherent in every particle of matter, in the utmost perfection, though not apparent to sense; just as the effigies of Cæsar lies hid in the unhewn marble, and is no new thing made by the statuary, but only is discovered and brought to sight by his workmanship, i. e. by removing the parts of matter by which it is overshadowed and involved. Which made Michael Angelus, the most famous carver, say, that sculpture was nothing but a purgation from things superfluous. For take all that is superfluous, (says he) from the wood or stone, and the rest will be the figure you intend. So, if the hand of an angel (at least the power of God) should think fit to polish any particle of matter, without vacuity, a spherical superficies would appear to the eyes, of a figure exactly round; not as created anew, but as unveiled and laid open from the disguises and covers of its circumjacent matter.” For this would be giving a perfection to sensible matter, which it is naturally incapable of receiving: since external body is essentially full of pores and irregularities, which must eternally prevent its receiving the accuracy of geometrical body, though polished by the hand of an angel. Besides, what polishing would ever produce a point without parts, and a line without breadth? For though body may be reduced to the greatest exility, it will not by this means ever pass into an incorporeal nature, and desert its triple dimension. Since external matter, therefore, is by no means the receptacle of geometrical figures, they must necessarily reside in the catoptric matter of the phantasy, where they subsist with an accuracy sufficient for the energies of this science. It is true, indeed, that even in the purer matter of imagination, the point does not appear perfectly impartible, nor the line without latitude: but then the magnitude of the point, and the breadth of the line is indefinite, and they are, at the same time, unattended with the qualities of body, and exhibit to the eye of thought, magnitude alone. Hence, the figures in the phantasy, are the proper recipients of that universal, which is the object of geometrical speculation, and represent, as in a mirror, the participated subsistence of those vital and immaterial forms which essentially reside in the soul.
[95] This division is elegantly explained by Ammonius, (in Porphyr. p. 12.) as follows, “Conceive a seal-ring, which has the image of some particular person, for instance, of Achilles, engraved in its seal, and let there be many portions of wax, which are impressed by the ring. Afterwards conceive that some one approaches, and perceives all the portions of wax, stamped with the impression of this one ring, and keeps the impression of the ring in his mind: the seal engraved in the ring, represents the universal, prior to the many: the impression in the portions of wax, the universal in the many: but that which remains in the intelligence of the beholder, may be called the universal, after and posterior to the many. The same must we conceive in genera and species. For that best and most excellent artificer of the world, possesses within himself the forms and exemplars of all things: so that in the fabrication of man, he looks back upon the form of man resident in his essence, and fashions all the rest according to its exemplar. But if any one should oppose this doctrine, and assert that the forms of things do not reside with their artificer, let him attend to the following arguments. The artificer either knows, or is ignorant of that which he produces: but he who is ignorant will never produce any thing. For who will attempt to do that, which he is ignorant how to perform? since he cannot act from an irrational power like nature, whose operations are not attended with animadversion. But if he produces any thing by a certain reason, he must possess a knowledge of every thing which he produces. If, therefore, it is not impious to assert, that the operations of the Deity, like those of men, are attended with knowledge, it is evident that the forms of things must reside in his essence: but forms are in the demiurgus, like the seal in the ring; and these forms are said to be prior to the many, and separated from matter. But the species man, is contained in each particular man, like the impression of the seal in the wax, and is said to subsist in the many, without a separation from matter. And when we behold particular men, and perceive the same form and effigy in each, that form seared in our soul, is said to be after the many, and to have a posterior generation: just as we observed in him, who beheld many seals impressed in the wax from one and the same ring. And this one, posterior to the many, may be separated from body, when it is conceived as not inherent in body, but in the soul: but is incapable of a real separation from its subject.” We must here, however, observe, that when Ammonius speaks of the knowledge of the Deity, it must be conceived as far superior to ours. For he possesses a nature more true than all essence, and a perception clearer than all knowledge. And as he produced all things by his unity, so by an ineffable unity of apprehension, he knows the universality of things.
[96] In lib. vii. Metaphys. 35 & 39.
[97] In lib. iii. de Anima, tex. 20.
[98] That is, geometry first speculates the circle delineated on paper, or in the dust: but by the medium of the circular figure in the phantasy, contemplates the circle resident in cogitation; and by that universal, or circular reason, participated in the circle of the phantasy, frames its demonstrations.
[99] In his first Analytics, t. 42. See the Dissertation to this work.
[100] Such as the proportion of the diagonal of a square to its side; and that of the diameter of a circle, to the periphery.
[101] The gnomons, from which square numbers are produced, are odd numbers in a natural series from unity, i. e. 1, 3, 5, 7, 9, 11, &c. for these, added to each other continually, produce square numbers ad infinitum. But these gnomons continually decrease from the highest, and are at length terminated by indivisible unity.
[102] This doctrine of ineffable quantities, or such whose proportion cannot be expressed, is largely and accurately discussed by Euclid, in the tenth book of his Elements: but its study is neglected by modern mathematicians, because it is of no use, that is, because it contributes to nothing mechanical.
[103] This proposition is the 11th of the second book: at
least, the method of dividing a line into extreme and mean proportion,
is immediately deduced from it; which is done by Euclid, in the 30th,
of the sixth book. Thus, Euclid shews (11. 2.) how to divide the line
(A G B) A B, so that the rectangle under the whole A B, and
the segment G B, may be equal to the square made from A G: for when
this is done, it follows, that as A B is to A G, so is A G to G B; as
is well known. But this proposition, as Dr. Barrow observes, cannot be
explained by numbers; because there is not any number which can be so
divided, that the product from the whole into one part, may be equal to
the square from the other part.
A B, so that the rectangle under the whole A B, and
the segment G B, may be equal to the square made from A G: for when
this is done, it follows, that as A B is to A G, so is A G to G B; as
is well known. But this proposition, as Dr. Barrow observes, cannot be
explained by numbers; because there is not any number which can be so
divided, that the product from the whole into one part, may be equal to
the square from the other part.
[104] All polygonous figures, may, it is well known, be resolved into triangles; and this is no less true of polygonous numbers, as the following observations evince. All number originates from indivisible unity, which corresponds to a point: and it is either linear, corresponding to a line; or superficial, which corresponds to a superficies; or solid, which imitates a geometrical solid. After unity, therefore, the first of linear numbers is the duad; just as every finite line is allotted two extremities. The triad is the first of superficial numbers; as the triangle of geometrical figures. And the tetrad, is the first of solids; because a triangular pyramid, is the first among solid numbers, as well as among solid figures. As, therefore, the monad is assimilated to the point, so the duad to the line, the triad to the superficies, and the tetrad to the solid. Now, of superficial numbers, some are triangles, others squares, others pentagons, hexagons, heptagons, &c. Triangular numbers are generated from the continual addition of numbers in a natural series, beginning from unity. Thus, if the numbers 1, 2, 3, 4, 5, &c. be added to each other continually, they will produce the triangular numbers 1, 3, 6, 10, 15, &c. and if every triangular number be added to its preceding number, it will produce a square number. Thus 3 added to 1 makes 4; 6 added to 3 is equals 9; 10 added to 6 is equal to 16; and so of the rest. Pentagons, are produced from the junction of triangular and square numbers, as follows. Let there be a series of triangular numbers 1, 3, 6, 10, 15, &c.
And of squares 1, 4, 9, 16, 25, &c.
Then the second square number, added to the first triangle, will produce the first pentagon from unity, i.e. 5. The third square added to the second triangle, will produce the second pentagon, i.e. 12; and so of the rest, by a similar addition. In like manner, the second pentagon, added to the first triangle, will form the first hexagon from unity; the third pentagon and the second triangle, will form the second hexagon, &c. And, by a similar proceeding, all the other polygons may be obtained.
[105] Intellections are universally correspondent to their objects, and participate of evidence or the contrary, in proportion as their subjects are lucid or obscure. Hence, Porphyry, in his sentences, justly observes, that “we do not understand in a similar manner with all the powers of the soul, but according to the particular essence of each. For with the intellect we understand intellectually; and with the soul, rationally: our knowledge of plants is according to a seminal conception; our understanding of bodies is imaginative; and our intellection of the divinely solitary principle of the universe, who is above all things, is in a manner superior to intellectual perception, and by a super-essential energy.” Ἀφορμαὶ πρὸς τὰ Νοητὰ, (10.) So that, in consequence of this reasoning, the speculations of geometry are then most true, when most abstracted from sensible and material natures.
[106] See Plutarch, in the life of Marcellus.
[107] In lib. i. de Cælo, tex. 22. et lib. i. Meteo. cap. 3. Aristotle was called demoniacal by the Platonic philosophers, in consequence of the encomium bestowed on him by his master, Plato, “That he was the dæmon of nature.” Indeed, his great knowledge in things subject to the dominion of nature, well deserved this encomium; and the epithet divine, has been universally ascribed to Plato, from his profound knowledge of the intelligible world.
[108] Εἰς νοῦν, is wanting in the original, but is supplied by the excellent translation of Barocius.
[109] Ἀλόγων, in the printed Greek, which Fabricius, in his Bibliotheca Græca, vol. i. page 385, is of opinion, should be read ἀναλόγων; but I have rendered the word according to the translation of Barocius, who is likely to have obtained the true reading, from the variety of manuscripts which he consulted.
[110] The quadrature of the Lunula is as follows.
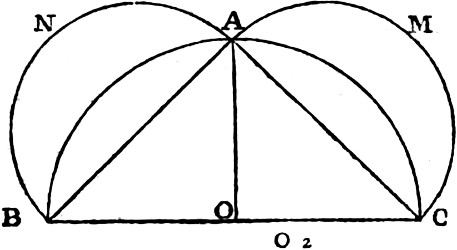
Let A B C be a right-angled triangle, and B A C a semi-circle on the diameter B C: B N A a semi-circle described on the diameter A B; A M C a semi-circle described on the diameter A C. Then the semi-circle B A C is equal to the semi-circle B N A, and A M C together: (because circles are to each other as the squares of their diameters, 31, 6.) If, therefore, you take away the two spaces B A, A C common on both sides, there will remain the two lunulas B N A, A M C, bounded on both sides with circular lines, equal to the right-angled triangle B A C. And if the line B A, be equal to the line A C, and you let fall a perpendicular to the hypotenuse B C, the triangle B A O will be equal to the lunular space B N A, and the triangle C O A will be equal to the lunula C M A. Those who are curious, may see a long account of an attempt of Hippocrates to square the circle, by the invention of the lunulas, in Simplicius on Aristotle’s Physics, lib. i.
[111] So Barocius reads, but Fabricius Μεδμᾶιος.
[112] i. e. The five regular bodies, the pyramid, cube, octaedron, dodecaedron and icosaedron; concerning which, and their application to the theory of the universe, see Kepler’s admirable work, De Harmonia Mundi.
[113] It may be doubted whether the optics and catoptrics, ascribed to Euclid in the editions of his works are genuine: for Savil, and Dr. Gregory, think them scarcely worthy so great a man.
[114] There are two excellent editions of this work, one by Meibomius, in his collection of ancient authors on harmony; and the other by Dr. Gregory, in his collection of Euclid’s works.
[115] This work is most probably lost. See Dr. Gregory’s Euclid.
[116] All this is shewn by Proclus in the following Commentaries; and is surely most admirable and worthy the investigation of every liberal mind; but I am afraid modern mathematicians very little regard such knowledge, because it cannot be applied to practical and mechanical purposes.
[117] This work is unfortunately lost.
[118] Because this is true only in isosceles and equilateral triangles.
[119] This follows from the 32d proposition of the first book of Euclid; and is demonstrated by Dr. Barrow, in his scholium to that proposition.
[120] The method of constructing these is shewn by our philosopher, in his comment on the first proposition, as will appear in the second volume of this work.
[121] The reader will please to observe, that the definitions are, indeed, hypotheses, according to the doctrine of Plato, as may be seen in the note to chap, i. book I. of this work.
[122] In his last Analytics. See the preceding Dissertation.
[123] That part of this work enclosed within the brackets, is wanting in the original; which I have restored from the excellent version of Barocius. The philosophical reader, therefore, of the original, who may not have Barocius in his possession, will, I hope, be pleased, to see so great a vacancy supplied; especially, as it contains the beginning of the commentary on the definition of a point.
[124] I do not find this ænigma among the Pythagoric symbols which are extant; so that it is probably no where mentioned but in the present work. And I am sorry to add, that a figure and three oboli, in too much the general cry of the present times.
[125] The present Comment, and indeed most of the following, eminently evinces the truth of Kepler’s observation, in his excellent work, De Harmonia Mundi, p. 118. For, speaking of our author’s composition in the present work, which he every where admires and defends, he remarks as follows, “oratio fluit ipsi torrentis instar, ripas inundans, et cæca dubitationum vada gurgitesque occultans, dum mens plena majestatis tantarum rerum, luctatur in angustiis linguæ, et conclusio nunquam sibi ipsi verborum copiâ satisfaciens, propositionum simplicitatem excedit.” But Kepler was skilled in the Platonic philosophy, and appears to have been no less acquainted with the great depth of our author’s mind than with the magnificence and sublimity of his language. Perhaps Kepler is the only instance among the moderns, of the philosophical and mathematical genius being united in the same person.
[126] That is, the reason of a triangular figure (for instance) in the phantasy, or triangle itself, is superior to the triangular nature participated in that figure.
[127] In the tenth book of his Republic.
[128] See the Hymn to the Mother of the Gods, in my translation of the Orphic Initiations.
[129] The philosopher here seems to contradict what he asserts in the end of his comment on the 13th Definition: for there he asserts, that the circle is a certain plane space. Perhaps he may be reconciled, by considering, that as the circle subsists most according to bound, when we speculate its essence in this respect we may define it according to the circumference, which is the cause of its bound. But when we consider it as participating of infinity also, though not in so eminent a degree, and view it from its emanations from the centre as well as in its regressions, we may define it a plane space.
[130] That is, the essential one of the soul is the mother of number; but that which subsists in opinion is nothing more than the receptacle of the former; just as matter is the seat of all forms. For a farther account of the subsistence of numbers, see the first section of the preceding Dissertation.
[131] That is, number composed from units.
[132] This sentence within the brackets, is wholly omitted in the printed Greek.
[133] In i. De Cælo.
[134] This sentence within the brackets, which is very imperfect in the Greek, I have supplied from the excellent translation of Barocius. In the Greek there is nothing more than λὲγω δὲ ἑνὸν τῂν γραμμὴν δυαδός πρὸς τὸ στερεόν.
[135] In the Greek, γὰρ ἡ μονὰς ἐκεῖ πρῶτον, ὅπου πατρικὴ μονάς ἐστι φησὶ τὸ λόγιον. The latter part only of this oracle, is to be found in all the printed editions of the Zoroastrian oracles; though it is wonderful how this omission could escape the notice of so may able critics, and learned men. It seems probable, from hence, that it is only to be found perfect in the present work.
[136] The word τανάη, is omitted in the Greek.
[137] This and the following problems, are the 1st, 22d, and 12th propositions of the first book. But in the two last, instead of the word ἄπειρος or infinite, which is the term employed by Euclid, Mr. Simson, in his edition of the Elements, uses the word unlimited. But it is no unusual thing with this great geometrician, to alter the words of Euclid, when they convey a philosophical meaning; as we shall plainly evince in the course of these Commentaries. He certainly deserves the greatest praise for his zealous attachment to the ancient geometry: but he would (in my opinion) have deserved still more, had he been acquainted with the Greek philosophy; and fathomed the depth of Proclus; for then he would never have attempted to restore Euclid’s Elements, by depriving them of some very considerable beauties.
[138] This is doubtless the reason why the proportion between a right and circular line, cannot be exactly obtained in numbers; for on this hypothesis, they must be incommensurable quantities; because the one contains property essentially different from the other.
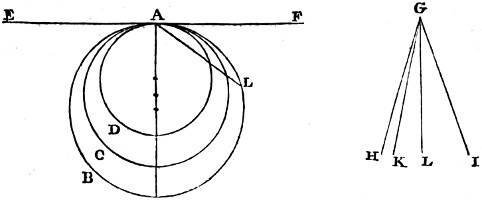
The cornicular angle is that which is made from the periphery of a circle and its tangent; that is, the angle comprehended by the arch L A, and the right line F A, which Euclid in (16. 3.) proves to be less than any right-lined angle. And from this admirable proposition it follows, by a legitimate consequence, that any quantity may be continually and infinitely increased, but another infinitely diminished; and yet the augment of the first, how great soever it may be, shall always be less than the decrement of the second: which Cardan demonstrates as follows. Let there be proposed an angle of contact B A E, and an acute angle H G I. Now if there be other lesser circles described A C, A D, the angle of contact will be evidently increased. And if between the right lines G H, G I, there fall other right lines G K, G L, the acute angle shall be continually diminished: yet the angle of contact, however increased, is always less than the acute angle, however diminished. Sir Isaac Newton likewise observes, in his Treatise on Fluxions, that there are angles of contact made by other curve lines, and their tangents infinitely less than those made by a circle and right line; all which is demonstrably certain: yet, such is the force of prejudice, that Mr. Simson is of opinion, with Vieta, that this part of the 16th proposition is adulterated; and that the space made by a circular line and its tangent, is no angle. At least his words, in the note upon this proposition, will bear such a construction. Peletarius was likewise of the same opinion; but is elaborately confuted by the excellent Clavius, as may be seen in his comment on this proposition. But all the difficulties and paradoxes in this affair, may be easily solved and admitted, if we consider, with our philosopher, that the essence of an angle does not subsist in ether quantity, quality, or inclination, taken singly, but in the aggregate of them all. For if we regard the inclination of a circular line to its tangent, we shall find it possess the property, by which Euclid defines an angle: if we respect its participation of quantity, we shall find it capable of being augmented and diminished; and if we regard it as possessing a peculiar quality, we shall account for its being incommensurable with every right-lined angle. See the Comment on the 8th Definition.
[140] In i. De Cælo.
[141] It is from this cylindric spiral that the screw is formed.
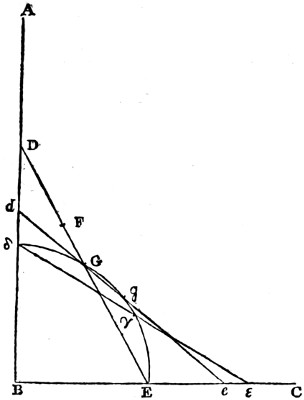
The present very obscure passage, may be explained by the following figure. Let A B C, be a right angle, and D E the line to be moved, which is bisected in G. Now, conceive it to be moved along the lines A B, B C, in such a manner, that the point D may always remain in A B, and the point E in B C. Then, when the line D E, is in the situations d e, δ ε, the point G, shall be in g, γ, and these points G, g, γ, shall be in a circle. And any other point F in the line D E, will, at the same time, describe an ellipsis; the greater axis being in the line A B, when the point F is between D and G; and in the line B C, when the point F is between G and E.
[143] That is, the soul of the world.
[144] In Timæo.
[145] The ellipsis.
[146] The cissoid. For the properties of this curve, see Dr. Wallis’s treatise on the cycloid, p. 81.
[147] The conchoid.
[148] Thus, a right line, when considered as the side of a parallelogram, moving circularly, generates a cylindrical superficies: when moving circularly, as the side of a triangle, a conical surface; and so in other lines, the produced superficies varying according to the different positions of their generative lines.
[149] Inv ii. De Rep.
[150] In multis locis.
[151] This definition is the same with that which Mr. Simson has adopted instead of Euclid’s, expressed in different words: for he says, “a plane superficies is that in which any two points being taken, the straight line between them lies wholly in that superficies.” But he does not mention to whom he was indebted for the definition; and this, doubtless, because he considered it was not worth while to relate the trifles of Proclus at full length: for these are his own words, in his note to proposition 7, book i. Nor has he informed us in what respect Euclid’s definition is indistinct.
[152] In the Greek ἐννοιὰς, but it should doubtless be read εἰκόνας, images, as in the translation of Barocius.
[153] Mr. Simson, in his note on this definition, supposes it to be the addition of some less skilful editor; on which account, and because it is quite useless (in his opinion) he distinguishes it from the rest by inverted double commas. But it is surely strange that the definition of angle in general should be accounted useless, and the work of an unskilful geometrician. Such an assertion may, indeed, be very suitable to a professor of experimental philosophy, who considers the useful as inseparable from practice; but is by no means becoming a restorer of the liberal geometry of the ancients. Besides, Mr. Simson seems continually to forget that Euclid was of the Platonic sect; and consequently was a philosopher as well as a mathematician. I only add, that the commentary on the present definition is, in my opinion, remarkably subtle and accurate, and well deserves the profound attention of the greatest geometricians.
[154] For a philosophical discussion of the nature of quality and quantity, consult the Commentaries of Ammonius, and Simplicius on Aristotle’s Categories, Plotinus on the genera of beings, and Mr. Harris’s Philosophical Arrangements.
[155] That is, the ellipsis.
[156] That is, they are either right, acute, or obtuse.
[157] This oracle is not mentioned by any of the collectors of the Zoroastrian oracles.
[158] This, indeed, must always be the case with those geometricians, who are not at the same time, philosophers; a conjunction no less valuable than rare. Hence, from their ignorance of principles and intellectual concerns, when any contemplative enquiry is proposed, they immediately ask, in what its utility consists; considering every thing as superfluous, which does not contribute to the solution of some practical problem.
[159] Concerning the soul’s descent into body, see lib. ix., Ennead iv. of Plotinus; and for the method by which she may again return to her pristine felicity, study the first book of Porphyry’s Treatise on Abstinence.
[160] This Definition too, is marked by Mr. Simson with inverted commas, as a symbol of its being interpolated. But for what reason I know not, unless because it is useless, that is, because it is philosophical!
[161] That is, the various species of forms, with which the four elements are replete.
[162] That is, the circle.
[163] An admirer of the moderns, and their pursuits, will doubtless consider all this as the relics of heathen superstition and ignorance; and will think, perhaps, he makes a great concession in admitting the existence of one supreme god, without acknowledging a multitude of deities subordinate to the first. For what the ancients can urge in defence of this obsolete opinion, I must beg leave to refer the reader to the dissertation prefixed to my translation of Orpheus; in addition to which let him attend to the following considerations. Is it possible that the machinery of the gods in Homer could be so beautiful, if such beings had no existence? Or can any thing be beautiful which is destitute of all reality? Do not things universally please in proportion as they resemble reality? Perhaps it will be answered, that the reverse of this is true, and that fiction more generally pleases than truth, as is evident from the great avidity with which romances are perused. To this I reply, that fiction itself ceases to be pleasing, when it supposes absolute impossibilities: for the existence of genii and fairies cannot be proved impossible; and these compose all the marvellous of romance. This observation is verified in Spencer’s Fairy Queen: for his allegories, in which the passions are personified, are tedious and unpleasant, because they are not disguised under the appearance of reality: while the magic of Circe, the bower of Calypso, the rocks of Scylla and Charybdis, and the melody of the Syrens, in the Odyssey of Homer, though nothing but allegories, universally enchant and delight, because they are covered with the semblance of truth. It is on this account that Mikon’s battles in heaven are barbarous and ridiculous in the extreme; for every one sees the impossibility of supposing gun-powder and cannons in the celestial regions: the machinery is forced and unnatural, contains no elegance of fancy, and is not replete with any mystical information. On the contrary, Homer’s machinery is natural and possible, is full of dignity and elegance, and is pregnant with the sublimest truths; it delights and enobles the mind of the reader, astonishes him with its magnificence and propriety, and animates him with the fury of poetic inspiration. And this, because it is possible and true.
[164] The sentence within the brackets is omitted in the Greek.
[165] That is, the circular form proceeds from bound, but right-lined figures from infinity.
[166] That is, the number three.
[167] In Timæo.
[168] πρὸς ὃ, or, to which, is wanting in the original, and in all the published collections of the Zoroastrian oracles.
[169] That is Jupiter, who is called triadic, because he proceeds from Saturn and Rhea; and because his government is participated by Neptune and Pluto, for each of these is called Jupiter by Orpheus.
[170] This sentence, within the brackets, is omitted in the printed Greek.
Fig. I. Fig. II.
Thus let a part A E B cut off by the diameter A B (fig. I.) of the circle A E B D be placed on the other part A D B, as in fig. II. Then, if it is not equal to the other part, either A E B will fall within A D B, or A D B within A E B: but in either case, C E will be equal to C D, which is absurd.
[172] This objection is urged by Philoponus, in his book against Proclus on the eternity of the world; but not, in my opinion, with any success. See also Simplicius, in his third digression against Philoponus, in his commentary on the 8th book of Aristotle’s Physics.
[173] This definition is no where extant but in the commentaries of Proclus. Instead of it, in almost all the printed editions of Euclid, the following is substituted. A segment of a circle is the figure contained by a diameter, and the part of the circumference cut off by the diameter. This Mr. Simson has marked with commas, as a symbol of its being interpolated: but he has taken no notice of the different reading in the commentaries of Proclus. And what is still more remarkable, this variation is not noticed by any editor of Euclid’s Elements, either ancient or modern.
[174] As in every hyperbola.
[175] The Platonic reader must doubtless be pleased to find that Euclid was deeply skilled in the philosophy of Plato, as Proclus every where evinces. Indeed, the great accuracy, and elegant distribution of these Elements, sufficiently prove the truth of this assertion. And it is no inconsiderable testimony in favour of the Platonic philosophy, that its assistance enabled Euclid to produce such an admirable work.
[176] Concerning these crowns, or annular spaces, consult the great work of that very subtle and elegant mathematician Tacquet, entitled Cylindrica et Annularia.
[177] In the preceding tenth commentary.
[178] This in consequence of every triangle possessing angles alone equal to two right.
[179] This too, follows from the same cause as above.
[180] Thus the following figure A B D C has four sides, and but three angles.
[181] The Greek in this place is very erroneous, which I have restored from the version of Barocius.
[182] For the Greek word ῥόμβος is derived from the verb ῥέμβω, which signifies to have a circumvolute motion.
[183] See the Orphic Hymns of Onomacritus to these deities; my translation of which I must recommend to the English reader, because there is no other.
[184] These twelve divinities, of which Jupiter is the head, are, Jupiter, Neptune, Vulcan, Vesta, Minerva, Mars, Ceres, Juno, Diana, Mercury, Venus, and Apollo. The first triad of these is demiurgic, the second comprehends guardian deities, the third is vivific, or zoogonic, and the fourth contains elevating gods. But, for a particular theological account of these divinities, study Proclus on Plato’s Theology, and you will find their nature unfolded, in page 403, of that admirable work.
[185] For it is easy to conceive a cylindric spiral described about a right-line, so as to preserve an equal distance from it in every part; and in this case the spiral and right-line will never coincide though infinitely produced.
As the conchoid is a curve but little known, I have subjoined the following account of its generation and principal property. In any given right line A P, call P the pole, A the vertex, and any intermediate point C the centre of the conchoid: likewise, conceive an infinite right line C H, which is called a rule, perpendicular to A P. Then, if the right line A p continued at p as much as is necessary, is conceived to be so turned about the abiding pole p, that the point C may perpetually remain in the right line C H, the point A will describe the curve A o, which the ancients called a conchoid.
In this curve it is manifest (on account of the right line P O, cutting the rule in H that the point o will never arrive at rule C H; but because h O is perpetually equal to C A, and the angle of section is continually more acute, the distance of the point O from C H will at length be less than any given distance, and consequently the right line C H will be an asymptote to the curve A O.
When the pole is at P, so that P C is equal to C A, the conchoid A O described by the revolution of P A, is called a primary conchoid, and those described from the poles p, and π, or the curves A o, A ω, secondary conchoids; and these are either contracted or protracted, as the eccentricity P C, is greater or less than the generative radius C A, which is called the altitude of the curve.
Now, from the nature of the conchoid, it may be easily inferred, that not only the exterior conchoid A ω will never coincide with the right line C H, but this is likewise true of the conchoids A O, A o; and by infinitely extending the right-line A π, an infinite number of conchoids may be described between the exterior conchoid A ω, and the line C H, no one of which shall ever coincide with the asymptote C H. And this paradoxical property of the conchoid which has not been observed by any mathematician, is a legitimate consequence of the infinite divisibility of quantity. Not, indeed, that quantity admits of an actual division in infinitum, for this is absurd and impossible; but it is endued with an unwearied capacity of division, and a power of being diffused into multitude, which can never be exhausted. And this infinite capacity which it possesses arises from its participation of the indefinite duad; the source of boundless diffusion, and innumerable multitude.
But this singular property is not confined to the conchoid, but is found in the following curve. Conceive that the right line A C which is perpendicular to the indefinite line X Y, is equal to the quadrantal arch H D, described from the centre C, with the radius C D: then from the same centre C, with the several distances C E, C F, C G, describe the arches E l, F n, G p, each of which must be conceived equal to the first arch H D, and so on infinitely. Now, if the points H, k, l, n, p, be joined, they will form a curve line, approaching continually nearer to the right-line A B (parallel to C Y) but never effecting a perfect coincidence. This will be evident from considering that each of the sines of the arches H D, l E, n F, &c. being less than its respective arch, must also be less than the right-line A C, and consequently can never coincide with the right-line A B.
But if other arches D i, E m, F o, &c. each of them equal to the right-line A C, and described from one centre, tangents to the former arches H D, l E, n F, &c. be supposed; it is evident that the points H, i, m, o, &c. being joined, will form a curve line, which shall pass beyond the former curve, and converge still nearer to the line A B, without a possibility of ever becoming coincident: for since the arches D i, E m, F o, &c. have less curvature than the former arches, but are equal to them in length, it is evident that they will be subtended by longer lines, and yet can never touch the right-line A B. In like manner, if other tangent arches be drawn to the former, and so on infinitely, with the same conditions, an infinite number of curve-lines will be formed, each of them passing between H p and A B, and continually diverging from the latter, without a possibility of ever coinciding with the former. This curve, which I invented some years since, I suspect to be a parabola; but I have not yet had opportunity to determine it with certainty.
Transcriber’s Notes:
1. Obvious printers’, punctuation and spelling errors have been
corrected silently.
2. Where hyphenation is in doubt, it has been retained as in the
original.
3. Some hyphenated and non-hyphenated versions of the same words have
been retained as in the original.
4. The errata have been soilently corrected.